| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-6 5:34 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【40】RC並列回路とひずみ波電流 今度はRC並列回路とひずみ波の問題。
図のような回路で、基本波と高調波の電流の最大値の比を求めよというもの。 ひずみ波電圧は e=E*(sin(ωt)+h*sin(3ωt)) で与えられる。 これも線形回路の重ね合わせで解くことができる。 基本波と高調波に関する負荷インピーダンスはそれぞれ Z1=1/(1/R+jωC) |Z1|=1/sqrt((1/R)^2+(ωC)^2) Z3=1/(1/R+j3ωC) |Z3|=1/sqrt((1/R)^2+(3ωC)^2) 従って基本波と高調波の電流は |I1|=|E|/|Z1| =|E|/(1/sqrt((1/R)^2+(ωC)^2) =|E|*sqrt((1/R)^2+(ωC)^2) |I3|=|E|*h/|Z3| =|E|*h/(1/sqrt((1/R)^2+(3ωC)^2) =|E|*h*sqrt((1/R)^2+(3ωC)^2) 従って基本波と高調波の電流の最大値の比は |I3|/|I1|=|E|*h*sqrt((1/R)^2+(3ωC)^2)/|E|*sqrt((1/R)^2+(ωC)^2) =h*sqrt((1/R)^2+(3ωC)^2)/sqrt((1/R)^2+(ωC)^2) =h*sqrt(1+(3ωCR)^2)/sqrt(1+(ωCR)^2) ということになる。 |
| webadm | 投稿日時: 2009-9-6 19:57 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【41】直流分を含まない偶数波 次ぎの問題は直流分を含まない偶数波に関する興味深い問題。
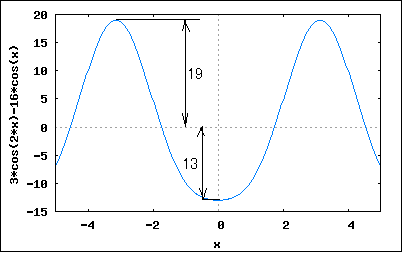 「直流分を含まない図のような波形の正弦波からのずれが主として第二高調波によるものであるとき、第二高調波と基本波の大きさの比を求めよ。」 波形を見ると偶数波であることは一目瞭然。偶数波はcos波の高調波から成る。対称波は奇数次の高調波のみから構成されるので、偶数波はかならず非対称波となる。 題意では第二高調波のみを含むということを暗にヒントとして与えているのである。 問題のひずみ波を基本波と第二高調波から成るとすると e=Em1*cos(ωt)+Em2*cos(2ωt) で表されることになる。 題意では正の最大値と負の最大値の絶対値がそれぞれ19と13ということになっている。 上のひずみ波の極大極小点を求めるために微分してみると e'=-ω*(Em1*sin(ωt)+2*Em2*sin(2ωt)) ということになる。極大点と極小点ではe'=0であることから Em1*sin(ωt)+2*Em2*sin(2ωt)=0 となるωtを求めて極大点と極小点について方程式を立てればよいことになる。 しかしどうすんだこれ。 偶関数のひずみ波の導関数はsin波のみからなる奇関数であることはわかる。 上の式の根には Em1*sin(ωt)=0かつ2*Em2*sin(2ωt)=0となる ωt=±nπ (n=0,∞) が含まれる。それ以外にも Em1*sin(ωt)=-2*Em2*sin(2ωt) となるtも含まれる。これは展開すると Em1*sin(ωt)=-2*Em2*(2*sin(ωt)*cos(ωt)) 従って Em1=-4*Em2*cos(ωt) ∴Em1+4*Em2*cos(ωt)=0 となるωtも極大極小値を取り得る。 すなわち cos(ωt)=-Em1/4*Em2 より ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) 最初の根を元のひずみ波の式に代入すると e=Em1*cos(±nπ)+Em2*cos(2*(±nπ)) =Em1*(-1)^n+Em2*cos(±2nπ) =Em1*(-1)^n+Em2 ということになる。この場合極大値と極小値はそれぞれ eMax=Em1+Em2 eMin=-Em1+Em2 ということになり、題意より eMax=Em1+Em2=19 eMin=-Em1+Em2=-13 と与えられているので、これをEm1とEm2に関する連立方程式として解くと (%i179) e1:Em1+Em2=19; (%o179) Em2+Em1=19 (%i185) e2:-Em1+Em2=-13; (%o185) Em2-Em1=-13 (%i186) solve([e1,e2],[Em1,Em2]); (%o186) [[Em1=16,Em2=3]] Em1=16 Em2=3 ということになる。確認のためにプロットしてみると wxplot2d([3*cos(2*x)+16*cos(x)], [x,-5,5])$ 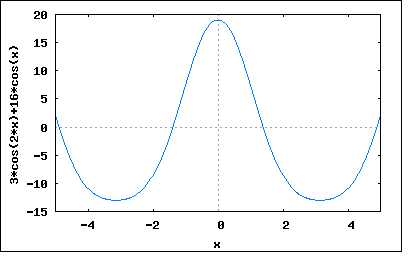 位相はずれているが確かに最大値と最小値の値はあっている。 一方もうひとつの根 ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) を代入すると e=Em1*cos(±acos(-Em1/4*Em2)±2nπ)+Em2*cos(2*(acos(-Em1/4*Em2)±2nπ)) =Em1*(-Em1/4*Em2)+Em2*cos(2*acos(-Em1/4*Em2)±2nπ) =(-Em1^2/4*Em2)+Em2*cos(2*acos(-Em1/4*Em2)) =(-Em1^2/4*Em2)+Em2*(2*cos(acos(-Em1/4*Em2))^2-1) =(-Em1^2/4*Em2)+Em2*(2*(-Em1/4*Em2)^2-1) =(-Em1^2/4*Em2)+Em1^2/8*Em2-Em2 =-Em1^2/8*Em2-Em2 ということになる。従って極大値と極小値は eMax=eMin=-Em1^2/8*Em2-Em2 どんな場合かはEm1=Em2=1と置いてプロットしてみると。 wxplot2d([cos(2*x)+cos(x)], [x,-5,5])$ 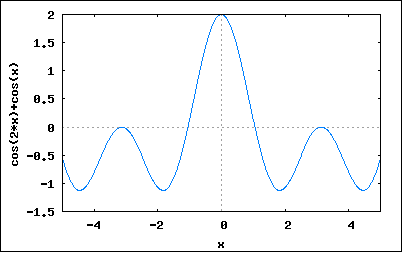 ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) =±acos(-1/4)±2nπ ωt=±1.8±2nπ のところに同じ大きさの極小点が存在することが確認できる。 そこで二つの根を組み合わせについても、もうひとつ解の存在が考えられる。 すなわち最初の根の極大値 eMax=Em1+Em2 ともうひとつの根の極小値 eMin=-Em1^2/8*Em2-Em2 で題意のeMax=19, eMin=-13を満足するEm1,Em2が存在するはずである。 解いてみると (%i229) e1:Em1+Em2=19; (%o229) Em2+Em1=19 (%i230) e2:-Em1^2/(8*Em2)-Em2=-13; (%o230) -Em2-Em1^2/(8*Em2)=-13 (%i231) solve([e1,e2],[Em1,Em2]); (%o231) [[Em1=-(16*sqrt(7)-100)/9,Em2=(16*sqrt(7)+71)/9],[Em1=(16*sqrt(7)+100)/9,Em2=-(16*sqrt(7)-71)/9]] Em1=(-16√7+100)/9, Em2=(16√7+71)/9 Em1=(16√7+100)/9, Em2=(-16√7+71)/9 という2つの組の解が得られる。実際にプロットしてみると wxplot2d([((16*sqrt(7)+71)*cos(2*x))/9+((100-16*sqrt(7))*cos(x))/9], [x,-5,5])$  中間のこぶがあるがが題意の最大値と最小値の条件は満足している。 もうひとつは別の極大値極小値の根から得たものとEm1,Em2の値は異なるが波形は同じである。 wxplot2d([((-16*sqrt(7)+71)*cos(2*x))/9+((100+16*sqrt(7))*cos(x))/9], [x,-5,5])$ 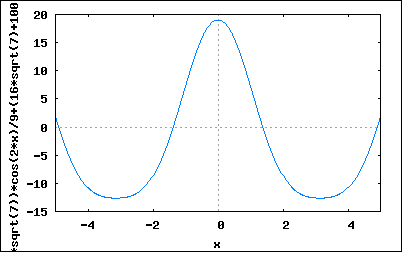 これらについて基本波と高調波の大きさの比を求めてみると最初の極大値極小値の根については Em2/Em1=3/16 =0.1875 であるのに対してもうひとつの極大値極小値の解については Em2/Em1=(-16√7+71)/(16√7+100) =0.201 Em2/Em1=(16√7+71)/(-16√7+100) =1.965 の3種類あるということになる。これが驚愕の事実である。 著者は、このもうひとつの極小極大値の根についての検討を怠って残りの2つの解の存在を見落としている。 P.S 実は組み合わせがもうひとつあって eMax=-Em1+Em2=19 eMin=-Em1^2/8*Em2-Em2=-13 これに関してEm1,Em2を解くと (%i263) e1:-Em1+Em2=19; (%o263) Em2-Em1=19 (%i264) e2:-Em1^2/(8*Em2)-Em2=-13; (%o264) -Em2-Em1^2/(8*Em2)=-13 (%i265) solve([e1,e2],[Em1,Em2]); (%o265) [[Em1=-(16*sqrt(7)+100)/9,Em2=-(16*sqrt(7)-71)/9],[Em1=(16*sqrt(7)-100)/9,Em2=(16*sqrt(7)+71)/9]] Em1=-(16√7+100)/9, Em2=-(16√7-71)/9 Em1=(16√7-100)/9, Em2=(16√7+71)/9 も解であることがわかる。確認のためにプロットしてみると。 wxplot2d([((-16*sqrt(7)-100)*cos(x))/9-((16*sqrt(7)-71)*cos(2*x))/9], [x,-5,5])$ 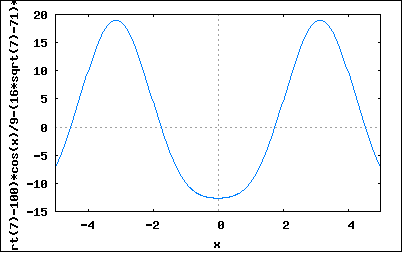 wxplot2d([((16*sqrt(7)-100)*cos(x))/9+((16*sqrt(7)+71)*cos(2*x))/9], [x,-5,5])$ 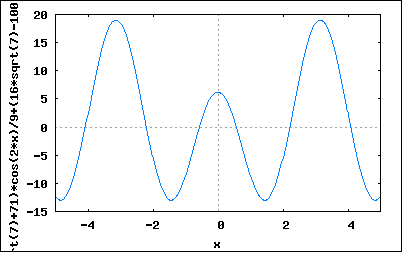 いずれも題意の最大値と最小値の条件を満足している、大発見である。 基本波と高調波の大きさの比を計算してみると Em2/Em1=(16√7-71)/(16√7+100) =-0.201 Em2/Em1=(16√7+71)/(16√7-100) =-1.965 と先の解と符号が反転しているため位相がずれて見える。 なぜ基本波と高調波の大きさが変わっただけで位相がずれて見えるのだろうか?それは読者の課題としよう(´∀` ) P.S 3 実は気になって波形を比べてみたところ、良く似ているが違っていることが発覚。 wxplot2d([3*cos(2*x)+16*cos(x),((-16*sqrt(7)+71)*cos(2*x))/9+((100+16*sqrt(7))*cos(x))/9], [x,-5,5])$ 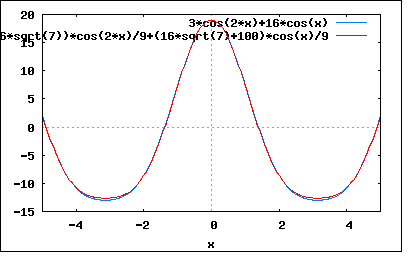 最小値が-13に若干足らない。確かにωt=πの時の値は-13にならないのである。なぜこのような解が出てきてしまったのかは謎。どこかにflawがあるのだろうか。たしかにこちらの解だと極大極小点の場所が違うので解としても怪しいのだが。しかし良く似ているのだから、少し値が違えばぴったり合う可能性もなきにしもあらず。 どうやら ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) が成り立つのは |Em1/4*Em2| ≦ 1 の場合に限定されるような気がする。最初そう思ってこの条件をつけていたが、あまりにももう一つの解が波形がぴったり似ているので条件の記述を外してしまった。 実は問題に示されているのと同じグラフを描くために e=16*cos(ωt+π)+3*cos(2ωt) =-16*cos(ωt)+3*cos(2ωt) というのを知っていたので、これも実は解である。どちらかというと問題に示されている波形はこちらなのでこっちが正解かもしれない。 この場合 Em2/Em1=-3/16 =-0.1875 ということになる。 いずれにせよスペクトルが違えば同じ波形であるはずが無いというのは確認できた。 この妙なflawの解明は読者の研究課題としよう(´∀` ) |
| webadm | 投稿日時: 2009-9-8 9:29 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【42】ひずみ波とキャパシタンス容量 次ぎの問題はひずみ波とキャパシタンス容量の関係に関するもの。以前にもそれに関する問題がありそのおさらい。
ひずみ波電圧 e=Em*(sin(ωt)+h3*sin(3ωt)) をキャパシタンスCに加えた場合の電圧実効値と電流実効値が|E|,|I|であったとするとキャパシタンスCの容量はいくらかを導けというもの。 電流の実効値は |I|=sqrt(|I1|^2+|I3|^2) |I1|=(Em/√2)*ωC |I3|=(Em*h3/√2)*3ωC 従って |I|=sqrt(((Em/√2)*ωC)^2+((Em*h3/√2)*3ωC)^2) =(Em/√2)*ωC*sqrt(1+9*h3^2) 電圧の実効値は |E|=sqrt(|E1|^2+|E3|^2) |E1|=(Em/√2) |E3|=(Em*h3/√2) 従って |E|=sqrt((Em/√2)^2+(Em*h3/√2)^2) =(Em/√2)*sqrt(1+h3^2) 電流の実効値の式よりCを導くと C=|I|/((Em/√2)*ω*sqrt(1+9*h3^2)) 電圧の実効値の式の右辺を分子に左辺を分母にそれぞれ乗じると C=(|I|/ω*|E|)*sqrt((1+h3^2)/(1+9*h3^2)) ということになる。 著者は瞬時値の式から電圧のRMS値を求めているが、電流については導出プロセスを省略していきなり実効値の式を持ち出してきている。 線形回路の重ね合わせでいけば二乗平均で実効値を求める必要もない。 |
| webadm | 投稿日時: 2009-9-8 10:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【43】半波整流波電流 次ぎの問題も少しひねった半波整流波電流に関するもの。
最大電圧Emで角周波数ωの正弦波電圧源にダイオードと電流計(可動コイル形)に抵抗が直列に接続されている場合に以下のケースそれぞれの電流計の指示を求めよというもの。 (1)ダイオードの電圧降下が0のとき (2)正方向の電流iとダイオードの電圧降下vとの関係式が次式で表されるとき v=V0+i*R0 (Vo,R0:定数) この問題のミソは、電源は正弦波だが、流れる電流は半波整流波でひずみ波である点。また電流計は可動コイル形なので指示値は平均値を意味する点。 第一の設問ではダイオードの電圧降下は無視できるので以前にあったFourier級数展開の問題のように半波整流波電流の平均値を求めればよいことになる。 第二の設問ではダイオードの電圧降下を考慮して回路に流れる半波整流波形から電流の平均値を求める必要がある。 第一のケースで流れる電流の瞬時値は i=Em*sin(ωt)/R (0≦t≦T/2) =0 (T/2≦t≦T) で表される。従って流れる電流の平均値は Iave=(1/T)∫idt (0≦t≦T) =(1/T)∫(Em*sin(ωt)/R)dt (0≦t≦T/2) =(1/T)*(Em*(1/ω-cos((ωT)/2)/ω))/R ここで ω=2π/T を代入すると Iave=(1/T)*(Em*(T/2π-cos(π)*T/2π))/R =Em/πR ということになる。 一方ダイオードの電圧降下を考慮した場合、電源電圧がV0以下の場合には電流は流れず、V0以上の場合、R0がRと直列につながった回路にV0を超えた分の電圧が加わることになる。少々やっかいである。 平均値を求めるためには黒塗りの領域の面積(積分)を求める必要がある。 ストラテジーとしては、ダイオードの順方向閾値電圧(V0)を0とした場合に回路に流れる電流の平均値を求め、それからV0を0以外とした場合に流れなくなる部分の電流の平均値を求めたものを差し引けばよいことになる。 最初にV0=0とした場合の電流は i=Em*sin(ωt)/(R0+R) (0≦t≦T/2) =0 (T/2≦t≦T) で表されその平均値は Iave0=(1/T)∫(Em*sin(ωt)/(R0+R))dt (0≦t≦T) =(1/T)∫(Em*sin(ωt)/(R0+R))dt (0≦t≦T/2) =(1/T)*(Em*(1/ω-cos((ωT)/2)/ω))/(R0+R) ここで ω=2π/T を代入すると Iave0=(1/T)*(Em*(T/2π-cos(π)*T/2π))/(R0+R) =Em/π(R0+R) ということになる。 一方V0≠0とした場合に流れなくなる電流は i=Em*sin(ωt)/(R0+R) (0≦ωt≦θ) =V0/(R0+R) (θ≦ωt≦π-θ) =Em*sin(ωt)/(R0+R) (π-θ≦ωt≦π) =0 (π≦ωt≦2π) 従ってその平均値は Iave1=(1/2π)∫(Em*sin(ωt)/(R0+R))dωt (0≦ωt≦θ) +(1/2π)∫(V0/(R0+R))dωt (θ≦ωt≦π-θ) +(1/2π)∫(Em*sin(ωt)/(R0+R))dωt (π-θ≦ωt≦π) =(1/π)*(∫(Em*sin(ωt)/(R0+R))dωt (0≦ωt≦θ) +∫(V0/(R0+R))dωt) (θ≦ωt≦π/2) =(1/π)*((Em*(1-cos(θ)))/(R0+R)+((π/2-θ)*V0)/(R0+R)) ここでθに関して以下の関係が成り立つ Em*sin(θ)=V0 従って sin(θ)=V0/Em ∴θ=asin(V0/Em) また sin(θ)^2+cos(θ)^2=1 なので (V0/Em)^2+cos(θ)^2=1 ∴cos(θ)^2=1-(V0/Em)^2 従って cos(θ)=sqrt(1-(V0/Em)^2) ということになる。 これらをそれぞれ代入すると Iave1=(1/π)*((Em*(1-sqrt(1-(V0/Em)^2)))/(R0+R)+((π/2-asin(V0/Em)*V0)/(R0+R)) =(1/π(R0+R))*((Em-sqrt(Em^2-V0^2))+(π/2-asin(V0/Em))*V0) ということになる。これをV0=0とした平均値から差し引くと Iave=Iave0-Iave1 =Em/π(R0+R)-(1/π(R0+R))*((Em-sqrt(Em^2-V0^2))+(π/2-asin(V0/Em))*V0) =(1/π(R0+R))*(sqrt(Em^2-V0^2)-(π/2-asin(V0/Em))*V0) ということになる。 著者の解は黒く塗りつぶした部分の積分だけを求めているが、結果は同じである。最終的な式は引き算の形をしているのでこちらの解法のほうが直感的かつ自然であるように思える。 |
| webadm | 投稿日時: 2009-9-9 10:46 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【44】フローティング充電電流 次ぎは半波整流波で蓄電池をフローティング充電する回路に流れる電流に関する問題。
蓄電池の電圧がE0=100Vで交流電源の実効値|E|=100V、ダイオードを含めた直列抵抗R=10Ωで可動コイル形電流計の指示値を求めよというもの。 これは実は前問の回路でV0をE0に、R0+RをRに、Emを√2|E|にそれぞれ置き換えたものとみなすことができる。 それによると流れる電流の平均値は Iave=(1/π*R)*(sqrt((√2|E|)^2-E0^2)-(π/2-asin(E0/(√2|E|))*V0) =(1/π*10)*(sqrt((√2*100)^2-100^2)-(π/2-asin(100/(√2*100)))*100) =(1/π*10)*(100-(π/2-π/4)*100) =(10*(1-π/4)/π) =0.683 [A] ということになる。 |
| webadm | 投稿日時: 2009-9-9 11:50 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【45】ひずみ波とLC並列回路 次ぎの問題はひずみ波をLC並列回路に加えた場合のひねった問題。
以下のひずみ波電圧をキャパシタンスCとインダクタンスLを並列に接続した回路に加えCを変化させたところ、電流計Aの最小値がC=0のときの値の1/2になった。第三高調波の基本波に対する割合hはいくらか求めよというもの。 e=√2|E|*(sin(ωt)+h*sin(3ωt)) LC回路に流れる電流の実効値は基本波と高調波のそれぞれの電流の実効値から |I|=sqrt(||I1|^2+|I3|^2) |I1|=|E|/|Z1| =|E|/(1/(ωC-1/ωL)) =|E|*(ωC-1/ωL) |I3|=|E|*h/|Z3| =|E|*h/(1/(3ωC-1/3ωL)) =|E|*h*(3ωC-1/3ωL) |I|=sqrt((|E|*(ωC-1/ωL))^2+(|E|*h*(3ωC-1/3ωL))^2) =|E|*sqrt((ωC-1/ωL)^2+h^2*(3ωC-1/3ωL)^2) =|E|*sqrt(9*(ω^2*C*L-1)^2+h^2*(9*ω^2*C*L-1)^2)/3ωL ということになる。 ここで見かけ上のインピーダンスを|Z|とすると |Z|=|E|/|I|=3ωL/sqrt(9*(ω^2*C*L-1)^2+h^2*(9*ω^2*C*L-1)^2) ということになる。この式の分母をCに関して微分して導関数を求めると d(9*(ω^2*C*L-1)^2+h^2*(9*ω^2*C*L-1)^2)/dC =18*ω^2*L(ω^2*C*L-1)+18*h^2*ω^2*L*(9*ω^2*C*L-1) =18*ω^4*C*L^2-18*ω^2*L+18*9*h^2*ω^4*C*L^2-18*h^2*ω^2*L =18*ω^2*L*(ω^2*C*L-1+9*h^2*ω^2*C*L-h^2) =18*ω^2*L*(ω^2*C*L*(1+9*h^2)-1-h^2) 従って|Z|が極大極小となるのは ω^2*C*L*(1+9*h^2)-1-h^2=0 を満たすCの値をとる場合であるので、これをCに関して解くと C=(1+h^2)/(ω^2*L*(1+9*h^2)) ということになる。 一方題意ではCを変化させて電流を最小値(見かけ上のインピーダンスを最大値)にした場合にC=0の時の電流の半分になったとある。 言い換えればC=0の時とCを変化させて電流を最小限にした場合の見かけ上のインピーダンスの比が1:2になるということである。 C=0の時の見かけ上のインピーダンスは |Z0|=3ωL/sqrt(9*(0-1)^2+h^2*(0-1)^2) =3ωL/sqrt(9+h^2) 電流が最大値を取るときの見かけ上のインピーダンスは |Zmax|=3ωL/sqrt(9*(ω^2*L*(1+h^2)/(ω^2*L*(1+9*h^2))-1)^2+h^2*(9*ω^2*L*(1+h^2)/(ω^2*L*(1+9*h^2))-1)^2) =3ωL/sqrt(9*((1+h^2)/(1+9*h^2)-1)^2+h^2*(9*(1+h^2)/(1+9*h^2)-1)^2) =3ωL*(1+9*h^2)/sqrt(9*(1+h^2-(1+9*h^2))^2+h^2*(9+9*h^2-(1+9*h^2))^2) =3ωL*(1+9*h^2)/sqrt(9*(-8*h^2)^2+h^2*(8)^2) =3ωL*(1+9*h^2)/8*h*sqrt(9*h^2+1) =3ωL*sqrt(1+9*h^2)/8*h ということになる。 ここでC=0の時と電流が最小の時の見かけ上のインピーダンスの比から 2*|Z0|=|Zmax| =2*3ωL/sqrt(9+h^2)=3ωL*sqrt(1+9*h^2)/8*h なる関係が成り立つことになる。これを整理すると 2/sqrt(9+h^2)=sqrt(1+9*h^2)/8*h これをhについて解くと (%i16) factor(2/sqrt(h^2+9)=sqrt(9*h^2+1)/(8*h)); (%o16) 2/sqrt(h^2+9)=sqrt(9*h^2+1)/(8*h) (%i17) %^2; (%o17) 4/(h^2+9)=(9*h^2+1)/(64*h^2) (%i18) solve([%],[h]); (%o18) [h=-sqrt(8*sqrt(13)+29)/sqrt(3),h=sqrt(8*sqrt(13)+29)/sqrt(3),h=-sqrt(29-8*sqrt(13))/sqrt(3),h=sqrt(29-8*sqrt(13))/sqrt(3)] (%i19) float(%), numer; (%o19) [h=-4.391067076224637,h=4.391067076224637,h=-0.22773507729237,h= 0.22773507729237] h=±4.391 h=±0.2277 ということになる。 hの値は正でも負でも成り立つ。また電流の実効値の式ではh^2の項しか無いので実際にはスペクトル(絶対値)が同じであれば題意の条件を満たす。正と負の違いはひずみ波の位相の違いにすぎない。 著者の解法と違う方法を試みようとしたのだが、どうしても電流が最小値になるCの条件を求めないと解けないのでそこは同じことになる。しゃくなので見かけ上のインピーダンスが2倍になるという関係からhを解いてみた。 |
| webadm | 投稿日時: 2009-9-10 7:55 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【46】RLC直列回路とひずみ波電流 次ぎの問題は以前にも出てきたような与えられたひずみ波電流が流れるために必要なひずみ波電圧を求めるもの。
以下のひずみ波電流がRLC直列回路に流すための端子電圧を求めよというもの。 i=ΣIn*sin(nωt+θn) (i=1,n) このひずみ波電流の基本波と高調波をそれぞれ等価定電流源に置き換えると、題意の端子電圧はRLC直列回路の電圧降下の瞬時値そのものである。 これも以前にあった類似の問題と同様に線形回路の重ね合わせによって求めることができる。 基本波、高調波それぞれの定電流電源に関するRLC直列回路の電圧降下の瞬時値は e1=i1*Z1 =I1*exp(j(ωt+θ1))*Z1 =I1*exp(j(ωt+θ1))*(R+j(ωL-1/ωC)) =I1*exp(j(ωt+θ1))*exp(j*atan((ωL-1/ωC)/R))*sqrt(R^2+(ωL-1/ωC)^2) ここで |Z1|=sqrt(R^2+(ωL-1/ωC)^2) φ1=atan((ωL-1/ωC)/R)) とおくと e1=I1*|Z1|*exp(j(ωt+θ1+φ1)) 従って虚数部から e1=I1*|Z1|*sin(ωt+θ1+φ1) 同様に高調波についても en=In*|Zn|*sin(nωt+θn+φn) |Zn|=sqrt(R^2+(nωL-1/nωC)^2) φn=atan((nωL-1/nωC)/R) 従って e=ΣIn*|Zn|*sin(nωt+θn+φn) ということになる。 著者の問題文の電流の式には誤植があり、Inの項が抜けている。 |
| webadm | 投稿日時: 2009-9-10 8:55 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【47】RLC混成回路のひずみ波電流 次ぎの問題はRLC混成回路に以下の様なひずみ波電圧が加えられた場合にRに流れる電流を求めよというもの。
e=E*(1+h*sin(ωt)) 一瞬全体を流れる電流を求めるかと思ってやってみたら著者の答えと合わないので問題をよく見ると、全体ではなくRに流れる一部の電流だけだった...orz とんだひっかけ問題である。 Rに流れる電流は交流分だけなので、交流電源に関してのみ計算すればよいことになる。 全体を流れる交流電流を求めると I0=E*h*sin(ωt)/Z Z=jωL0+1/(1/RL+1/(R+j(ωL-1/ωC))) ここで題意よりLC直列回路は共振しているので ωL-1/ωC=0 と置いて Z=jωL0+1/(1/RL+1/R) =jωL0+RL*R/(RL+R) 従って I0=E*h*sin(ωt)/(jωL0+RL*R/(RL+R)) Rを流れる交流電流に関して以下の回路方程式が成り立つ(分流則) I*R=(I0-I)*RL 従って I=I0*RL/(R+RL) これに先のI0を代入すると I=(E*h*sin(ωt)/(jωL0+RL*R/(RL+R)))*RL/(R+RL) =E*h*sin(ωt)*RL/(jωL0*(R+RL)+RL*R) 従ってその実効値は |I|=(E*h/√2)*RL/sqrt((ωL0*(R+RL))^2+(RL*R)^2) ここで題意よりh=0.2を代入すると |I|=(0.2*E/√2)*RL/sqrt((ωL0*(R+RL))^2+(RL*R)^2) ということになる。 ついつい並列回路のことを忘れて、L0,R,C,Lの経路だけで計算できてしまいそうに思えてしまうが、キルヒホッフの法則を忘れなければ問題ない。 |
| webadm | 投稿日時: 2009-9-11 9:35 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【48】相互誘導回路のひずみ波電流 次ぎも惑わせ問題。ずっと前に学んだ相互誘導回路が含まれていて直流電源と交流電源が混在している。
電流計A1,A2に流れる電流の実効値を求めよというもの。 A1には直流電流と交流電流が重なったひずみ波電流が流れる。A2はCで直流がブロックされているので交流電流のみが流れる。 また題意では誘導係数|M|=LでMが正と負のどちらもありえるとしている。 これも線形回路の重ね合わせを用いる。 最初に交流電源による各電流計に流れる電流の実効値を求め、次ぎにA1のみに流れる直流電流の実効値を求めてひずみ波電流の実効値を求めることにする。 交流電流は相互誘導回路のMの極性によって2通りの電流実効値を取り得ることになる。相互誘導回路を等価回路に置き換えると まず全体を流れる交流電流は |I2|=|E|/|Z| ここで Z=1/jωC+jωM+1/(1/(jω(L-M)+R)+1/(jω(L-M)+R)) =j(ωM-1/ωC)+(jω(L-M)+R)/2 =R/2+j(ω(M+(L-M)/2)-1/ωC) =R/2+j(ω(L+M)/2-1/ωC) |Z|=sqrt((R/2)^2+(ω(L+M)/2-1/ωC)^2) 従って |I2|=|E|/sqrt((R/2)^2+(ω(L+M)/2-1/ωC)^2) ということになる。 ここでM=Lの場合 |I2p|=|E|/sqrt((R/2)^2+(ωL-1/ωC)^2) M=-Lの場合 |I2m|=|E|/sqrt((R/2)^2+(1/ωC)^2) ということになる。これがA2に流れる電流の実効値ということになる。 一方A2に流れる交流電流はまったく同じ並列回路によって2分される。 A1を流れる直流電流は二つの直流電源と2つのRが環状に接続された回路を流れるのみなので I1=(E0+E0)/2*R =E0/R 従ってA1を流れるひずみ波電流の実効値は |I1p|=sqrt(|I1|^2+(|I2p|/2)^2) =sqrt((E0/R)^2+(|E|/2*sqrt((R/2)^2+(ωL-1/ωC)^2))^2) =sqrt((E0/R)^2+|E|^2/4*((R/2)^2+(ωL-1/ωC)^2)) =sqrt((E0/R)^2+|E|^2/(R^2+4*(ωL-1/ωC)^2)) |I1p|=sqrt(|I1|^2+(|I2m|/2)^2) =sqrt((E0/R)^2+(|E|/2*sqrt((R/2)^2+(1/ωC)^2))^2) =sqrt((E0/R)^2+|E|^2/4*((R/2)^2+(1/ωC)^2)) =sqrt((E0/R)^2+|E|^2/(R^2+4/(ωC)^2)) ということになる。 |
| webadm | 投稿日時: 2009-9-12 14:33 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【49】三相ひずみ波 これ以降いくつか三相ひずみ波の問題が続く。最初の問題は三相ひずみ波交流電源に負荷が接続された回路で二つ相の線電流と相間電圧がひずみ波として与えられていて、残りの相の線電流と相間電圧それに平均電力とそのスペクトルを求めよというもの。
v1=120*sin(ωt)+50*cos(3ωt) v2=80*sin(ωt+30°)+20*sin(3ωt) i1=15*sin(ωt-30°) i2=3*sin(3ωt-45°) こうした回路は三端子網もしくは三端子回路とよばれ、後に学ぶ二端子対で共通帰線があるものと同じである。本来は順序として回路網理論を学んだ後に二端子回路、二端子対回路をまなび最後にひずみ波ということになるのだが、先にひずみ波を学んでしまっているので注意が必要である。 端子間電圧の極性の取り方に注意すると、中間線のない三相交流回路のときのように以下の電圧則と電流則がなりたつ。 v1+v2+v3=0 i1+i2+i3=0 従ってv3,i3は v3=-(v1+v2) =-(120*sin(ωt)+50*cos(3ωt)+80*sin(ωt+30°)+20*sin(3ωt)) =-(120*sin(ωt)+80*(sin(ωt)*cos(30°)+cos(ωt)*sin(30°))+50*cos(3ωt)+20*sin(3ωt)) =-((120+80*cos(30°))*sin(ωt)+80*sin(30°)*cos(ωt)+50*cos(3ωt)+20*sin(3ωt)) 三角関数の合成定理より v3=-(sqrt((120+80*cos(30°)^2+(80*sin(30°))^2)*sin(ωt+atan((80*sin(30°)/(120+80*cos(30°))))+sqrt(20^2+50^2)*sin(3ωt+atan(50/20))) =-(sqrt((120+40*√3)^2+40^2)*sin(ωt+atan(1/(√3+3)))+sqrt(20^2+50^2)*sin(3ωt+atan(5/2)) =-(40*sqrt(6√3+13)*sin(ωt+atan(1/(√3+3)))+10√29*sin(3ωt+atan(5/2)) ということになる。 著者の解のv3の式には誤記があり符号が全体にかかるように括弧があってしかるべきが抜けていたり、高調波の振幅が10√29ではなく10√25と誤っている。 同様に電流も i3=-(i1+i2) =-(15*sin(ωt-30°)+3*sin(3ωt-45°)) ということになる。 一方平均電力は三相交流回路の電力は一相を基準とした他の二相の線との電力の和として求めることができるので、 Pa=(1/T)∫pdt =(1/T)∫(v2*i2-v3*i1)dt =(1/T)∫v2*i2dt-(1/T)∫v3*i1dt =(1/T)*(∫(80*sin(ωt+30°)+20*sin(3ωt))*3*sin(3ωt-45°)dt-∫(-(40*sqrt(6√3+13)*sin(ωt+atan(1/(√3+3)))+10√29*sin(3ωt+atan(5/2)))*15*sin(ωt-30°)dt) =(1/T)(∫20*sin(3ωt)*3*sin(3ωt-45°)dt+∫40*sqrt(6√3+13)*sin(ωt+atan(1/(√3+3)))*15*sin(ωt-30°)dt) =(1/T)(∫60*sin(3ωt)*(sin(3ωt)*cos(45°)-cos(3ωt)*sin(45°))dt+∫(600*sqrt(6√3+13)*(sin(ωt)*cos(atan(1/(√3+3)))+cos(ωt)*sin(atan(1/(√3+3))))*(sin(ωt)*cos(30°)-cos(ωt)*sin(30°))dt) =15√2+450√3+300 =15*(30√3+√2+20) =1100 [W] ということになる。 電力スペクトルは基本波が450√3+300で第三高調波が15√2ということになる 著者はひずみ波電力を基本波、高調波それぞれの電流と電圧の実効値と力率の積の和で表されることを利用して求めている。 |
| « 1 2 3 4 (5) 6 7 8 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

