| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-22 23:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【60】Fourier変換の推移定理
|
| webadm | 投稿日時: 2009-9-22 23:07 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【61】Fourier変換の微分と積分
|
| webadm | 投稿日時: 2009-9-22 23:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【62】Fourier変換の畳み込み積分
|
| webadm | 投稿日時: 2009-9-22 23:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【63】Fourier級数の振幅及び位相スペクトル 次ぎの問題は理論の時には出てこなかった振幅と位相スペクトルに関するもの。
命題として 実時間関数y(t)のスペクトルをF(ω)とした場合、その実数部と虚数部がωに関してそれぞれ偶関数と奇関数になることを示せ。 またF(ω)を指数表示すると F(ω)=|F(ω)|*exp(jθ(ω)) と書け、|F(ω)|を振幅スペクトル、θ(ω)を位相スペクトルと言うが前者がωに関して偶関数、後者が奇関数であることを示せ。 というもの。 一件難しそうだが、基本となるFourier変換対の式は既に学んでいるし、偶関数と奇関数の定義も知っているのでやれば出来そうである。 関数y(t)のFourier変換は F(ω)=∫y(t)*exp(-jωt)dt であるのでオイラーの公式 exp(jωt)=cos(ωt)+j*sin(ωt) より F(ω)=∫y(t)*(cos(-ωt)+j*sin(-ωt))dt =∫y(t)*cos(ωt)dt-j*∫y(t)*sin(ωt)dt ということになり、実数部と虚数部はそれぞれ Re(F(ω))=∫y(t)*cos(ωt)dt Img(F(ω))=-∫y(t)*sin(ωt)dt ということになる。 ここで偶関数の条件は F(ω)=F(-ω) なのでωの代わりに-ωを実数部の式に代入すると Re(F(-ω))=∫y(t)*cos(-ωt)dt =∫y(t)*cos(ωt)dt =Re(F(ω)) ということになり偶関数である。 一方虚数部は Img(F(-ω))=-∫y(t)*sin(-ωt)dt =∫y(t)*sin(ωt)dt =-Img(F(ω)) ということになり、これは奇関数の条件 F(ω)=-F(-ω) を満たすので虚数部は奇関数である。 またF(ω)の指数表示 F(ω)=|F(ω)|*exp(jθ(ω)) において|F(ω)|は |F(ω)|=|∫y(t)*exp(-jωt)dt| =|∫y(t)*(cos(ωt)-j*sin(ωt))dt| =sqrt((∫y(t)*cos(ωt)dt)^2+(∫y(t)*sin(ωt)dt)^2) ということになる。ωを-ωに変えると |F(-ω)|=sqrt((∫y(t)*cos(-ωt)dt)^2+(∫y(t)*sin(-ωt)dt)^2) =sqrt((∫y(t)*cos(ωt)dt)^2+(-∫y(t)*sin(ωt)dt)^2) =sqrt((∫y(t)*cos(ωt)dt)^2+(∫y(t)*sin(ωt)dt)^2) =|F(ω)| 従って|F(ω)|はωに関して偶関数である。 他方θ(ω)は θ(ω)=atan(Img(F(ω))/Re(F(ω))) ωを-ωに変えると θ(-ω)=atan(Img(F(-ω))/Re(F(-ω))) =atan(-Img(F(ω))/Re(F(ω))) =-atan(Img(F(ω))/Re(F(ω))) =-θ(ω) ということになり、これはωに関して奇関数であることを意味する。 |
| webadm | 投稿日時: 2009-9-28 13:49 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【64】直流、正弦波、余弦波のFourier変換 次ぎの問題は直流1、正弦波、余弦波のそれぞれのFourier変換を求めよというもの。
直流1のFourier変換は y(t)=1 のFourier変換であるので F(ω)=∫y(t)*exp(-jωt)dt =∫1*exp(-jωt)dt =∫exp(-jωt)dt =∫(cos(ωt)-j*sin(ωt))dt =∫cos(ωt)dt-j*∫sin(ωt)dt どうすんだこれ? 落ち着け落ち着くんだ。 よく眺めればω=0の時 F(0)=∫cos(0)dt-j*∫sin(0)dt =∫dt =∞ (ω=0) ということに気づくべきだった。 一方ω≠0の場合は F(ω)=∫cos(ωt)dt-j*∫sin(ωt)dt =0 (ω≠0) ということになる。 すなわちω=0の時のみ∞でそれ以外のωでは0となる。 しかしこれではFourier逆変換で矛盾をきたす。 どうすんだこれ? Riemann積分でもLebesgue積分でもたった1点で∞をとる関数の積分は0である。 そこで登場するのがDiracのデルタ関数という都合の良い超関数。 δ(t)=∞ (t=0) =0 (t≠0) ∫δ(t)dt=1 という性質をもつ超関数をデルタ関数と定義する。 すると先の直流1のFourier変換を F(ω)=2π*δ(ω) =2π (ω=0) =0 (ω≠0) とするとそのFourier逆変換は y(t)=(1/2π)∫F(ω)*exp(jωt)dω =(1/2π)∫2π*δ(ω)*exp(jωt)dω =∫δ(ω)*exp(jωt)dω =exp(0) =1 ということになり矛盾が解消する。 今度は正弦波sin(ω0t)のFourier変換は F(ω)=∫y(t)*exp(-jωt)dt =∫sin(ω0t)*exp(-jωt)dt =∫sin(ω0t)*(cos(ωt)-j*sin(ωt))dt =∫sin(ω0t)*cos(ωt)dt-j*∫sin(ω0t)*sin(ωt)dt =∫(sin(ω0+ω)/2+sin(ω0-ω)/2)dt-j*∫(cos(ω0-ω)/2-cos(ω0+ω)/2)dt =-j*∫(cos(ω0-ω)/2-cos(ω0+ω)/2)dt ここでω=ω0の場合 F(ω0)=-j*∫(cos(0)/2-cos(2ω0)/2)dt =-j*∫(1/2)dt =-j*∞ (ω=ω0) またω=-ω0の場合 F(-ω0)=-j*∫(cos(2ω0)/2-cos(0)/2)dt =-j*∫(-1/2)dt =j*∞ (ω=-ω0) 上記以外のωでは F(ω)=-j*∫(cos(ω0-ω)/2-cos(ω0+ω)/2)dt =0 (ω≠ω0, ω≠-ω0) ということになる。 同様にFourier逆変換が y(t)=(1/2π)∫F(ω)*exp(jωt)dω =sin(ω0t) とならねばならないので、デルタ関数を使用してF(ω)を以下のように定義する F(ω)=j*π*(δ(ω0+ω)-δ(ω0-ω)) =-j*∞ (ω=ω0) =j*∞ (ω=-ω0) =0 (ω≠ω0, ω≠-ω0) するとFourier逆変換は y(t)=(1/2π)∫F(ω)*exp(jωt)dω =(1/2π)∫(j*π*(δ(ω0+ω)-δ(ω0-ω))*exp(jωt)dω =(1/2)∫j*(δ(ω0+ω)-δ(ω0-ω))*exp(jωt)dω =(1/2)∫j*δ(ω0+ω)*exp(jωt)dω-(1/2)∫j*δ(ω0-ω)*exp(jωt)dω =(1/2)*j*exp(-jω0t)-(1/2)*j*exp(jω0t) =(1/2)*j*(cos(ω0t)-j*sin(ω0t))-(1/2)*j*(cos(ω0t)+j*sin(ω0t)) =sin(ω0t) となり矛盾しない。 同様に余弦波cos(ω0t)のFourier変換も F(ω)=∫y(t)*exp(-jωt)dt =∫cos(ω0t)*exp(-jωt)dt =∫cos(ω0t)*(cos(ωt)-j*sin(ωt))dt =∫(cos(ω0t)*cos(ωt)-j*cos(ω0t)*sin(ωt))dt =∫(cos((ω0-ω)t)/2+cos((ω0+ω)t)/2)dt-j*∫(sin((ω0+ω)t)/2-sin((ω0-ω)t)/2)dt 従ってω=ω0の場合 F(ω0)=∫(cos(0)/2+cos(2ω0t)/2)dt-j*∫(sin(2ω0t)/2-sin(0)/2)dt =∫(1/2)dt =∞ またω=-ω0の場合 F(-ω0)=∫(cos(2ω0t)/2+cos(0)/2)dt-j*∫(sin(0)/2-sin(2ω0t)/2)dt =∫(1/2)dt =∞ ということになる。 Fourier逆変換が y(t)=(1/2π)∫F(ω)*exp(jωt)dω =cos(ω0t) となるようにF(ω)を以下の様に定義すると F(ω)=π(δ(ω0+ω)+δ(ω0-ω)) =∞ (ω=ω0) =∞ (ω=-ω0) =0 (ω≠ω0, ω≠-ω0) Fourier逆変換は y(t)=(1/2π)∫F(ω)*exp(jωt)dω =(1/2π)∫π(δ(ω0+ω)+δ(ω0-ω))*exp(jωt)dω =(1/2)∫δ(ω0+ω)*exp(jωt)dω+(1/2)∫δ(ω0-ω)*exp(jωt)dω =(1/2)*exp(-jω0t)+(1/2)*exp(jω0t) =(1/2)*(cos(ω0t)-j*sin(ω0t))+(1/2)*(cos(ω0t)+j*sin(ω0t)) =cos(ω0t) となり矛盾しない。 著者はいきなりデルタ関数を使ってFourier変換結果を持ち込んでいるが、これは予め答えを知っていないとできない。デルタ関数という特殊な数式上だけ存在する超関数を導入するという数式トリックを使って初めて説明が付く。では誰が最初にこのトリックを思いついたのかというとどうやら量子物理学者のDiracらしい。デルタ関数に代表される超関数を数学的に体系だてたのは数学者のL. Schwartzである。デルタ関数を導出する方法がいくつかあるがそれは以降の問題として出てくる。 P.S 直流や正弦波交流をFourier変換するとどんなに入力信号が小さくてもスペクトルの大きさは無限大になってしまう。実際にスペクトルアナライザとかで測定するとそうはならない。これは二乗平均(RMS)値であるため積分が行われることによる。そうすると元の信号のレベルに応じた値が現れることになるからではないだろうか。デジタル信号処理などの離散Fourier変換では出力が複素スペクトル値となるため、場合によっては表現できる範囲を計算結果が超えてしまう可能性があると思われる。DSPなどではこうした積和演算時のオーバーフロー時には結果が最大値にロックされるような機構が備わっているので、汎用のCPUでの演算時のようにwrap aroundしてしまって小さな値になってしまうとかいうことは無いようになっている。またわざわざ演算後にオーバーフローしたかチェックして正の最大値に置き換えるという処理をしなくても良いようになっている。 |
| webadm | 投稿日時: 2009-9-30 5:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【65】方形パルスのFourier変換 次ぎの問題は以下の様な方形パルスのFourier変換を求めるもの。
T=1及び0.1usecの場合のスペクトルを示せというもの。 題意より入力波形は y(t)=A (-T<t<T) =0 (-T≧t≧T) これをFourier変換すると F(ω)=∫y(t)*exp(-jωt)dt (t=-∞,∞) =∫A*exp(-jωt)dt (t=-T,T) =A*((j*exp(-jωT))/ω-(j*exp(jωT))/ω) =A*(j*(cos(ωT)-j*sin(ωT))/ω-j*(cos(ωT)+j*sin(ωT))/ω) =2*A*sin(ωT)/ω ということになる。 T=1と0.1usecについてA=1と置いてプロットしてみると。 wxplot2d([(2*sin(x*10^-6))/x], [x,-5*10^6*%pi,5*10^6*%pi])$ 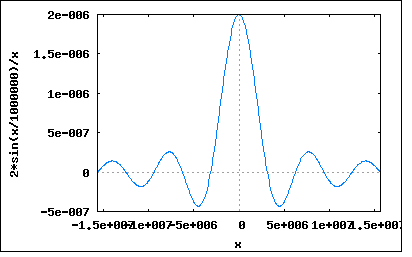 wxplot2d([(2*sin(x*10^-7))/x], [x,-5*10^7*%pi,5*10^7*%pi])$ 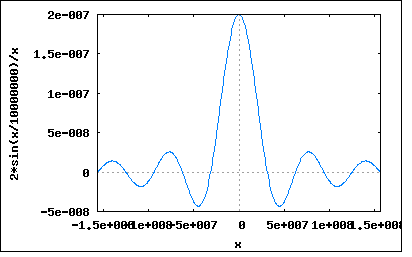 ω=0の時のピークがTの値によって変わっているのがわかる。 これは典型的なsinc関数の波形で、以下のように式を書き直すことができる F(ω)=2*A*sin(ωT)/ω =2*A*T*sin(ωt)/ωT =2*A*T*sinc(ωT) ここでsinc(0)の極限値は sinc(0)=sin(0)/0=0/0 となってしまって不確定なのだが、どうすんだこれ? これに関してはL'Hopital's rule(ロピタルの定理と呼ばれるが、実際に発見したのはその個人教師だったベルヌーイらしい)というのがあって lim f(x)/g(x) (x->0) の極限値は lim f'(x)/g'(x)=L (x->0)なる極限値が存在する場合にはそれと同じになる。 従って f(ω)=sin(ωT) g(ω)=ωT とすると f'(ω)=T*cos(ωT) g'(ω)=T となって lim f(ω)/g(ω) = lim sin(ωT)/ωT = lim f'(ω)/g'(ω) = lim T*cos(ωT)/T = lim cos(ωT)/1 (ω->0) = cos(0)/1 = 1/1 = 1 ということになる。従って lim F(ω) = 2*A*T*sinc(ωT) (ω->0) =2*A*T ということになる。このへんはほとんど解説が省略されて結果だけが示されていることが多いので難儀した。手元にある共立出版の数学公式集にはこんな極限に関する法則載っていないし。高木貞治の解析概論にも載っていない。古い解析学の本には載っていないようだ。日本では学習指導要領に含まれていないので入試問題でこのような極限値を求める際にロピタルの定理を使用して解くと逆に減点されるらしい。ロピタルの定理は教えてはいけないことになっているので、知っていることは許されないらしい。なんだそれは。 P.S 方形パルスの幅Tを∞に引き延ばすとそのFourier変換はデルタ関数に近づくのは容易にわかる。 |
| webadm | 投稿日時: 2009-9-30 9:30 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【66】単位ステップ関数のFourier変換 次ぎは以下の様な単位ステップ関数のFourier変換を求める問題。
入力関数を式で表すと y(t)=0 (t<0) =1/2 (t=0) =1 (t>0) ということになる。t=0が不連続点なのでディレクレの条件を満たすために最大値と最小値の平均値をとるものとする。 さてこれどうやってFourier変換するんだ? いろいろ調べたがいくつかやり方があるようだ。その中で一番IQが低くても理解できる方法をやってみよう。 まず第一に問題なのはy(t)がt→+∞で積分値が∞に発散してしまうのでそのままではFourier変換ができない点 そこでt→+∞で積分値が収束するように数学的なトリックを導入することにする。それはt→∞で積分値が収束するように以下の様に式を変える y(t)=exp(-at) (t>0) =0 (t<0) ただし(a>0) これをFourier変換すると F(ω)=∫y(t)*exp(-jωt)dt (t=-∞,+∞) =∫exp(-a*t)*exp(-jωt)dt (t=0,+∞) =∫exp(-(a+jω)t)dt ここでω=0においては F(0)=∫exp(-at)dt (t=0,+∞) =-exp(-∞)/a+exp(0)/a =1/a ということになる。これはa→0にするとF(0)は無限大に近づくのでデルタ関数くさい。 一方ω≠0においては F(ω)=∫exp(-(a+jω)t)dt (t=0,∞) =-exp(-∞)/(a+jω)+exp(0)/(a+jω) =1/(a+jω) これをFourier逆変換すると y(t)=(1/2π)∫F(ω)*exp(jωt)dω (ω=-∞,+∞) =(1/2π)∫(1/(a+jω))*exp(jωt)dω t=0の不連続点では y(t)=(1/2π)∫(1/(a+jω))*exp(0)dω (ω=-∞,+∞) =(1/2π)∫(1/(a+jω))dω =(1/2π)∫((a-jω)/(a^2+ω^2))dω これどうやって積分するんだ? そこでまたしても数学的なトリックを使うことに 積分範囲を(ω=-K,+K)として、それを後でK→∞として極限値を得ることにする y(t)=lim (1/2π)∫((a-jω)/(a^2+ω^2))dω (ω=-K,K) =lim (1/2π)(atan(K/a)-atan(-K/a)) (K→∞) =(1/2π)(π/2+π/2) =(1/2π)π =1/2 ということでt=0近傍の最大値と最小値の平均でディレクレの条件を満たしている。 従ってω=0の時のFourier逆変換が上記に収束するために仮に F(ω)=kπδ(ω) としてFourier逆変換を求めると y(t)=(1/2π)∫F(ω)*exp(jωt)dω =(1/2π)∫kπδ(ω)*exp(jωt)dω =(k/2)∫δ(ω)*exp(jωt)dω =(k/2)*exp(0) =k/2 ということになり、t=0の時y(0)=1/2となるためにはk=1ということになる。 従って単位ステップ関数のFourier変換は F(ω)=lim πδ(ω)+1/(a+jω) (a→0) =πδ(ω)+1/jω ということになる。 スペクトルをプロットすると 著者はこちらの解法で言うところのg(t)を(1/2)sgn(t)として、それを積分関数表記に置き換えてFourier変換を得ている。 単位ステップ関数はもともとヘビサイドが最初に用いたのでヘビサイド関数ともよばれるが、関数の定義が題意とちょっと違っていて、t=0の点が不連続のままである。 h(t)=1 (t>0) =0 (t<0) これとは別に単位ステップ関数の定義も存在する u(t)=1 (t≧0) =0 (t<0) こちらはt=0の時に1をとるというもの。このあたりの条件でFourier変換の結果が異なってくるので注意が必要だ。 これらの様々な単位ステップ関数を統一する定義としてt=0の点を任意の値に収束できるように u(t)=1 (t>0) =c (t=0) =0 (t<0) としているものもある。これらに関するFourier変換は読者の研究課題としよう。 いずれにせよFourier変換をまじめに考えると数学のトリックをいろいろ駆使しないといけない。 検索で調べるといろいろなFourier変換の表記形式によって様々なFourier変換対の形がある。それらがどういった表記形式に基づいているものか知った上で利用する必要がある。特にπが式のどこに現れるか否かに関わってくる。 P.S 最初に書いた解法にはちょっと怪しい部分があったので、まったく別の方法のものに書き換えた、これも正直マイナーなやり方のような気がするが、よく見るタイプのものと基本的に用いている手法(積分値が収束するように指数関数をかけて後で極限値をとる点)は共通である。これらのことを自分でやってみてようやくFourier変換のなんたるかが見えてきた気がする。 以前にやったFourier変換の諸性質の中で積分関数のFourier変換はこれと同じようにやればデルタ関数項が加わった変換対の式が得られるのではないだろうか。検索で調べるとそういうものがみつかるがことごとく導出方法は省略されている。 しかしまあ、デルタ関数なんて積分値が定まらないなら積分値を超法規的に定義しちゃえばいいじゃないかという発想は数学者にはできない量子物理学者ならではのもの。頭やわらかすぎ(´∀` ) |
| webadm | 投稿日時: 2009-10-1 10:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【67】余弦波バーストのFourier変換 次ぎの問題は-TからTまでの間の区間のみ余弦波がバーストする波形のFourier変換を求めよというもの。
入力波形を式で表すと y(t)=cos(ω0t) (-T≦t≦T) =0 (-T>t>T) これは以下のように書き直すことができる y(t)=f(x)g(x) f(x)=cos(ω0t) (t=-∞,∞) g(x)=1 (-T≦t≦T) =0 (-T>t>T) この場合f(x)とg(x)のそれぞれのFourier変換F(ω),G(ω)は以前の問題で既出なので、それと関数の積のFourier変換対 f(x)g(x) <=> (F*G)(ω) = (1/2π)∫F(ω')G(ω-ω')dω' によって簡単に導くことができそうである。 余弦波のFourier変換は以前の問題で F(ω)=π(δ(ω-ω0)+δ(ω+ω0)) 方形パルスのFourier変換も以前の問題で G(ω)=2*A*sin(ωT)/ω であるので、これらの合成積が求めるFourier変換ということになる。 H(ω)=∫y(t)*exp(-jωt)dt =∫f(x)g(x)*exp(-jωt)dt =(F*G)(ω) =(1/2π)∫π(δ(ω'-ω0)+δ(ω'+ω0))*(2*A*sin((ω-ω')T)/(ω-ω'))dω' =A(∫δ(ω'-ω0)*(sin((ω-ω')T)/(ω-ω'))dω'+∫δ(ω'+ω0)*(sin((ω-ω')T)/(ω-ω'))dω') =A(sin((ω-ω0)T)/(ω-ω0)+sin((ω+ω0)T)/(ω+ω0)) ということになる。 著者は合成積のFourier変換対の公式は用いず合成関数を直接Fourier変換している。 |
| webadm | 投稿日時: 2009-10-1 12:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【68】方形パルス列のFourier変換 次ぎの問題は以下の様に同一の方形パルスが2つ連続した波形のFourier変換を求めよというもの。
この波形は2つの同一で時間軸上の位置が異なる方形パルスの合成もしくは、一つの長い方形パルスの一部が3分の1の長さの方形パルス分差し引かれているものとして表すことができる。 前者だと著者と同じ解法なので、後者で解いてみよう。 波形を式で表すと y(t)=f(x)-g(x) f(t)=1 (-3T≦t≦3T) =0 (-3T>t>3T) g(t)=1 (-T≦t≦T) =0 (-T>t>T) ということになる。f(t)はg(t)の3倍のパルス幅を持つ。g(x)は以前の問題で登場したのと同じもの。従ってこのFourier変換はf(t)とg(t)のFourier変換F(ω),G(ω)の線形合成として導くことができる。 g(t)のFourier変換は以前の問題の解より G(ω)=2*A*sin(ωT)/ω f(t)のFourier変換はg(t)の時間軸を3倍引き延ばしたのと同じなので時間軸を延長した波形のFourier変換対の公式により f(t)=g(t/3) F(ω)=3*G(3*ω) =3*(2*A*sin(3ωT)/3ω) =2*A*sin(3ωT)/ω 従って求めるFourier変換は F(ω)-G(ω) =2*A*sin(3ωT)/ω-2*A*sin(ωT)/ω =(2A/ω)(sin(3ωT)-sin(ωT)) =(2A/ω)*2*cos((3ωT+ωT)/2)*sin((3ωT-ωT)/2) =4A*cos(2ωT)*sin(ωT)/ω ということになる。 |
| webadm | 投稿日時: 2009-10-1 13:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【69】正負対方形波のFourier変換 次ぎの問題も方形パルス列のFourier変換を求める問題。
以下のように符号が反転した同じ大きさのパルスが連結している波形のFourier変換を求めよというもの。 これも著者の解とは別方法で解いてみよう。 信号を式で表すと y(t)=1 (-T≦t<0) =-1 (0≦t≦T) =0 (-T>t>T) この関数は可積分(∫|y(t)|<∞)なのでそのままFourier変換してもよいが、今回はこれを微分してみよう d(y(t))/dt=δ(t+T)-2*δ(t)+δ(t-T) Fourier変換の諸性質で導関数のFourier変換は元の関数のFourier変換にjωを乗じた形となることがわかっている。 従って jωF(ω)=∫(d(y(t))/dt)*exp(-jωt)dt という関係が成り立つことから元の関数のFourier変換は F(ω)=(1/jω)∫(d(y(t))/dt)*exp(-jωt)dt =(1/jω)∫(δ(t+T)-2*δ(t)+δ(t-T))*exp(-jωt)dt =(1/jω)(∫δ(t+T)*exp(-jωt)dt+∫(-2*δ(t))*exp(-jωt)dt+∫δ(t-T)*exp(-jωt)dt) =(1/jω)(exp(jωT)-2*exp(0)+exp(-jωT)) =(1/jω)(exp(jωT)-2+exp(-jωT)) =(1/jω)(2*cos(ωT)-2) =(1/jω)(2*(2*cos(ωT/2)^2-1)-2) =(1/jω)(4*cos(ωT/2)^2-4) =(4/jω)(cos(ωT/2)^2-1) =(4/jω)(-sin(ωT/2)^2) =(j4/ω)*sin(ωT/2)^2 ということになる。 T=1とおいてプロットしてみると wxplot2d([(4*sin(x/2)^2)/x], [x,-10*%pi,10*%pi])$ 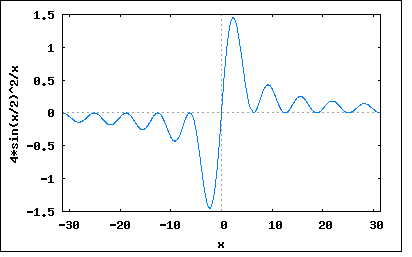 不思議な波形になる。 |
| « 1 ... 4 5 6 (7) 8 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

