| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2012-4-14 6:36 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
続々:LC直列回路 次の問題は前問と同じ回路で、初期条件が異なる。
キャパシタンスCを直流電圧Eで充電した後、インダクタンスLを通じて放電する場合、電荷および電流はどうなるか。 というもの。 初期状態でCにはC*Eなる電荷が充電されているのは明らか。スイッチを切り替えると、C側からL側へ電流が流れるにつれCに蓄えられている電荷は減少する。一方Lはそれ以前の電流0を保とうとする電圧降下が生じ、t=0でi(-0)=i(+0)=0となる。電圧の発生は電圧の印可よりも遅れるので均衡は崩れ、電流が次第に流れだし、Cの電荷が減ると同時にLの電圧降下も減じてくる。双方の電圧が0に達した時流れる電流が極大(極小)点をとり、電流は逆方向に増加していく。それを延々と繰り返すことになると予想される。 電荷量不変の理により以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 C=L=E=1としてプロットすると 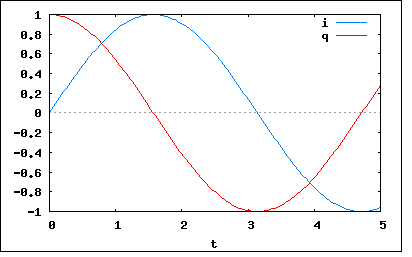 ということになる。 固有周波数は前問と同じだが、電流の振幅幅がちょっと違っている。前問ではLの二乗根に比例し、Cの二乗根に反比例したが、今度は逆である。それはエネルギーを最初に蓄えていたのがどちらかを考えれば納得がいく。 P.S 先にLに電圧が印可され、電流を0に保とうとするLの起電圧が生じるのが必ず遅れると予想した。それは正しいと思われるが、どうしてだろう。いずれ電磁気学理論で学ぶことになると思われる。 |
| webadm | 投稿日時: 2012-4-14 17:43 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
まだまだ:LC直列回路 次もLC直列回路の問題。
電源が単発パルス波形になっている点でかなり難易度が高い。 LC直列回路に継続時間T=π√LC/4、電圧Eの方形波電圧を加えた。このときの電流iを求めよ。ただし、キャパシタンスに初期電荷はなかったものとする。 パルス電源の出力電圧は0≦t≦TでE、t>Tで0となるということなので、単位ステップ関数(Heaviside関数)で以下の様に表すことができる。 従って以下の関係式が成り立つ これをHeaviside演算子で書き直すと これを演算子法で解くと ということになる。 U(t)のT時間後に現れる-U(t-T)入力に対する応答は、U(t)の応答をT時間だけシフトして極性を反転したものになる。これは信号処理などが前提としている重ね合わせの理が成り立つ線型時不変(linear Time invariant:LTI)システムで共通に成り立つ。 今まで知っているやり方を用いても同じ結果を得ることができる。それを確かめるのは読者の課題としよう( ´∀`) C=L=E=1としてプロットすると 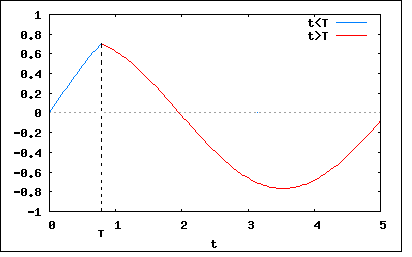 ということになる。 T時間の間にLとCに蓄えられたエネルギーがLとCの間でT>t以降交換を繰り返すことになる。 回路シミュレータでも同じ結果が得られることが確かめられる。 |
| webadm | 投稿日時: 2012-4-15 0:24 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
LC並列回路 今度はLC並列回路に関する問題。
スイッチをt=0で閉じたとき電流が振動的となるための抵抗Rの範囲およびそのときの固有周波数を求めよ。 というもの。 LC並列回路と直列に抵抗Rが接続された回路にステップ入力が加わると考えることができる。 2つの閉回路に関してキルヒホッフの電圧則により以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 新たに以下の演算子変換対を用いた 上記の解でべき根が実数である限りは振動的ではない。従って電流が振動的になるのはべき根が虚数となるケース ということになる。 ちなみにそのケースの解は ということになる。 従って固有周波数は ということになる。 R=C=L=E=1でプロットしてみると 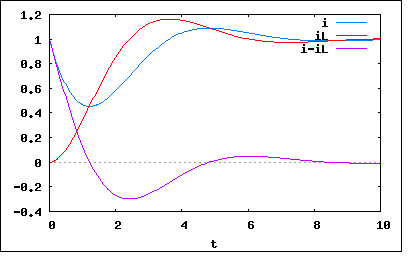 ということになる。 手元の回路シミュレータで同じ回路をシミュレートしてみると 厳密解とよく一致している。 P.S 解の検算にはMaximaを使用した。Maximaで以下の連立微分方程式を初期値問題として解くことができる。 desolve([R*diff(i(t),t,1)+(i(t)-i[L](t))/C=0,(i(t)-i[L](t))/C-L*diff(i[L](t),t,2)=0],[i(t),i[L](t)]); を実行すると Is L*(4*C*R^2-L) positive, negative, or zero? と尋ねられるので、nと答えると過減衰のケースの解が得られる。 表示された一般解の式に初期条件を代入するため subst(0, i[L](0), %); subst(E/R, i(0), %); subst(0, at('diff(i[L](t),t,1),t=0), %); expand(%); を実行すると演算子法で得たのと等価な式が得られる。 同様にpと答えて初期条件を代入すれば、振動的なケースの解が得られる 便利である。 |
| webadm | 投稿日時: 2012-4-16 3:54 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
断続部のあるLC並列回路 次の問題は断続部のあるLC並列回路
定電流源により一定電流Iが供給されていて、t=0のときi1=I,i2=0,ec=0であるとし、t=0でスイッチを閉じるとき、次の問に答えよ。(1)i1がIから0となるまでの時間Tを求めよ。(2)t=Tのときのecの値はいくらか。(3)t=0からt=Tまでの間に電源からこの回路に供給されるエネルギーを求めよ。 というもの。 定電流源というのは久々に登場。なかなかイメージがつかみきれないよね。定電圧源なら判りやすいけど。 定電流源だと一定の電流を流すためには出力電圧がいくらでも高くなるし、また低くもなるのでキルヒホッフの電圧則が電源を含んだ閉回路には使えない。 定常状態でLC直列回路に定電流が流れるというのもなかなか想像し難い。Cに電流が流れればそれに応じてCの両端の電圧が上昇する。一定の電流を流し続けるためにはLC直列回路に加える電圧を上げ続けなければならない。まさにそうした状況下でスイッチが閉じられるということになる。 スイッチが閉じる前後では鎖交磁束不変の理によりi2(-0)=i2(+0)=0であり、i1(-0)=i(-0)=Iである。しかしi2には次第に流れる電流が増す。定電流源によってi1+i2=Iであるから、i1はi2が増えた分減少していくことになる。それまではi1は一定値だったのでLの両端の電圧は0であったのが、減少に転じるとそれ以前に流れていた電流を保とうと電圧が発生する。それはCに蓄えられた電荷によって生じる電圧と逆極性となる。 予想できるのはそこまでで、それ以降はややこしくなってしまって想像の域を超えてしまう。 定常状態とするとCにどれだけの電荷が蓄えられているのか不定である。しかし問題文ではec(0)=0とあるので、実は定常状態ではCに電流が一切流れてないということが判明する。t=-0でCに蓄えられている電荷は0ということになる。 そうすると以下の様な回路として捉え直す必要がある。 すなわちt>0の定常状態ではCは短絡されていて電荷は0のまま。Lにだけ電流Iが流れている状態。t=0でスイッチが切り替わるとCとLが同時期に回路に追加される。鎖交磁束不変の理によりt=0で電流IがCに流れることになる。新たに加わったLの方はそれまでの電流0を保とうとするために逆に電流を流さないように妨げる電圧が発生する。 キルヒホッフの電流則と鎖交磁束不変の理、それに電荷量の不変の理より以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。予想外にすっきりした綺麗な式が現れた。 C=L=I=1としてプロットしてみると 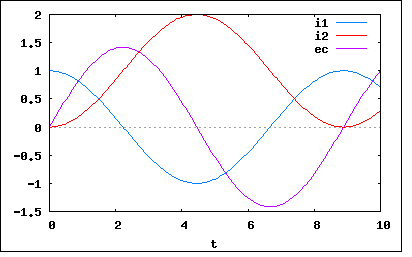 ということになる。これまた予想外なことに、i2の極大値は電源から供給される電流を超える。 さて題意(1)のi1が0となる時間Tは ということになる。 題意(2)のt=Tにおけるecの値は ということになる。 題意(3)のt=0からTの間に回路に供給されるエネルギーは、2つのLとひとつのCに供給される瞬時値電力を定積分することで ということになる。 |
| webadm | 投稿日時: 2012-4-17 9:05 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
続:断続部のあるLC並列回路 次も断続部のあるLC並列回路の問題。
図の回路は静止状態にあるものとする。いまt=0でスイッチS1を閉じ、ついでT秒後にスイッチS2を閉じるときインダクタンスLに流れる電流を求めよ。 というもの。 これも以前の問題の様に見通しを良くするために、電源とS1をステップ電圧源とし、S2を時間t<Tで0、t>Tで∞の値を取るスイッチ関数R∞(1-U(t-T))で置き換えると ということになる。 これで2つの閉回路に関してキルヒホッフの法則で立式が可能になる。 以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと ということになる。 これを演算子法で解くと ここまで来たところで、行き詰まってしまったのには訳がある。昼休みに職場の休憩所でソファーに座りながら、手にはペンとレポーお用紙を携えて毎日上の式の計算を立式からやり直した。そこでようやくわかったのだが、上の立式では解けないばかりか目的の解が得られないということだった。 どこに問題があるかは判ってしまえば当たり前である。最初の回路の電流iとiLの定義に問題があった。どちらもR∞を通るように閉回路内を流れる電流として定義している。これがまずかった。最終的に積分を計算する際にR∞→∞に移行すると0≦t≦Tの区間ではi=iL=0という解しか得られないのだ。どちらもR∞を流れるため、R∞→∞に移行するとi→0,iL→0となってしまうからだ。これは明らかに間違いである。0≦t≦Tではi=iL≠0でなければならないのだが、先の立式ではこの条件は成り立たない。 (2012/5/4) 上の見解は誤っていた。ここまでの結果でも十分R∞に関して極限操作可能であるため訂正した。 同じ結果は以下の様に定義された閉回路電流を解くことよっても得られる。 以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと ということになる。 これを演算子法で解くと これ以上の展開はmimetexで扱い切れない程長くなってしまうことが判明...orz。それだけでなくR∞(t)→∞での極限移行も困難になりそうなのでアプローチを変更(´Д`;) よく考えれば、0≦t≦TでiC=0であることは自明なので、最初に0≦t≦Tの区間とT≦tの区間とで極限移行すればよいのだった。 すなわち あとはこの積分を計算するだけということになる。計算自体は簡単だが、結果得られた式を整理するのが面倒そうだ。 (2012/5/3) 職場の昼休みに毎日この問題を最初から手計算していたのだが毎回結果が違っているように見えた。その理由が今わかった。逆行列の手計算を間違えていた...orz 逆行列を手計算で求めるには、元の行列の行列式の値を計算し、元の行列の余因子行列(Adjoint matrix)を行列式の値で割ればよいというのはもうみんな知っているよね。問題は具体的な計算方法までは数学の教科書には書いてないので自分でやってみないとわからないというのがネック。余因子行列は行列の行と列にそれぞれ直線を引いて線が引かれていないそれ以外の余った行列要素で構成される行列の行列式の値を行列要素とする行列だ(二次元行列の場合には余った行列要素は1つしかないのでそれが対応する余因子行列の行と列の要素となる。慣れればこれは暗算で出来る。問題はその前に元の行列を転置行列に変換するのだがすっかりそれを忘れていたのである。なのでMaximaで求めたのとまったく異なる結果になるのは当然。 (2012/5/4) 毎日手計算した結果、式全体が頭の中に入ってしまうとようやく見えてきた( ̄ー ̄)ニヤリ。ここまでの流れを全体的に見ると、最初の立式でも問題ないように見える。ただストレートに演算子法で解くにはi(t)の式が複雑で長くなってしまっているに過ぎない。立式を改め先にR∞の極限移行をしてしまう方法でもiL(t)の式は同じなので題意の結果を得るのが簡単になるわけではなかった。0≦t≦Tの区間ではiC=0なのでT≦tの区間について計算すれば済むが、iLに関しては0≦t≦Tの区間で0ではないのでT≦tの区間と解析接続する必要がある。これは面倒な積分式となるのは、以前に経験した通り。そこで最終的には見通しをストレートにするために、Duhamel積分の形で表して計算するというのが王道ということになる。 先のDuhamel積分を計算すると ということになる。これは非振動的なケースの場合。式が長いので途中の過程は割愛した。実際に間違いないか確かめるのは読者の課題としよう( ´∀`) 以下の条件で電流は振動的となる この場合T≦t区間の電流は ということになる。 C=R=L=T=E=1でプロットすると 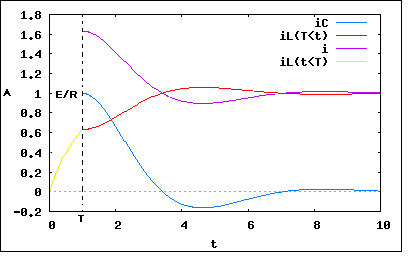 ということになる。 Tでスイッチが閉じてCに電流が流れ出しても鎖交磁束不変の理で電流iLに不連続点は生じない。Cが充電するにつれiCは減少し少しアンダーシュートしてやがて定常状態の0に近づいていく様子が見てとれる。iLは少しオーバーシュートするがやがて定常電流E/Rに近づいていく様子が見てとれる。全体を流れる電流iはt=Tで不連続点を持つ。 P.S たった3素子とスイッチング素子があるだけの回路だが解析しようとすると複雑でその挙動は即座には予想し難いものとなる。演算子法でこれも解析できたのは嬉しい。つまり19世紀のHeavisideが生きた時代でもこの種の回路は解析可能だったわけである。歴史的には一般の技術者が演算子法を回路解析に使用し始めたのは20世紀に入ってからである。日本でも戦後すぐに演算子法を使ってリレー論理回路の解析を行う試みがなされたがうまくいかなかったようだ。今日ほとんどの電気回路や電子回路、デジタル論理回路の解析はコンピューターを使って行われるのはもっともである。コンピュータが無かった時代にこの分野は数学の光が入り込めない暗黒世界であったことは容易に想像できる。それだから演算子法が厳密解を指し示す唯一の光だったわけである。 |
| webadm | 投稿日時: 2012-5-5 18:09 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
断続部のあるブリッジ回路 今度は断続部のあるブリッジ回路の問題
図のブリッジの平衡条件と検流計Gを流れる電流の波形を示せ。ただし、スイッチは毎秒n回の周期で切り替えるものとし、抵抗R3はスイッチがb側に接続されている間にキャパシタンスCの電荷が総て放電されるとみなせるぐらいに小さいものとする。また検流計の内部抵抗は無視できるものとする。 というもの。 これまでも断続部のある回路は難しかったが、これは更に難しそうである。 これも演算子法で挑戦してみよう。 これまでブリッジ回路というと上巻で直流ブリッジと交流ブリッジが登場したが、これはそのどちらでもない。 そもそも断続部が毎秒繰り返しn回スイッチングしているので平衡の概念も今まで学んできたブリッジ回路とは異なる。反応の速い検流計ならスイッチが切り替わるたびに電流が変化するので、指示値が刻々と変わることになる。 しかし題意ではそれほど応答の速い検流計を想定しているのではないようである。昔のアナログ指針のテスターを直流電圧レンジにして商用交流100Vのコンセントの電圧を測定してみれば判る通り、50か60Hzの交流には応答仕切れず指示値は0近辺で小刻みに振動する程度。針はほとんど振れないのだ。問題文では特に触れていないが、学校の実験室にあるようなアナログ式の電流計を想像すればよいのかもしれない。 そうだとすると交流と同様にその平均値が0であれば平衡とみなせると考えてよいだろう。 次に気になるのが、R3がCに充電された電荷をスイッチが離れるまでの間に放電させるのに十分小さいとはどういうことだろうか。放電の特性はCとR3の値を乗じた時定数によって定まる。時定数がより小さければより短い時間で定常状態に近づくことになる。例えばスイッチが毎秒n回切り替わるとすると、b側に接続している時間は1/n秒ということになる。もし時定数T=C*R3が1/nの更に1/5より小さければスイッチがaに切り替わるタイミングではCの電荷はほとんど0ということが期待できる。これは以前学んだ通り、時定数の5倍経過すれば定常状態に99%達するからである。 問題は検流計を流れる電流の解を解くことにある。R3に流れる電流は問われていないので、放電しきったキャパシタンスCを2/n秒毎に1/n秒間ブリッジ接続し、1/n秒後に開放するという動作を繰り返すのをどうやって式で表せばよいだろうか。 前問で断続部のある回路の演算子法での立式のやり方が少し手際良くできる道があることを発見した。時間軸上で回路が断続部によって変化する場合、その区間毎の回路構成で立式し、各区間を解析接続すればよいのである。 それでは時間軸上で回路の断続部が変化するとしてどのような順番が良いだろうか。順序は問われていないので、t=0で電荷が空のキャパシタンスCが接続された状態から初めてもよいし、開放されている状態から初めてもよいことになる。後者だと回路は完全な直流回路となり定常状態なので、やはりCが接続されたところから始めるのがよさそうである。1/n秒後にはCはブリッジから離れブリッジは不平衡状態のまま定常状態になり検流計には一定電流が1/n秒間流れ、再び放電しきったCがブリッジに接続するということを繰り返すと考えればよい。 そう考えるとこの問題はこれまでのような断続部のある回路よりは少し易しいことがわかる。キャパシタンスCがブリッジしていない状態は定常状態でGには不平衡時の定常電流が流れると考えると、キャパシタンスCを接続してから1/n秒間だけを解析すれば以降はその繰り返しということになる。 なんだ簡単じゃないか(´∀` ) t=0で電荷0のキャパシタンスCがブリッジに接続されると1/n秒後にブリッジから切り離されるまで上の回路で以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと ということになる。 これを演算子法で解くと ということになる。 一方キャパシタンスが切り離された不平衡状態で検流計に流れる定常電流は上の解でt→∞と極限移行しiC→0となる定常状態でのiGの値と同じであることから ということになる。 従ってキャパシタンスが接続されている1/n秒間は先に求めたiGの解に従って電流が流れ、キャパシタンスが切り離された1/n秒間は上のiGの電流が流れるというのを繰り返すことになる。 C=R1=R2=R4=E=1として2サイクルをプロットすると 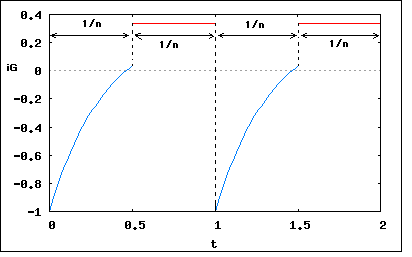 ということになる。 従って題意の平衡状態とは、電流の1サイクルの平均値が0になることであるから、キャパシタンスが接続されている1/n秒間のiGの平均値がキャパシタンスが接続されていない1/n秒間のiGの平均値を打ち消す値となる条件を見いだせばよいことになる。 キャパシタンスが接続されている区間のiGの平均値は ということになる。 一方キャパシタンスが切り離されている1/n秒間のiGの平均値は であるからして、平衡条件は ということになる。これを満足するには括弧内の式が0となる必要から ということになる。 ちなみに著者の解は最後にR2Tを左辺に移動した際に負号が付くのを忘れたのか間違った結果となっている。 |
| webadm | 投稿日時: 2012-5-5 23:12 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
RLC直列回路 これは理論の時にやった定番のRLC直列回路の問題
静止状態にあるRLC直列回路にt=0で直流電圧Eを加えた。電流および最大値を求めよ。 というもの。 RLC直列回路に電圧Eがステップ入力されたと考えることが出来る。 以下の関係が成り立つ これをHeaviside演算子で書き直すと ということになる。 これを演算子法で解くと ということになる。これは非振動的なケースで以下の条件下では振動的となる この場合解は ということになる。 問題の最大値であるが、それぞれの解の極大極小値を求めればよいことになる。 非振動的ケースで電流iが極大極小値をとる条件は ということになる。 従って極大値は上記の条件を電流の解に代入することによって ということになる。 ここで臨界減衰のケース を考えると、極大極小点は極限操作によって ということになる。一方臨界制動時の解は極限操作により ということになる。これに極大点の条件を代入すれば最大値は ということになる。 最後に振動的ケースの極大点は ということになる。n=0の時に最初の極大値に達するのでそれを解に代入すると ということになる。 それぞれのケースでの電流のカーブと、極大点について描いてみると 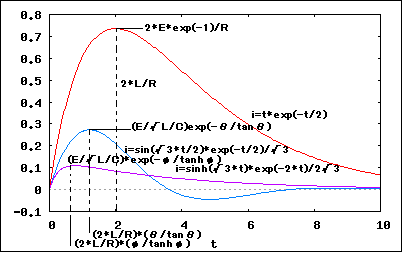 ということになる。 著者の不足制動のケースの解は電流の解の途中(最終形ではない)の誤記のある式を用いてしまっているので極大値の式が誤ったものになっている。 |
| webadm | 投稿日時: 2012-5-6 19:26 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
続:RLC直列回路 次はRLC直列回路の易しい計算問題。
RLC直列回路において、抵抗R=1[KΩ]、インダクタンスL=3[mH]なるとき、この回路が振動的であるためのキャパシタンスCの値を求めよ。 というもの。 これは前問の結果を利用すればすぐに導くことができる。 解が振動的かそうでないかは、 できまる。これをCに関する不等式に書き換えると ということになる。与えられたRとLの素子定数を代入すると ということになる。 C=0.005[uF]としてプロットするとようやく振動的なものが見えてくる 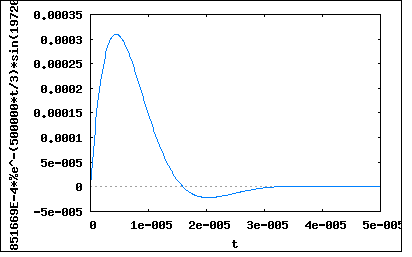 ちなみに著者の解は分母のR^2を間違えてRとして計算しているため、間違った値となっている点に注意。 |
| webadm | 投稿日時: 2012-5-6 19:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
続々:RLC直列回路 次もRLC直列回路の解析結果を知っていれば解ける簡単な計算問題。
抵抗R=6[kΩ]、インダクタンスL=90[mH]、キャパシタンスC=0.01[uF]の直列回路にt=0で直流電圧E=100[V]を加えた。流れる電流の最大値およびその時刻Tを求めよ。 というもの。 以前の問題で解析した結果を利用するには、解が過減衰か臨界減衰か振動的かを判別する必要がある。 これは前問で用いたのと同じ判別式 に値を代入してそれが正かゼロか負のいずれかを判別すればよい。 ということは臨界減衰ということになる。 その場合の極大点は以前の問題の結果より ということになる。 臨界減衰の電流の式に与えられた定数を代入して極大点付近をプロットしてみると 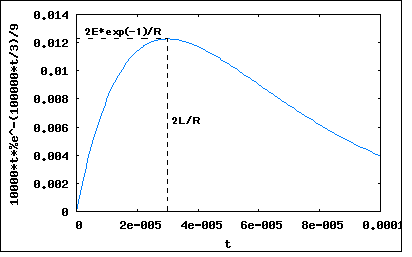 ということになり、計算値と一致していることが確認できる。 またしても著者の解はどこをどう間違えたのかTの値が倍の60usという結果になっている点に注意。 |
| webadm | 投稿日時: 2012-5-6 21:41 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
まだまた:RLC直列回路 易しい問題で少し休息したところで次ぎはまた難しそうな問題。
図の回路において、スイッチを閉じてから後、端子AB間に生じる電圧を求めよ。ただし、R=4√(L/3C)とし、スイッチを閉じる前は定常状態にあるものとする。 というもの。 回路素子数が多いので敬遠モードに入りそうだが、問題文を良く見るとスイッチがとじると右のRC直列回路はバイパスされ回路上から消失することになる。 ということはスイッチを閉じた以降は今までと同じRLC直列回路となる。 今までのRLC直列回路と異なるのは、キャパシタンスCにスイッチが閉じられる前の定常状態で初期電荷があるという点。 つまりこの問題は初期条件が異なる点を除いて今までのRLC直列回路の解析と何ら変わるものではないということがわかる。 最初に初期条件を明らかにしておく必要がある。 スイッチが閉じる前の定常状態では電流は流れておらず、2つのキャパシタンスのみにエネルギーが蓄積された状態。2つのキャパシタンスが電源電圧Eを2分圧する形で電荷を蓄えている。従ってひとつのキャパシタンスの電圧はE/2となり、蓄えられている電荷はCE/2ということになる。 スイッチが閉じるとキャパシタンスに初期電荷があるRLC直列回路に電源電圧Eがステップ入力されると考えることができる。 問題の題意から端子AB間の電圧を求めるので、予めRとCの両端の電圧に関する立式をたてるのがよさそうである。 以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 ここで端子AB間の電圧は2つの電圧の和であるので ということになる。ここでようやく題意のRの条件式を代入すると ということになる。 C=L=E=1でプロットすると 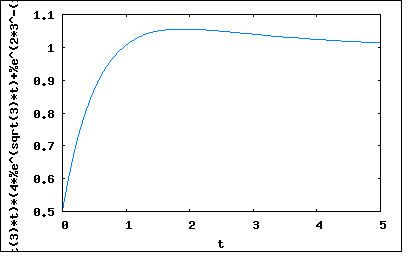 ということになる。 |
| « 1 2 3 4 (5) 6 7 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

