Gan's blog - フォーラム

(1) 2 »

投稿者	スレッド
webadm	投稿日時: 2009-10-15 7:06
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	1端子対回路下巻の第一章は一端子対回路。回路網理論の延長上にあるが、ほとんどの電気回路理論の参考書や教科書では割愛されているインピーダンス関数やBruneの定理、リアクタンス関数、逆回路、定抵抗回路などの回路網解析理論を紹介している。電気学会編の図書とかではこれらは割愛されて４端子（２端子対）回路だけで回路網理論はお終いなのが普通。ここにも著者のこだわりが感じられる。回路解析だけでなく、設計につきものの回路合成を行う場合には知っていないと損である。後に学ぶことになる過渡解析やラプラス変換で使用される複素周波数が用いられるので、複素解析に関する数学知識が前提になるのも割愛される理由かもしれない。Riemann面とか出てくるものもあるし。

webadm	投稿日時: 2009-10-15 19:22
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	複素角周波数これまで交流回路の定常状態を解析するために用いてきたインピーダンスZ(jω)式中のjωを複素角周波数 s=σ+jω で置き換えた複素関数Z(s)を新たにインピーダンス関数と呼ぶ。従って σ=0 と置くとそれは従来のインピーダンスZ(jω)の式と同じになるため、インピーダンス関数はインピーダンスをより一般化したものであると考えられる。 ωは角周波数でラジアン/秒の単位をもつ。従ってσも同様に時間当たりのなんらかの変化量を表すことになる。複素角周波数の物理的な意味は、微分方程式の一般解が Knexp(snt) で表されることを考えると良く理解できる。 sn=σn+jωn であるので、展開すると Knexp(snt)=Knexp(σn)exp(jωnt) =Knexp(σnt)(cos(ωnt)+jsin(ωnt)) ということになる。これは実数部、虚数部どちらをとっても角周波数ωnの振動とσnによる時間領域での減衰（もしくは増大）を表している。 σn=0 なら Kn(cos(ωnt)+jsin(ωnt)) となり正弦波（虚数部）、もしくは余弦波（実数部）を表し更に ωn=0 なら Kn となって直流を表すことになる。従ってσとωの値の取り方の組み合わせによって、あらゆる応答を表すことが可能になる。 σ=0 & ω=0 : 時間にかかわらず一定の直流 σ>0 & ω=0 : 時間と共に絶対値が増大する直流 σ<0 & ω=0 : 時間と共に絶対値が減少する直流 σ=0 & ω≠0 : 時間にかかわらず振幅が一定の交流 σ>0 & ω≠0 : 時間と共に振幅が増大する交流 σ<0 & ω≠0 : 時間と共に振幅が現象する交流これをグラフにプロットしてみると σ=0 & ω=0 wxplot2d([1], [x,0,100])$ σ>0 & ω=0 wxplot2d([exp(0.04x)1], [x,0,100])$ σ<0 & ω=0 wxplot2d([exp(-0.04x)1], [x,0,100])$ σ=0 & ω≠0 wxplot2d([cos(x)], [x,0,100])$ σ>0 & ω≠0 wxplot2d([exp(0.04x)cos(x)], [x,0,100])$ 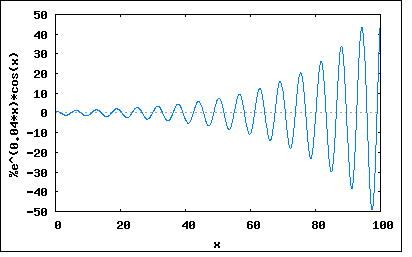σ<0 & ω≠0 wxplot2d([exp(-0.04x)cos(x)], [x,0,100])$ 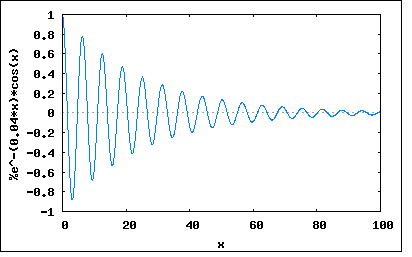σをネーパー周波数、ωをラジアン周波数と名付けたのはW. H. Huggins。 I=I0*exp(σt) の自然対数を取ると σ=(1/t)ln(I/I0) ということになりσは毎秒当たりの比率の自然対数であることからネーパー(neper)周波数と名付けられた。

webadm	投稿日時: 2009-10-15 21:47
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	インピーダンス関数既に学んだ通りインピーダンス関数は従来のインピーダンスのjωを複素角周波数で置き換えたものだが、以下のように説明することもできる。線形回路内の任意の２端子間のインピーダンスに加わる電圧V(t)と流れる電流(It)の時間領域関数を複素角周波数領域にラプラス変換したものをそれぞれV(s),I(s)とするとインピーダンス関数Z(s)は Z(s)=V(s)/I(s) =R(s)+jX(s) と表すことができる。同様にアドミッタンスについても Y(s)=I(s)/V(s) =G(s)+jB(s) と表すことができる。これとは別に以下の様に任意の有理関数が表すことができるが、それに対応する実際の回路が合成できるとは限らない。 Z(s)=(a0+a1s+...+ans^n)/(b0+b1s+...+bms^m) =f(s)/g(s) また上記の式は以下のように因数分解することができる Z(s)=H((s-s1)(s-s2)...(s-sn))/((s-sa)(s-sb)...*(s-sm)) ここでH=sn/smはスケールファクタ、ガウス大先生の代数学の基本定理によりs1,...,sn及びsa,...,smはf(s)及びg(s)の根で複素角周波数である。sがs1,...,snのいずれかの値を取るとZ(s)は０となるため零点(zero point)と呼ばれる。一方sがsa,...,smのいずれかを取る時にはZ(s)は無限大となり極(pole)と呼ばれる。重根を持つ場合には、(s-sq)^rという形になり、この場合の零点もしくは極は次数rを持つという。従って重根をもたない場合、すべての零点と極の次数は1となる。また0もしくは∞の値が零点や極である場合、上の式より (1) n > mでs=∞は次数n-mの極である (2) n < mでs=∞は次数はm-nの零点である (3) n=mでs=∞は零点や極となることはないこれらのことから零点と極が回路網解析で重要な意味を持つ。インピーダンス関数に対応する実回路が構成可能であるためには実効抵抗R(s)が常に実数でなければならないことからその有理関数であるインピーダンス関数が正実関数(positive real function)である必要があり、a,bは抵抗、インダクタンス、キャパシタンスあるいはそれらの逆数に対応することから正の実数もしくは0で、分母と分子のm,nも正の整数で\|m-n\|=0もしくは1のいずれかに制約される。これらのことはOtto Bruneによってもたらされた。 P.S 正実関数の実数部が正の実数でなければならないのは、実回路でそれに該当する実効抵抗値（インピーダンスの場合）や実効コンダクタンス（アドミッタンスの場合）が正の実数でなければならないことから自明だが、有理関数として表した場合に分子と分母の式の次数の差がたかだか０か１でなければならないというのが納得がいかない。これについては引き続き納得の行く理由を考えることにしてしばらくは鵜呑みにしよう。

webadm	投稿日時: 2009-10-16 1:11
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	正実関数(Positive Real Function) 正実関数(Positive Real Function)の定義は (1)Z(s)はsの実有理関数である (2)Re s≧0なる範囲でRe Z(s) ≧0である Z(s)が正実関数であるための必要条件は (1)Z(s)は右半平面で正則である (2)虚軸上でRe Z(s)≧0である (3)虚軸上の零点は1位で、その微係数は正である、もしくは (4)虚軸上の極は1位で、その留数は正の実数であると表される。いったいなんのことを言っているのかさっぱりわからないので、複素解析のおさらいからやる必要がありそうだ。とりあえず複素数と複素平面については知っているとして複素関数とは何かから左の複素平面(z-plane)上の複素数zを変数とするf(z)があるとき、その値もまた複素平面(w-plane)上の複素数wをとるとき、f(z)は複素関数であると定義する。なんだ当たり前じゃないか。とりあえず複素数を与えると結果も複素数になるという関数だけを考えればよいというだけである。これをインピーダンス関数を複素関数とした場合のケースに置き換えてみると sが変化するとそれに応じてインピーダンスの実数部(実効抵抗値:R）と虚数部（実効リアクタンス値:X）が決まり、Z平面上の一点に写像される。現実に構成可能な回路はR(σ,ω)は常に正の実数となるZ平面上の右半分に限定される。インピーダンス関数Z(s)が正則であるためには、以下のCauchy-Riemann方程式を満足する必要がある。といっても偏微分方程式はテキストでは書きようがないのう。こまった数式画像生成CGIを導入するしかないか。 $\frac{\partial{R}}{\partial{\sigma}}=\frac{\partial{X}}{\partial{\omega}}$ $\frac{\partial{X}}{\partial{\sigma}}=\frac{\partial{Y}}{\partial{\omega}}$ できた。しかしこれも何のことやらさっぱり。そもそも正則ってなんだ？調べてみると正則(regular)もしくは解析的(analytic)というのはCauchyの定義によると uをz=x+iyの関数とすると、zとz+δzはz平面の２つの点でuとu+δuをそれに対する関数値とする。z平面内の任意の点zに対してδu/δzがδxとδyをそれぞれ0に限りなく近づけた場合（δz=δx+iδy)に極限値を持つならば関数は正則（解析的）であるという。関数がある領域内の任意の点で正則ならばその関数はその領域内で正則であるという。ううむ、これは微分が存在するという意味なのかな。なんとなくわかるけど。それとCauchy-Riemann方程式がどういう関係があるのかというのもさっぱりわからない。ここでしばらく凍り付く(;´Д`) リーマン論文集の最初に後生がCauchy-Riemannの関係式（略してC-R関係式あるいは方程式とか偏微分方程式とかいろいろな名前で登場する）と呼ぶことになる記述が登場する学位論文がある。それによるとこうである wがzの関数であるとき $w=u(x,y)+iv(x,y)$ $z=x+iy$ とすれば無限小の差があるz平面上の２点 $z=x+iy$ $z0=x+dx+iy+idy$ とそれに対応するw平面上の２点を $w=u(x,y)+iv(x,y)$ $w0=u(x,y)+du+iv(x,y)+idv$ とするとその微分係数は $\frac{dw}{dz}=\frac{w0-w}{z0-z}$ $=\frac{du+idv}{dx+idy}$ $=\frac{(\frac{\partial{u}}{\partial{x}}dx+\frac{\partial{u}}{\partial{y}}dy+i(\frac{\partial{v}}{\partial{x}}dx+\frac{\partial{v}}{\partial{y}}dy)}{dx+idy}$ $=\frac{(\frac{\partial{u}}{\partial{x}}+i\frac{\partial{v}}{\partial{x}})dx+(\frac{\partial{v}}{\partial{y}}-i\frac{\partial{u}}{\partial{y}})idy}{dx+idy}$ ということになり、これがdx,dyの変位の仕方に関わりなく微係数が常に同一値に収束するためには分子の式で $(\frac{\partial{u}}{\partial{x}}+i\frac{\partial{v}}{\partial{x}})=(\frac{\partial{v}}{\partial{y}}-i\frac{\partial{u}}{\partial{y}})$ でなければならず、それには実数部と虚数部がそれぞれ等しくなる $\frac{\partial{u}}{\partial{x}}=\frac{\partial{v}}{\partial{y}}$ $\frac{\partial{v}}{\partial{x}}=-\frac{\partial{u}}{\partial{y}}$ が唯一wがzの（正則）関数である必要十分条件であるとしている。この前の式までの過程を理解していないと最後の式だけ示されても意味がさっぱりわからないのである。Riemannの論文ではdw/dzからいっきに飛んで核心的な部分だけを説明しているので、その導出方法は読み手に委ねられている。Riemannは天才で、度々こうした飛躍がみられ常人はそこで思考がついていけず止まってしまう傾向があり、以来飛躍的なアイデアは人前では控えめな表現に止めるようになったらしい。Riemannの論文では単にwがzの関数である必要十分条件であるとだけしか言っていないので当時まったく話題にもならなかったのだが、後生の時代になってこれが複素関数が正則である必定十分条件であることが再認識され今日に至る。調べてみると結構多くの本で最後のC-R関係式だけ示して終わっているものが多い。これだけですべて理解できたらRiemannと同じ天才に違いない。IQの低い者にとっては地道に積み重ねてやっとたどり着けるありさま。解析学の丁寧な本ではそれぞれの著者の解釈によって関係式にたどり着く過程が示されている。まあ、それを見ずしてもRiemannの論文を見ればわかるのではあるが。現在はインターネット上でドイツ語原文から書き起こしたPDFドキュメントが公開されているので一読されると良いだろう。で話はまだ終わっていない。 (3)虚軸上の零点は1位で、その微係数は正である、もしくは (4)虚軸上の極は1位で、その留数は正の実数であるこれの意味するところが何なのかさっぱりわからない。微係数はわかっているが、留数ってなんだっけ？零点と極の位数が1なのは有理関数の分子と分母の次数の差が1以内ということから明らかではあるが。学生時代に確か留数定理の講義を受けた記憶は確かにあるが、何に使うのかは知らずに複素平面になんか○だか×だかのある図以外はすっかり忘れてしまった。まず虚軸上ということは、等価抵抗は0ということになりかつs=±jωでリアクタンスからのみなる回路ということになる。 Z(jω)=jX(jω) これが0になるωが零点だが、キャパシタンスの場合ω=±∞、インダクタンスの場合ω=0が該当する。いずれにせ常にωが正に増加するとリアクタンスも正に増加するので dX/dω > 0 ということになる。従って虚軸上に零点を持つ場合、その微係数は正の値を持つと言える。一方、虚軸上で極を持つとはどういうことか？ Z(jω)=±j∞ となるωを意味し。これはキャパシタンスが直列に接続された回路でω=0の時、インダクタンスが直列に接続された回路でω=±∞の時それぞれインピーダンスが無限大をとるのに該当する。当然それらの極においてはインピーダンス関数Zの微係数は定まらないので正則ではない(irregular)。では虚軸上に極を持つ場合留数が正の実数であるとはどういう意味か？留数(Residues)の定義は手元の"A COURSE OF MODERN ANALYSIS" E.T WHITTAKER, G.N WATSON著の"6.1 Residues"で解説されている関数f(z)がz=aに次数mの極をもつ場合、以下の式で表される。 $f(z)=\frac{a_{-m}}{(z-a)^m}+\frac{a_{-m+1}}{(z-a)^{m-1}}+...+\frac{a_{-1}}{z-a}+\phi(z)$ ここで $\phi(z)$ はz=aとその近傍で正則である。係数 $\small{a_{-1}}$ が極aに関する関数f(z)の留数と呼ぶというもの。これも天下り的でなんのことやら。この分だと二三日は十分寝込みそう(;´Д`) この辺の理屈は数学の複素解析では円環状にいくつもの定理がつながっていて、ひとつの定理は別の定理を前提にしていて、ちょうど一匹の蛇が別の蛇の尻尾を噛んでいて、それを調べようとするとまた別の定理では他の定理の尻尾を噛んでいるのに気づいて、ぐるっと調べていくと最初に調べた定理の尻尾を噛んでいたのが最後に行き着いた定理だったという堂々巡りに行き着く。それでやっと全体の辻褄があっているということに気づくことになる。これは珍しく数学では多くの定理が皆どっかでつながっていて調和を成しているという点で複素解析は美しいとされているらしい。まあ数学は蟻の巣穴みたいなもので、好き勝手に掘り進んでいったら反対側からも掘り進んでいたのとはち合わせして互いがつながりあったというのはよくある話。円環状につながってしまった後で見てもどこが発端かなんかはもう誰にもわからない。これとはまったく別途に電気工学の世界では、ちょうど第二次世界大戦前に真空管が発明され、抵抗とコンデンサとコイルを組み合わせて目的の用途と特性を備えた増幅器やフィルターをどうやって設計するかという問題に数多くの先端技術者や研究者が挑んでいた。中でも信号伝送やアナログ信号処理（アナログコンピューター）の研究の最先端を行っていた米国には世界中から優秀な技術者や研究者が集まっていた。それまで伝送回路やフィルターを数式でモデル化し解析する理論はあったが、意図した特性の回路を合成する理論は無く、試行錯誤と経験が頼りだったが、この頃回路網合成理論がめざましい発展をとげた。ほとんどの基本概念は戦前に米国に招かれていたドイツ人のWilhelm Cauerによって米国人の先駆者Fosterのリアクタンス関数理論に触発されて独自に発展させたものだった、後にMITで彼の下で博士号を得た米国系ドイツ人Otto Bruneによって正実関数の必要十分条件や回路網合成理論が現在教えられている形に整理された。Cauer自身は第二次世界大戦が始まるとドイツに帰国し、その家族はベルリンを離れ疎開したものの、彼自身は助言に逆らってソ連軍によって陥落する直前のベルリンに戻り、終戦後に隣家の庭で無惨にも処刑された遺体として発見された。当時出版を予定していた本の第二巻の原稿は戦火で失われたが、遺族らがその後遺稿を整理して出版しその偉業が世に知られるに至った。こうした戦争で翻弄された偉大な研究者の生涯を知ると涙無くしては語れない。詳しいことはPrinceton大学が公開している以下の資料を参照されたい。 Life and Work of Wilhelm Cauer (1900 – 1945) 話を正実関数に戻すと先の留数の定義の式はLaurent定理のz=aの近傍に関するf(z)のLaurent級数展開 $f(z)=\sum_{n=1}^\infty \frac{a_{-n}}{(z-a)^n}+\sum_{n=0}^\infty b_{n}(z-a)^n$ $=\frac{a_-m}{(z-a)^m}+\frac{a_{-m+1}}{(z-a)^{m-1}}+...+\frac{a_{-1}}{z-a}+\sum_{n=0}^\infty b_{n}(z-a)^n$ で最後の項はz=aを含めその近傍で正則なので $\phi(z)=\sum_{n=0}^\infty b_{n}(z-a)^n$ と置き換えたものである $f(z)=\frac{a_{-m}}{(z-a)^m}+\frac{a_{-m+1}}{(z-a)^{m-1}}+...+\frac{a_{-1}}{z-a}+\phi(z)$ ということだった。ここで閉路Cとそれを含む領域D内にある孤立特異点z=a1,...,anを除いて正則な関数f(z)の積分は各孤立特異点を中心としてそれを取り囲む円をα、β、γ,...とすると $\oint_C f(z)dz=\oint_\alpha f(z)dz+\oint_\beta f(z)dz+\oint_\gamma f(z)dz+...\\=2\pi a_{-1}+2\pi b_{-1}+2\pi c_{-1}+...\\=2\pi i\sum_{i=1}^n \operatorname{Res}$ で決まるという留数定理というのがつながってくる。ここでΣResは孤立特異点に関する留数の総和である。ここで先のLaurent展開式の積分を考える。積分経路を中心点をaとしφ(z)がその内部で正則である半径ρの円とすると $\oint_a f(z)dz=\sum_{n=1}^m a_{-n}\oint_a \frac{dz}{(z-a)^n}+\oint_a \phi(z)dz$ CAUTHYの積分定理により正則な関数φ(z)の積分項は $\oint_a \phi(z)dz=0$ となる。またn=1以外では $z-a=\rho e^i\theta$ と置き換えることにより $\oint_a \frac{dz}{(z-a)^n}=\int_0^{2\pi}\frac{\rho e^{i\theta}id\theta}{\rho^n e^{ni\theta}}=\rho^{(1-n)}\int_0^{2\pi}e^{(1-n)i\theta}id\theta=\rho^{(1-n)}\left[\frac{e^{(1-n)i\theta}}{1-n}\right]_0^{2\pi}=0$ ということになる。 n=1の場合だけが $\oint_a \frac{dz}{z-a}=\int_0^{2\pi}\frac{\rho e^{i\theta}id\theta}{\rho e^{i\theta}}=\int_0^{2\pi}id\theta=2\pi i$ となるので $\oint_a f(z)dz = 2\pi i a_{-1}$ ということになり留数は $\operatorname{Res} = a_{-1}$ ということに帰着する。インピーダンス関数を部分分数に展開できれば留数が正の実数であるかどうかで正実関数（受動素子のみで合成可能）であるかどうかが判断できることになる。たとえば $Z(s)=\frac{2s+1}{s(s-3)}$ が正実関数がどうかは、展開してみればわかるので $Z(s)=\frac{k_1}{s}+\frac{k2}{s-3}$ と展開できるとするとヘビサイドの展開定理を使ってs(s-3)を両辺に乗じると $2s+1={k_1}{(s-3)}+{k_2}{s}$ s=0を代入すると k1=-1/3 s=3を代入すると k2=7/3 従ってk1<0なので極の次数は１次だが留数が正ではないものがあるためこれは正実関数ではないということになる。あと最初から極がS平面の右側にあるという点ですでに正実関数ではないのだが。正実関数は虚軸上にしか孤立特異点をもたない。こやって実際のインピーダンス関数の式を展開していくと実際の素子に対応する項(抵抗、インダクタンス、キャパシタンス）に分解されるが、それぞれの係数が正の実数であればそれぞれ受動素子の定数となるため現実の回路が合成できることを確かめることができる。これらはいくつか演習を繰り返すことによって実感がつかめることになる。 P.S 戦後になって回路網理論は大阪大学名誉教授　尾崎弘氏によって能動素子（負性抵抗素子）や理想変成器（負のインピーダンスやキャパシタンスを持つジャイレーター）、集中定数回路や分布定数回路を混在したものを扱えるように多変数複素関数に拡張されたが唯でさえ複素周波数変数を使用した回路網理論は難しいのでほとんど学校では時間を割いてまで教えられていない。手元に尾崎氏の著者「大学課程電気回路（２）第3版」がある。最新の改版で再び複素周波数変数を使用した回路網理論の章が多くの希望で復活したといういきさつが改版の前書きに書かれている。おそらく一端割愛した理由は昨今の計算機の能力の飛躍的な向上とアナログ回路素子メーカーがフィルター設計ソフトを無償提供しているため理論を知らなくても任意のフィルターが設計できてしまうという時代変化があるのではないだろうか。これは進歩なのか退化なのか。といっても本書が扱う基礎的な複素周波数変数を使った回路網理論ではあくまで受動素子（抵抗、インダクタンス、キャパシタンス）のみで構成される回路のみを扱うため、負性抵抗や負性インダクタンスやキャパシタンスを構成する能動素子は含まれず、集中定数回路に範囲が制約されるのはいたし方がない。更に拡張された回路網理論を知るにはaffine換群や複素多様体、リーマン面、多変数複素関数論とかを知っている必要があるそうだ。 P.S 留数定理に関する内容をWikipediaのものから、手元の"A COURSE OF MODERN ANALYSIS"にあるものをベースに書き換えた。Wikipediaにある内容も式の表記を除いて基本的には同書をバイブルしたものであると思われる。ヘビサイドと同時代の数学者でヘビサイドの奇妙な演算子法に興味を示し、その奥義を直接手紙で教えてもらい、後にラプラス変換と呼ばれる演算子法にとって代わって教えられるようになった複素積分の応用を研究していたケンブリッジ大学のBromwichは演算子法に関する疑問に応えてもらう代わりに留数定理をヘビサイドに教えようとしたが徒労に終わったらしい(´∀` )　Bromwichはラプラス逆変換も複素積分(Bromwich積分）で表したが、今日ですらそれを使う人なんていない。みんな演算子法と同じように部分分数に展開して変換対の表から逆変換結果を得ている。Bromwichには黒歴史があり、ヘビサイドから懇切に教えてもらった手紙は一切残されていないが、Bromwichからヘビサイドに送った手紙が残っており、ヘビサイドの返事は常に迅速かつ量的にも多かったらしいことがうかがわれるとか。当時演算子法は批判の矢面にたっていただけに、興味を示してくれる数学者には懇意にすべてを伝えようとしたのかもしれない。

webadm	投稿日時: 2009-10-22 7:47
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	リアクタンス関数戦前の1924年に米国ベル研究所の研究者Ronald Fosterの論文"A Reactance Theorem"が発表され、回路網合成の歴史が動き始めた。 Fosterは駆動点インピーダンス(driving point impedance)という言葉を用いインダクタンスとキャパシタンスのみから成り抵抗を含まない２端子回路が複素周波数変数を用いた代数式によって表され、その式を部分分数に展開すれば対応する回路が合成できることと、その必要十分条件を初めて示した。この時既にLCのみの回路に限定されるが正実関数の定義が与えられている。当時米国に居たドイツ人CauerはFosterの論文に触発され、すぐさまその拡張と一般化のアイデアを得、Fosterの仕事の続きをすることになる。Cauerは抵抗を含む２端子回路にも適用できるようにFosterのリアクタンス理論を拡張し、更にラダー接続回路の合成が可能な連分数展開も組み入れた。これは後に次ぎに学ぶことになる。最初のOtto Bruneの正実関数が出てきて歴史的に逆になってしまうが、ここでようやく最初に登場したFosterのリアクタンス理論から学ぶことにしよう。最初に１端子対回路（２端子回路）はn端子対回路の一端子対以外を除いてすべて短絡した回路と考えると一般化することができる。左のn端子対回路では以下の回路方程式が成り立つ $\begin{pmatrix}Z_{11} & Z_{12} & Z_{13} & ... & Z_{1n} \\ Z_{21} & Z_{22} & Z_{23} & ... & Z_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ Z_{n1} & Z_{n2} & Z_{n3} & ... & Z_{nn} \end{pmatrix}\begin{pmatrix}I_1 \\ I_2 \\ . \\ . \\ . \\ I_n \end{pmatrix}=\begin{pmatrix}E_1 \\ E_2 \\ . \\ . \\ . \\ E_n \end{pmatrix}$ 一方1端子対回路ではポート1以外をすべて短絡したのと等価なので端子電圧は0となり $\begin{pmatrix}Z_{11} & Z_{12} & Z_{13} & ... & Z_{1n} \\ Z_{21} & Z_{22} & Z_{23} & ... & Z_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ Z_{n1} & Z_{n2} & Z_{n3} & ... & Z_{nn} \end{pmatrix}\begin{pmatrix}I_1 \\ I_2 \\ . \\ . \\ . \\ I_n \end{pmatrix}=\begin{pmatrix}E_1 \\ 0 \\ . \\ . \\ . \\ 0 \end{pmatrix}$ ということになる。従って両辺にインピーダンスマトリックスの逆行列を乗じると $\begin{pmatrix}I_1 \\ I_2 \\ . \\ . \\ . \\ I_n \end{pmatrix}=\begin{pmatrix}Z_{11} & Z_{12} & Z_{13} & ... & Z_{1n} \\ Z_{21} & Z_{22} & Z_{23} & ... & Z_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ Z_{n1} & Z_{n2} & Z_{n3} & ... & Z_{nn} \end{pmatrix}^{-1}\begin{pmatrix}E_1 \\ 0 \\ . \\ . \\ . \\ 0 \end{pmatrix}$ $=\frac{\begin{pmatrix}\Delta_{11} & \Delta_{12} & \Delta_{13} & ... & \Delta_{1n} \\ \Delta_{21} & \Delta_{22} & \Delta_{23} & ... & \Delta_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ \Delta_{n1} & \Delta_{n2} & \Delta_{n3} & ... & \Delta_{nn} \end{pmatrix}}{\left\|\begin{matrix}Z_{1,1} & Z_{12} & Z_{13} & ... & Z_{1n} \\ Z_{21} & Z_{22} & Z_{23} & ... & Z_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ Z_{n1} & Z_{n2} & Z_{n3} & ... & Z_{nn} \end{matrix}\right\|}\begin{pmatrix}E_1 \\ 0 \\ . \\ . \\ . \\ 0 \end{pmatrix}$ $=\begin{pmatrix}\frac{Delta_{11}}{\Delta} & \frac{\Delta_{12}}{\Delta} & \frac{\Delta_{13}}{\Delta} & ... & \frac{\Delta_{1n}}{\Delta} \\ \frac{\Delta_{21}}{\Delta} & \frac{\Delta_{22}}{\Delta} & \frac{\Delta_{23}}{\Delta} & ... & \frac{\Delta_{2n}}{\Delta} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ \frac{\Delta_{n1}}{\Delta} & \frac{\Delta_{n2}}{\Delta} & \frac{\Delta_{n3}}{\Delta} & ... & \frac{\Delta_{nn}}{\Delta} \end{pmatrix}\begin{pmatrix}E_1 \\ 0 \\ . \\ . \\ . \\ 0 \end{pmatrix}$ $=\begin{pmatrix}\frac{\Delta_{11}}{\Delta}E_1 \\ \frac{\Delta_{21}}{\Delta}E_1 \\ . \\ . \\ . \\ \frac{\Delta_{n1}}{\Delta}E_1 \end{pmatrix}$ ただし $\Delta=\left\|\begin{matrix}Z_{1,1} & Z_{12} & Z_{13} & ... & Z_{1n} \\ Z_{21} & Z_{22} & Z_{23} & ... & Z_{2n} \\ . & . & . & & . \\ . & . & . & & . \\ . & . & . & & . \\ Z_{n1} & Z_{n2} & Z_{n3} & ... & Z_{nn} \end{matrix}\right\|$ I1について解くと $I_1=\frac{\Delta_{11}}{\Delta}E_1=\frac{E_1}{\frac{\Delta}{\Delta_{11}}}$ 従ってポート１の駆動点インピーダンスは $Z=\frac{E_1}{I_1}=\frac{\Delta}{\Delta_{11}}$ ということになる。インピーダンスマトリックスの任意の要素Zijが損失の無いLとCからなるとするとs=jωとすると $Z_{ij}=s L_{ij}+\frac{1}{s C_{ij}}$ $=\frac{1}{s}\left(s^2 L_{ij}+\frac{1}{C_{ij}}\right)$ $=\frac{L_{ij}}{s}\left(s^2+\frac{1}{L_{ij} C_{ij}}\right)$ ここで $\omega_{ij}=\frac{1}{\sqrt{L_{ij} C_{ij}}$ と置くと $Z_{ij}=\frac{L_{ij}}{s}\left(s^2+{\omega_{ij}}^2\right)$ 従って $\Delta=Z_{11} Z_{22} ... Z_{nn}+...$ $=\frac{L_{11}}{s}\left(s^2+{\omega_{11}}^2\right) \frac{L_{22}}{s}\left(s^2+{\omega_{22}}^2\right) ... \frac{L_{nn}}{s}\left(s^2+{\omega_{nn}}^2\right)+...$ $=\frac{a_n}{s^n}\left(s^{2n}+a_{n-1}s^{2(n-1)}+...+a_{1}s^2+a_0\right)$ ここで $\Delta=0$ を満たすn個の根をそれぞれ ${\omega_1}^2,{\omega_3}^2,...,{\omega_{2n-1}}^2$ とすると $\Delta=\frac{b_n}{s^n}\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)$ 同様に $\Delta_{11}=Z_{22} Z_{33} ... Z_{nn}+...$ $=\frac{L_{22}}{s}\left(s^2+{\omega_{22}}^2\right) \frac{L_{33}}{s}\left(s^2+{\omega_{33}}^2\right) ... \frac{L_{nn}}{s}\left(s^2+{\omega_{nn}}^2\right)+...$ $=\frac{b_m}{s^{n-1}}\left(s^{2(n-1)}+b_{m-1}s^{2(n-2)}+...+b_{1}s^2+b_0\right)$ $=\frac{b_m}{s^{n-1}}\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)$ 従って駆動点インピーダンスZ(s)は $Z(s)=\frac{\frac{a_n}{s^n}\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{\frac{b_m}{s^{n-1}}\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ $=H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ 従って分子が偶関数で分母が奇関数の有理関数となる。分子と分母の式を多項式に展開すると分子の式の次数は2nで分母の次数は一つ少ない2n-1となる。 $s=j\omega$ とすると、 $s=\pm{j\omega_1},\pm{j\omega_3},...,\pm{j\omega_{2n-1}}$ は駆動点インピーダンスが0となる零点である。また $s=0,\pm{j\omega_2}, \pm{j\omega_4},...,\pm{j\omega_{2n-2}}$ は駆動点インピーダンスが∞となる極である。ただし $\omega_1=0$ であるケースでは、 $\left(s^2+{\omega_1}^2\right)=s^2$ となり、最後の式の分母のsと相殺されて分子が奇関数で分母が偶関数となり $Z(s)=s H \frac{\left(s^2+{\omega_{3}}^2\right)\left(s^2+{\omega_{5}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ こんどはω=0が極ではなく零点となる。この場合でも分子と分母を展開して多項式にすると分子の次数は2n-1で分母の次数は2n-2である。依然として分母の次数が分子より1少ない。また同じ値を零点と極で持つ場合には、分子と分母で相殺されてそれは零点でも極でも無くなる。ところで $s=\pm{j\infty}$ の場合には、駆動点インピーダンスはどうなるのだろうか？いろいろ調べると全部でパターンが４つあるらしいが、２つほど納得がいかん(;´Д`) どうやら先に導いた２つの駆動点インピーダンスの式においてω=∞に零点もしくは極を持つケースをそれぞれ考えると４種類に分かれることがようやく見えてきた。その前に零点と極の位置関係や大小関係や零点の近傍で微係数が正であるかどうかが気になる。このあたりがFoster Reactance Theoremで最も重要な部分であるが、ほとんどの書では結論だけが示されていて導出過程についてはほとんど触れられていないか天下りな説明になっている。当時のFosterの論文はBell研のジャーナルに掲載されていたので一般には公開されていない（戦前限られた研究機関や大学にしか配布されていなかった）し、あったとしてもベル研が無くなった今では廃棄処分されてもう手に入らないだろう。こうなったらFosterの偉業を追体験するしかあるまい。先に駆動点インピーダンスの式を見る限り、零点と極の出現順序は式上は任意であるように見える。しかし本当にそうだろうか？前出の駆動点インピーダンスの式はLとCのみからなるリアクタンス関数であるが、リアクタンス関数は奇関数であることを確かめてみよう。奇関数の定義から Z(-s)=-Z(s) が成り立つ必要がある。リアクタンス関数の式にsの代わりに-sを代入すると $\begin{array}{rcl}Z(-s) &=& -H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& -Z(s)\end{array}$ $\begin{array}{rcl}Z(-s) &=& -s H \frac{\left(s^2+{\omega_{3}}^2\right)\left(s^2+{\omega_{5}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& -Z(s)\end{array}$ ということになり奇関数であることが証明された。次ぎなる問題は零点と極の数について。リアクタンス関数が正実関数であるためには、分子と分母の多項式の次数の差がたかだか１でなければならないことは既に学んだ通り。そのことから、リアクタンス関数の式で分子の項（零点に対応）と分母の項（極に対応）の数は同数でなければならないことになる。従ってリアクタンス関数の零点と極の数はω=0を除いては同数でなければならないことになる。またω=0を除いて零点及び極は互いに共役な複素数で虚軸上にのみ対で現れることになるのも明らか。すると零点と極は虚軸上にどのような順番で現れるのかというのが疑問として残る。ある本では天下り的に、別の本ではいくつかの回路例で定性的に零点と極が交互に現れるとしているが一般的になぜそういえるのか？それにはまず先のリアクタンス関数の式でs=jωとしてみる必要がある ω=0に極をもつケースは $Z(j\omega)=-j H \frac{\left({\omega_{1}}^2-\omega^2\right)\left({\omega_{3}}^2-\omega^2\right)...\left({\omega_{2n-1}}^2-\omega^2\right)}{\omega \left({\omega_{2}}^2-\omega^2\right)\left({\omega_{4}}^2-\omega^2\right)...\left({\omega_{2n-2}}^2-\omega^2\right)}$ 一方ω=0に零点を持つケースは $Z(j\omega)=j\omega H \frac{\left({\omega_{3}}^2-\omega^2\right)\left({\omega_{5}}^2-\omega^2\right)...\left({\omega_{2n-1}}^2-\omega^2\right)}{\left({\omega_{2}}^2-\omega^2\right)\left({\omega_{4}}^2-\omega^2\right)...\left({\omega_{2n-2}}^2-\omega^2\right)}$ ということになる。ここでもし $\omega_1>\omega_2$ だとすると、最初の式ではωが0でZ=-j∞の極を持ち、ωが増加するにつれ分子と分母は共に減少するが分母の方が分子よりも先に0になるためZははじめ増加するものの途中で再び減少し最初の極で-j∞になってしまうことになる。これは明らかに極以外では微係数が正でなければならない正実関数に反する。別の言い方をすれば留数が負の値をもつものがあるという意味で正実関数ではなく、受動素子LとCだけでは回路を構成することができないということになる。例えば $Z(j\omega)=-j\frac{\left(2-\omega^2\right)\left(3-\omega^2\right)}{\omega \left(1-\omega^2\right)}$ というようなリアクタンス関数を考えてみると、これをω=0とω=1の間でプロットしてみると wxplot2d([-((2-o^2)(3-o^2))/((1-o^2)o)], [o,0.01,0.99])$ 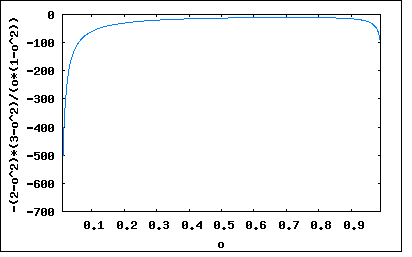という具合に一端はインピーダンス値が増加するものの途中で減少し-∞へ逆戻りしてしまう。こんな周波数特性をもった回路は受動素子だけでは実現できない。同じ式を部分分数に展開すると (%i19) (s^2+2)(s^2+3)/(s(s^2+1)); (%o19) ((s^2+2)(s^2+3))/(s(s^2+1)) (%i20) partfrac(((s^2+2)(s^2+3))/(s(s^2+1)), s); (%o20) -(2s)/(s^2+1)+s+6/s すなわち $\begin{array}{rcl}Z(s)&=&\frac{\left(s^2+2\right)\left(s^2+3\right)}{s \left(s^2+1\right)}\\&=&\frac{-(2s)}{(s^2+1)}+s+\frac{6}{s}\\&=&s(\frac{-2}{(s^2+1)}+1+\frac{6}{s^2})\end{array}$ ということになり、負の留数を持つためこれは正実関数ではないということになる。一方零点と極が交互に現れる以下のような関数では $Z(j\omega)=-j\frac{\left(1-\omega^2\right)\left(3-\omega^2\right)}{\omega \left(2-\omega^2\right)}$ ω=0からω=1.4の近傍をプロットしてみると、ω=1に零点が現れて極(ω=2)に向かって増加しているのがわかる。 wxplot2d([-((1-o^2)(3-o^2))/((2-o^2)o)], [o,0.1,1.4])$ 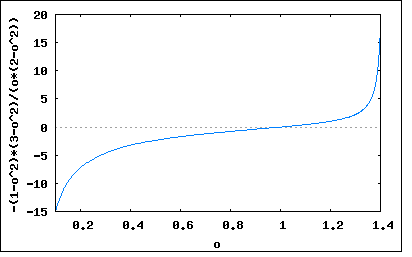同様に部分分数に展開してみると (%i21) partfrac(((s^2+1)(s^2+3))/(s(s^2+2)), s); (%o21) s/(2(s^2+2))+s+3/(2*s) すなわち $\begin{array}{rcl}Z(s)&=&\frac{\left(s^2+1\right)\left(s^2+3\right)}{s \left(s^2+2\right)}\\&=&\frac{s}{2(s^2+2)}+s+\frac{3}{2s}\\&=&s(\frac{0.5}{(s^2+2)}+1+\frac{1.5}{s^2})\end{array}$ 留数はすべて正の値をとるため正実関数である。この辺を厳密に数学的に説明もしくは証明するのは他書に譲るとして、ここでは定性的に零点と極は１位孤立で交互に現れなければ正実関数でないとする、すなわち $\leq\omega_1<\omega_2<...<\omega_{2n-2}<\omega_{2n-1}\leq\infty$ ということになる。ここで $0\leq\omega_1$ としたのはω=0を零点にもつケースを含むためである。同様に先ほど疑問の生じたω=∞の時にリアクタンス関数はどうなるかという点。 ω=0に極を持つケースでは、 $\begin{array}{rcl}\lim_{s\to\infty} Z(s) &=& \lim_{s\to\infty}H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}H\frac{\left(s^{2n}+a_{n-1}s^{2(n-1)}+...+a_{1}s^2+a_0\right)}{s \left(s^{2(n-1)}+b_{m-1}s^{2(n-2)}+...+b_{1}s^2+b_0\right)}\\ &=& \lim_{s\to\infty}H\frac{s^{2n}\left(1+a_{n-1}s^{-2}+...+a_{1}s^{-2(n-1)}+a_0{s^{-2n}}\right)}{s^{2(n-1)+1} \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \lim_{s\to\infty}s H\frac{\left(1+a_{n-1}s^{-2}+...+a_{1}s^{-2(n-1)}+a_0{s^{-2n}}\right)}{\left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \infty\end{array}$ ω=0に零点を持つケースでは、 $\begin{array}{rcl}\lim_{s\to\infty} Z(s) &=& \lim_{s\to\infty}s H \frac{\left(s^2+{\omega_{3}}^2\right)\left(s^2+{\omega_{5}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)\left(s^2+{\omega_{2n-1}}^2\right)}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}s H\frac{\left(s^{2(n-1)}+a_{n-2}s^{2(n-2)}+...+a_{1}s^2+a_0\right)}{\left(s^{2(n-1)}+b_{m-1}s^{2(n-2)}+...+b_{1}s^2+b_0\right)}\\ &=& \lim_{s\to\infty}s H\frac{s^{2(n-1)}\left(1+a_{n-2}s^{-2}+...+a_{1}s^{-2(n-2)}+a_0{s^{-2(n-1)}}\right)}{s^{2(n-1)} \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \lim_{s\to\infty}s H\frac{\left(1+a_{n-2}s^{-2}+...+a_{1}s^{-2(n-2)}+a_0{s^{-2(n-1)}}\right)}{\left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \infty\end{array}$ どちらのケースでも分子の次数が分母の次数より1大きいので、ω=∞ではZ=∞となる。従ってω=∞は極ということになる。しかし $\omega_{2n-1}\leq\infty$ としたように、もしω=∞を零点にもつようならば、ω=∞で分子は0に収束するためZ=0となり零点となる。このケースでは $(s^2+{\omega_{2n-1}}^2)$ の項を分子の式から取り除いて分子の次数を2減らし、分母の次数が分子の次数に比べ1大きくなったのと同じである。 ω=0を極としω=∞を零点とするケースでは、 $\begin{array}{rcl}\lim_{s\to\infty} Z(s) &=& \lim_{s\to\infty}H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)\cancel{\left(s^2+{\infty}^2\right)}}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}H\frac{\left(s^{2(n-1)}+a_{n-2}s^{2(n-2)}+...+a_{1}s^2+a_0\right)}{s \left(s^{2(n-1)}+b_{m-1}s^{2(n-2)}+...+b_{1}s^2+b_0\right)}\\ &=& \lim_{s\to\infty}H\frac{s^{2(n-1)}\left(1+a_{n-2}s^{-2}+...+a_{1}s^{-2(n-2)}+a_0{s^{-2(n-1)}}\right)}{s^{2(n-1)+1} \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \lim_{s\to\infty}H\frac{\left(1+a_{n-2}s^{-2}+...+a_{1}s^{-2(n-2)}+a_0{s^{-2(n-1)}}\right)}{s \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& 0\end{array}$ これがIQが低い者にとってはピンとこない。わかってしまえば、なんだあたりまえじゃないか(´∀` )という笑い話になるのだが。同様にω=0とω=∞の両方に零点を持つケースでは、 $\begin{array}{rcl}\lim_{s\to\infty} Z(s) &=& \lim_{s\to\infty}s H \frac{\left(s^2+{\omega_{3}}^2\right)\left(s^2+{\omega_{5}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)\cancel{\left(s^2+{\infty}^2\right)}}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}s H \frac{\left(s^2+{\omega_{3}}^2\right)\left(s^2+{\omega_{5}}^2\right)...\left(s^2+{\omega_{2n-3}}^2\right)}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ &=& \lim_{s\to\infty}s H\frac{\left(s^{2(n-2)}+a_{n-3}s^{2(n-3)}+...+a_{1}s^2+a_0\right)}{\left(s^{2(n-1)}+b_{m-1}s^{2(n-2)}+...+b_{1}s^2+b_0\right)}\\ &=& \lim_{s\to\infty}s H\frac{s^{2(n-2)}\left(1+a_{n-3}s^{-2}+...+a_{1}s^{-2(n-3)}+a_0{s^{-2(n-2)}}\right)}{s^{2(n-1)} \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& \lim_{s\to\infty}H\frac{\left(1+a_{n-3}s^{-2}+...+a_{1}s^{-2(n-3)}+a_0{s^{-2(n-2)}}\right)}{s \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\\ &=& 0\end{array}$ ということになる。これでようやく下記４つのケースに分かれることが納得いく。 $\begin{array}Case & \omega=0 & \omega=\infty\\ 1 & pole & pole \\ 2 & zero & zero \\ 3 & pole & zero \\ 4 & zero & pole\end{array}$ これで色々な本に書いてあることが理解できるようになった。いくらどの本にも同じことが書いてあっても、偉い先生が書いたものであっても、自分が納得いかない限り理解したとは言えないわけで。自分なりに納得がいく理解が得られれば、著者によっていろいろ表現や表記が違っていても同じことを書いているということをようやく理解できるわけである。IQが高い者なら一冊読むだけですべてを瞬時に理解してしまうかもしれないが、IQが低いものにとってはそれはそれは時間が必要である。誰か理解している人が側に入れば幸いかというとそうでもない。誰も教えてくれる人が居ない方が自ら切り開く力が備わるのである。先端に到達するともう後ろにも前にも自分よりも知っている人は誰もいなくなるわけで、そのときに自ら切り開く力が初めて問われる。さて話を本流に戻そう。まだ終わっていない。零点の近傍での虚軸に対する微係数が正であることを確かめなければならない。これには何度も登場する駆動点インピーダンス（リアクタンス関数）の式を部分分数に分解してωで微分してみる必要がある。当初それをやってみた結果を書いたのだが間違いに気づいてすぐ消してしまった。その間違いの原因を知るのに結構時間を要した。なにしろ多項式の有理関数の部分分数展開なんてのは、ヘビサイドが展開定理を発見するまで数学者は誰も知らなかったわけだし。まあ、多項式を多項式で割ると商と余りが出るのはみんな知っていたわけだけど、その余りの部分はヘビサイドが展開定理を見いだすまで余りのまま（多項式の有理式のまま）だった。そんなばかなと思うけど、それが歴史上の事実なのだ。ヘビサイドは数学的に証明したわけではなくそれを演算子法と併せて伝送路の過渡応答解析のための微分方程式を解くためにそれを用いた、それが厳密に数学で証明されるには後の群論とか抽象代数学の発達を待つ必要があった。べき級数の多項式の有理関数は、同一基数の数同志の割り算と同形であることに気づく必要がある。２端子回路（一端子対回路）に関する参考書はどれも最初に導出した駆動点インピーダンスの式が以下の様な部分分数に展開できるとしか書いていない。 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ 分数が理解できないわけではないが、最初に自分で駆動点インピーダンスの式を部分分数に展開しようと試みた際に過ちを侵した時に一連の疑問が生じた。手元の共立出版の「数学公式」には"8. 分数"の章に以下の様な部分分数展開の公式が載っている。引用： 8.4 部分分数　f(x)およびg(x)が実係数のxの整式で、g(x)の次数がf(x)の次数より低く、且つg(x)/f(x)が既約分数であるとする。f(x)が $f(x)=(x-\alpha)^k...(x-\beta)^l(x^2+px+q)^m...(x^2+rx+s)^n$ に分解されたとすれば $\frac{g(x)}{f(x)}=\frac{A_1}{(x-\alpha)^k}+\frac{A_2}{(x-\alpha)^{k-1}}+...+\frac{A_k}{x-\alpha}\\+...\\+\frac{B_1}{(x-\beta)^l}+\frac{B_2}{(x-\beta)^{l-1}}+...+\frac{B_l}{x-\beta}\\+...\\+\frac{C_1{x}+D_1}{(x^2+px+q)^m}+\frac{C_2{x}+D_2}{(x^2+px+q)^{m-1}}+...+\frac{C_m{x}+D_m}{x^2+px+q}\\+...\\+\frac{E_1{x}+F_1}{(x^2+rx+s)^n}+\frac{E_2{x}+F_2}{(x^2+rx+s)^{n-1}}+...+\frac{E_n{x}+F_n}{x^2+rx+s}$ ただしα,...,β,p,q,...,r,s及びA,B,C,D,E,Fは何れも実数で $p^2-4q<0,...,r^2-4s<0$ とする。これはまさにヘビサイドの展開定理そのものであるのだが、これに基づいて駆動点インピーダンスの式を部分分数展開しようとしたのが問題だった。良く見れば、この展開定理は分子の多項式の次数が分母の多項式の次数よりも低いことが前提である。今回の駆動点インピーダンスの式は分子の方が分母よりも次数が１つ高いので、そのまま使うと誤った結果を招いてしまう。それでは分子の次数が分母の次数よりも高い場合にはどうすればいいのか、公式集のその章にはそのケースについては書かれていない。では多項式の一般的な割り算（除法）はどうなっているのかというと、これはずっと後の"J. 整数論"という章に引用： 1.8 Euclidの互除法　aは任意の正または負の整数でbが正の整数ならば、 $a=qb+r, 0\leq{r}<b$ を満足する整数q,rは唯一通り存在する。と書いてあるだけである。所謂割り算の商(q)と余り(r)についての話であるが、部分分数展開の定理もEuclidの互除法に続いて書いてある以下の定理群から自明であるとも感じ取られる。引用： 1.9 a,bが互いに素なるとき 1. bcがaで整除されれば、cはaで整除される。 2. $a^m$ と $b^n$ とは互いに素である。 3. ax+by=1を満足するx,yが存在する。 4. a,2a,3a,...,(b-1)aをbで割った余りは互いに異なる数である。実は多項式と分数の関係は歴史が古く、数学史の中でも古代から存在しているのと、既に現在では"終わった"領域であるという点である。従って最も古い古典数学とも言える。しかし数学の発展上欠くことができないのは言うまでもない。多項式は方程式の解法という問題と密接に絡んでいるし、様々の基数の数の表現はまさに多項式そのものである。複素解析に至っては多公式の分数で表される有理型関数が重要な振る舞いをするのは回路網合成理論でも同じこと。なぜそれだけ重要な様々な分野で同時発生している数学的な対象がまともに関連づけて体系的に説明されていないのかが疑問として出てくる。数学は蟻の巣穴のようで様々な意図で別々の場所から掘り進んだ穴が偶然かもしくは起こるべくして起こるように一カ所でつながるということはあり得るが、およそ多項式と分数については、時空を通り越して別空間でまったく離れた場所でつながりあっているようにしか見えない。それを納得いくように理解するには自分で理論を再構成するしかない。実際にいろいろ調べてみると、部分分数展開については、やはりそれが登場する複素解析の有理型関数の積分のところで、著名なテキストではそれぞれ著者が独自に再構成した証明や導出手順を載せているのを見つけることができる。代数学では単に最新の抽象代数理論でEuclidの互除法の定義を再構成しているだけにすぎない。従って代数学の本を読んでもわからないわけである。手元にある「A COURSE OF MODERN ANALYSIS」では"5.64 Functions with the essential singularities"に、Liouville's Theoremによって孤立特異点を持つ有理型一変数複素関数が以下の式で表されることを導いている。 $f(z)=C+a_1{z}+a_2{z^2}+...+a_n{z^n}+\sum_{r=1}^k\left{\frac{a_{r,1}}{z-c_r}+\frac{a_{r,2}}{(z-c_r)^2}+...+\frac{a_{r,n_r}}{(z-c_r)^{n_r}}\right}$ また代数的整数論講義とかの著者で知られる高木貞治の「解析概論」の"66. 有理関数の積分の理論"でも独自の構成で有理関数 $f(z)=\frac{\phi(z)}{\psi(z)}$ がαをf(z)のk次の極であるとすると、f(z)の主要部が(z-α)^kf(z)のαにおけるTaylor展開の最初のk項 $a_k+a_{k-1}(z-\alpha)+...+a_1(z-\alpha)^{k-1}$ を(z-α)^kで割って $P(\alpha,z)=\frac{a_k}{(z-\alpha)^k}+...+\frac{a_1}{z-\alpha}$ が得られるのでφ(z)をψ(z)で割った商をQ(z)、剰余をφ0(z)とすれば $f(z)=Q(z)+\sum_{\alpha}P(\alpha,z)$ で表されることを示している。これらは同一の結論に至る、それぞれの著者が納得している解釈を示しているに過ぎず厳密な証明にはなっていない。おそらく自明だし、部分分数分解は数学的にも"終わった"話なのでこの程度の説明で十分だろうと思っている節がある。厳密な証明の形をした最も数学者的な部分分数展開の定義は共立出版から現在出版されている「代数方程式のガロア理論」"Galois'Theory of Algebraic Equation" Jean-Pierre Tignol著にある"第５章多項式の現代的解釈"の"付録：有理式の部分分数への分解"が最も厳密で現代的な形をしている。元々は大学生向けの講義内容であるが、代数方程式の歴史を紀元前2000年に既に分数を扱っていたバビロニア人の粘土板の記述からはじまる話は一般人にも面白く読める。インターネットでも分数で検索するとエジプト人が同様に分数を扱っていて建築物や構造物がすべて分数で表されることを知っていたらしいことがわかる。合理的な分数で表すことのできない不合理な無理数を発見した人物が謀殺された話とかは驚きである。これらを読んで、ようやく部分分数展開の定理がEuclidの互除法から導くことが出来るというのを確認した次第である。既に歴史上忘れ去られようとしているリアクタンス関数がこんなにも長い議論を招くとは思っても見なかったが、ようやくここまでたどり着いた感じがする。結論を言うと、最初侵した間違いというのは商を考えていなかったという点である。分子の次数が分母の次数より1高い場合には一次式が商として現れるのである。これが駆動点インピーダンスがω=∞で極を持つためには無くてはならない点だったということである。言うなれば常識なのだが。今の小学生は二学年で分数を習うらしい。昔は確か４学年と中途半端な時に習ったので、良く憶えていないし、学生になってからもちょっと自信が無かった憶えがある。分数はおそらく人類が暦や時間の概念を使い経済活動を始めたのと同時進行で考案された数学であると思われる。それだけに歴史が古い。数学専攻の学生は代数学でこうした古い数の概念を抽象理論で再構成しおさらいすることになるが、これがまた難しい。本当は小学二年生でそうした数への疑問を持てば、天才的な数学者が現れるかもしれないが、天下り的に教えるので、さっぱり憶えないという弊害があるかもしれない。やはり学ぶモチベーションを高めるのは自分が納得が行かない疑問を追求することが一番である。さてなんの話だったっけ。あ、そうだ駆動点インピーダンス関数の零点の近傍における微係数が正であることを証明しないといけない。そのために部分分数展開の話に迷い込んだのである。ここでようやく以下の様に展開された駆動点インピーダンスの式の導関数を求めることになる。 $\frac{dZ(s)}{ds}=\frac{d}{ds}(\frac{h_0}{s})+\frac{d}{ds}(\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2})+\frac{d}{ds}(h_\infty{s})\\=-\frac{h_0}{s^2}+\sum_{k=1}^n(\frac{h_{2k}}{s^2+{\omega_{2k}}^2}-\frac{2h_{2k}s^2}{(s^2+{\omega_{2k}}^2)^2})+h_\infty\\=-\frac{h_0}{s^2}+\sum_{k=1}^n\frac{h_{2k}(s^2+{\omega_{2k}}^2)-2h_{2k}s^2}{(s^2+{\omega_{2k}}^2)^2}+h_\infty\\=-\frac{h_0}{s^2}+\sum_{k=1}^n\frac{{\omega_{2k}}^2-s^2}{(s^2+{\omega_{2k}}^2)^2}h_{2k}+h_\infty$ ここでs=jωを代入すると $\frac{dZ(j\omega)}{d(j\omega)}=\frac{h_0}{\omega^2}+\sum_{k=1}^n\frac{{\omega_{2k}}^2+\omega^2}{({\omega_{2k}}^2-\omega^2)^2}h_{2k}+h_\infty\\=\frac{dZ(\omega)}{d(\omega)}>0$ であることが自明である。これらがFoster's Reactance Theoremである。著者はたった数行に要約しているだけだが、それだけではなんのことかさっぱりわからないのである。今日的にはこの理論はあまり活躍する機会が無い、というのも損失の無いLとCだけの回路というのが理想的すぎるので現実の素子の損失係数が無視できる低周波領域のみに適用範囲が絞られるのと、低周波領域では能動素子を使ったアクティブフィルタ回路かデジタル信号処理によるデジタルフィルタが今日の設計の主流であるためである、アナログフィルタの基礎を知るには後のCauerの損失を含む合成理論を学ぶ必要がある。今日でも高周波回路では未だに受動素子のみから成るフィルター回路が使われる。高周波のフロントエンドなど低損失かつ低ノイズが要求される部分は依然としてパッシブフィルタしか選択肢が無い。デジタルフィルタではサンプリング速度が追いつかないしノイズを発生する。マイクロ波とかではなおさらである。それでも基本の出発点はここにある。すっ飛ばして今日的なフィルタ理論とか先へ進んでも良いが、それらはFoster理論を理解していることを前提としているので、最後はここに戻って来ることになる。 P.S 賢明な読者であれば、複素解析理論の有理型関数の部分分数展開とヘビサイドの展開定理、それにFoster展開に関してmissing linkがあることに気づくであろう。Foster展開の分母が二次式である項は以下の様に共役複素数からなる２つの部分分数に更に分解されるはずである。この議論については次ぎのFoster展開で詳しく扱うことにする。 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\left{\frac{h_{2k}}{s+j{\omega_{2k}}}+\frac{h_{2k}\ast}{s-j{\omega_{2k}}}\right}+h_\infty{s}$

webadm	投稿日時: 2009-11-11 19:00
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	Foster展開（部分分数展開）さてこれまで二端子回路網の駆動点インピーダンスがLとCからのみ成る受動回路の場合に以下の様なリアクタンス関数として表されることと、現実に構成可能なための必要十分条件とそれらの諸性質について学んだ。 $Z(s)=H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ またそれらを部分分数に展開すると以下の様に表されることも学んだ。 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ これは良く見ると、以下の様に複数のインピーダンスの総和という形に捉え直すことができる。 $Z(s)=Z_0(s)+\sum_{k=1}^n Z_{2k}(s)+Z_\infty(s)$ ここで $Z_0(s)=\frac{h_0}{s}\\Z_{2k}(s)=\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}\\Z_\infty(s)=h_\infty{s}$ である。それぞれの部分インピーダンスの式にs=jωを代入して整理すると、 $Z_0(j\omega)=\frac{h_0}{j\omega}=\frac{1}{j\omega(\frac{1}{h_0})}=\frac{1}{j\omega C_0}\\Z_{2k}(j\omega)=\frac{h_{2k}j\omega}{(j\omega)^2+{\omega_{2k}}^2}=\frac{1}{j\omega(\frac{1}{h_{2k}})+\frac{1}{j\omega(\frac{h_{2k}}{{\omega_{2k}}^2})}}=\frac{1}{j\omega C_{2k}+\frac{1}{j\omega L_{2k}}}\\Z_\infty(j\omega)=h_\infty{j\omega}=j\omega h_\infty=j\omega L_\infty$ ここで $C_0=\frac{1}{h_0}\\L_{2k}=\frac{h_{2k}}{{\omega_{2k}}^2}\\C_{2k}=\frac{1}{h_{2k}}\\L_\infty=h_\infty$ ということになり、以下の図のような回路と等価であることがわかる。これをFoster第一形式と呼ぶ。一方、アドミッタンス関数として見ると $Y(s)=H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ リアクタンス関数と同様に部分分数展開され $Y(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ 以下のようなアドミッタンスの総和として表される $Y(s)=Y_0(s)+\sum_{k=1}^n Y_{2k}(s)+Y_\infty(s)$ ここで $Y_0(s)=\frac{h_0}{s}\\Y_{2k}(s)=\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}\\Y_\infty(s)=h_\infty{s}$ である。それぞれのアドミッタンスはs=jωに置き換えて整理すると $Y_0(j\omega)=\frac{h_0}{j\omega}=\frac{1}{j\omega(\frac{1}{h_0})}=\frac{1}{j\omega L_0}\\Y_{2k}(j\omega)=\frac{h_{2k}j\omega}{(j\omega)^2+{\omega_{2k}}^2}=\frac{1}{j\omega(\frac{1}{h_{2k}})+\frac{1}{j\omega(\frac{h_{2k}}{{\omega_{2k}}^2})}}=\frac{1}{j\omega L_{2k}+\frac{1}{j\omega C_{2k}}}\\Y_\infty(j\omega)=h_\infty{j\omega}=j\omega h_\infty=j\omega C_\infty$ ここで $L_0=\frac{1}{h_0}\\C_{2k}=\frac{h_{2k}}{{\omega_{2k}}^2}\\L_{2k}=\frac{1}{h_{2k}}\\C_\infty=h_\infty$ ということになり、以下の図のような回路と等価であることがわかる。これをFoster第二形式と呼ぶ。部分分数に展開した際の各係数を求めればそれらから等価回路の素子のインダクタンスやキャパシタンス値が得られることになる。それぞれの係数はリアクタンス関数の式が決まれば以下のようにして求まる。 ω=∞に極に持つケースでは $h_0=\left[s Z(s)\right]_{s=0}=\frac{H \omega_1^2\omega_3^2...}{\omega_2^2\omega_4^2...}\\h_{2k}=\left[\frac{\left(s^2+{\omega_{2k}}^2\right)}{s} Z(s)\right]_{s^2=-{\omega_{2k}}^2}=H\frac{({\omega_1}^2-{\omega_{2k}}^2)({\omega_3}^2-{\omega_{2k}}^2)...}{-{\omega_{2k}}^2({\omega_2}^2-{\omega_{2k}}^2)({\omega_4}^2-{\omega_{2k}}^2)...}\\h_\infty=\left[\frac{Z(s)}{s}\right]_{s=\infty}=\left[H\frac{\left(1+a_{n-1}s^{-2}+...+a_{1}s^{-2(n-1)}+a_0{s^{-2n}}\right)}{\left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\right]_{s=\infty}=H$ ω=∞を零点に持つケースでは $h_0=\left[s Z(s)\right]_{s=0}=\frac{H \omega_1^2\omega_3^2...}{\omega_2^2\omega_4^2...}\\h_{2k}=\left[\frac{\left(s^2+{\omega_{2k}}^2\right)}{s} Z(s)\right]_{s^2=-{\omega_{2k}}^2}=H\frac{({\omega_1}^2-{\omega_{2k}}^2)({\omega_3}^2-{\omega_{2k}}^2)...}{-{\omega_{2k}}^2({\omega_2}^2-{\omega_{2k}}^2)({\omega_4}^2-{\omega_{2k}}^2)...}\\h_\infty=\left[\frac{Z(s)}{s}\right]_{s=\infty}=\left[H\frac{\left(1+a_{n-1}s^{-2}+...+a_{1}s^{-2(n-1)}+a_0{s^{-2n}}\right)}{s \left(1+b_{m-1}s^{-2}+...+b_{1}s^{-2(n-2)}+b_0{s^{-2(n-1)}}\right)}\right]_{s=\infty}=0$ ということになりL∞は存在しないか短絡されたものと見なされる。上記はいずれもω=0に極を持つケースであるが、ω=0を零点とするケースでは、部分分数展開が以下の様になる。 $Z(s)=H \frac{\left(s^2+0\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\=s H \frac{\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\=\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ 従って直列のC0が存在しないか短絡された回路となる。これらのことから、Foster第一形式は以下の４ケースに分類される。 $\begin{array}Case & \omega=0 & \omega=\infty & C_0 & L_\infty\\ 1 & pole & pole & present & present\\ 2 & zero & zero & short-circuited & short-circuited\\ 3 & pole & zero & preset & short-circuited\\ 4 & zero & pole & short-circuited & presetnt\end{array}$ 同様のことがFoster第二形式についてもあてはまる。 $\begin{array}Case & \omega=0 & \omega=\infty & L_0 & C_\infty\\ 1 & pole & pole & present & present\\ 2 & zero & zero & absent & absent\\ 3 & pole & zero & preset & absent\\ 4 & zero & pole & absent & presetnt\end{array}$ また、Foster第一形式と第二形式は互いに逆の関係にあるので、同じ等価回路で一方が極をとるときその逆数は零点となり、その逆も真なりで、以下の対応関係が存在する。 $\begin{array}first Foster form & second Foster form\\ 1 & 2\\ 2 & 1\\ 3 & 4\\ 4 & 3\end{array}$ 等価回路を見れば、Foster第一形式から帯域阻止フィルタを、Foster第二形式から帯域通過フィルタを構成できることがわかる。逆数をとれば、それぞれ逆のフィルタにすることもできる。これはそれまで勘と経験のみに頼って設計されていた受動フィルタ回路が与えられた仕様から合成し解析できることを示した点で重要である。この業績は即座に当時米国に在住していた数学者Cauerの目にとまり、飛躍的な展開を見ることになる。ここで小休止して、リアクタンス関数の部分分数展開に関して、数学上とヘビサイドの展開定理との間にあるギャップを埋める考察をしておくことにしよう。気になって眠れないと困るので。数学的にはリアクタンス関数を有理型複素関数として部分分数展開すると、分母の式は互いに共役な虚根を持つため、数学上は以下の様に展開されるべきである。 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\left{\frac{h_{2k}}{s+j{\omega_{2k}}}+\frac{h_{2k}\ast}{s-j{\omega_{2k}}}\right}+h_\infty{s}$ ここでh2k,h2kは互いに共役な複素数ということになる。ヘビサイド演算子法を教えていた時代の古い電気回路の参考書には展開定理の生まれた経緯に関して "これは過渡現象を扱う場合に便利であるので付録として別に述べることにした。微分方程式の解法に用いられたのは1865年で、アイルランドのクイン大学(Queen's university)の数学者ブール(Boole)である。このときはd/dxの代わりにDを用いた。1881年のヘビサイド(Heaviside)の論文にこれがでている。彼はこれを積分定数の決定に用いた。1886年にはヘビサイドは共役定理(Conjugate theorem)を用い、その一ヶ月後に有名な展開定理(Expansion theorem)を完成している。" とかかれている。これと同じ趣旨のことは"Oliver Heaviside The life, work, and times of an electrical genius of the victorian age" Paul J. Nahin著にも書かれていて、ヘビサイドはBooleの著書を所有していたことは事実らしい。共役定理というのは何だ？　それが謎を解く鍵らしい。調べてみるとどうやら共役定理(conjugate theorem)というのは共役根定理(Conjugate pair theoremもしくはConjugate root theorem、あるいはまとめてComplex Conjugate Pair Root Theorem)と呼ばれているものらしい。n次の複素１変数代数方程式はn個の根を持つという代数学の基本定理の派生定理で、代数方程式が虚根を持つ場合、その共役もまた根であるというもの。つまり代数方程式の虚根はかならず互いに共役な対で存在するというもの。複素共役な部分分数に展開された項を再び結合すると $\frac{h_{2k}}{s+j{\omega_{2k}}}+\frac{h_{2k}\ast}{s-j{\omega_{2k}}}=\frac{h_{2k}(s-j{\omega_{2k}})+h_{2k}(s+j{\omega_{2k}}}{(s^2+{\omega_{2k}}^2)}=\frac{(h_{2k}+h_{2k})s+j(h_{2k}-h_{2k})\omega_{2k}}{(s^2+{\omega_{2k}}^2)}$ ということになる。ここで正実関数であるためには分子の多項式の係数がすべて正の実数でなければならないことから $h_{2k}-h_{2k}=0$ でなければならず従って h2k=h2k ということになる。先の部分分数展開は以下のように表すことができる。 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{2h_{2k}s}{(s^2+{\omega_{2k}}^2)}+h_\infty{s}$ 著書によっては、このように係数が2倍された表記が使用されているのはこのためである。

webadm	投稿日時: 2009-11-12 1:04
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	Cauer展開（連分数展開） Foster　reactance theoremに対する重要な進展が1927年ドイツ人Wilhelm Cauerによってもたらされた。彼は最初にリアクタンス関数を連分数展開することによって２つの異なる回路構成で表されることに気づいた。ところで連分数展開ってなんだ？複素解析の本には部分分数展開の話は出てくるが連分数展開の話はついぞ見かけない。連分数がどんなものかは憶えているが、連分数展開の方法については詳しく知らないのである。そもそも有理型多項式を連分数展開する方法は誰が考えたのだろうか？そして数学の歴史を知るためにまたしてもタイムマシンに乗らないといけないらしい。連分数は分数や多項式と同様に古くから研究されている数の表現方法である。すべて有理数は有限な連分数で表すことができる、無理数も無限の連分数で表すことができる。無理数を連分数で表すと、べき級数の多項式で表すよりも簡潔で規則性が現れるという不思議な事実も知られている。べき級数で表すと次数が高い項になるにつれ係数の分母や分子や乗数が大きな数となり情報量が増えてしまう。それに対して連分数で表すと、少ない数値と乗数だけで済む。実数をコンパクトに表現するには連分数の方が効率的らしい。コンピューターで使用されている浮動小数点表現はどうなのだろう？　あれは本当に効率的なのだろうか？すこしばかり数学の領域での連分数についておさらいしてみる必要がありそうである。有理型関数を連分数展開するには、部分分数展開と同じようにEuclidの互除法を使用する。 $Z(s)=\frac{N(s)}{D(s)}=Q_1(s)+\frac{R_1(s)}{D(s)}$ deg N(s) > deg D(s)の場合は上記の様に商Q1(s)と剰余R1(s)が得られる。当然deg R1(s) < deg D(s)なのであとは部分分数に展開するしかないと誰もが疑わなかった。Cauerはこれが以下の様に連分数に展開できることを示した。 $Z(s)=Q_1(s)+\frac{R_1(s)}{D(s)} \\ &=&Q_1(s)+\frac{1}{\frac{D(s)}{R_1(s)}} \\ &=&Q_1(s)+\frac{1}{Q_2(s)+\frac{R_2(s)}{D(s)}}\end{eqnarray}$ 剰余項の逆数の逆数は元と同じ、逆数にするとdeg D(s) > deg Rn(s)なので再び商と剰余が得られる。これを剰余が定数になるまで繰り返せばよい。 $Z(s)=Q_1(s)+\frac{1}{Q_2(s)+\frac{1}{Q_3(s)+\frac{1}{Q_4(s)+...}}$ さて次ぎにこの連分数展開の物理的な意味を議論する必要がある。 Z(s)がインピーダンス関数の場合は、Q1(s)はインピーダンスであり、残りの項もインピーダンスである。従って駆動点から見ると２つのインピーダンスが直列に接続されているように見える。最後のインピーダンスに関してその駆動点から見ると更に２つのアドミッタンスが並列に接続されているように見える。そして更に最後のアドミッタンスは連分数展開されて、２つのインピーダンスが直列に接続されているように見える。それを図に表すとこれを回路的に書き直すと、どっかで見たようなラダー回路を構成することが明らかとなる。これはFoster展開からは想像も出来なかったことである。これを再び駆動点インピーダンス関数の式として表すと $\begin{eqnarray}Z(s) &=&Z_1(s)+Z_2(s) \\ &=&Z_1(s)+\frac{1}{Y_2(s)+Y_3(s)} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+Z_4(s)}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+Y_5(s)}}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+\frac{1}{Z_5(s)+Z_6(s)}}}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+\frac{1}{Z_5(s)+\frac{1}{...}}}}}\end{eqnarray}$ ということになる。言われてみれば当たり前なのだが、直流回路理論を学んだ時にはこうした発想は思いもつかなかった。まさに数学と電気工学の境界領域に光を照らしたCauerならではである。これほどまでに数学の領域の有理型複素関数と物理的な電気回路の見事なまでの対称性は片方だけで食っていけた専門家には思いも寄らないことだったことが想像に難くない。ナチス一党独裁の下ユダヤ廃絶が極限に高まっていた当時、親戚にユダヤ系が一人居るということだけで教授の肩書きはあっても教職にはつけなけず、民間企業で食いつなぎ、ロックフェラー財団の招きでfellowとして米国に渡ってFosterなどベル研の研究者と出会うことができたのは不幸中の幸いだったのかもしれない。ドイツで何不自由のない教職生活が出来ていたなら我々が知るCauerは存在しなかったのかもしれない。ナチスを称賛するつもりは毛頭ないが、当時ナチスが存在しなければCauerの業績も無かったかもしれない。ナチスとCauerの理論は悪と善のような双対的存在として見ることもできるのはなんとも皮肉である。話をもとに戻そう。Cauer展開に関してもFoster展開と同様に駆動点インピーダンスの有理型関数をインピーダンス関数あるいはアドミッタンス関数として捉えるか、またそれぞれの極と零点の取り方に関する４つの組み合わせを考察する必要がある。それぞれについてどのような回路構成となるのか興味深いところである。再び駆動点インピーダンスの式 $Z(s)=H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ から出発することにしよう。これを部分分数に展開しても連分数に展開しても関数としての振る舞いはまったく同じでなければならない。元の駆動点インピーダンスの式は分子の次数が分母の次数よりも１大きいためs=jωと置いた時にω=0を零点、ω=∞に極を持つケースに該当する。実はここから連分数に展開するところで個人的に立ち止まってしまった。本書に限らずほとんどの書が最初にω=∞に極を持つ項を商として分離している。個人的にはもう一つの方法があると思ったのだ。これはFoster展開の式 $Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ を連分数展開に書き換える場合、以下の３通りがあると個人的に考えたのである。 $\begin{eqnarray}Z(s) &=&h_\infty{s}+Z_2(s) \\ Z(s) &=&\frac{h_0}{s}+Z_2(s) \\ Z(s) &=&\frac{h_{2}s}{s^2+{\omega_{2}}^2}+Z_2(s)\end{eqnarray}$ 本書に限らずどの本も最初の２つのみしか扱わず３番目は登場しない。とりあえず最初は伝統に従って最初の２つを扱い、最後に３番目を時間があれば考えてみることにしよう。 Cauer展開には有理型関数の連分数展開を考えないといけないのは当たり前なのだが、調べてみると連分数はやばい。嵌りそうでやばい。連分数というとRamanujan、Ramanujanというと連分数が出てくる。インド人の若き天才数学者Ramanujanと彼を発掘した英国Cambridge大の純粋数学者G.H.HardyはいずれもHeavisideやHeavisideの演算子法をラプラス変換とその逆変換(Bromwich積分）に対比させることによって皮肉にも演算子法の正しさを裏付けたBromwichと同時代に生きていた。Ramanujanについては最近多くのエピソードが満載の伝記小説が出版されている。日本の数学者の藤原氏の著書『天才の栄光と挫折―数学者列伝』にも登場する。個人的にはNHKの番組でその主題に基づくシリーズ講話が印象に残る。とにかく身近なテーマがなんでも公式が思いついてしまう魔術士のような天才だったらしい。近年まで彼が残した公式の証明が試みられていたらしい。それだけに連分数は生きた数学なのである。話をもとにもどそう。有理型関数の連分数展開を具体的にどうやるのか考える必要がある。公式集とかには連分数がどう表されるかは書いてあるが、どう分解するかは具体的な方法は書いていない。それだけに謎が多い。数学的には複素関数は零点と極によって特徴付けられるので、それがどのような形の式で表現されても同じなので部分分数展開も連分数展開も重要ではない。Riemannの時代にはまだ関数を式で表現することに意義を見いだしていた学派もあったが、それは式が零点と極を定めているのか、零点と極が式を決定付けているのかの違いでしかない。数学的にはどっちでも良い話だが、物理や工学では重要な意味を持つ。零点と極はリアクタンス回路網の仕様を決定するが、部分分数展開と連分数展開とで同じ回路網を実現するのに構成が異なるという点である。周波数や位相特性はどちらも同じであるにもかかわらずである。同じことが物理学にも言えて、質量や重力が空間を歪ませているのか、空間の歪みそのものが質量や重力を創り出しているのか、数学的にはどちらも同値だが、物理的には意味が異なる。式の表し方によって物理的に異なる構成をとるのであればこれまた悩ましい問題である。そんなこんなで連分数展開を考えている間に毎朝目の前の画面にいきなり公式が表示される夢で目が覚めるまでになってしまった。残念ながら夢の中ではスクリーンショットを取る暇はなかったので公式は憶えていない。ここ数日体調が悪くて寝込んでいた時も、胃腸の調子が悪くて意識混濁に陥っても頭の中では自分の体を一生懸命連分数展開しようとしていたのは内緒だ。さてそろそろ連分数展開を先に進めないといかん。連分数(continued fraction)も分数と同様に古くオイラー(Euler)やルジャンドル(Legendre)から研究され、多項式に関しても連分多項式(continuants)など数論にいくつかの重要な成果を残している。数論と言えば数学の女王と呼んだガウス(Gauss)も登場する。複素連分数に関してはフルビッツ(Hurwiz)や連分数解析理論の父と呼ばれるスチルチェス(Stieltjes)の名前が登場する。Hurwizは制御理論での安定性判定でも登場するので工学とのつながりは強い。StieltjesはRiemann-Stieltjes積分やLebesgue–Stieltjes積分の方が有名である。これらをまとめただけで一冊の本が出来るぐらいなのと、ほとんどは古典的な数論の範疇に留まっているため、目的とする多項式の連分数表現を数学的対象として扱うという試みは未踏の領域にあることだけがわかる。こうした理由から古い回路網理論の本では２端子回路についてFosterやCauerの例を扱っているが連分数展開に及んでは具体的な方法は省略されているか、あってもEuclidの互除法に従ってヒューリスティックな多項式の除算で剰余式を割り出していくという手順が示されているのが精一杯である。もっと見通しの良いアルゴリズムは無いのかというと今のところ平易なものは存在しないと言ったほうが正しいのかもしれない。近年に至ってはEuclidの互除法も連分数も学校では教えないことになっているので、自動的に連分数展開を伴うCauer展開を含む２端子回路そのものを教えないことになってしまっている。酷い本になると２端子回路はあるがFoster展開のみで終わっていて、Cauer展開は見事にスルーされているというものがあった。これなら２端子回路はやらないほうがまだましである。フィルタ理論にも２端子素子のラダー接続で構成された回路をCauerに敬意を表してCauerフィルタと呼ぶことが古い本では多かったが、最近ではCauerの業績が連分数展開というやっかいなものを伴うので講師から嫌われているのか、Cauerが先駆的な研究を行った楕円(Elliptic)フィルタもかつては敬意を表してCauerフィルタと呼ばれていた。現在はその元になっている関数の多項式近似理論の中のチェビシェフ近似多項式で知られるロシアの数学者チェビシェフ(Chebychev、Chebyshov、Tchebycheff、Tschebyscheffとか色々に転記されているが同一人物である）の名で呼ばれるようになってきている。今日アナログ回路設計者の多くがチェビシェフフィルタを考案したのはチェビシェフだというまったく誤った認識を持つに至っている。Cauerの名前は歴史から葬りさられようとしているのである。ナチスドイツの暗い時代を後生に伝えるのは良くないからだろうか。ちょっと残念である。チェビシェフ近似多項式を連分数展開すると切れ味の良い特性のフィルター回路が得られるのを発見したのはCauerなのである。フィルタ理論の本にもラダー構成(Cauer展開)のことをCauerトポロジーと書いてあるもののCauerの名前はそれしか出てこなかったりする。読者に質問されたら渋々答えるしかないのだろう。知って居る者にとってはCauerの名前を永遠に葬り去るのは忍びないに違いない。読者がCauerの事を詳しく知ろうとしてももうどこにも書いて無い、誰も知らないという時代がやってくるのはそう遠くはない気がする。みんな連分数が悪いのかもしれない（ちがう）。ということで連分数は数学的にもやっかいな代物で、数論でもEulerが扱ってしまったから触れないわけにはいかないけど、連分数をまったく知らなくても数論は体系的に理解可能というのが現実だ。連分数は未踏な領域につながっているので、深入りすると他が手につかなくなるので前途ある学生には教えない方が良いのかもしれない。そう考えることにしよう。というわけで長くなったが、代数学的に多項式の連分数展開（主に分子が常に1になる正則連分数展開）のいくつかのバリエーションを見通しの良い単一のアルゴリズムで扱う個人的な試みは一端は諦めざるを得ない。数学的な準備が全然足らないということを思い知ったからである。代数学の古本はいくつも買ってあるが、チンプンかんぷんで理解不能である。なんとなく出来そうな予想はあるが短期間に構成できそうなものではないので、古い回路網理論の本にあるようにヒューリスティックな多項式の割り算でお茶を濁すことにしよう。いつかはこの納得の行かない点を納得の行くアルゴリズムで見通しを良くすることは読者の課題としよう（振ってどうする）。そうすると後に学ぶフィルタ理論で埋めきれない大きな溝というか深い谷間が残ってしまう。いきなりラダー展開のフィルタ回路構成ばかりが登場するのである。それについてはその前に学ぶ２端子対回路が任意の２端子素子の結合で構成されるということを知ればフィルタ回路も２端子対回路でラダー構成も自明という理屈でごまかせるかもしれないが納得が行かない読者は少なからず居るだろう。誰が最初にラダー構成を思いついたのか、誰が最初に実用化したのか。そういう意味では思いついたのはCauerだが実用化したのはCauerではないので忘れられた存在になりつつあるのは致し方がないかもしれない。実務でのフィルタ回路は古くはAT&Tのベル研究所で多くの成果が成し遂げられているのでそちらに敬意を表するというのが当然かもしれない。Cauerは自分の特許をベル研にも売り込みに行っていてベル研の研究者も彼の存在を知ってはいたが、第二次世界大戦前にCauerは祖国ドイツに帰国したため米国の研究者は彼のことを後生に語り継げなかったに違いない。フィルタ回路理論から欠落してしまったCauerの理論は大きな深い谷間として残ることになる。なのでフィルタ回路の設計をしようとすると連分数展開でこの深い谷間を絶壁から覗き見することになる。これまでは一般的な有理型関数としてのリアクタンス関数を前提にしてきたが先の駆動点インピーダンスの式の逆数であるアドミッタンス式として連分数展開しようとすると、分母の次数が分子の次数よりも1大きいため商は無く剰余項だけとなる。 $Z(s)=\frac{1}{Y_2+\frac{1}{Z_3+\frac{1}{Y_4+\frac{1}{Z_5+...}}}}$ 従ってこれに対応する実際の回路構成はということになる。これもCauer展開である。。つまり商に対応する項が0なのでZ1項が存在しないか短絡された形になる。ここまでで連分数展開されたインピーダンスやアドミッタンス項がそれぞれどのような受動素子で構成されるのかは触れていなかったが、実際に回路合成する際には先に問題提起したようにインダクタンスなのかキャパシタンスなのかによって回路は２つの異なる構成を取ることになる。以下のように直列に接続されたインピーダンスがインダクタンスとして合成されたものを第一Cauer形と呼ぶ。それに対してキャパシタンスとして合成したものを第二Cauer型と呼ぶ。それぞれの形はω=0とω=∞に零点もしくは極のいずれかを持つかによって連分数展開の最初の項と最後の項が異なり、４つのケースが存在する。ここでは結果だけをまとめて表すことにする。第一Cauer形の場合 $\begin{array}Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\ 2 & zero & zero & C & L\\ 3 & pole & zero & C & C\\ 4 & zero & pole & L & L\end{array}$ 第二Cauer形の場合 $\begin{array}Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\ 2 & zero & zero & C & L\\ 3 & pole & zero & C & C\\ 4 & zero & pole & L & L\end{array}$ ということになる。一般的な回路網理論で扱われているのはここまでであるが、実際に電気回路設計に興味のある読者なら実際に設計してみたくなるかもしれない。その場合に以下の迷いが出てくる。 Foster展開とCauer展開のどちらが良いのか？　それぞれの第一形と第二形とどちらが良いのか？またどの回路構成にするか決めたものの実際に設計しようとすると仕様をちょっと変更する度にすべての計算をやり直さないといけなという煩雑なことになる。これを緩和するのために正規化した角周波数を用いて計算結果を表にしておけば、周波数が並行移動した場合でも設計計算は最小限ですむ方法が昔から用いられてきたのでそれについてもちょっと学んでおくことにしよう。はじめにω=0とω=∞とω=ω2に零点、ω1とω3に極を持つリアクタンス関数を考えてみよう。 $Z(s)=\frac{s(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)} \\ 0 < \omega_1 < \omega_2 < \omega_3 < \infty$ 分子の次数が分母の次数よりも1少ないのでこれは以下の様に部分分数展開することができる。 $\begin{eqnarray}&=&\frac{K_1 s}{(s^2+{\omega_1}^2)}+\frac{K_2 s}{(s^2+{\omega_3}^2)} \\ &=&\frac{1}{(\frac{1}{K_1}s+\frac{1}{\frac{K_1}{{\omega_1}^2}s})}+\frac{1}{(\frac{1}{K_2}s+\frac{1}{\frac{K_2}{{\omega_3}^2}s})} \\ &=&\frac{1}{(C_1 s+\frac{1}{L_1 s})}+\frac{1}{(C_2 s+\frac{1}{L_2 s})} \\ K_1 &=&\left.\frac{(s^2+{\omega_1}^2)}{s}(Z(s)-\frac{K_2 s}{(s^2+{\omega_3}^2)})\right\|_{s^2=-{\omega_1}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_1}^2)}}{\cancel{s}}\frac{\cancel{s}(s^2+{\omega_2}^2)}{\cancel{(s^2+{\omega_1}^2)}(s^2+{\omega_3}^2)}-\frac{(s^2+{\omega_1}^2)}{\cancel{s}}\frac{K_2 \cancel{s}}{(s^2+{\omega_3}^2)}\right\|_{s^2=-{\omega_1}^2} \\ &=&\frac{{\omega_2}^2-{\omega_1}^2}{{\omega_3}^2-{\omega_1}^2} \\ K_2 &=&\left.\frac{(s^2+{\omega_3}^2)}{s}(Z(s)-\frac{K_1 s}{(s^2+{\omega_1}^2)})\right\|_{s^2=-{\omega_3}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_3}^2)}}{\cancel{s}}\frac{\cancel{s}(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)\cancel{(s^2+{\omega_3}^2)}}-\frac{(s^2+{\omega_3}^2)}{\cancel{s}}\frac{K_1 \cancel{s}}{(s^2+{\omega_1}^2)}\right\|_{s^2=-{\omega_3}^2} \\ &=&\frac{{\omega_3}^2-{\omega_2}^2}{{\omega_3}^2-{\omega_1}^2} \\ C_1 &=&\frac{1}{K_1} \\ L_1 &=&\frac{K_1}{{\omega_1}^2} \\ C_2 &=&\frac{1}{K_2} \\ L_2 &=&\frac{K_2}{{\omega_3}^2}\end{eqnarray}$ これを第一Forster形でということになる。零点と極をとる角周波数をクリチカル周波数と呼び、そのうちω=0とω=∞は外部クリチカル周波数、それ以外を内部クリチカル周波数と呼ぶことにする。この場合、回路を構成するのに必要な素子数は内部クリチカル周波数（ω1,ω2,ω3)の数より常に１多いことが判る。また素子の定数が内部クリチカル周波数のみに依存することも重要な発見である。同じリアクタンス関数の逆数はアドミッタンス関数となり分子の次数が分母の次数より1大きくなるため部分分数展開すると商として一次式が切り出されることになる。 $\begin{eqnarray}Y(s)&=&\frac{1}{Z(s)}=\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s(s^2+{\omega_2}^2)} \\ &=&\frac{K_0}{s}+\frac{K_1 s}{(s^2+{\omega_2}^2)}+K_\infty s \\ &=&\frac{K_0}{s}+\frac{1}{(\frac{1}{K_1}s+\frac{1}{\frac{K_1}{{\omega_2}^2}s})}+K_\infty s \\ &=&\frac{1}{L_0 s}+\frac{1}{(L_1 s+\frac{1}{C_1 s})}+C_\infty s \\ K_0 &=&\left.s (Y(s)-\frac{K_1 s}{(s^2+{\omega_2}^2)}-K_\infty s)\right\|_{s=0} \\ &=&\left.\cancel{s}\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{\cancel{s}(s^2+{\omega_2}^2)}-\frac{K_1 s^2}{(s^2+{\omega_2}^2)}- K_\infty s^2\right\|_{s=0} \\ &=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2} \\ K_1 &=&\left.\frac{(s^2+{\omega_2}^2)}{s} (Y(s)-\frac{K_0}{s}-K_\infty s)\right\|_{s^2=-{\omega_2}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_2}^2)}(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s^2\cancel{(s^2+{\omega_2}^2)}}-\frac{(s^2+{\omega_2}^2)K_0}{s^2}-\frac{(s^2+{\omega_2}^2)}{\cancel{s}}K_\infty \cancel{s}\right\|_{s^2=-{\omega_2}^2} \\ &=&\frac{({\omega_2}^2-{\omega_1}^2)({\omega_3}^2-{\omega_2}^2)}{{\omega_2}^2} \\ K_\infty &=&\left.\frac{Y(s)-\frac{K_0}{s}-\frac{K_1 s}{(s^2+{\omega_2}^2)}}{s}\right\|_{s^2=\infty} \\ &=&\left.\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s^2(s^2+{\omega_2}^2)}-\frac{K_0}{s^2}-\frac{K_1}{(s^2+{\omega_2}^2)}\right\|_{s^2=\infty} \\ &=&\left.\frac{(1+\frac{{\omega_1}^2}{s^2})(1+\frac{{\omega_3}^2}{s^2})}{(1+\frac{{\omega_2}^2}{s^2})}\right\|_{s^2=\infty}=1 \\ L_0 &=&\frac{1}{K_0} \\ L_1 &=&\frac{1}{K_1} \\ C_1 &=&\frac{K_1}{{\omega_2}^2} \\ C_\infty &=&K_\infty\end{eqnarray}$ これを第二Foster展開でということになる。次ぎに同じリアクタンス関数をCauer展開（連分数展開）をしてみることにしよう。連分数展開するには先のリアクタンス関数の分子と分母をそれぞれ多項式に展開してEuclidの互除法を使ってヒューリスティックに式変形を行う必要がある。ずばり結論だけが得られる方法があればよいのだが今日の数学者の範疇外なので未踏のまま残されている。 $\begin{eqnarray}Z(s)&=&\frac{s(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)} \\ &=&\frac{s^3+{\omega_2}^2 s}{s^4+({\omega_1}^2+{\omega_3}^2) s^2+{\omega_1}^2{\omega_3}^2}\end{eqnarray}$ 分子の次数が分母の次数よりも１小さいので商が得られないため上の式そのものが剰余の式となる。連分数展開では剰余の逆数から商と剰余を切り出し、割り切れるか分子の式が定数になるまで繰り返すことになる。やってみると、 $\begin{array}{rrrrrrl}s^3+{\omega_2}^2 s ) & s^4 & + & ({\omega_1}^2+{\omega_3}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & ( s \\ & s^4 & + & {\omega_2}^2 s^2 & & & \\ \hline & & & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & \end{array}$ 従って $Z(s)=\frac{1}{s+\frac{({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2}{s^3+{\omega_2}^2 s}}$ ということになる。分母の式にまだ残っている剰余を更に連分数展開すると $\begin{array}{rrrrrrl}({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2 ) & s^3 & + & {\omega_2}^2 s & & & ( \frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s \\ & s^3 & + & \frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} s & & & \\ \hline & & & ({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s & & & \end{array}$ 従って $Z(s)=\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s}{({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2}}}$ ということになる。まだ有理型多項式の剰余が残っているので更に連分数展開すると $\begin{array}{rrrrrrl}({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s ) & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & & & ( \frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s \\ & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & & & & & \\ \hline & & & {\omega_1}^2{\omega_3}^2 & & & \end{array}$ 従って $\begin{eqnarray}Z(s)&=&\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s+\frac{{\omega_1}^2{\omega_3}^2}{({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s}}}} \\ &=&\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s+\frac{1}{\frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2}s}}}} \\ &=&\frac{1}{C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s+\frac{1}{L_5 s}}}} \\ C_2 &=& 1 \\ L_3 &=& \frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} \\ C_4 &=& \frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}} \\ L_5 &=& \frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2}\end{eqnarray}$ ということになる。これは第一Cauer形最後の第二Cauer形への展開だが、第二Foster形と同様にリアクタンス関数の逆数であるアドミッタンス関数として扱うのだが、予めsの逆数pでリアクタンス関数の式を書き直すと連分数展開が第一Cauer形と同じ要領でできることにようやく気づいた。これが長い間躓いていた原因だったのだが、これが変換群を成すという意味なのか。 $\begin{eqnarray}Y(s) &=&\frac{1}{Z(s)} \\ &=&\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s(s^2+{\omega_2}^2)} \\ &=&\frac{s^4+({\omega_1}^2+{\omega_3}^2) s^2+{\omega_1}^2{\omega_3}^2}{s^3+{\omega_2}^2 s} \\ &=&\frac{1+({\omega_1}^2+{\omega_3}^2) s^{-2}+{\omega_1}^2{\omega_3}^2 s^{-4}}{s^{-1}+{\omega_2}^2 s^{-3}} \\ &=&\frac{{\omega_1}^2{\omega_3}^2 s^{-4}+({\omega_1}^2+{\omega_3}^2) s^{-2}+1}{{\omega_2}^2 s^{-3}+s^{-1}} \\ &=&\frac{{\omega_1}^2{\omega_3}^2 p^{4}+({\omega_1}^2+{\omega_3}^2) p^{2}+1}{{\omega_2}^2 p^{3}+p} \\ p &=& s^{-1}\end{eqnarray}$ こうしておけば第一Cauer形と同様に連分数展開するだけである $\begin{array}{rrrrrrl}{\omega_2}^2 p^{3}+p ) & {\omega_1}^2{\omega_3}^2 p^{4} & + & ({\omega_1}^2+{\omega_3}^2) p^{2} & + & 1 & ( \frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p \\ & {\omega_1}^2{\omega_3}^2 p^{4} & + & \frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p^{2} & & & \\ \hline & & & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & + & 1 & \end{array}$ 従って $\begin{eqnarray}Y(s)=\frac{1}{Z(s)}&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1}{{\omega_2}^2 p^{3}+p}\end{eqnarray}$ 剰余項を更に同様に連分数展開すると $\begin{array}{rrrrrrl}({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1 ) & {\omega_2}^2 p^{3} & + & p & & & ( \frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p \\ & {\omega_2}^2 p^{3} & + & \frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p & & & \\ \hline & & & (1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p & & & \end{array}$ 従って $\begin{eqnarray}Y(s)&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p+\frac{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}{({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1}}\end{eqnarray}$ まだ剰余項が有理型多項式なので更に連分数展開すると $\begin{array}{rrrrrrl}(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p ) & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & + & 1 & & & ( \frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p \\ & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & & & & & \\ \hline & & & 1 & & & \end{array}$ 従って最終的には $\begin{eqnarray}Y(s)&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p+\frac{1}{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}}} \\ &=&\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2}}p+\frac{1}{\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2}}p+\frac{1}{\frac{1}{\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p+\frac{1}{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}}} \\ &=&\frac{1}{L_1 s}+\frac{1}{\frac{1}{C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}} \\ L_1 &=&\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2} \\ C_2 &=&\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2} \\ L_3 &=&\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}} \\ C_4 &=&\frac{1}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}} \end{eqnarray}$ これは第二Cauer形ということになる。ふう、計算が想像以上に面倒くさい。何度も間違いを犯したが、検証するにも複雑すぎる。実際にω1,ω2,ω3に適当に値を与えてグラフをプロットしてみることで確認してみよう。 ω1=10002π,ω2=15002π,ω3=20002πとして第一Foster形、第二Foster形、第一Cauer形、第二Cauer形のそれぞれの式に代入して素子の定数を求め回路シミュレーターで周波数特性をシミュレーションしてみよう。第一Foster形： $\begin{eqnarray}K_1 &=&\frac{{\omega_2}^2-{\omega_1}^2}{{\omega_3}^2-{\omega_1}^2} = \frac{{1500}^2-{1000}^2}{{2000}^2-{1000}^2} = \frac{5}{12}\\ K_2 &=&\frac{{\omega_3}^2-{\omega_2}^2}{{\omega_3}^2-{\omega_1}^2} = \frac{{2000}^2-{1500}^2}{{2000}^2-{1000}^2} = \frac{7}{12}\\ C_1 &=&\frac{1}{K_1} = \frac{12}{5} = 2.4 [F]\\ L_1 &=&\frac{K_1}{{\omega_1}^2} =\frac{\frac{5}{12}}{(1000\,2\pi)^2} = \frac{1}{9600000\,{\pi }^{2}} = 1.055\,10^{-8} [H]\\ C_2 &=&\frac{1}{K_2} = \frac{1}{\frac{7}{12}} = \frac{12}{7} = 1.714 [F]\\ L_2 &=&\frac{K_2}{{\omega_3}^2} = \frac{\frac{7}{12}}{(2000\,2\pi)^2} = \frac{7}{192000000\,{\pi }^{2}} = 3.694\,10^{-9} [H]\end{eqnarray}$ このリアクタンス関数の式では便宜上スケールファクタ(H)を1固定としているが実際にはスケールファクタを変えることによって素子の定数はより入手可能な範囲にすることができる。とりあえずこの定数で回路を組んで周波数特性を見てみると 1000Hz(ω1)と2000Hz(ω2)にピークが、1500Hz(ω2)にボトムが現れており意図したとおりの特性が出ていることが確認できた。同様に第二Foster型に関しても $\begin{eqnarray}K_0 &=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2} = \frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}=\frac{64000000\,{\pi }^{2}}{9}\\ K_1 &=&\frac{({\omega_2}^2-{\omega_1}^2)({\omega_3}^2-{\omega_2}^2)}{{\omega_2}^2} \\ &=&\frac{((1500\,2\pi)^2-(1000\,2\pi)^2)((2000\,2\pi)^2-(1500\,2\pi)^2)}{(1500\,2\pi)^2} =\frac{35000000\,\pi^2}{9}\\ K_\infty &=&1 \\ L_0 &=&\frac{1}{K_0} =\frac{9}{64000000\,{\pi }^{2}}=1.425\,{10}^{-8} [H]\\ L_1 &=&\frac{1}{K_1}=\frac{9}{35000000\,\pi^2}= 2.605\,10^{-8} [H]\\ C_1 &=&\frac{K_1}{{\omega_2}^2}=\frac{\frac{35000000\,\pi^2}{9}}{(1500\,2\pi)^2}= \frac{35}{81}=0.432 [F]\\ C_\infty &=&K_\infty=1 [F]\end{eqnarray}$ こちらも1000Hz,1500Hz,2000Hzにそれぞれピークが現れているので合っている。次ぎは第一Cauer形 $C_2 &=&1[F] \\ L_3 &=&\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} = \frac{1}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2} = \frac{1}{11000000\,{\pi }^{2}} = 9.211\,{10}^{-9}[H]\\ C_4 &=&\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}} = \frac{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}{(1500\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}} = \frac{121}{35} = 3.457[F] \\ L_5 &=&\frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2} = \frac{(1500\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}}{(1000\,2\pi)^2(2000\,2\pi)^2} = \frac{7}{140800000\,{\pi }^{2}} = 5.037\,{10}^{-9}[H]\end{eqnarray}$ これもどうやら合っているようだ。最後に第二Cauer形 $\begin{eqnarray}L_1 &=&\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2} = \frac{(1500\,2\pi)^2}{(1000\,2\pi)^2(2000\,2\pi)^2} = \frac{9}{64000000\,{\pi }^{2}} = 1.425\,{10}^{-8}[H]\\ C_2 &=&\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2} = \frac{(1000\,2\pi)^2+(2000\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}}{(1500\,2\pi)^2} = \frac{116}{81} = 1.432[F]\\ L_3 &=&\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}} = \frac{1-\frac{(1500\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}}}{(1000\,2\pi)^2+(2000\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}} = \frac{63}{2691200000\,{\pi }^{2}} = 2.372\,{10}^{-9}[H]\\ C_4 &=&\frac{1}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}} = \frac{1}{1-\frac{(1500\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}}} = \frac{116}{35} = 3.314[F]\end{eqnarray}$ こちらも同じ特性を持っていることが確認できた。もともとのリアクタンス関数の式がスケールファクタ(H)を1としているので現実的ではない大容量のキャパシタ定数になっているが、H=10^6とするとキャパシタンス定数はHで割り、インダクタンスはHを乗じれば良いので以下の様に現実的な定数の素子で同じ周波数特性(ただしインピーダンスはH倍になる）の回路が得られる。これらのことから仕様を満たす回路合成の可能性が見いだされたことは当時大きな驚きであったことは想像に難くない。それまでは試行錯誤で定数を見いだしていたのだから。受動素子のみからなる回路が今日あまり熱心に教えないのは以下の理由によるものであることはすぐに気づく・市販されている標準数列に基づいた定数の受動素子がほとんど利用できない・現実のインダクタンスは定数が大きくなればなるほど（巻き数が多いほど）漏洩キャパシタンスが多くなる・大容量のキャパシタンスやインダクタンスは容積が大きくかさばる・インダクタンスは隣接する他のインダクタンスと意図しない相互誘導を受ける・低インピーダンスな回路にしようとすると定数が更に非現実的となる（キャパシタンスはF単位と巨大にインダクタンスはnH単位と極端に微少になってしまう）・直流を素子する必要のある回路では周辺回路の直流阻止キャパシタ（ブロッキング・キャパシタ）を考慮して回路構成を決定する必要がある・現実の回路では２端子素子を複数組み合わせた入力端子と出力端子からなる２端子対回路を設計することが不可欠・理論を理解するのに複素解析の数学的前提知識が不可欠おそらく一端子対回路が学校で教えられなくなった背景にはこれらの理由が考えられる。中でも一番の理由は最後の複素解析の知識が必要であることが、高校卒者に電気回路理論を教えるのに大いなる妨げになるということがあるに違いない。日本の電気学会では唯一複素解析の知識が必要となる一端子対回路は早々と割愛してしまっている。ラプラス変換も複素積分の概念が理解には必要だが、それを知らなくても演算子法と同様に数式処理のテクニックとして詰め込むことは可能なので残っている。今日ではLとCだけからなる回路は高級なオーディオスピーカーユニット内部のネットワーク回路ぐらいだろう。話をもとにもどそう。最後にフィルタ設計で当たり前のように登場する正規化(Normalized)周波数について触れて終わりにしよう。それ以外にも周波数領域以外に位相特性はどうなるのかという疑問が湧くがそれは比較的自明なので読者の課題としよう。正規化周波数は特定の基準周波数（クリチカル周波数、アナログフィルタのカットオフ周波数や中心周波数、デジタルフィルタのナイキスト周波数など）を1として任意の周波数をそれとの比率で表したものである。これによって低周波から高周波まで極めて広範囲なレンジを持つ実際の周波数を用いることなく計算を容易にする。正規化周波数を用いて前述のFoster展開やCauer展開で定数を求めると正規化されたインダクタンスやキャパシタンスの値が得られることになる。実際の所望の周波数での定数を求めるにはこれらの正規化インダクタンスやキャパシタンスを所望の周波数で割れば済む。このように正規化周波数を使用して一度正規化された素子の定数を求めてしまえば、所望の周波数に基準周波数からシフトした場合の実際の定数は計算尺一つ（今は電卓か）で求めることができて設計がし易いということになる。任意の正規化（角）周波数(ω')と任意の角周波数(ω)と基準角周波数(ω0)との間では以下の関係が成り立つ $\begin{eqnarray}\omega'&=&\frac{\omega}{\omega_0} \\ \omega&=&\omega'\omega_0\end{eqnarray}$ これをs=jωとした駆動点インピーダンス関数の式に代入すると $\begin{eqnarray}Z(\omega)&=& -j H \frac{\left(-{\omega}^2+{\omega_{1}}^2\right)\left(-{\omega}^2+{\omega_{3}}^2\right)...\left(-{\omega}^2+{\omega_{2n-1}}^2\right)}{\omega \left(-{\omega}^2+{\omega_{2}}^2\right)\left(-{\omega}^2+{\omega_{4}}^2\right)...\left(^{\omega}^2+{\omega_{2n-2}}^2\right)} \\ Z(\omega')&=& -j H \frac{\left(-(\omega'\omega_0)^2+(\omega_{1}'\omega_0)^2\right)\left(-(\omega'\omega_0)^2+(\omega_{3}'\omega_0)^2\right)...\left(-(\omega'\omega_0)^2+(\omega_{2n-1}'\omega_0)^2\right)}{\omega'\omega_0 \left(-(\omega'\omega_0)^2+(\omega_{2}'\omega_0)^2\right)\left(-(\omega'\omega_0)^2+(\omega_{4}'\omega_0)^2\right)...\left(-(\omega'\omega_0)^2+(\omega_{2n-2}'\omega_0)^2\right)} \\ &=& -j H \frac{{\omega_0}^{2n}\left(-\omega'^2+\omega_{1}'^2\right)\left(-\omega'^2+\omega_{3}'^2\right)...\left(-\omega'^2+\omega_{2n-1}'^2\right)}{{\omega_0}^{2n-1} \omega' \left(-\omega'^2+\omega_{2}'^2\right)\left(-\omega'^2+\omega_{4}'^2\right)...\left(-\omega'^2+\omega_{2n-2}'^2\right)} \\ &=& -j H \frac{\omega_0 \left(-\omega'^2+\omega_{1}'^2\right)\left(-\omega'^2+\omega_{3}'^2\right)...\left(-\omega'^2+\omega_{2n-1}'^2\right)}{ \omega' \left(-\omega'^2+\omega_{2}'^2\right)\left(-\omega'^2+\omega_{4}'^2\right)...\left(-\omega'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}$ ということになる。今度は正規化複素周波数 $s'=j\omega'$ で置き換えると駆動点インピーダンスの式は ω=0とω=∞に極を持つケースで $\begin{eqnarray}Z(s')&=& H \omega_0 \frac{\left(s'^2+\omega_{1}'^2\right)\left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-1}'^2\right)}{ s' \left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}$ ということになる。同様にω=0に零点、ω=∞に極を持つケースでは $\begin{eqnarray}Z(s')&=& H \omega_0 \frac{s' \left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-1}'^2\right)}{\left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)} \end{eqnarray}$ ということになる。同様にω=∞に零点を持つ場合には分子の次数が分母の次数より1少なくなるのでそれぞれ ω=0に極、ω=∞に零点を持つケース $\begin{eqnarray}Z(s')&=& \frac{H}{\omega_0} \frac{\left(s'^2+\omega_{1}'^2\right)\left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-3}'^2\right)}{ s' \left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}$ ω=0とω=∞に零点を持つケース $\begin{eqnarray}Z(s')&=& \frac{H}{\omega_0} \frac{s' \left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-3}'^2\right)}{\left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}$ ということになる。実際に前出の第二Cauer展開を正規化周波数を用いて展開して整理みると $\begin{eqnarray}Y(s')&=&\frac{1}{L_1' s'}+\frac{1}{\frac{1}{C_2' s'}+\frac{1}{\frac{1}{L_3' s'}+C_4' s'}} \\ L_1' &=&\frac{1}{\omega_0}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} = \omega_0 L_1 \\ L_1 &=& \frac{L_1'}{\omega_0} \\ C_2' &=&\omega_0\frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} = \omega_0 C_2 \\ C_2 &=& \frac{C_2'}{\omega_0}\\ L_3' &=&\frac{1}{\omega_0}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}} = \omega_0 L_3 \\ L_3 &=& \frac{L_3'}{\omega_0} \\ C_4' &=&\omega_0 \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}} = \omega_0 C_4 \\ C_4 &=& \frac{C_4'}{\omega_0}\end{eqnarray}$ ということになる。また元の定数の式にω=ω'ω0を代入しても同じ結果が得られる。 $\begin{eqnarray}L_1 &=&\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2} = \frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2} = \frac{1}{\omega_0^2}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} = \frac{L_1'}{\omega_0} \\ L_1' &=&\frac{1}{\omega_0}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} \\ C_2 &=&\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2} = \frac{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}{(\omega_2'\omega_0)^2} = \frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} = \frac{C_2'}{\omega_0} \\ C_2' &=& \omega_0 \frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} \\ L_3 &=&\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}} = \frac{1-\frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}} = \frac{1}{\omega_0^2}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}} = \frac{L_3'}{\omega_0} \\ L_3' &=& \frac{1}{\omega_0}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}\\ C_4 &=&\frac{1}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}} = \frac{1}{1-\frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}} = \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}} = \frac{C_4'}{\omega_0} \\ C_4' &=& \omega_0 \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}\end{eqnarray}$ 従って正規化周波数で計算した値を所望の周波数で割れば所望のクリチカル周波数に特性をシフトした回路が得られることになる。実際にやってみると ω0=ω2=15002π(rad/sec) として正規化された素子定数を求めると $\begin{eqnarray}L_1' &=&\frac{1}{\omega_0}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} = \frac{1}{1500\,2\pi}\frac{{1}^2}{{\frac{2}{3}}^2{\frac{4}{3}}^2} = \frac{27}{64000\,\pi } \simeq 1.343\,{10}^{-4}\\ C_2' &=&\omega_0\frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} = 1500\,2\pi \frac{{\frac{2}{3}}^2+{\frac{4}{3}}^2-\frac{{\frac{2}{3}}^2{\frac{4}{3}}^2}{{1}^2}}{{1}^2} = \frac{116000\,\pi }{27} \simeq 13500 \\ L_3' &=&\frac{1}{\omega_0}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}} = \frac{1}{1500\,2\pi}\frac{1-\frac{{1}^2}{{\frac{2}{3}}^2+{\frac{4}{3}}^2-\frac{{\frac{2}{3}}^2{\frac{4}{3}}^2}{{1}^2}}}{{\frac{2}{3}}^2+{\frac{4}{3}}^2-\frac{{\frac{2}{3}}^2{\frac{4}{3}}^2}{{1}^2}} = \frac{189}{2691200\,\pi } \simeq 2.235\,{10}^{-5} \\ C_4' &=&\omega_0 \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}} = 1500\,2\pi \frac{1}{1-\frac{{1}^2}{{\frac{2}{3}}^2+{\frac{4}{3}}^2-\frac{{\frac{2}{3}}^2{\frac{4}{3}}^2}{{1}^2}}} = \frac{69600\,\pi }{7} \simeq 31240 \\ Z(s') &=&\frac{1}{\frac{1}{L_1' s'}+\frac{1}{\frac{1}{C_2' s'}+\frac{1}{\frac{1}{L_3' s'}+C_4' s'}}}=\frac{1}{\frac{1}{1.343\,{10}^{-4} s'}+\frac{1}{\frac{1}{13500 s'}+\frac{1}{\frac{1}{2.235\,{10}^{-5} s'}+31240 s'}}}\end{eqnarray}$ 正規化された駆動点インピーダンス関数の絶対値をプロットしてみると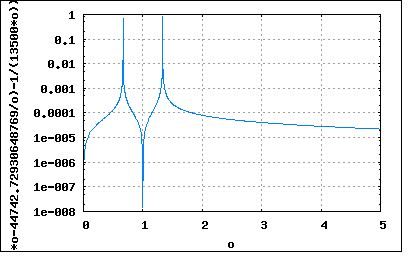確かにω2'=1(rad/sec)になっているのがわかる。今度はω0=4550002πとして中心周波数を455kHzにシフトした場合の定数を計算すると $\begin{eqnarray}L_1 &=&\frac{L_1'}{\omega_0} = \frac{1.343\,{10}^{-4}}{455000\,2\pi} = 4.698\,{10}^{-11}[H]\\ C_2 &=& \frac{C_2'}{\omega_0} = \frac{13500}{455000\,2\pi} = 0.004722 [F]\\ L_3 &=&\frac{L_3'}{\omega_0} = \frac{2.235\,{10}^{-5}}{455000\,2\pi} = 7.818\,{10}^{-12}[H]\\ C_4 &=&\frac{C_4'}{\omega_0} = \frac{31240}{455000\,2\pi} =0.01093 [F]\end{eqnarray}$ これらの定数に変えて回路シミュレータで周波数特性を測定すると見事に中心周波数ω0=ω2=455kHzにシフトしている。ω1とω3はそれぞれω2との元の比率を保っていることもわかる。これらの理論が考案された時代にはまだ電子計算機は利用できなかったので、もっぱら設計計算の現場では数値計算は計算尺が用いられていた。設計技術者はそれぞれ胸ポケットに必ず計算尺を忍び込ませていたものである。

webadm	投稿日時: 2009-12-2 4:14
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	RL一端子対回路ほとんどの回路網理論の著者はなんの脈略もなくLC一端子対回路に続いてRL一端子対回路やRC一端子対回路を説明している。このことが前にも述べたようにCauerを歴史から葬り去る傾向の現れでもある。我々はリアクタンス関数でやったようにCauerの再構成したやり方でRL,RC回路を扱うことにする。すなわち２種類の受動素子の組み合わせ(LC,RL,RC)からなるN端子網回路で一端子対以外の端子をすべて短絡したものを一端子対回路として出発する。この方法によってCauerはLC,RL,RC一端子対回路がすべて同型のaffine変換群であることを発見した。 The Scientific Work of Wilhelm Cauer and its Key Position at the Transition from Electrical Telegraph Techniques to Linear Systems Theory by Rainer Pauli このことについては数学的に高度すぎるので割愛されるのは仕方が無いが、中途半端にCauerの名前を出さずに結論だけ紹介するのは納得がいかない。リアクタンス関数で出てきた駆動点インピーダンスの定義に立ち戻ろう。 $Z=\frac{E_1}{I_1}=\frac{\Delta}{\Delta_{11}}$ $\Delta=\left\|\begin{matrix}Z_{11}&Z_{12}&Z_{13}&...&Z_{1n}\\Z_{21}&Z_{22}&Z_{23}&...&Z_{2n}\\.&.&.&&.\\.&.&.&&.\\.&.&.&&.\\Z_{n1}&Z_{n2}&Z_{n3}&...&Z_{nn}\end{matrix}\right\|$ リアクタンス関数の場合は損失の無いLとCからのみマトリックス要素Zijが構成されていたが、今度はRとLのみで構成されるので $\begin{eqnarray}Z_{ij}&=&s L_{ij}+R_{ij} \\ &=&L_{ij}(s+\frac{R_{ij}}{L_{ij}})\end{eqnarray}$ ということになる。ここで $\alpha_{ij}=\frac{R_{ij}}{L_{ij}}$ と置くと $Z_{ij}=L_{ij}\left(s+{\alpha_{ij}}\right)$ ということになる。従って $\begin{eqnarray}\Delta&=&Z_{11}Z_{22}...Z_{nn}+...\\&=&L_{11}\left(s+{\alpha_{11}}\right)L_{22}\left(s+{\alpha_{22}}\right)...L_{nn}\left(s+{\alpha_{nn}}\right)+...\\&=&a_n\left(s^{n}+a_{n-1}s^{n-1}+...+a_{1}s+a_0\right)\end{eqnarray}$ ここで $\Delta=0$ を満たすn個の根をそれぞれ $-{\alpha_1},-{\alpha_3},...,-{\alpha_{2n-1}}$ とすると $\Delta=a_n\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)$ 同様に $\begin{eqnarray}\Delta_{11}&=&Z_{22} Z_{33} ... Z_{nn}+...\\&=&L_{22}\left(s+{\alpha_{22}}\right) L_{33}\left(s+{\alpha_{33}}\right) ... L_{nn}\left(s+{\alpha_{nn}}\right)+...\\&=&b_m\left(s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0\right)\\&=&b_m\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)\end{eqnarray}$ 従ってRL一端子対回路の駆動点インピーダンスは $\begin{eqnarray}Z_{RL}(s)&=&\frac{a_n\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{b_m\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\&=&H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\ H > 0 && 0 \leq \alpha_1 < \alpha_2 < \alpha_3 <... <\alpha_{2n-2} < \alpha_{2n-1} < \infty \end{eqnarray}$ すべての根が実数であるため零点と極は負の実軸上にのみ現れる。これはsの実数部が負(Re(s)<0)の領域を意味し、振幅が時間と共に減衰して0に収束する場合に限られる。sの実数部が正の領域ではs=0を除いて零点も極も存在しないことを意味する。 LC一端子対回路と同様に分子の次数が分母の次数よりも1多い。LC一端子対回路の駆動点インピーダンスの式と見比べると $Z_{LC}(s)=H\frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ RL一端子対回路のsをs^2に置き換えsで割ったものと同型である。 $\begin{eqnarray}\frac{Z_{RL}(s^2)}{s}&=&Z_{LC}(s)\\ s Y_{RL}(s^2)&=&Y_{LC}(s)\end{eqnarray}$ また逆に $\begin{eqnarray}s Z_{LC}(s)&=&Z_{RL}(s^2)\\ \frac{Y_{LC}(s)}{s}&=&Y_{RL}(s^2)\end{eqnarray}$ ということになる。既にリアクタンス関数はsに関して奇関数であることを学んだので、上記の関係からRL一端子対回路の駆動点インピーダンスはs^2に関して偶関数であるということだけは言える。 RL一端子対回路の駆動点インピーダンスの式を部分分数展開すると分子の次数が分母の次数よりも1大きいので\|s\|=∞に極を持つため $\begin{eqnarray}Z_{RL}(s)&=&h_0+\sum_{k=1}^n\frac{h_{2k}s}{s+{\alpha_{2k}}}+h_\infty{s}$ ということになる。これは天下りなので何故こうなるのか納得がいかないので先へ進めなかった。前出のRL一端子対回路の式とLC一端子対回路の式の変換を使えば、LC一端子対回路の時の部分分数展開の式を変換することで上記の展開式を導くことが出来る、ということがようやく判った。リアクタンス関数の部分分数展開を思い出すと $Z_{LC}(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ 先ほどの関係式から、上記の式にsを乗じて、s^2をsに書き換えればRL一端子対回路の式となることから $s Z_{LC}(s)=s(\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}) = h_0+\sum_{k=1}^n\frac{h_{2k}s^2}{s^2+{\omega_{2k}}^2}+h_\infty{s^2} = Z_{RL}(s^2)$ 上記の式のs^2をsに、ω2k^2をα2kにそれぞれ置き換えればRL一端子対回路の式の部分分数展開となる $Z_{RL}(s)=h_0+\sum_{k=1}^n\frac{h_{2k}s}{s+{\alpha_{2k}}}+h_\infty{s}$ という種明かしだったのである。なんだ簡単じゃないか(´∀` ) これをFoster展開すると第一形では $\begin{eqnarray}Z_{RL}(s)&=&h_0+\sum_{k=1}^n\frac{1}{\frac{1}{h_{2k}}+\frac{{\alpha_{2k}}}{h_{2k}s}}+h_\infty{s}\\&=&R_{0}+\sum_{k=1}^n\frac{1}{G_{2k}+\frac{1}{L_{2k}s}}+L_{\infty}s\\R_{0}&=&h_0\\G_{2k}&=&\frac{1}{h_{2k}}\\L_{2k}&=&\frac{h_{2k}}{\alpha_{2k}}\\L_{\infty}&=&h_{\infty}\\h_0&=&\left[Z_{RL}(s)-\sum_{k=1}^n\frac{h_{2k}s}{s+{\alpha_{2k}}}-h_\infty{s}\right]_{s=0}\\&=&\left[H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\right]_{s=0}\\&=&H\frac{\alpha_{1}\alpha_{3}...\alpha_{2n-1}}{\alpha_{2}\alpha_{4}...\alpha_{2n-2}}\\h_{2k}&=&\left[\frac{s+\alpha_{2k}}{s}(Z_{RL}(s)-h_0-h_{\infty}s)\right]_{s=-\alpha_{2k}}\\&=&-H\frac{(\alpha_1-\alpha_{2k})(\alpha_3-\alpha_{2k})...(\alpha_{2n-1}-\alpha_{2k})}{\alpha_{2k}(\alpha_{2}-\alpha_{2k})(\alpha_{4}-\alpha_{2k})...(\alpha_{2k-2}-\alpha_{2k})(\alpha_{2k+2}-\alpha_{2k})...}\\h_{\infty}&=&\left[\frac{1}{s}(Z_{RL}(s)-h0-\sum_{k=1}^n\frac{h_{2k}s}{s+{\alpha_{2k}}})\right]_{s=\infty}\\&=&\left[H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\right]_{s=\infty}\\&=&\left[H \frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s(s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0)}\right]_{s=\infty}\\&=&\left[H \frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n}+b_{m-1}s^{n-1}+...+b_{1}s^2+b_0 s}\right]_{s=\infty}\\&=&\left[H \frac{1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0{s^{-n}}}{1+b_{m-1}s^{-1}+...+b_{1}s^{2-n}+b_0{s^{1-n}}}\right]_{s=\infty}=H\end{eqnarray}$ ということになり以下の様な回路構成となる。リアクタンス関数の時にやったように駆動点インピーダンス関数を駆動点アドミッタンス関数と見なすと $\begin{eqnarray}Y_{RL}(s)&=&h_0+\sum_{k=1}^n\frac{h_{2k}s}{s+{\alpha_{2k}}}+h_\infty{s}\\&=&G_{0}+\sum_{k=1}^n\frac{1}{R_{2k}+\frac{1}{C_{2k}s}}+C_{\infty}s\\G_{0}&=&h_0\\R_{2k}&=&\frac{1}{h_{2k}}\\C_{2k}&=&\frac{h_{2k}}{\omega_{2k}}\\C_{\infty}&=&h_{\infty}\end{eqnarray}$ む (つд⊂)ｺﾞｼｺﾞｼ Σ (ﾟДﾟ;）なんとアドミッタンス関数はRC回路になってしまった。回路構成で表すと。ということになる。これは原点に立ち戻って良く考えれば理由は明白である。最初にn端子対回路網のアドミッタンスマトリックスの全要素を $\begin{eqnarray}Y_{ij}&=&s C_{ij}+G_{ij} \\ &=&C_{ij}(s+\frac{G_{ij}}{C_{ij}})\end{eqnarray}$ として1端子対回路網の駆動点アドミッタンス関数を導いたことを意味し、LがCに変わってしまうためである。従ってRL一端子回路とRC一端子回路は双対的な関係にあると言える。LC一端子回路ではLとCがそれぞれCとLになってもLC一端子対回路であることには変わりなかったがRL一端子対回路やRC一端子対回路ではそうはならない。そこで改めて第一形でやったようにLC一端子対回路のアドミッタンス関数の部分分数展開式からRL一端子対回路のアドミッタンス関数の部分分数展開式を導いてみよう Foster展開（部分分数展開）で登場したLC一端子対回路のアドミッタンス関数の部分分数展開を再掲 $Y_{LC}(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}$ これをsで割って、s^2をsに変換すればRL一端子対回路の式になる $\frac{Y_{LC}(s)}{s}=\frac{1}{s}(\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s})=\frac{h_0}{s^2}+\sum_{k=1}^n\frac{h_{2k}}{s^2+{\omega_{2k}}^2}+h_\infty = Y_{RL}(s^2)$ 従ってs^2をsにω2k^2をα2kに置き換えると $Y_{RL}(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}}{s+{\alpha_{2k}}}+h_\infty$ ということになる。IQが低いとこういう数学的な発想は浮かばない。今度は最初の駆動点インピーダンス関数の逆数としての駆動点アドミッタンス関数を部分分数展開してみよう $\begin{eqnarray}Y_{RL}(s)&=&\frac{1}{Z_{RL}(s)}\\&=&\frac{1}{H} \frac{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}\\&=&\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k-1}}{s+{\alpha_{2k-1}}}+h_\infty\\ &=&\frac{1}{L_{0}s}+\sum_{k=1}^n\frac{1}{L_{2k-1}s+R_{2k-1}}+G_{\infty}\\L_{0}&=&\frac{1}{h_0}\\L_{2k-1}&=&\frac{1}{h_{2k-1}}\\R_{2k-1}&=&\frac{\alpha_{2k-1}}{h_{2k-1}}\\G_{\infty}&=&h_{\infty}\\h_0&=&\left[s (Y_{RL}(s)-\sum_{k=1}^n\frac{h_{2k-1}}{s+{\alpha_{2k-1}}}-h_\infty)\right]_{s=0}\\&=&\left[\frac{s}{H} \frac{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}\right]_{s=0}\\&=&0\\h_{2k-1}&=&\left[(s+\alpha_{2k-1})(Y_{RL}(s)-\frac{h_0}{s}-h_\infty)\right]_{s=-\alpha_{2k-1}}\\&=&\frac{1}{H}\frac{(\alpha_2-\alpha_{2k-1})(\alpha_4-\alpha_{2k-1})...(\alpha_{2n-2}-\alpha_{2k-1})}{(\alpha_{1}-\alpha_{2k-1})(\alpha_{3}-\alpha_{2k-1})...(\alpha_{2k-3}-\alpha_{2k-1})(\alpha_{2k+1}-\alpha_{2k-1})...}\\h_\infty&=&\left[Y_{RL}(s)-\frac{h_0}{s}-\sum_{k=1}^n\frac{h_{2k-1}}{s+{\omega_{2k-1}}}\right]_{s=\infty}\\&=&\left[\frac{1}{H} \frac{(s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0)}{(s^{n}+a_{n-2}s^{n-2}+...+a_{1}s+a_0)}\right]_{s=\infty}\\&=&\left[\frac{1}{H} \frac{(s^{-1}+b_{m-1}s^{-2}+...+b_{1}s^{1-n}+b_0 s^{-n})}{(1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0 s^{-n})}\right]_{s=\infty}\\&=&0\end{eqnarray}$ ということになる。良く見るL0とG∞の値は常に∞と0なのでアドミッタンスとして存在しないのと一緒である。分子の次数が分母の次数よりも1少ないので\|s\|=∞に零点を持つためG∞は存在せず、またs=0に零点を持たないのでL0も存在しないことになる。最初の頭の良い人向けの導き方ではなくて、普通の人向けの部分分数展開を考えれば以下のようになるはずである。 $\begin{eqnarray}Y_{RL}(s)&=&\frac{1}{H} \frac{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}\\&=&\sum_{k=1}^n\frac{h_{2k-1}}{s+{\alpha_{2k-1}}}\\&=&\sum_{k=1}^n\frac{1}{L_{2k-1}s+R_{2k-1}}\\L_{2k-1}&=&\frac{1}{h_{2k-1}}\\R_{2k-1}&=&\frac{\alpha_{2k-1}}{h_{2k-1}}\\h_{2k-1}&=&\left[(s+\alpha_{2k-1})Y_{RL}(s)\right]_{s=-\alpha_{2k-1}}\\&=&\frac{1}{H}\frac{(\alpha_2-\alpha_{2k-1})(\alpha-\alpha_{2k-1})...(\alpha_{2n-2}-\alpha_{2k-1})}{(\alpha_{1}-\alpha_{2k-1})(\alpha_{3}-\alpha_{2k-1})...(\alpha_{2k-3}-\alpha_{2k-1})(\alpha_{2k+1}-\alpha_{2k-1})...}\end{eqnarray}$ ということになるので元々L0,G∞は存在しないのである。一端子対回路についてページ数を多く割いている手元の古い本ではどれもL0,G∞の項は出てこない。割愛はしていないが要点のみに絞っている近年の本ではすべからくLC一端子対回路から変換したL0,G∞の項がある式が示されているのみで、実はそれらは存在しないというところまではページ数が割けず説明されていないので鵜呑みは禁物である。同様に第二形の駆動点インピーダンス式をそのまま駆動点インピーダンス関数とすると $\begin{eqnarray}Z_{RL}(s)&=&\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k-1}}{s+{\alpha_{2k-1}}}+h_\infty\\ &=&\frac{1}{C_{0}s}+\sum_{k=1}^n\frac{1}{C_{2k}s+G_{2k-1}}+R_{\infty}\\C_{0}&=&\frac{1}{h_0}\\C_{2k-1}&=&\frac{1}{h_{2k-1}}\\G_{2k-1}&=&\frac{\alpha_{2k-1}}{h_{2k-1}}\\R_{\infty}&=&h_{\infty}\end{eqnarray}$ ということになる。今度はCauer展開がどうなるか調べてみよう第一形では次数の大きい項から切り出していくのと分子の次数が分母の次数よりも1大きいのでsの一次式が最初に商として出てくる $\begin{eqnarray}Z_{RL}(s)&=&H(\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0})\\&=&L_{1}s+\frac{1}{G_2+\frac{1}{L_{3}s+\frac{1}{G_4+\frac{1}{L_{5}s+...}}}}\end{eqnarray}$ ということになる。第二形ではインピーダンス関数を最も次数の低い項から切り出していくので $\begin{eqnarray}Z_{RL}(s)&=&H(\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0})\\&=&H(\frac{1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0{s^{-n}}}{s^{-1}+b_{m-1}s^{-2}+...+b_{1}s^{1-n}+b_0{s^{-n}}})\\&=&H(\frac{1+a_{n-1}p+...+a_{1}p{n-1}+a_0{p^n}}{p+b_{m-1}p^{2}+...+b_{1}p^{n-1}+b_0{p^{n}}})\\&=&H(\frac{a_0{p^n}+a_{1}p{n-1}+...+a_{n-1}p+1}{b_0{p^{n}}+b_{1}p^{n-1}+...+b_{m-1}p^{2}+p})\\&=&R_{1}+\frac{1}{\frac{1}{L_{2}}p+\frac{1}{R_{3}+\frac{1}{\frac{1}{L_{4}}p+\frac{1}{R_{5}+...}}}}\\&=&R_{1}+\frac{1}{\frac{1}{L_{2}s}+\frac{1}{R_{3}+\frac{1}{\frac{1}{L_{4}s}+\frac{1}{R_{5}+...}}}}\\p&=&s^{-1}\end{eqnarray}$ ということになる。 Cauer展開でもFoster展開と同様にアドミッタンス関数として展開するとRC回路として合成される。第一形は次数の大きい項から切り出していくのと分子の次数が分母の次数より1大きいので $\begin{eqnarray}Y_{RL}(s)&=&H(\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0})\\&=&C_{1}s+\frac{1}{R_2+\frac{1}{C_{3}s+\frac{1}{R_4+\frac{1}{C_{5}s+...}}}}\end{eqnarray}$ 第二形は第一形と同じ式を次数の小さな項から切り出していくのと分子の次数が分母の次数よりも1大きいので $\begin{eqnarray}Y_{RL}(s)&=&H(\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0})\\&=&H(\frac{1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0{s^{-n}}}{s^{-1}+b_{m-1}s^{-2}+...+b_{1}s^{1-n}+b_0{s^{-n}}})\\&=&H(\frac{1+a_{n-1}p+...+a_{1}p{n-1}+a_0{p^n}}{p+b_{m-1}p^{2}+...+b_{1}p^{n-1}+b_0{p^{n}}})\\&=&H(\frac{a_0{p^n}+a_{1}p{n-1}+...+a_{n-1}p+1}{b_0{p^{n}}+b_{1}p^{n-1}+...+b_{m-1}p^{2}+p})\\&=&G_{1}+\frac{1}{\frac{1}{C_{2}}p+\frac{1}{G_{3}+\frac{1}{\frac{1}{C_{4}}p+\frac{1}{G_{5}+...}}}}\\&=&G_{1}+\frac{1}{\frac{1}{C_{2}s}+\frac{1}{G_{3}+\frac{1}{\frac{1}{C_{4}s}+\frac{1}{G_{5}+...}}}}\\p&=&s^{-1}\end{eqnarray}$ LC一端子対回路は零点と極が虚軸上にのみ現れるのに対して、RL一端子対回路の場合にはキャパシタンス素子が存在しない換わりに損失が存在するので共振点や逆共振点もなく零点と極は負の実軸上か\|s\|=∞にしか現れない点で性質が大きく異なる。一見すると同じ概念が通用しないように思えるが、数学的に見ると同じ変換群に属するということになる。というと難しいが、実はそうした高度な数学の話を持ち出さなくても平易な解説は出来るのを以下の本で知った電気書院　最新高級電験講座 4 「電気回路」大坪昭　著 RL一端子対回路のみならず一端子対回路は複素関数論を持ち出さなくても既に交流回路理論で学んだ記号法を使って平易に説明できることを示している。残念ながらページ数が割けない理由からか回路合成に関わる式が未知数である定数を左辺に置いたものではなく判り難いが間違ってはいない。定数を左辺に置くように書き換え整理するとここで書いたものと同じことが確認できる。ただ上記の本は電験受験者向けなのでそこに書いてある以上の理論的に未開拓な部分まで視野を広げることはしていない。そうした部分に興味のある人向けではない。数学の複素解析論を持ち出すことによって初めてその先まで視野を広げることができる。

webadm	投稿日時: 2009-12-20 2:36
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	Re: Cauer展開（連分数展開）このフォーラムでひとつの記事に含めることができる文字数に制限があるため、Cauer展開の後書き部分が欠落してしまうという事態が発生。そんなに長く書くもんじゃないらしい。消えてしまうのは忍びないので、幸いにしてGoogleキャッシュに残っていたものから救い出した後書き部分を掲載する。 P.S Cauerフィルタ理論とAT&Tベル研究所との歴史的な接点については"Design of Analog Filters" Rolf Schaumann, Mac E. Van Valkenburg著の"8.3 CAUER MAGNITUDE RESPONSE"に以下のように触れられている引用： Cauer first used his new theory in solving a filter problem for the German telephone industry. His new design achieved specifications with one less inductor than had ever been done before. The world first learned of the Cauer method not through scholarly publication but through a patent disclosure, which eventually reached the Bell Laboratories. Legend has it that the entire Mathmematics Department of Bell Laboratories spent the next 2 weeks at the New York Public Library studying elliptic functions. Cauer had studied mathematics under Hilbert at Göttingen, and so elliptic functions and their applications were familiar to him. Cauerは当初自身の新理論をドイツの電話会社でのフィルタ問題の解決に用いた。彼の新設計はそれ以前のものに比べインダクタがひとつ少ない仕様を実現した。Cauerの理論が世界で初めて明らかにされたのは論文ではなく特許開示によるもので、遂にベル研の知るところとなった。伝えられるところによると、ベル研の数学研究部門総員その後２週間ニューヨーク図書館に籠もって楕円関数の勉強に費やしたとか。Cauerはゲッチンゲン大学でHilbertの下で数学を研究してきたので楕円関数とその応用に関してはお手の物だったのである。 Mac E. Van Valkenburg氏は1955年に"NETWORK ANALYSIS"という本を出版している。偶然にもこの古本が手元にあり今回の一端子対回路に関してほとんどの構想を拝借する形で参考にさせて頂いている。興味深いことに執筆時点でFoster氏はまだご存命だったと思われ、引用： Reactance functions of the type studied in the chapter thus far were first investigated in 1924 by R. M. Foster, then of the Bell Telephone Laboratories but now at Brooklyn Polytechnic Institute. 本章で学んだタイプのリアクタンス関数は初めてR. M. Fosterによって1924年にベル研において突き止められたが、現在はBrooklyn Polytechnic Instituteに在籍。こうした先駆者の功績を折に触れ伝えることは今では希である。おそらく先に取り上げた興味深いエピソードも氏の文章だと思われる。当時はドイツ語原文でしか出版されていなかったCauerの遺稿を元に出版された著書も1958年に英文訳が出版されるに至っているが、未だに入手困難である。こうしたことが益々Cauerの功績が忘れられる理由かもしれない。

webadm	投稿日時: 2009-12-24 19:18
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	RC一端子対回路 RL一端子対回路の議論の中で、双対的な関係としてRC一端子回路が存在することが判ってしまったが、これまで所々で見え隠れしたLC一端子対回路とRL一端子対回路それにRC一端子対回路を対比しながらまとめて見ることにする。駆動点インピーダンスの一般式を導く際にn端子対回路のインピーダンスマトリックスの要素はRC一端子対回路では以下の様になる。 $\begin{eqnarray}Z_{ij}&=&R_{ij}+\frac{1}{C_{ij}s} \\ &=&\frac{R_{ij}}{s}(s+\frac{1}{C_{ij}R_{ij}})\end{eqnarray}$ これまでのLC,RLの場合と比較するために一覧表にすると $\begin{array}{\|c\|c\|}\hline Network & Z_{ij}\\ \hline LC & \frac{L_{ij}}{s}(s^2+\frac{1}{C_{ij}L_{ij}})\\ \hline RL & L_{ij}(s+\frac{R_{ij}}{L_{ij}})\\ \hline RC & \frac{R_{ij}}{s}(s+\frac{1}{C_{ij}R_{ij}}) \\ \hline\end{array}$ ということになる。ここで $\alpha_{ij}=\frac{1}{C_{ij}R_{ij}}$ と置くと $Z_{ij}=\frac{R_{ij}}{s}\left(s+{\alpha_{ij}}\right)$ ということになる。従って $\begin{eqnarray}\Delta&=&Z_{11}Z_{22}...Z_{nn}+...\\&=&\frac{R_{11}}{s}\left(s+{\alpha_{11}}\right)\frac{R_{22}}{s}\left(s+{\alpha_{22}}\right)...\frac{R_{nn}}{s}\left(s+{\alpha_{nn}}\right)+...\\&=&\frac{a_n}{s^n}\left(s^{n}+a_{n-1}s^{n-1}+...+a_{1}s+a_0\right)\end{eqnarray}$ ここで $\Delta=0$ を満たすn個の根をそれぞれ $-{\alpha_1},-{\alpha_3},...,-{\alpha_{2n-1}}$ とすると $\Delta=\frac{a_n}{s^n}\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)$ 同様に $\begin{eqnarray}\Delta_{11}&=&Z_{22} Z_{33} ... Z_{nn}+...\\&=&\frac{R_{22}}{s}\left(s+{\alpha_{22}}\right) \frac{R_{33}}{s}\left(s+{\alpha_{33}}\right) ... \frac{R_{nn}}{s}\left(s+{\alpha_{nn}}\right)+...\\&=&\frac{b_m}{s^{n-1}}\left(s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0\right)\\&=&\frac{b_m}{s^{n-1}}\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)\end{eqnarray}$ 従ってRC一端子対回路の駆動点インピーダンスは $\begin{eqnarray}Z_{RC}(s)&=&\frac{\frac{a_n}{s^n}\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{\frac{b_m}{s^{n-1}}\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\&=&H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s \left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\ H > 0 && 0 \leq \alpha_1 < \alpha_2 < \alpha_3 <... <\alpha_{2n-2} < \alpha_{2n-1} < \infty \end{eqnarray}$ 分子と分母の次数が同じである。s=0に必ず極を持ち、\|s\|=∞は零点でも極にもならない。他の極と零点は負の実軸上にのみ現れることがわかる。 LC一端子対回路の駆動点インピーダンスの式と見比べると $Z_{LC}(s)=H\frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}$ RC一端子対回路のsをs^2に置き換えてsを乗じるとLC一端子回路の式と同じになる。 $\begin{eqnarray}s Z_{RC}(s^2)&=&Z_{LC}(s)\\ \frac{Y_{RC}(s^2)}{s}&=& Y_{LC}(s)\end{eqnarray}$ または $\begin{eqnarray}\frac{Z_{LC}(s)}{s}&=&Z_{RC}(s^2)\\ s Y_{LC}(s)&=&Y_{RC}(s^2)\end{eqnarray}$ ということになる。 RC一端子対回路はRL一端子回路と同様に駆動点インピーダンス関数がs^2に関して偶関数ということになる。一覧表にして表すと $\begin{array}{\|c\|c\|}\hline Network & Z\\ \hline LC & H\frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s\left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}\\ \hline RL & H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\ \hline RC & H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s \left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\ \hline\end{array}$ ということになる。 RC一端子対回路の駆動点インピーダンス関数の部分分数展開は分子と分母の次数が同一なので定数項が商として切り出される、残りの剰余は分子の次数が分母の次数より少ないので展開定理を使用して $Z_{RC}(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}}{s+{\alpha_{2k}}}+h_\infty$ ということになる。 Foster展開すると $\begin{eqnarray}Z_{RC}(s)&=&\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}}{s+{\alpha_{2k}}}+h_\infty\\&=&\frac{1}{C_{0}s}+\sum_{k=1}^n\frac{1}{C_{2k}s+G_{2k}}+R_{\infty}\\C_{0}&=&\frac{1}{h_0}\\C_{2k}&=&\frac{1}{h_{2k}}\\G_{2k}&=&\frac{\alpha_{2k}}{h_{2k}}\\R_{\infty}&=&h_{\infty}\\h_0&=&\left[s(Z_{RC}(s)-\sum_{k=1}^n\frac{h_{2k}}{s+{\alpha_{2k}}}-h_\infty)\right]_{s=0}\\&=&\left[H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\right]_{s=0}\\&=&H\frac{\alpha_{1}\alpha_{3}...\alpha_{2n-1}}{\alpha_{2}\alpha_{4}...\alpha_{2n-2}}\\h_{2k}&=&\left[(s+\alpha_{2k})(Z_{RC}(s)-\frac{h_0}{s}-h_{\infty})\right]_{s=-\alpha_{2k}}\\&=&-H\frac{(\alpha_1-\alpha_{2k})(\alpha_3-\alpha_{2k})...(\alpha_{2n-1}-\alpha_{2k})}{\alpha_{2k}(\alpha_{2}-\alpha_{2k})(\alpha_{4}-\alpha_{2k})...(\alpha_{2k-2}-\alpha_{2k})(\alpha_{2k+2}-\alpha_{2k})...}\\h_{\infty}&=&\left[Z_{RC}(s)-\frac{h0}{s}-\sum_{k=1}^n\frac{h_{2k}}{s+{\alpha_{2k}}}\right]_{s=\infty}\\&=&\left[H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\right]_{s=\infty}\\&=&\left[H \frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s(s^{n-1}+b_{m-1}s^{n-2}+...+b_{1}s+b_0)}\right]_{s=\infty}\\&=&\left[H \frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n}+b_{m-1}s^{n-1}+...+b_{1}s^2+b_0 s}\right]_{s=\infty}\\&=&\left[H \frac{1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0{s^{-n}}}{1+b_{m-1}s^{-1}+...+b_{1}s^{2-n}+b_0{s^{1-n}}}\right]_{s=\infty}=H\end{eqnarray}$ ということになる。これはRL一端子対回路の駆動点アドミッタンス関数をそのまま駆動点インピーダンス関数とみなすと出てきたのと同じ回路である。今度は最初の駆動点インピーダンス関数の逆数としての駆動点アドミッタンス関数を部分分数展開してみよう $\begin{eqnarray}Y_{RC}(s)&=&\frac{1}{Z_{RC}(s)}\\&=&\frac{s}{H} \frac{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}\\&=&s(\frac{1}{H} \frac{\left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)})\\&=&s(\sum_{k=1}^n\frac{h_{2k-1}}{s+{\alpha_{2k-1}}})\\&=&\sum_{k=1}^n\frac{h_{2k-1}s}{s+{\alpha_{2k-1}}}\\ &=&\sum_{k=1}^n\frac{1}{\frac{1}{C_{2k-1}s}+R_{2k-1}}\\C_{2k-1}&=&\frac{h_{2k-1}}{\alpha_{2k-1}}\\R_{2k-1}&=&\frac{1}{h_{2k-1}}\\h_{2k-1}&=&\left[\frac{(s+\alpha_{2k-1})}{s}(Y_{RC}(s)-{h_0}-h_\infty{s})\right]_{s=-\alpha_{2k-1}}\\&=&\frac{1}{H}\frac{(\alpha_2-\alpha_{2k-1})(\alpha_4-\alpha_{2k-1})...(\alpha_{2n-2}-\alpha_{2k-1})}{(\alpha_{1}-\alpha_{2k-1})(\alpha_{3}-\alpha_{2k-1})...(\alpha_{2k-3}-\alpha_{2k-1})(\alpha_{2k+1}-\alpha_{2k-1})...}\end{eqnarray}$ 次ぎに駆動点インピーダンス関数のCauer展開がどうなるか見てみよう。第一形では次数の大きい項から切り出していく。 $\begin{eqnarray}Z_{RC}(s)&=&H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s \left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\&=&H\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n}+b_{m-1}s^{n-1}+...+b_{1}s^2+b_0 s}\\&=&R_{1}+\frac{1}{C_{2}s+\frac{1}{R_{3}+\frac{1}{C_{4}s+\frac{1}{R_{5}+...}}}}\end{eqnarray}$ 第二形ではインピーダンス関数を最も次数の低い項から切り出していくので $\begin{eqnarray}Z_{RC}(s)&=&H \frac{\left(s+{\alpha_{1}}\right)\left(s+{\alpha_{3}}\right)...\left(s+{\alpha_{2n-1}}\right)}{s \left(s+{\alpha_{2}}\right)\left(s+{\alpha_{4}}\right)...\left(s+{\alpha_{2n-2}}\right)}\\&=&H(\frac{s^n+a_{n-1}s^{n-1}+...+a_{1}s+a_0}{s^{n}+b_{m-1}s^{n-1}+...+b_{1}s+b_0 s})\\&=&H(\frac{1+a_{n-1}s^{-1}+...+a_{1}s^{1-n}+a_0{s^{-n}}}{1+b_{m-1}s^{-1}+...+b_{1}s^{2-n}+b_0{s^{1-n}}})\\&=&H(\frac{1+a_{n-1}p+...+a_{1}p{n-1}+a_0{p^n}}{1+b_{m-1}p+...+b_{1}p^{n-2}+b_0{p^{n-1}}})\\&=&H(\frac{a_0{p^n}+a_{1}p{n-1}+...+a_{n-1}p+1}{b_0{p^{n-1}}+b_{1}p^{n-2}+...+b_{m-1}p+1})\\&=&\frac{1}{C_{1}}p+\frac{1}{G_{2}+\frac{1}{\frac{1}{C_{3}}p+\frac{1}{G_{4}+\frac{1}{\frac{1}{C_{5}}p+...}}}}\\&=&\frac{1}{C_{1}s}+\frac{1}{G_{2}+\frac{1}{\frac{1}{C_{3}s}+\frac{1}{G_{4}+\frac{1}{\frac{1}{C_{5}s}+...}}}}\\p&=&s^{-1}\end{eqnarray}$ 今度は駆動点インピーダンス関数の逆数としてのアドミッタンス関数をCauer展開した場合どうなるか見てみよう。分子と分母の次数が同じなのでインピーダンスの場合と同様に連分数展開する方法でも同じ結果が得られるが式の逆数とした方が簡単である。 $\begin{eqnarray}Y_{RC}(s)&=&\frac{1}{Z_{RC}(s)}\\&=&\frac{1}{R_{1}+\frac{1}{C_{2}s+\frac{1}{R_{3}+\frac{1}{C_{4}s+\frac{1}{R_{5}+...}}}}}\end{eqnarray}$ 最初の素子が並列接続のR1でキャパシタンスが直列、抵抗が並列に生成される。今度は第二形次数の低い項から連分数展開しても同じ結果は得られるがちょっと面倒なのでインピーダンスの式の第二形の逆数をとるのが簡単 $\begin{eqnarray}Y_{RC}(s)&=&\frac{1}{Z_{RC}(s)}\\&=&\frac{1}{\frac{1}{C_{1}s}+\frac{1}{G_{2}+\frac{1}{\frac{1}{C_{3}s}+\frac{1}{G_{4}+\frac{1}{\frac{1}{C_{5}s}+...}}}}}\end{eqnarray}$ 最初の素子が並列C1で抵抗が直列にキャパシタが並列接続される。勘違いしやすくて最後まで嵌った。 RL一端子対回路の時には上の２ケースはやらなかったが、逆数の式を考えれば良いだけなので読者の課題としよう(´∀` )

(1) 2 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を