Gan's blog - フォーラム

(1) 2 »

投稿者	スレッド
webadm	投稿日時: 2010-5-4 1:49
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	二端子対回路ようやく二端子対回路まで進んだ。もともと電気回路理論を学ぼうとした発端は、トランジスタが縦列接続された回路の解析方法を分からずそれを知ろうとしたからだった。しかしここにきてその願いがかなうのはまだずっと先のことだということがようやく分かってきた。それはそれでひとつの到達点である。なんでも始めてみたら、目標としていた地点はまだずっと先だったというのは登山とか冒険、研究開発でよくあること。これから学ぶことになる二端子対回路は、トランジスタのような能動素子はもちろん、ダイオードのような非線形素子は無論、電源すらも含まない、受動素子からのみなる回路網が前提条件である。かなり制約があるが、実務的には後に学ぶ分布定数回路なども扱えるため受動素子からのみ成るフィルタや高周波伝送路などの伝送回路を扱うのに役立つ。ひとつ前の一端子対回路で駆動点インピーダンス関数についていろいろ基本を学んだことが役立つ。一般的に二端子対回路では与えられた条件での回路解析が主で、その合成は扱わない。というのも既に一端子対回路の演習問題で判ったように、回路の駆動点インピーダンス関数が得られたとしてもそれを実現する回路はひとつとは限らないからである。回路合成の解の集合は空集合を含む一つ以上の元を含む集合となる。その解の集合を求めることは代数多様体上の有理点を求める問題を解くことに帰着するため簡単ではない。故に、二端子対回路では回路解析のみに限定して、有用な定理や考え方、視点を学ぶのみに止まる。これは有限時間で教えることができ、また学ぶことができる。これを学んだ上で、やっと能動素子や電源を含む回路網の解析や合成ができるようになる。もちろんまったく電気回路理論を学ばなくてもキルヒホッフの法則を知っていれば特定の回路の解析は十分可能であるが、回路を与えられずに与えられた特性を得る回路を合成することは思考錯誤の連続となり有限時間内に解が得られる保証はない。ということでとりあえずしばらくは以下の制約を与えて扱う回路を限定することになる・線形素子(R,L,M,C)のみで構成される・一対の端子の一方から流入する電流は、他方の端子から流出する電流に等しい従って以下の様に一定の回路の外部条件が与えられることになる。従って二端子対回路はE1,I1,E2,E2の中から２つを主要不定元とする組み合わせ $_{4}C_{2}=6$ だけの種類の表現方法があることになる。以降でそれぞれの表現方法について学ぶことにする。

webadm	投稿日時: 2010-5-4 2:58
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	インピーダンス行列（Z行列）ちょうど一端子対回路の駆動点インピーダンスを考えた際に、任意の受動素子と電源から成る回路網内の任意のn個の素子の両端を端子対とするn端子対回路のひとつの端子対を除いてすべてを短絡したものが一端子対回路だったと同様に、二つの端子対を除いてすべてを短絡したものが二端子対回路とみなすことができる。その場合に、２つの端子対の電圧と電流、E1,E2,I1,I2の間には以下の関係が成り立つことになる。 $\left[\begin{array}<br />E_1 \\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left[\begin{array}<br />I_1 \\<br />I_2<br />\end{array}\right]$ ここで係数行列がインピーダンス行列もしくはZ行列とよばれ、行列の各要素はインピーダンスパラメータと呼ぶ。それぞれのインピーダンスパラメータは以下の意味を持つ。端子対1を開放するとI1=0となるため、先の関係式に代入すると $\left[\begin{array}<br />E_1 \\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 \\<br />I_2<br />\end{array}\right]$ $\begin{eqnarray}<br />E_1&=&\left.Z_{12}I_2\right\|_{I_1=0}\\<br />E_2&=&\left.Z_{22}I_2\right\|_{I_1=0}<br />\end{eqnarray}$ 従ってインピーダンスパラメータは $\begin{eqnarray}<br />Z_{12}&=&\left.\frac{E_1}{I_2}\right\|_{I_1=0}\\<br />Z_{22}&=&\left.\frac{E_2}{I_2}\right\|_{I_1=0}<br />\end{eqnarray}$ Z12を開放伝達インピーダンス、Z22を開放駆動点インピーダンスと呼ぶ。同様に端子対2を開放した場合 $\left[\begin{array}<br />E_1 \\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left[\begin{array}<br />I_1 \\<br />0<br />\end{array}\right]$ $\begin{eqnarray}<br />E_1&=&\left.Z_{11}I_1\right\|_{I_2=0}\\<br />E_2&=&\left.Z_{21}I_1\right\|_{I_2=0}<br />\end{eqnarray}$ 従ってインピーダンスパラメータは $\begin{eqnarray}<br />Z_{11}&=&\left.\frac{E_1}{I_1}\right\|_{I_2=0}\\<br />Z_{21}&=&\left.\frac{E_2}{I_1}\right\|_{I_2=0}<br />\end{eqnarray}$ Z11を開放駆動点インピーダンス、Z21を開放伝達インピーダンスと呼ぶ。だいぶ前に、上巻の「回路網解析と基本諸定理」で受動素子(L,C,R,M)のみからなる線形回路網では一般的にインピーダンスマトリックスが対称行列となるため相反定理が成り立つことを学んだ。二端子対回路にも同じことが言える。ここでは上巻の時とは逆に相反定理が成り立つ場合、インピーダンスマトリックスが対称行列であることを確認してみよう。相反定理が成り立つ時には下記の関係式が成り立つことになる。 $\begin{eqnarray}<br />\left.\frac{E_1}{I_2}\right\|_{I_1=0}&=&\left.\frac{E_2}{I_1}\right\|_{I_2=0}<br />\end{eqnarray}$ これは先に定義した開放伝達インピーダンスそのものであるので、置き換えると $\begin{eqnarray}<br />Z_{12}&=&Z_{21}<br />\end{eqnarray}$ ということになる。従って一般的な二端子対回路ではインピーダンスマトリックスは対称行列となるため、独立なインピーダンスパラメータは３つということになる。一方今度は以下の関係が成り立つ二端子対回路は対称回路であると言う。 $\begin{eqnarray}<br />\left.\frac{E_1}{I_1}\right\|_{I_2=0}&=&\left.\frac{E_2}{I_2}\right\|_{I_1=0}<br />\end{eqnarray}$ これは先に定義した開放駆動点インピーダンスそのものであるので、 $\begin{eqnarray}<br />Z_{11}&=&Z_{22}<br />\end{eqnarray}$ ということになる。二端子対回路をインピーダンス行列表現は複数の回路の各端子対を直列接続する場合に都合がよい。 P.S 後半の内容は既に学んでいたことなので、最初なんの疑問もなく書いてしまったのだが、ふと疑問が沸いた。どの参考書にも受動素子のみから成る線形回路網では一般的に相反定理が成り立つとだけ書いてあるが、ひょっとして相反定理が成り立たない例外があるから一般にと断っているのではないだろうかと。そう考えたら眠れなくなってしまった。参考書に書いてあるのを丸飲みしていただけで、実はよくわかっていなかったのである。実際のところ、普通に思いつく範囲の受動素子のみから成る回路は相反定理が成り立つ可逆回路なわけである。マイクロ波送受信機に必ず使用されるサーキュレータが受動素子のみから成る非可逆回路である。サーキュレータは厳密には三端子対回路であるが、ひとつの端子対を終端すればアイソレータという一方向伝送の二端子対回路となる。原理は電磁気学理論の知識を必要とし電気回路理論の範疇を越えてしまうので触れないようにしているようだ。ユニークな受動素子のみから成る非可逆回路を発明すれば特許になるかもしれない。実際検索すると特許がたくさん出てくる。それと、二端子対回路は昔は四端子回路と呼ばれていた時代があったことを古書を色々調べると明らかになる。二端子対回路(Two Terminal Pair Network)なる用語と、これから学ぶ様々な表現は戦後になってフィルタ回路、真空管やトランジスタ電子回路、それにマイクロ波回路の研究が盛んに行われた70年代初頭にGuilleminとその弟子達によって現在の回路網理論の形に体系化されたようである("A century of electrical engineering and computer science at MIT, 1882-1982" MIT Pressより) 一方でそれ以前はどうだったかというと、主に集中定数型のフィルター理論の導入が目的だったようで、リアクタンス回路を前提としたものが古い本では顕著に見られる。戦前のドイツの理論電気学の本ではマイクロ波を扱うために分布定数回路を含めた形に拡張するところで終わっているものがある。この辺がまたしても戦争の傷跡を感じさせる部分でもある。レーダー技術に代表されるマイクロ波技術の研究に力を入れた米国が戦勝国となり、それに遅れたドイツや日本は敗戦国となった。未だに戦争勃発の兆候が見られると軍事力＝技術力みたいな形でようやく技術振興が叫ばれるのは悲しいことである。ドイツ仕込みの四端子回路の本は戦前戦後の日本の古書にもそっくりそのまま出てきている。特徴的なのは、二端子対の電圧の極性が現在のそれと異なっている点とインピーダンス行列、アドミッタンス行列それに四端子定数の３つの表記のみで戦後になって提案されたそれ以外の表記は出てこない点にある。I1が流入方向、I2が流出方向だとすると、外部の電圧源E1,E2は互いに逆極性になる。またドイツの参考書ではインピーダンスパラメータが偏微分方程式になっていることに気づく。なるほど、一方入力変数を0固定として他方で偏微分すればよいわけで。 $\begin{eqnarray}<br />E_1&=&Z_{11}I_1+Z_{12}I_2\\<br />E_2&=&Z_{21}I_1+Z_{22}I_2<br />\end{eqnarray}$ それぞれI1=0とI2=0としたケースでI2とI1で偏微分するとインピーダンスパラメータは $\begin{eqnarray}<br />Z_{11}&=&\left.\frac{\partial{E_1}}{\partial{I_1}}\right\|_{I_2=0}\\<br />Z_{12}&=&\left.\frac{\partial{E_1}}{\partial{I_2}}\right\|_{I_1=0}\\<br />Z_{21}&=&\left.\frac{\partial{E_2}}{\partial{I_1}}\right\|_{I_2=0}\\<br />Z_{22}&=&\left.\frac{\partial{E_2}}{\partial{I_2}}\right\|_{I_1=0}<br />\end{eqnarray}$ ということになる。なんだ簡単じゃないか(´∀` ) 本書の記述はどちらかというと古い伝統に基づいているものの現代知られている表現方法を一通り紹介している、次に学ぶフィルタ理論への準備という意味合いが強い。また高周波やマイクロ波回路で必須のSパラメータ表現は分布定数回路でも出てこない。これらはマイクロ波の専門の講義で扱うことになるからであろう。

webadm	投稿日時: 2010-5-7 10:21
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	アドミッタンス行列（Y行列）先のインピーダンス行列表現の式に、インピーダンス行列の逆行列であるアドミッタンス行列 $\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]^{-1}=\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]$ を両辺に乗じると $\left[\begin{array}<br />I_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1 \\<br />E_2<br />\end{array}\right]$ というように書き直すことができる。端子対1を短絡するとE1=0となるため、先の関係式に代入すると $\left[\begin{array}<br />I_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]\left[\begin{array}<br />0 \\<br />E_2<br />\end{array}\right]$ $\begin{eqnarray}<br />I_1&=&\left.Y_{12}E_2\right\|_{E_1=0}\\<br />I_2&=&\left.Y_{22}E_2\right\|_{E_1=0}<br />\end{eqnarray}$ 従ってアドミッタンスパラメータは $\begin{eqnarray}<br />Y_{12}&=&\left.\frac{I_1}{E_2}\right\|_{E_1=0}\\<br />Y_{22}&=&\left.\frac{I_2}{E_2}\right\|_{E_1=0}<br />\end{eqnarray}$ Y12を短絡伝達アドミッタンス、Y22を短絡駆動点アドミッタンスと呼ぶ。同様に端子対2を短絡した場合 $\left[\begin{array}<br />I_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1 \\<br />0<br />\end{array}\right]$ $\begin{eqnarray}<br />I_1&=&\left.Y_{11}E_1\right\|_{E_2=0}\\<br />I_2&=&\left.Y_{21}E_1\right\|_{E_2=0}<br />\end{eqnarray}$ 従ってアドミッタンスパラメータは $\begin{eqnarray}<br />Y_{11}&=&\left.\frac{I_1}{E_1}\right\|_{E_2=0}\\<br />Y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}<br />\end{eqnarray}$ Y11を短絡駆動点アドミッタンス、Y21を短絡伝達アドミッタンスと呼ぶ。インピーダンス行列と同様に、相反回路では $Y_{12}=Y_{21}$ となり、対称回路では $Y_{11}=Y_{22}$ となる。アドミッタンス行列表現は複数の回路を並列接続する場合に都合がよい。

webadm	投稿日時: 2010-5-7 10:56
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	ハイブリッド行列（H行列）インピーダンス行列がE1,E2それにI1,I2の組み合わせ、その逆がアドミッタンス行列だったのに対して、今度はI1,E2,E1,I2の組み合わせとその逆が以下のハイブリッド行列表現。 $\left[\begin{array}<br />E_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />H_{11} & H_{12}\\<br />H_{21} & H_{22}<br />\end{array}\right]\left[\begin{array}<br />I_1 \\<br />E_2<br />\end{array}\right]$ 端子対1を開放するとI1=0となるため、先の関係式に代入すると $\left[\begin{array}<br />E_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />H_{11} & H_{12}\\<br />H_{21} & H_{22}<br />\end{array}\right]\left[\begin{array}<br />0 \\<br />E_2<br />\end{array}\right]$ $\begin{eqnarray}<br />E_1&=&\left.Y_{12}E_2\right\|_{I_1=0}\\<br />I_2&=&\left.Y_{22}E_2\right\|_{I_1=0}<br />\end{eqnarray}$ 従ってハイブリッドパラメータは $\begin{eqnarray}<br />H_{12}&=&\left.\frac{E_1}{E_2}\right\|_{I_1=0}\\<br />H_{22}&=&\left.\frac{I_2}{E_2}\right\|_{I_1=0}<br />\end{eqnarray}$ H12を開放電圧減衰率、H22を開放駆動点アドミッタンスと呼ぶ。同様に端子対2を短絡した場合E2=0となるので $\left[\begin{array}<br />E_1 \\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />H_{11} & H_{12}\\<br />H_{21} & H_{22}<br />\end{array}\right]\left[\begin{array}<br />I_1 \\<br />0<br />\end{array}\right]$ $\begin{eqnarray}<br />E_1&=&\left.H_{11}E_1\right\|_{E_2=0}\\<br />I_2&=&\left.H_{21}E_1\right\|_{E_2=0}<br />\end{eqnarray}$ 従ってハイブリッドパラメータは $\begin{eqnarray}<br />H_{11}&=&\left.\frac{E_1}{I_1}\right\|_{E_2=0}\\<br />H_{21}&=&\left.\frac{I_2}{I_1}\right\|_{E_2=0}<br />\end{eqnarray}$ H11を短絡駆動点インピーダンス、H21を短絡電流増幅率と呼ぶ。ここで賢明な読者は受動回路ならばI2の電流の向きが逆になるはずなので-I2でなければならず、H21の値には負号が付くはずだと主張するだろう。ところがどっこい、元々ハイブリッド行列はバイポーラ型トランジスタの等価回路のために登場したので、能動回路（等価電流源を内部にもつ）を前提とするため、端子2を短絡しても流れる電流の向きは一定で変わらないという読者の知らない暗黙の了解がある。 Z,Y行列の時と同様に相反回路の場合どうなるかを考えてみよう、端子対1を開放し、端子対2に電圧源E2'を接続した場合に端子対1に現れる電圧をE1'とすると $\begin{eqnarray}<br />{E_1}^\'&=&\left.H_{12}{E_2}^\'\right\|_{I_1=0}\\<br />{I_2}^\'&=&\left.H_{22}{E_2}^\'\right\|_{I_1=0}<br />\end{eqnarray}$ 第一の式をH12で除したものから第二の式をH22で除したものを差し引いてE2'を消去しE1'/I2'を導くと $\begin{eqnarray}<br />\frac{{E_1}^\'}{H_{12}}-\frac{{I_2}^\'}{H_{22}}&=&0\\<br />\frac{{E_1}^\'}{{I_2}^\'}&=&\left.\frac{H_{12}}{H_{22}}\right\|_{I_1=0}<br />\end{eqnarray}$ ということになる。逆に端子対2を開放し、端子対1に電流源I1'を接続した場合、端子対2に現れる電圧がE2'とすると $\begin{eqnarray}<br />{E_1}^\'&=&\left.H_{11}{I_1}^\'+H_{12}{E_2}^\'\right\|_{I_2=0}\\<br />0&=&\left.H_{21}{I_1}^\'+H_{22}{E_2}^\'\right\|_{I_2=0}<br />\end{eqnarray}$ 第二式より $\begin{eqnarray}<br />\frac{{E_2}^\'}{{I_1}^\'}&=&\left.-\frac{H_{21}}{H_{22}}\right\|_{I_2=0}<br />\end{eqnarray}$ ということになる。従ってこれらの結果から相反定理が成り立つ場合には $\begin{eqnarray}<br />\left.\frac{{E_2}^\'}{{I_1}^\'}\right\|_{I_2=0}&=&\left.\frac{{E_1}^\'}{{I_2}^\'}\right\|_{I_1=0}\\<br />\frac{H_{12}}{H_{22}}&=&-\frac{H_{21}}{H_{22}}\\<br />H_{12}&=&-H_{21}<br />\end{eqnarray}$ ということになる。てっきりH12=H21だと信じて疑わなかった人は負け組。さて今度は対称回路の条件を考えてみよう。端子対1を開放し、端子対2に電圧源E2'を接続した場合に端子対1に現れる電圧をE1'とした場合の第二式より $\begin{eqnarray}<br />\left.\frac{{E_2}^\'}{{I_2}^\'}\right\|_{I_1=0}&=&\left.\frac{1}{H_{22}}\right\|_{I_1=0}<br />\end{eqnarray}$ 端子対2を開放し、端子対1に電流源I1'を接続した場合、端子対2に現れる電圧がE2'とした場合の二式からE1'/I1'を導くために第一式をI1'で除したものから第二式にH12/(H22*I1')を乗じたものを差し引くと $\begin{eqnarray}<br />\left.\frac{{E_1}^\'}{{I_1}^\'}\right\|_{I_2=0}&=&\left.\frac{H_{11}H_{22}-H_{12}H_{21}}{H_{22}}\right\|_{I_2=0}<br />\end{eqnarray}$ 従って対称回路では $\begin{eqnarray}<br />\left.\frac{{E_2}^\'}{{I_2}^\'}\right\|_{I_1=0}&=&\left.\frac{{E_1}^\'}{{I_1}^\'}\right\|_{I_2=0}\\<br />\left.\frac{1}{H_{22}}\right\|_{I_1=0}&=&\left.\frac{H_{11}H_{22}-H_{12}H_{21}}{H_{22}}\right\|_{I_2=0}\\<br />H_{11}H_{22}-H_{12}H_{21}&=&\left\|H\right\|=1<br />\end{eqnarray}$ ということになる。このようにハイブリッドパラメータはインピーダンスパラメータやアドミッタンスパラメータと違って、異なるパラメータの単位が混在していることからハイブリッド（混成）行列と呼ばれている。電流増幅作用を持った小信号バイポーラ型トランジスタの性能測定時の小信号パラメータ(小文字でhパラメータと呼ばれる）もHパラメータ行列の応用である。小信号パラメータはHパラメータのH11,H12,H21,H22をhi,hr,hf,hoと呼ぶ。トランジスタはECBの三つの端子があるので、二端子回路を構成する際にどれかひとつが共通（コモン）とするためパラメータの添字の末尾にe,c,bのいずれがつくことになる。エミッタを共通とした場合hieは出力短絡時の入力インピーダンス、hreは入力開放逆電圧増幅率、hfeは出力短絡時の電流増幅率、hoeは入力短絡時の出力アドミッタンスを意味する。hfeは小信号バイポーラ型トランジスタの主たる性能（電流増幅率）指標で、製造時にばらつきがあり、同じ型式のトランジスタでもこの測定値によってランク分けされる。これらの小信号パラメータ測定値を使って実際のトランジスタ増幅回路を設計することも可能であるが、基本的に非線形なので小信号回路に限り線形近似が可能な設計動作点（バイアス電流）でのHパラメータを回路設計者自身で計算や特性表から求めなければならない。それらは電気回路理論ではなく電子回路理論の分担となる。電子回路理論の参考書もしくは電子回路ハンドブックから学ぶしかない。インピーダンス行列とアドミッタンス行列の関係と同様にハイブリッド行列の逆行列がG行列である。 $\left[\begin{array}<br />H_{11} & H_{12}\\<br />H_{21} & H_{22}<br />\end{array}\right]^{-1}=\left[\begin{array}<br />G_{11} & G_{12}\\<br />G_{21} & G_{22}<br />\end{array}\right]$ $\left[\begin{array}<br />I_1 \\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />G_{11} & G_{12}\\<br />G_{21} & G_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1 \\<br />I_2<br />\end{array}\right]$ Gパラメータは電圧入力で電流出力となる真空管や電界効果型トランジスタ(FET)の等価回路解析とかに利用できるがHパラメータと同様に実際に使われることはほとんどないと思われる。相反回路や対称回路の場合の条件はHパラメータと同様に導くことができるので読者の課題としよう(´∀` ) P.S Hパラメータもバイポーラ型トランジスタが登場した当時は扱える周波数も低かったのでパラメータの測定も可能だったが、高周波トランジスタとなるとパラメータの実測定も現実的ではなくなってくる。それに代わって登場したのがSパラメータで、Sパラメータはほとんどすべての回路に関してパラメータが存在するため、今では高周波トランジスタではそちらが設計に不可欠なデータとして提供されている。Sパラメータは不定元が電圧と電流ではなく、信号振幅（信号電力の平方根）に対する無次元係数から成るので二端子対回路パラメータとはその点が大きく異なるが考え方は共通である。いずれにしてもHパラメータはトランジスタのような能動素子や等価電源を含む二端子対回路用途向けなので受動素子のみからなる回路で用いられることはないと思われる。初期のトランジスタ回路の参考書を見ても、しょっぱなからHパラメータを設計で使うのは極めて難しい（困難）と書いてあるものもあるし、Hパラメータは登場した途端に既に歴史上の盲腸と化した感がある。

webadm	投稿日時: 2010-5-8 0:56
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	伝送行列(F行列）戦前から線形受動素子のみから成る伝送回路を縦続接続した系を解析するために考案されたのが伝送行列(transmission matrix)もしくは継続行列(chain matrix)と呼ばれるF行列(基本行列：Fundamentarl matrix)。これまでの表現方法と端子対2の電流の向きが逆である。明らかに端子対1が入力で端子対2が出力ポートに相当することがわかる。端子対の電圧と電流のペアを不定元とする以下の回路方程式で表される。 $\begin{eqnarray}<br />E_1&=&A E_2+B I_2\\<br />I_1&=&C E_2+D I_2<br />\end{eqnarray}$ 行列表記では $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B \\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ F行列の要素A,B,C,Dが四端子定数(four terminal constant)と古くから呼ばれているもの。入力端子対2を開放するとI2=0となるので４端子対定数は $\begin{eqnarray}<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}<br />\end{eqnarray}$ 出力端子対2を短絡するとE2=0となるので残る４端子対定数は $\begin{eqnarray}<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}<br />\end{eqnarray}$ Aを開放電圧減衰率、Bを短絡伝達インピーダンス、Cを開放伝達アドミッタンス、Dを短絡電流減衰率と呼ぶ。端子対2を短絡して端子対1に電圧源E1'を接続した場合に、端子対2に流れる電流がI2'だったとし、逆に端子対1を短絡し端子対2に電圧源E2'を接続した場合に、端子対1に流れる電流がI1'だとすると、相反回路であれば以下の関係が成り立つ。 $\frac{{E_1}^\'}{{I_2}^\'}=\frac{{E_2}^\'}{{I_1}^\'}$ 従ってE1=E1',I2=I2',E2=0を先の伝送行列表現の式に代入すると $\begin{eqnarray}<br />{E_1}^\'&=&B {I_2}^\'\\<br />{I_1}^\'&=&D {I_2}^\'<br />\end{eqnarray}$ 従ってE1'/I2'は $\begin{eqnarray}<br />\left.\frac{{E_1}^\'}{{I_2}^\'}\right\|_{{E_2}^\'=0}&=&B<br />\end{eqnarray}$ 一方E2=E2',I2=-I2',I1=-I1',E1=0を先の伝送行列表現の式に代入すると $\begin{eqnarray}<br />0&=&A {E_2}^\'-B {I_2}^\'\\<br />-{I_1}^\'&=&C {E_2}^\'-D {I_2}^\'<br />\end{eqnarray}$ 第一の式の両辺をBで除したものから、第二の式の両辺をDで除したものを差し引いてI2'を消去するとE2'とI1'の関係式が導かれる $\begin{eqnarray}<br />\frac{1}{D}{I_1}^\'&=&\frac{A}{B}{E_2}^\'-\frac{C}{D}{E_2}^\'\\<br />&=&\left(\frac{A D-B C}{B D}\right){E_2}^\'\\<br />\left.\frac{{E_2}^\'}{{I_1}^\'}\right\|_{{E_1}^\'=0}&=&\frac{B}{A D - B C}\\<br />\end{eqnarray}$ 従って相反定理が成り立つためには以下が成り立つ必要がある。 $\begin{eqnarray}<br />\left.\frac{{E_1}^\'}{{I_2}^\'}\right\|_{{E_2}^\'=0}&=&\left.\frac{{E_2}^\'}{{I_1}^\'}\right\|_{{E_1}^\'=0}\\<br />B&=&\frac{B}{A D - B C}\\<br />A D- B C&=&1<br />\end{eqnaray}$ 従ってAD-BCはF行列の行列式そのものなので $\left\|F\right\|=\left\|\begin{array}A & B\\ C & D\end{array}\right\|=A D - BC = 1$ ということになる。また対称回路の場合には先のE1=E1',I2=I2',E2=0の回路方程式よりI2'を消去してE1'/I1'を導くと $\begin{eqnarray}<br />\left.\frac{{E_1}^\'}{{I_1}^\'}\right\|_{E_2=0}&=&\left.\frac{B}{D}\right\|_{E_2=0}<br />\end{eqnarray}$ 一方E2=E2',I2=-I2',I1=-I1',E1=0の条件の回路方程式からE2'/I2'を導くと $\begin{eqnarray}<br />\left.\frac{{E_2}^\'}{{I_2}^\'}\right\|_{E_1=0}&=&\left.\frac{B}{A}\right\|_{E_1=0}<br />\end{eqnarray}$ 従って対称回路では $\begin{eqnarray}<br />\left.\frac{{E_1}^\'}{{I_1}^\'}\right\|_{E_2=0}&=&\left.\frac{{E_2}^\'}{{I_2}^\'}\right\|_{E_1=0}\\<br />\left.\frac{B}{D}\right\|_{E_2=0}&=&\left.\frac{B}{A}\right\|_{E_1=0}\\<br />A&=&D<br />\end{eqnarray}$ ということになる。またF行列と逆の端子対を不定元とした表現をFi行列と呼ぶ。ただしZ行列とY行列や、H行列とG行列の時と違って、端子対の電流の向きがF行列の逆とするためFi行列はF行列の逆行列ではない。上記の回路のFiパラメータによる回路方程式は $\begin{eqnarray}<br />E_2&=&A_i E_1+B_i I_1\\<br />I_2&=&C_i E_1+D_i I_1<br />\end{eqnarray}$ Fi行列表記だと $\begin{eqnarray}<br />\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />A_i & B_i \\<br />C_i & D_i<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]<br />\end{eqnarray}$ Fi行列がF行列の逆行列ではないという意味は、F行列の式でI1,I2を逆向き（負号付き）にしたものにF行列の逆行列を乗じて、I1,I2の負号を逆行列の要素側に転じたものであるためである。 Fパラメータの回路方程式をFiパラメータの時とI1,I2を逆向きにすると $\begin{eqnarray}<br />E_1&=&A E_2-B I_2\\<br />-I_1&=&C E_2-D I_2<br />\end{eqnarray}$ 行列表記では $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />-I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B \\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />-I_2<br />\end{array}\right]<br />\end{eqnarray}$ 両辺にF行列の逆行列 $\begin{eqnarray}<br />\left[F\right]^{-1}&=&\frac{1}{\left\|F\right\|}\left[\begin{array}<br />D & -B \\<br />-C & A<br />\end{array}\right]<br />\end{eqnarray}$ を乗じてI1,I2の負号を行列要素側に転じると $\begin{eqnarray}<br />\frac{1}{\left\|F\right\|}\left[\begin{array}<br />D & -B \\<br />-C & A<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />-I_1<br />\end{array}\right]&=&\left[\begin{array}<br />E_2\\<br />-I_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]&=&\frac{1}{\left\|F\right\|}\left[\begin{array}<br />D & B \\<br />C & A<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]<br />\end{eqnarray}$ 従ってF行列とFi行列の関係は $\begin{eqnarray}<br />\left[F_i\right]&=&\left[\begin{array}<br />A_i & B_i \\<br />C_i & D_i<br />\end{array}\right]=\frac{1}{\left\|F\right\|}\left[\begin{array}<br />D & B \\<br />C & A<br />\end{array}\right]\ne\left[F\right]^{-1}=\frac{1}{\left\|F\right\|}\left[\begin{array}<br />D & -B \\<br />-C & A<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。 Fi行列も同様に相反回路では $\left\|F_i\right\|=\left\|\begin{array}A_i & B_i\\ C_i & D_i\end{array}\right\|=A_i D_i - B_i C_i = 1$ が成り立つ。また対称回路では $\begin{eqnarray}<br />A_i&=&D_i<br />\end{eqnarray}$ ということになる。証明は読者の課題としよう(´∀` ) Fi行列が用いられる場面は非常に限定的なので紹介している参考書もすくない。本書でも紹介すらされていない。これで６種類の組み合わせが全部出そろったことになる。Z,Y,H,G,Fパラメータ間の相互変換表を示しているが、ここまで誤記誤植は見あたらなかったのが、ここに来てチョンボしてHパラメータとFパラメータの相反回路と対称回路の条件が入れ替わってしまっている。こうなると変換表の他の部分にも誤記があるのではないかと疑われるのは致し方がない。ソフトウェアも一個バグを出しただけで開発者は依頼主から「他にもまだバグが潜んでいるのでは？」と一生涯疑われるのだからたまったものではない。ソフトウェアにバグはつきものドキュメントに誤記誤植はあって当たり前と前もって了解してもらえれば免責される。現実的に誤記誤植やバグを完全になくす責務など最初から負えるはずもない。そうした免責が許されるからソフトウェア開発はどんどん工賃の安い国で行われるようになる。当然バグがあっても依頼主は開発者に責任を問えるはずもない。自動車の制御ソフトだってそういう時代なのだから、日本人的な考えで開発者に無限責任ありと簡単に責任転嫁できない。依頼主にとって都合の悪い致命的なバグが無いか検査するのは今や依頼主側の責任となるのだから。電車の車両事故も安全運転の責務を持つ運転手が無限責任を負い経営者が免責されるというのもおかしい話しである。そうだとすれば運転手の方が経営者よりも報酬が多くなければならない。ただ昨今のトヨタ叩きによって自動車メーカー各社が一斉にMicrosoftのように製品に重大な欠陥や特定ユーザーの用途に不適合であることが購入後に発見された場合に、製品購入代金以上の賠償責任を負わないという免責事項を購入時の契約書に忍び込ませたとしたら世界経済への影響は計りしれない。余談が過ぎたようだ。本書には他にも代表的な二端子対回路網のパラメータが表になって示されている。内容を鵜呑みにする前に誤りが無いか確認するのは読者の責務である、caveat emptor! P.S Fパラメータの条件を間違えてI1=0としていたが、I2=0の誤りだった...orz (2010/05/26)

webadm	投稿日時: 2010-5-9 11:00
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	二端子対回路の接続任意の二端子対回路の組み合わせることによって、より大きな二端子対回路を構成することが可能である。 (1)縦続接続アナログ電話網は２つの接続中の電話器から見ると一種の二端子対回路に見える。更に電話網は伝送路である回線で増幅器や等価器、フィルター、ハイブリッド回路が縦続接続されたものである。こうした縦続接続を取り扱うためには伝送行列が都合が良い。例えば、以下の様に２つの異なる二端子対回路を縦続接続して一個の大きな二端子対回路にする場合、以下の関係が成り立つとする $\begin{eqnarray}\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A_1 & B_1 \\<br />C_1 & D_1<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ $\begin{eqnarray}\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />A_2 & B_2 \\<br />C_2 & D_2<br />\end{array}\right]\left[\begin{array}<br />E_3\\<br />I_3<br />\end{array}\right]<br />\end{eqnarray}$ 第一の式に第二の式を代入すると $\begin{eqnarray}\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A_1 & B_1 \\<br />C_1 & D_1<br />\end{array}\right]\left[\begin{array}<br />A_2 & B_2 \\<br />C_2 & D_2<br />\end{array}\right]\left[\begin{array}<br />E_3\\<br />I_3<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />A_1 A_2+C_1 C_2 & A_1 B_2+B_1 D_2 \\<br />C_1 A_2+D_1 C_2 & C_1 B_2+D_1 D_2<br />\end{array}\right]\left[\begin{array}<br />E_3\\<br />I_3<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />A & B \\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_3\\<br />I_3<br />\end{array}\right]<br />\end{eqnarray}$ 従って全体の二端子対回路の伝送行列は $\begin{eqnarray}\left[\begin{array}<br />A & B \\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />A_1 & B_1 \\<br />C_1 & D_1<br />\end{array}\right]\left[\begin{array}<br />A_2 & B_2 \\<br />C_2 & D_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />A_1 A_2+C_1 C_2 & A_1 B_2+B_1 D_2 \\<br />C_1 A_2+D_1 C_2 & C_1 B_2+D_1 D_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。（２）直列接続複数の二端子対回路の各端子対が直列に接続されて全体でひとつの二端子対回路を構成することが出来る。その場合には、インピーダンス行列が都合が良い。以下の関係が成り立つとする $\begin{eqnarray}\left[\begin{array}<br />{E_1}^\'\\<br />{E_2}^\'<br />\end{array}\right]&=&\left[\begin{array}<br />{Z_{11}}^\' & {Z_{12}}^\' \\<br />{Z_{21}}^\' & {Z_{22}}^\'<br />\end{array}\right]\left[\begin{array}<br />{I_1}^\'\\<br />{I_2}^\'<br />\end{array}\right]<br />\end{eqnarray}$ $\begin{eqnarray}\left[\begin{array}<br />{E_1}^{\'\'}\\<br />{E_2}^{\'\'}<br />\end{array}\right]&=&\left[\begin{array}<br />{Z_{11}}^{\'\'} & {Z_{12}}^{\'\'} \\<br />{Z_{21}}^{\'\'} & {Z_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{I_1}^{\'\'}\\<br />{I_2}^{\'\'}<br />\end{array}\right]<br />\end{eqnarray}$ ここで $\begin{eqnarray}<br />E_1&=&{E_1}^{\'}+{E_1}^{\'\'}\\<br />E_2&=&{E_2}^{\'}+{E_2}^{\'\'}\\<br />I_1&=&{I_1}^{\'}={I_1}^{\'\'}\\<br />I_2&=&{I_2}^{\'}={I_2}^{\'\'}<br />\end{eqnarray}$ であるので $\begin{eqnarray}\left[\begin{array}<br />{E_1}\\<br />{E_2}<br />\end{array}\right]&=&\left[\begin{array}<br />{E_1}^{\'}\\<br />{E_2}^{\'}<br />\end{array}\right]+\left[\begin{array}<br />{E_1}^{\'\'}\\<br />{E_2}^{\'\'}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Z_{11}}^{\'} & {Z_{12}}^{\'} \\<br />{Z_{21}}^{\'} & {Z_{22}}^{\'}<br />\end{array}\right]\left[\begin{array}<br />{I_1}\\<br />{I_2}<br />\end{array}\right]+\left[\begin{array}<br />{Z_{11}}^{\'\'} & {Z_{12}}^{\'\'} \\<br />{Z_{21}}^{\'\'} & {Z_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{I_1}\\<br />{I_2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Z_{11}}^{\'}+{Z_{11}}^{\'\'} & {Z_{12}}^{\'}+{Z_{12}}^{\'\'} \\<br />{Z_{21}}^{\'}+{Z_{21}}^{\'\'} & {Z_{22}}^{\'}+{Z_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{I_1}\\<br />{I_2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Z_{11}} & {Z_{12}}\\<br />{Z_{21}} & {Z_{22}}<br />\end{array}\right]\left[\begin{array}<br />{I_1}\\<br />{I_2}<br />\end{array}\right]<br />\end{eqnarray}$ 従って全体の二端子対回路のインピーダンス行列は $\begin{eqnarray}\left[\begin{array}<br />{Z_{11}} & {Z_{12}}\\<br />{Z_{21}} & {Z_{22}}<br />\end{array}\right]&=&\left[\begin{array}<br />{Z_{11}}^{\'}+{Z_{11}}^{\'\'} & {Z_{12}}^{\'}+{Z_{12}}^{\'\'} \\<br />{Z_{21}}^{\'}+{Z_{21}}^{\'\'} & {Z_{22}}^{\'}+{Z_{22}}^{\'\'}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。（３）並列接続同様に複数の二端子対回路の端子対を並列接続することによって多きな二端子対回路を構成することができる。この場合にはアドミッタンス行列を使うと都合がよい。以下の関係が成り立つとする $\begin{eqnarray}\left[\begin{array}<br />{I_1}^\'\\<br />{I_2}^\'<br />\end{array}\right]&=&\left[\begin{array}<br />{Y_{11}}^\' & {Y_{12}}^\' \\<br />{Y_{21}}^\' & {Y_{22}}^\'<br />\end{array}\right]\left[\begin{array}<br />{E_1}^\'\\<br />{E_2}^\'<br />\end{array}\right]<br />\end{eqnarray}$ $\begin{eqnarray}\left[\begin{array}<br />{I_1}^{\'\'}\\<br />{I_2}^{\'\'}<br />\end{array}\right]&=&\left[\begin{array}<br />{Y_{11}}^{\'\'} & {Y_{12}}^{\'\'} \\<br />{Y_{21}}^{\'\'} & {Y_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{E_1}^{\'\'}\\<br />{E_2}^{\'\'}<br />\end{array}\right]<br />\end{eqnarray}$ ここで $\begin{eqnarray}<br />I_1&=&{I_1}^{\'}+{I_1}^{\'\'}\\<br />I_2&=&{I_2}^{\'}+{I_2}^{\'\'}\\<br />E_1&=&{E_1}^{\'}={E_1}^{\'\'}\\<br />E_2&=&{E_2}^{\'}={E_2}^{\'\'}<br />\end{eqnarray}$ であるので $\begin{eqnarray}\left[\begin{array}<br />{I_1}\\<br />{I_2}<br />\end{array}\right]&=&\left[\begin{array}<br />{I_1}^{\'}\\<br />{I_2}^{\'}<br />\end{array}\right]+\left[\begin{array}<br />{I_1}^{\'\'}\\<br />{I_2}^{\'\'}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Y_{11}}^{\'} & {Y_{12}}^{\'} \\<br />{Y_{21}}^{\'} & {Y_{22}}^{\'}<br />\end{array}\right]\left[\begin{array}<br />{E_1}\\<br />{E_2}<br />\end{array}\right]+\left[\begin{array}<br />{Y_{11}}^{\'\'} & {Y_{12}}^{\'\'} \\<br />{Y_{21}}^{\'\'} & {Y_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{E_1}\\<br />{E_2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Y_{11}}^{\'}+{Y_{11}}^{\'\'} & {Y_{12}}^{\'}+{Y_{12}}^{\'\'} \\<br />{Y_{21}}^{\'}+{Y_{21}}^{\'\'} & {Y_{22}}^{\'}+{Y_{22}}^{\'\'}<br />\end{array}\right]\left[\begin{array}<br />{E_1}\\<br />{E_2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{Y_{11}} & {Y_{12}}\\<br />{Y_{21}} & {Y_{22}}<br />\end{array}\right]\left[\begin{array}<br />{E_1}\\<br />{E_2}<br />\end{array}\right]<br />\end{eqnarray}$ 従って全体の二端子対回路のアドミッタンス行列は $\begin{eqnarray}\left[\begin{array}<br />{Y_{11}} & {Y_{12}}\\<br />{Y_{21}} & {Y_{22}}<br />\end{array}\right]&=&\left[\begin{array}<br />{Y_{11}}^{\'}+{Y_{11}}^{\'\'} & {Y_{12}}^{\'}+{Y_{12}}^{\'\'} \\<br />{Y_{21}}^{\'}+{Y_{21}}^{\'\'} & {Y_{22}}^{\'}+{Y_{22}}^{\'\'}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。なんだ簡単じゃないか(´∀` ) アドミッタンス行列表現による並列接続は重ね合わせ効くので最も有用である。フィルタ、高周波回路やマイクロ波の導波管理論でも頻繁に登場する。ところが、著者は特に書いていないがすべての二端子対回路で直列接続や並列接続が成り立つわけではない。共通帰還線（共通GND)を持たない二端子対回路と、共通帰還線を持つ二端子回路を並列接続や直列接続すると端子対条件を満たさなくなるためである。接続することによって端子対条件が満たさなくなってしまう簡単な例でそれを確かめることができる。個々の二端子対回路のアドミッタンス行列表現は $\begin{eqnarray}\left[\begin{array}<br />{I_1}^\'\\<br />{I_2}^\'<br />\end{array}\right]&=&\left[\begin{array}<br />Y_1 & -Y_1 \\<br />-Y_1 & Y_1<br />\end{array}\right]\left[\begin{array}<br />{E_1}^\'\\<br />{E_2}^\'<br />\end{array}\right]<br />\end{eqnarray}$ $\begin{eqnarray}\left[\begin{array}<br />{I_1}^{\'\'}\\<br />{I_2}^{\'\'}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_2+\frac{Y_3 Y_4}{Y_3+Y_4} & -\frac{Y_3 Y_4}{Y_3+Y_4}\\<br />-\frac{Y_3 Y_4}{Y_3+Y_4} & Y_5+\frac{Y_3 Y_4}{Y_3+Y_4}<br />\end{array}\right]\left[\begin{array}<br />{E_1}^{\'\'}\\<br />{E_2}^{\'\'}<br />\end{array}\right]<br />\end{eqnarray}$ 最初の小回路は端子対の間で共通帰還線をもつが、二番目の小回路は共通帰還線をもたない。この２つの小回路を並列接続すると最初の小回路の共通帰還線で二番目の小回路のY4が短絡されてしまって回路上消滅してしまい、各小回路のアドミッタンス行列の和 $\begin{eqnarray}\left[\begin{array}<br />Y_1+Y_2+\frac{Y_3 Y_4}{Y_3+Y_4} & -Y_1-\frac{Y_3 Y_4}{Y_3+Y_4}\\<br />-Y_1-\frac{Y_3 Y_4}{Y_3+Y_4} & Y_1+Y_5+\frac{Y_3 Y_4}{Y_3+Y_4}<br />\end{array}\right]<br />\end{eqnarray}$ と全体の回路のアドミッタンス行列 $\begin{eqnarray}\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_1+Y_2+Y_3 & -Y_1-Y_3\\<br />-Y_1-Y_3 & Y_1+Y_3+Y_5<br />\end{array}\right]<br />\end{eqnarray}$ は異なるものとなってしまう。共通帰還線を持たない回路と持つ回路を並列接続もしくは直列接続する際には、以下の様にいずれかの端子対に1:1の理想変成器（絶縁トランス）を挿入すれば上記の問題は回避できるが、トランスを入れるのはやっかいである。このトランスは等価回路で置き換えるわけにはいかない。幸いにして、実際の回路は共通帰還線を持っており、共通帰還線同士を接続する分には問題ない。ただし端子対を逆接続して共通帰還線でない端子を他の回路の共通帰還線端子に接続してしまうと問題が発生する。従って回路の共通帰還線（共通GND)が端子対のどちらの端子に出てきているのか他の回路や機器と接続する前に確認することは実務上不可欠である。昔老舗の電子顕微鏡メーカーに別の製品（磁気テープ装置）の納品に付き合った時に、受け入れ検査担当の購買部のおじさんが、コンピュータにつないで動作確認する際に、アナログテスターでグランドが共通になっているか念入りに指先確認してから電源を入れていたのが印象に残っている。さすが昔からの技術者は基本に忠実である。それだから会社が大きくなれたのだろう。 P.S 行列の掛け算について良くわかってなかったことに気づいたのは内緒だ。

webadm	投稿日時: 2010-5-10 12:46
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	影像パラメータここでは影像インピーダンスと伝達定数から成る影像パラメータを学ぶ。影像パラメータは戦前に米国（Otto J. Zobel、George Campbell、Sidney Darlington、M. Reedら）で体系化された古典的な影像フィルタ理論の一部である。戦後になってトランジスタやオペアンプが登場して以来、近代的なフィルタ理論が登場し古典的な理論は隅へ追いやられた感がある。元来は戦前に発明され需用が急拡大していった電話網の伝送路内に挿入する低損失な受動素子からのみなる等価器やフィルタの研究開発に端を発する理論である。既にここまでで、二端子回路の縦続接続について学んだが、それで電話網に導入する受動素子フィルタを設計する上でひとつ問題が持ち上がる。最終端子対に負荷を接続した場合に縦続接続されている各小回路の出力端子対の出力インピーダンスが、後続する小回路の入力端子対の駆動点インピーダンスと等しくないと最大電力が供給されないという問題である。最悪入力された信号がほとんど出力に出てこないことになってしまう。これではまったく役にたたない。このことは本書を含め電気回路のほとんどの参考書に書かれていないことで、あくまで個人的な推測である。一体何故影像インピーダンスを持ち出さなければならないのかその理由が知りたかったのであるが、考案されたのが戦前なので、もうすでに研究者も亡くなって久しいため知るよしもない。想像するしかないのである。上記の仮説に基づいて、戦前に立ち戻って上記の問題を解決しようとすると、影像インピーダンスというアイデアの真意が理解できるわけである。著者の記述は最初からまとめに走っているので鵜呑みにしようにも喉を通らない。そこでもっとゆっくり考えて見ることにする。（１）影像インピーダンス(image impedances) 著者もそうだが、影像インピーダンスの英語表記を単数のimage impedanceと書いている。日本語だと複数と単数の区別ができないのだがオリジナルは複数形である。つまり一般的に影像インピーダンスは２つあることを意味する。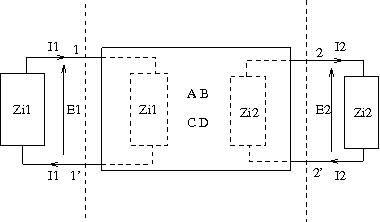一般的（相反で非対称）な二端子対回路の２つの端子対をそれぞれZi1とZi2のインピーダンスで終端した場合に、端子対1-1'から見た駆動点インピーダンスが端子対1-1'に接続されたZi1と等しく、端子対2-2'から見た駆動点インピーダンスが端子対2-2'に接続されたZi2に等しくなるようなZi1,Zi2を影像インピーダンス(image impedances)と呼ぶ。(2010/8/21訂正）つまり図にあるように端子対を境界線とすると境界の左右でインピーダンスが同一であるかのように見えるということを意味する。一般的に二端子対回路が非対称回路の場合、Zi1≠Zi2であるが対称回回路の場合はZi1＝Zi2となる。著者は矢継ぎ早に伝達定数の定義に入っているが、ちょっとその前に影像インピーダンスについてもっとよく知る必要がある。上図でZi1,Zi2がFパラメータでどのように表されるのか考えてみよう。 Zi1は $\begin{eqnarray}<br />Z_{i1}&=&\frac{E_1}{I_1}\\<br />&=&\frac{A E_2+B I_2}{C E_2+D I_2}\\<br />&=&\frac{A Z_{i2}I_2+B I_2}{C Z_{i2}I_2+D I_2}\\<br />&=&\frac{A Z_{i2}+B}{C Z_{i2}+D}<br />\end{eqnarray}$ Zi2はFiパラメータを使用して求めてもよいがAとDが逆になるだけなので書き換えると $\begin{eqnarray}<br />Z_{i2}&=&\frac{E_2}{I_2}\\<br />&=&\frac{D E_1+B I_1}{C E_1+A I_1}\\<br />&=&\frac{D Z_{i1}I_1+B I_1}{C Z_{i1}I_1+A I_1}\\<br />&=&\frac{D Z_{i1}+B}{C Z_{i1}+A}<br />\end{eqnarray}$ ということになる。ここでZi1、Zi2それぞれ∞とすると終端開放時のインピーダンス(Zo1,Zo2)が、Zi1,Zi2をそれぞれ0とすると終端短絡時のインピーダンス(Zs1,Zs2)が導かれる。これは後で重要になる。 $\begin{eqnarray}<br />Z_{o1}&=&\lim_{Z_{i2}\to\infty}\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\lim_{Z_{i2}\to\infty}\frac{A+\frac{B}{Z_{i2}}}{C+\frac{D}{Z_{i2}}}\\<br />&=&\frac{A}{C}<br />Z_{o2}&=&\lim_{Z_{i1}\to\infty}\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\lim_{Z_{i1}\to\infty}\frac{D+\frac{B}{Z_{i1}}}{C+\frac{A}{Z_{i1}}}\\<br />&=&\frac{D}{C}\\<br />Z_{s1}&=&\lim_{Z_{i2}\to0}\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\frac{B}{D}<br />Z_{s2}&=&\lim_{Z_{i1}\to0}\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\frac{B}{A}<br />\end{eqnarray}$ ここで先のZi1,Zi2の式からそれぞれZi2,Zi1を消去すると $\begin{eqnarray}<br />Z_{i1}&=&\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\frac{A \frac{D Z_{i1}+B}{C Z_{i1}+A}+B}{C \frac{D Z_{i1}+B}{C Z_{i1}+A}+D}\\<br />&=&\frac{\frac{A D Z_{i1}+A B+B\left(C Z_{i1}+A\right)}{\cancel{C Z_{i1}+A}}}{\frac{C D Z_{i1}+C B+D\left(C Z_{i1}+D\right)}{\cancel{C Z_{i1}+A}}}\\<br />&=&\frac{\left(A D+B C\right)Z_{i1}+2 A B}{2 C D Z_{i1}+A D+B C}\\<br />&=&\frac{\frac{A D+B C}{2 C D}Z_{i1}+\frac{A B}{C D}}{Z_{i1}+\frac{A D+B C}{2 C D}}\\<br />Z_{i1}\left(Z_{i1}+\frac{A D+B C}{2 C D}\right)&=&\frac{A D+B C}{2 C D}Z_{i1}+\frac{A B}{C D}\\<br />{Z_{i1}}^2&=&\frac{A B}{C D}=Z_{o1}Z_{s1}\\<br />Z_{i1}&=&\pm\sqrt{Z_{o1}Z_{s1}}\\<br />Z_{i2}&=&\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\frac{D \frac{A Z_{i2}+B}{C Z_{i2}+D}+B}{C \frac{A Z_{i2}+B}{C Z_{i2}+D}+A}\\<br />&=&\frac{\frac{A D Z_{i2}+B D+B\left(C Z_{i2}+D\right)}{\cancel{C Z_{i2}+D}}}{\frac{A C Z_{i2}+B C+A\left(C Z_{i2}+D\right)}{\cancel{C Z_{i2}+D}}}\\<br />&=&\frac{\left(A D+B C\right)Z_{i2}+2 B D}{2 A C Z_{i2}+A D+B C}\\<br />&=&\frac{\frac{A D+B C}{2 A C}Z_{i2}+\frac{B D}{A C}}{Z_{i2}+\frac{A D+B C}{2 A C}}\\<br />Z_{i2}\left(Z_{i2}+\frac{A D+B C}{2 A C}\right)&=&\frac{A D+B C}{2 A C}Z_{i2}+\frac{B D}{A C}\\<br />{Z_{i2}}^2&=&\frac{B D}{A C}=Z_{o2}Z_{s2}\\<br />Z_{i2}&=&\pm\sqrt{Z_{o2}Z_{s2}}<br />\end{eqnarray}$ ということになる。厳密にはZi1,Zi2に±の２つの極性があることになるが、受動回路ではインピーダンスの実数部が負になるような負性抵抗や負のインピーダンスは存在しない。能動回路や、ポテンシャル場が支配的な半導体や超電導素子のような微小な量子結晶構造を伴う分布定数回路ではどちらの極性をもとり得る。Maxwellの方程式からスカラー項を取り除いてベクトル項から成る現在知られる簡易な式に書き換えたのはHeavisideだが、自身では負の抵抗の存在の可能性を考えていたのは皮肉だ。後にHeavisideが取り除いたスカラー項は近代になってポテンシャル場の存在が確認されるに至って復活することになった。得に結晶構造内での電磁気現象を扱う必要のある半導体分野では正負両方あると考えると都合がよい。対称回路では２つの影像インピーダンスは互いに等しく $Z_{i1}=Z_{i2}=Z_i$ と単一の影像インピーダンス(Zi)で表され、また対称回路ではA=Dとなるので $\begin{eqnarray}<br />{Z_i}^2&=&{Z_{i1}}^2=\frac{\cancel{A} B}{C \cancel{D}}={Z_{i2}}^2=\frac{B \cancel{D}}{\cancel{A} C}=\frac{B}{C}=Z_{o1}Z_{s2}=Z_{s1}Z_{o2}\\<br />Z_i&=&Z_{i1}=Z_{i2}=\pm\sqrt{Z_{o1}Z_{s2}}=\pm\sqrt{Z_{s1}Z_{o2}}<br />\end{eqnarray}$ ということになる。ここでもZiには正負両極性考えられるが、受動回路では正極性のみに限定される。（２）影像伝達定数(image transfer constant) さて残るは伝達定数。著者はいきなり結論だけ示しているがこれだけだと何が何やら。そもそも損失の無いリアクタンス回路からなる二端子対回路をインピーダンス整合させて縦続接続すれば供給される電力は最終端の負荷で消費される電力と等しくなるが（理想的なリアクタンス回路は電力を消費しない）、現実の回路はなんらかの損失を伴う（RやGが含まれる）ため回路内で電力が消費されるので出力側に供給される電力はその分目減りする。そうした損失を伴う二端子対回路（フィルターやイコライザー）を複数縦続接続して電話網の伝送路に挿入した場合にどれだけ信号が減衰するかを予め計算する必要がある。途中に減衰分を補う増幅回路を追加する必要があるからだ。縦続接続された各二端子回路の入力と出力の電力比が計算できたとすると、全体の入力と出力の電力比は、各電力比の乗除算になる。これだと計算がやっかいなので、戦前に既にベル研究所の研究者達はその比率を対数に変換することで、乗除算ではなく加減算で全体の電力伝達比を簡単に計算できるように考えた。戦後になって常用対数に基づくdB(デジベル）が標準となったが、それ以前は理論的な自然対数に基づくNp(ネーパ）が主だった。現代的なフィルタ理論とコンピュータが登場する以前は、机上での解析や手計算が容易な最小規模の二端子対回路としてフィルタ回路を設計し、それを複数接続することによって試行錯誤的に目的に見合うフィルタを設計していたという時代的な背景がある。その頃の考え方から説明する参考書は現代でもわずかながらある。しかし新しい入門書では影像パラメータそのものが割愛されてしまっているケースがほとんどである。特に現代的なフィルタ理論を学ぶ上では、既に二端子回路で学んだような複素有理関数で表される伝達関数として一度正規化されたフィルタを設計すれば、コンピュータプログラムを使って同一回路でスケーリングファクタを変えるだけで任意の周波数とインピーダンスのフィルタに必要な定数を割り出すことができる。これは既に二端子回路で学んだ通りである。それでも考え方としては現在でも様々な局面で登場するものなので知っておいても損はないという感じである。手元にある参考書で最も古いと思われるものでは、1932年に初版が出版された、ドイツのK. K醇аfm醇・lerによる,「 Einf醇・rung in die theoretische Elektrotechnik」英文に題名を訳すと [Introduction to the theory of electrical engineering]の戦後復刻版(1959年版）に明快な解説を見いだすことができた。K. K醇аfm醇・lerは戦前(1931年)に同じ頃Nyquistが予想し米国で発表していた信号の再現限界周波数（Nyquist周波数と呼ばれる）を独立に発見し論文を発表していたことが戦後になって知られるにいたったことで有名である。ドイツでは現在もこの本の改訂新版が理論電気学の教科書になっているらしい。その本の内容から学ぶべきことは現代的な表現で紹介することにしよう。伝達定数(transfer constant)で検索すると異なる分野で同じ用語が使用されている。影像パラメータのそれは古くは影像伝搬定数もしくは影像伝達定数(image transfer constant)が呼ぶのが正しいようだ。既に科学辞書にしかまともな定義を見出すことはできない始末だ。 Sci-Tech Dictionary: image transfer constant (′im·ij ′tranz·fər ′k醇Bn·stənt) (electronics) One-half the natural logarithm of the complex ratio of the steady-state apparent power entering and leaving a network terminated in its image impedance. （電気）影像インピーダンスで終端された回路網において定常状態で流入及び流出する見掛け上の電力の複素比率を自然対数で表した値の1/2。これの意味から考えるのがよさそうである。最初の影像インピーダンスの図に端子対1-1'側に電源を挿入したものを考える。ここで端子対1-1'側から回路に供給される見かけ上の電力P1は $\begin{eqnarray}<br />P_1&=&E_1 I_1\\<br />&=&E_1\frac{E_1}{Z_{i1}}\\<br />&=&\frac{{E_1}^2}{Z_{i1}}\\<br />&=&\frac{{Z_{i1}}^2{I_1}^2}{Z_{i1}}\\<br />&=&Z_{i1}{I_1}^2<br />\end{eqnarray}$ と表される。一方端子対2-2'の負荷側に供給される見かけ上の電力P2は $\begin{eqnarray}<br />P_2&=&E_2 I_2\\<br />&=&E_2\frac{E_2}{Z_{i2}}\\<br />&=&\frac{{E_2}^2}{Z_{i2}}\\<br />&=&\frac{{Z_{i2}}^2{I_2}^2}{Z_{i2}}\\<br />&=&Z_{i2}{I_2}^2<br />\end{eqnarray}$ と表される。影像伝達定数は先の定義によりP1とP2の比の自然対数を1/2したものであるので $\begin{eqnarray}<br />\theta&=&\frac{1}{2}\ln\frac{P_1}{P_2}\\<br />2\theta&=&\ln\frac{P_1}{P_2}\\<br />{e}^{2\theta}&=&\frac{P_1}{P_2}=\frac{E_1 I_1}{E_2 I_2}=\frac{Z_{i2}{E_1}^2}{Z_{i1}{E_2}^2}=\frac{Z_{i1}{I_1}^2}{Z_{i2}{I_2}^2}\\<br />{e}^{\theta}&=&\pm\sqrt{{e}^{2\theta}}=\pm\sqrt{\frac{P_1}{P_2}}=\pm\sqrt{\frac{E_1 I_1}{E_2 I_2}}=\pm\sqrt{\frac{Z_{i2}{E_1}^2}{Z_{i1}{E_2}^2}}=\pm\frac{E_1}{E_2}\sqrt{\frac{Z_{i2}}{Z_{i1}}}=\pm\frac{I_1}{I_2}\sqrt{\frac{Z_{i1}}{Z_{i2}}}<br />\end{eqnarray}$ 著者が勝手に定義している式がちゃんと導きだせる。勝手に定義するよりも影像伝搬定数の本来の定義を書けと言いたい。ここでも同様に正負の二つの値が存在するが、受動回路では正極性だけを考える。自然対数関数(ln)と指数関数(e)は互いに逆関数であるというのを忘れていた人はこれを機会に思い出して欲しい。自分も良く判っていなかったのは内緒だ。さて次ぎに著者が示す式も、いきなり結論だけの提示なので、どうやったらそうなるのかついて行けそうもなくなる。 Zi1,Zi2については先の影像インピーダンスの時に導いた式より $\begin{eqnarray}<br />{Z_{i1}}^2&=&\frac{A B}{C D}\\<br />Z_{i1}&=&\pm\sqrt{\frac{A B}{C D}}\\<br />{Z_{i2}}^2&=&\frac{B D}{A C}\\<br />Z_{i2}&=&\pm\sqrt{\frac{B D}{A C}}<br />\end{eqnarray}$ ということでよいが。４端子パラメータA,B,C,Dのみで影像伝達定数θを表すにはどうすんだ。 E1/E2とI1/I2の式を導いて先の伝達定数の式に代入すればよさそうである。実はE1/E2,I1/I2は既に学んだ４端子パラメータの関係式より導くことができる。 $\begin{eqnarray}<br />E_1&=&A E_2+B I_2\\<br />&=&A E_2+B \frac{E_2}{Z_{i2}}\\<br />\frac{E_1}{E_2}&=&A+\frac{B}{Z_{i2}}<br />I_1&=&C E_2+D I_2\\<br />&=&C Z_{i2}I_2+D I_2\\<br />\frac{I_1}{I_2}&=&C Z_{i2}+D<br />\end{eqnarray}$ これを先のθの式に代入すると $\begin{eqnarray}<br />\theta&=&\frac{1}{2}\ln\frac{P_1}{P_2}\\<br />&=&\ln\sqrt{\frac{P_1}{P_2}}\\<br />&=&\ln\sqrt{\frac{E_1 I_1}{E_2 I_2}}\\<br />&=&\ln\sqrt{\left(A+\frac{B}{Z_{i2}}\right)\left(C Z_{i2}+D\right)}\\<br />&=&\ln\sqrt{A C Z_{i2}+A D+B C+\frac{B D}{Z_{i2}}}<br />\end{eqnarray}$ 更に先に求めたZi2の式を代入すると $\begin{eqnarray}<br />\theta&=&\ln\sqrt{A C Z_{i2}+A D+B C+\frac{B D}{Z_{i2}}}\\<br />&=&\ln\sqrt{A C \sqrt{\frac{B D}{A C}}+A D+B C+\frac{B D}{\sqrt{\frac{B D}{A C}}}}\\<br />&=&\ln\sqrt{\sqrt{A B C D}+A D+B C+\sqrt{A B C D}}\\<br />&=&\ln\sqrt{A D+2\sqrt{A B C D}+B C}\\<br />&=&\ln\sqrt{\left(\sqrt{A D}+\sqrt{B C}\right)^2}\\<br />&=&\ln\left(\sqrt{A D}+\sqrt{B C}\right)<br />\end{eqnarray}$ ということになる。なんだ簡単じゃないか(´∀` ) 対称回路の場合にはA=Dとなり、４端子パラメータは実質A,B,Cの３つの独立パラメータから成り $\begin{eqnarray}<br />Z_{i1}&=&Z_{i2}=\sqrt{\frac{B}{C}}\\<br />\theta&=&\ln\left(A+\sqrt{B C}\right)<br />\end{eqnarray}$ ということになる。しかしまたしても次ぎに試練が待っていた。今度は逆にA,B,C,DをZi1,Zi2,θで表せと。しかも著者の示す結論にはまたしても宿敵の双曲線関数が出てくるし、どうすんだこれ。これに関しては以前に紹介した電気回路の古書「第１級無線技術士用　電気回路（下巻）」に詳しい。それを参考に解いてみよう。最初に伝達定数の関係を指数関数で表すと $\begin{eqnarray}<br />{e}^{\theta}&=&\sqrt{A D}+\sqrt{B C}<br />\end{eqnarray}$ またこの逆数も求めておく $\begin{eqnarray}<br />\frac{1}{{e}^{\theta}}&=&{e}^{-\theta}\\<br />&=&\frac{1}{\sqrt{A D}+\sqrt{B C}}\\<br />&=&\frac{\sqrt{A D}-\sqrt{B C}}{\left(\sqrt{A D}+\sqrt{B C}\right)\left(\sqrt{A D}-\sqrt{B C}\right)}\\<br />&=&\frac{\sqrt{A D}-\sqrt{B C}}{A D-B C}\\<br />&=&\sqrt{A D}-\sqrt{B C}<br />\end{eqnarray}$ ここで線形受動回路では相反定理が成り立つのでAD-BC=1となること利用している。ここまで出そろうと複素双曲線関数の登場 $\begin{eqnarray}<br />\sinh\,\theta&=&\frac{{e}^{\theta}-{e}^{-\theta}}{2}\\<br />&=&\frac{\cancel{\sqrt{A D}}+\sqrt{B C}-\left(\cancel{\sqrt{A D}}-\sqrt{B C}\right)}{2}\\<br />&=&\sqrt{B C}\\<br />\cosh\,\theta&=&\frac{{e}^{\theta}+{e}^{-\theta}}{2}\\<br />&=&\frac{\sqrt{A D}+\cancel{\sqrt{B C}}+\left(\sqrt{A D}-\cancel{\sqrt{B C}}\right)}{2}\\<br />&=&\sqrt{A D}<br />\end{eqnarray}$ これは複素双曲線関数と指数関数の以下の関係からも自明である。 $\begin{eqnarray}<br />{e}^{\theta}&=&\cosh\,\theta+\sinh\,\theta\\<br />&=&\sqrt{A D}+\sqrt{B C}\\<br />{e}^{-\theta}&=&\cosh\,\theta-\sinh\,\theta\\<br />&=&\sqrt{A D}-\sqrt{B C}<br />\end{eqnarray}$ 先に導いておいたZi1,Zi2の４端子パラメータ表現からZi1*Zi2とZi1/Zi2の関係を導くと $\begin{eqnarray}<br />Z_{i1}Z_{i2}&=&\sqrt{\frac{\cancel{A} B}{C \cancel{D}}}\sqrt{\frac{B \cancel{D}}{\cancel{A} C}}\\<br />&=&\frac{B}{C}<br />\frac{Z_{i1}}{Z_{i2}}&=&\frac{\sqrt{\frac{A \cancel{B}}{\cancel{C} D}}}{\sqrt{\frac{\cancel{B} D}{A \cancel{C}}}}\\<br />&=&\frac{A}{D}<br />\end{eqnarray}$ これらの４式を以下の様に組み合わせることで４端子パラメータをZi1,Zi2,θで表すことができる $\begin{eqnarray}<br />A&=&\sqrt{\frac{A}{D}}\sqrt{A D}\\<br />&=&\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta\\<br />B&=&\sqrt{\frac{B}{C}}\sqrt{B C}\\<br />&=&\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta\\<br />C&=&\sqrt{\frac{C}{B}}\sqrt{B C}\\<br />&=&\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta\\<br />D&=&\sqrt{\frac{D}{A}}\sqrt{A D}\\<br />&=&\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta<br />\end{eqnarray}$ できたじゃないか(´∀` ) 従って対称回路ではA=D,Zi=Zi1=Zi2が成り立つので４端子パラメータはそれぞれ $\begin{eqnarray}<br />A&=&D=\cosh\,\theta\\<br />B&=&Z_{i}\sinh\,\theta\\<br />C&=&\frac{1}{Z_{i}}\sinh\,\theta\\<br />\end{eqnarray}$ と表される。これでやっと影像パラメータで二端子対回路を表すことができる $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />&=&\left[\begin{array}<br />\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta & \sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta\\<br />\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta & \sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ 対称回路では $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />\cosh\,\theta & Z_{i}\sinh\,\theta\\<br />\frac{1}{Z_{i}}\sinh\,\theta & \cosh\,\theta<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。実はこれ後に学ぶ分布定数回路の伝送路の二端子対回路表現とまったく相似な式となっている。摩訶不思議である。影像パラメータはどの参考書を読んでも判りづらかったけど、判ってしまえば面白い。以前一端子対回路で途中で投げてしまったインピーダンス関数がcoth(s)となる回路の合成問題の解決の糸口がどうやらつかめそうである。それは後日分布定数回路をマスターしてからのお楽しみにしよう。ところで著者はもうひとつ終端開放インピーダンス(Zo1,Zo2)と終端短絡インピーダンス(Zs1,Zs2)による関係式を示しているのだが、どうやったらそれが導けるのかわからない。おそらく、ここまでの結果からだと、伝達定数θが結局４端子パラメータから計算することになってしまうので別の測定可能なパラメータでθを表す必要があるのは確かなのだ。最初の方で導いたZo1,Zo2,Zs1,Zs2を影像パラメータ表現で表すと $\begin{eqnarray}<br />Z_{o1}&=&\frac{A}{C}\\<br />&=&\frac{\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta}{\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta}\\<br />&=&Z_{i1}\coth\,\theta\\<br />Z_{o2}&=&\frac{D}{C}\\<br />&=&\frac{\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta}{\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta}\\<br />&=&Z_{i2}\coth\,\theta\\<br />Z_{s1}&=&\frac{B}{D}\\<br />&=&\frac{\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta}{\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta}\\<br />&=&Z_{i1}\tanh\,\theta\\<br />Z_{s2}&=&\frac{B}{A}\\<br />&=&\frac{\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta}{\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta}\\<br />&=&Z_{i2}\tanh\,\theta<br />\end{eqnarray}$ 従って $\begin{eqnarray}<br />\sqrt{\frac{Z_{o1}}{Z_{s1}}}&=&\sqrt{\frac{Z_{i1}\coth\,\theta}{Z_{i1}\tanh\,\theta}}\\<br />&=&\coth\,\theta<br />\sqrt{\frac{Z_{o2}}{Z_{s2}}}&=&\sqrt{\frac{Z_{i2}\coth\,\theta}{Z_{i2}\tanh\,\theta}}\\<br />&=&\coth\,\theta<br />\end{eqnarray}$ ううむ、わからない。またしても宿敵のcoth関数が出てきたところで、見当違いな方向に進んでいることは間違いない。著者の記述を良く読むと、式の中に出てくるインピーダンスとアドミッタンスはそれぞれインピーダンス行列とアドミッタンス行列に由来するもののようだ。どれにしても同じようなものだと思うのだが。著者の用いているZパラメータはそれぞれFパラメータと影像パラメータで表すと $\begin{eqnarray}<br />Z_{1f}&=&Z_{11}\\<br />&=&\left.\frac{E_1}{I_1}\right\|_{I_2=0}\\<br />&=&\frac{A}{C}\\<br />&=&Z_{i1}\coth\,\theta\\<br />&=&Z_{o1}\\<br />Z_{1s}&=&\frac{1}{Y_{11}}\\<br />&=&\left.\frac{E_1}{I_1}\right\|_{E_2=0}<br />&=&\frac{B}{D}\\<br />&=&Z_{i1}\tanh\,\theta\\<br />&=&Z_{s1}\\<br />Z_{2f}&=&Z_{22}\\<br />&=&\left.\frac{E_2}{I_2}\right\|_{I_1=0}\\<br />&=&\frac{D}{C}\\<br />&=&Z_{i2}\coth\,\theta\\<br />&=&Z_{o2}\\<br />Z_{2s}&=&\frac{1}{Y_{22}}\\<br />&=&\left.\frac{E_2}{I_2}\right\|_{E_1=0}\\<br />&=&\frac{B}{A}\\<br />&=&Z_{i2}\tanh\,\theta<br />&=&Z_{s2}<br />\end{eqnarray}$ 従ってこれから著者の以下の式が成り立つことまでは良い $\begin{eqnarray}<br />Z_{01}&=&\sqrt{\frac{A B}{C D}}=\sqrt{\frac{Z_{11}}{Y_{11}}}=\sqrt{Z_{1f}Z_{1s}}\\<br />Z_{02}&=&\sqrt{\frac{D B}{C A}}=\sqrt{\frac{Z_{22}}{Y_{22}}}=\sqrt{Z_{2f}Z_{2s}}<br />\end{eqnarray}$ 問題は著者が結論として示す以下の関係式 $\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}=\sqrt{Z_{11}Y_{11}}=\sqrt{Z_{22}Y_{22}}=\sqrt{\frac{Z_{1f}}{Z_{2s}}}=\sqrt{\frac{Z_{2f}}{Z_{2s}}}<br />\end{eqnarray}$ どうも成り立っていないように思えるのだが。以下の様だったら問題ないのだが $\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}\\<br />\coth\,\theta&=&\sqrt{Z_{11}Y_{11}}=\sqrt{Z_{22}Y_{22}}=\sqrt{\frac{Z_{1f}}{Z_{2s}}}=\sqrt{\frac{Z_{2f}}{Z_{2s}}}<br />\end{eqnarray}$ まさか著者がcoshとcothを混同して式を一緒にしてしまったのではあるまいか？　ということで著者の誤記という結論にしておこう。対称回路の場合、伝達定数は $\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}\\<br />&=&A=D<br />\end{eqnarray}$ P.S 国内の参考書では、上記の様に入出力電力比の対数から入っているのは小数派で、何故か手間をかけて入出力電圧比と入出力電流比を先に導いて、最終的に伝達定数（入出力電力比）を導き出す回りくどい解説をしているものが手元の古い本で共通に見られた。現在も売られている電気学会編の「電気工学ハンドブック」は酷いことに電圧と電流の伝達定数は示すものの電力に関する伝達定数は出てこない。なにかこの辺に影像パラメータが廃れた原因の一端があるように見える。 P.S 今頃よく見たら最初の影像インピーダンスの説明で、駆動点インピーダンスの説明が間違っていた...orz

webadm	投稿日時: 2010-5-14 12:08
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	反復パラメータ影像パラメータと似て非なる反復パラメータ。ものの本によっては最初に反復パラメータが説明されて、その後に影像パラメータが説明されている。おんなじじゃんヽ(`Д´)ﾉと一瞬思ったけど、実際はまったく違ってた。違いを十分意識するところから始めないといけない。（１）反復インピーダンス(iteration impedance) 二端子対回路の端子対2-2'にZk1を接続した状態で、端子対1-1'から見た駆動点インピーダンスが同じZk1となるZk1を反復インピーダンス(iterative impedance)と呼ぶ。同じ回路で逆に端子対1-1'にZk2を接続した状態で、端子対2-2'から見た駆動点インピーダンスが同じZk2となるZk2も反復インピーダンスである。４端子対パラメータでそれぞれの反復インピーダンスを表すと $\begin{eqnarray}<br />Z_{k1}&=&\frac{E_1}{I_1}=\frac{E_2}{I_2}\\<br />&=&\frac{A E_2 + B I_2}{C E_2+D I_2}\\<br />&=&\frac{A Z_{k1} I_2+B I_2}{C Z_{k1} I_2+D I_2}\\<br />&=&\frac{A Z_{k1}+B}{C Z_{k1}+D}<br />\end{eqnarray}$ $\begin{eqnarray}<br />Z_{k1}\left(C Z_{k1}+D\right)-A Z_{k1}-B&=&C {Z_{k1}}^2+\left(D-A\right)Z_{k1}-B\\<br />&=&{Z_{k1}}^2+\frac{\left(D-A\right)Z_{k1}}{C}-\frac{B}{C}\\<br />&=&\left(Z_{k1}+\frac{D-A}{2 C}\right)^2-\left(\frac{B}{C}+\left(\frac{D-A}{2 C}\right)^2\right)\\<br />&=&\left(Z_{k1}+\frac{D-A}{2 C}+\sqrt{\frac{B}{C}+\left(\frac{D-A}{2 C}\right)^2}\right)\left(Z_{k1}+\frac{D-A}{2 C}-\sqrt{\frac{B}{C}+\left(\frac{D-A}{2 C}\right)^2}\right)\\<br />&=&\left(Z_{k1}+\frac{D-A+\sqrt{\left(D-A\right)^2+4 B C}}{2 C}\right)\left(Z_{k1}+\frac{D-A-\sqrt{\left(D-A\right)^2+4 B C}}{2 C}\right)\\<br />&=&0\\<br />Z_{k1}&=&\frac{A-D\mp\sqrt{\left(A-D\right)^2+4 B C}}{2 C}<br />\end{eqnarray}$ 受動回路ではインピーダンスの実数部は常に正のみ扱うので $\begin{eqnarray}<br />Z_{k1}&=&\frac{A-D+\sqrt{\left(A-D\right)^2+4 B C}}{2 C}<br />\end{eqnarray}$ ということになる。 Zk2について同様に導くと、Fi行列なのでAとDが逆になるだけなので $\begin{eqnarray}<br />Z_{k2}&=&\frac{D-A+\sqrt{\left(D-A\right)^2+4 B C}}{2 C}<br />\end{eqnarray}$ ということになる。対称回路ではA=Dとなるので $\begin{eqnarray}<br />Z_{k1}&=&\frac{\cancel{A-D}+\sqrt{\cancel{\left(A-D\right)^2}+\cancel{4} B C}}{\cancel{2} C}\\<br />&=&\sqrt{\frac{B}{C}}<br />Z_{k2}&=&\frac{\cancel{D-A}+\sqrt{\cancel{\left(D-A\right)^2}+\cancel{4} B C}}{\cancel{2} C}\\<br />&=&\sqrt{\frac{B}{C}}<br />\end{eqnarray}$ ということになる。以下の様に同一の反復インピーダンスを持つ回路をいくつ縦列接続した場合でも、全体の回路が同じ反復インピーダンスを持つことになる。これが反復(iterative)と呼ばれる由来であると思われる。このことから一様伝送路（分布定数回路）では反復インピーダンスは特性インピーダンスと同じ意味になる。一方集中定数回路では回路固有で非対称回路では方向によっても異なるので反復インピーダンスなる用語で区別する必要があるのだろう。（２）反復伝搬定数(iterative propagation constant) 影像パラメータの影像伝達定数と似て非なる反復パラメータの反復伝搬定数。伝達と伝搬の違いがある。どうやら伝搬定数なる用語は電信ケーブルや電話ケーブルなどの一様伝送路（分布定数回路）から持ってきたように見える。分布定数回路では入力端子対と出力端子対の間の距離に依存するが、集中定数回路は端子対の間の距離は理屈の上では存在しないので、回路網によって一意に決定される定数となる。反復伝搬定数は以下の通り、先に反復インピーダンスを導いた時の関係,E1/E2=I1/I2により電圧、電流に対しても $\begin{eqnarray}<br />\gamma&=&\frac{1}{2}\ln\frac{P_1}{P_2}=\frac{1}{2}\ln\frac{E_1 I_1}{E_2 I_2}\\<br />&=&\frac{1}{2}\ln\frac{{E_1}^2}{{E_2}^2}=\frac{1}{2}\ln\frac{{I_1}^2}{{I_2}^2}\\<br />&=&\ln\frac{E_1}{E_2}=\ln\frac{I_1}{I_2}\\<br />{e}^{\gamma}&=&\frac{E_1}{E_2}=\frac{I_1}{I_2}<br />\end{eqnarray}$ と定義される。ここで先の反復インピーダンスで用いた関係式より $\begin{eqnarray}<br />I_1&=&C E_2+D I_2=C Z_{k1}I_2+D I_2\\<br />{e}^{\gamma}&=&\frac{I_1}{I_2}=C Z_{k1}+D\\<br />&=&\cancel{C}\frac{A-D+\sqrt{\left(A-D\right)^2+4 B C}}{2\cancel{C}}+D\\<br />&=&\frac{A-\cancel{D}+\sqrt{\left(A-D\right)^2+4 B C}+\cancel{2} D}{2}\\<br />&=&\frac{A+D+\sqrt{\left(A-D\right)^2+4 B C}}{2}\\<br />&=&\frac{A+D}{2}+\sqrt{\frac{A^2-2 A D+D^2+4 B C}{4}}\\<br />&=&\frac{A+D}{2}+\sqrt{\frac{A^2+2 A D+D^2-4\left(A D-B C\right)}{4}}\\<br />&=&\frac{A+D}{2}+\sqrt{\left(\frac{A+D}{2}\right)^2-1}<br />\end{eqnarray}$ ということになる。ここでも線形回路の相反定理、AD-BC=1を利用した。一方上記の逆数は $\begin{eqnarray}<br />{e}^{-\gamma}&=&\frac{1}{{e}^{\gamma}}\\<br />&=&\frac{1}{\frac{A+D}{2}+\sqrt{\left(\frac{A+D}{2}\right)^2-1}}\\<br />&=&\frac{\frac{A+D}{2}-\sqrt{\left(\frac{A+D}{2}\right)^2-1}}{\left(\frac{A+D}{2}+\sqrt{\left(\frac{A+D}{2}\right)^2-1}\right)\left(\frac{A+D}{2}-\sqrt{\left(\frac{A+D}{2}\right)^2-1}\right)}\\<br />&=&\frac{\frac{A+D}{2}-\sqrt{\left(\frac{A+D}{2}\right)^2-1}}{\cancel{\left(\frac{A+D}{2}\right)^2}-\cancel{\left(\frac{A+D}{2}\right)^2}+1}\\<br />&=&\frac{A+D}{2}-\sqrt{\left(\frac{A+D}{2}\right)^2-1}<br />\end{eqnarray}$ 従って伝搬定数を双曲線関数で表すと $\begin{eqnarray}<br />\cosh\,\gamma&=&\frac{{e}^{\gamma}+{e}^{-\gamma}}{2}\\<br />&=&\frac{\frac{A+D}{2}+\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}+\frac{A+D}{2}-\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{2}\\<br />&=&\frac{A+D}{2}<br />\end{eqnarray}$ ということになる。また対称回路の場合A=Dなので、伝搬定数は $\begin{eqnarray}<br />\cosh\,\gamma&=&\frac{A+D}{2}\\<br />&=&A=D\\<br />&=&\cosh\,\theta\\<br />\gamma&=&\cosh^{-1}\,A=\theta<br />\end{eqnarray}$ 対称回路の影像パラメータと同値となる。最後に４端子パラメータを反復パラメータで表してみよう。最初に準備として $\begin{eqnarray}<br />\sinh\,\gamma&=&\frac{{e}^{\gamma}-{e}^{-\gamma}}{2}\\<br />&=&\frac{\cancel{\frac{A+D}{2}}+\sqrt{\left(\frac{A+D}{2}\right)^2-1}-\cancel{\frac{A+D}{2}}+\sqrt{\left(\frac{A+D}{2}\right)^2-1}}{2}\\<br />&=&\sqrt{\left(\frac{A+D}{2}\right)^2-1}\\<br />Z_{k1}-Z_{k2}&=&\frac{A-D+\cancel{\sqrt{\left(A-D\right)^2+4 B C}}}{2 C}-\frac{D-A+\cancel{\sqrt{\left(D-A\right)^2+4 B C}}}{2 C}\\<br />&=&\frac{A-D}{C}\\<br />Z_{k1}+Z_{k2}&=&\frac{\cancel{A-D}+\sqrt{\left(A-D\right)^2+4 B C}}{2 C}+\frac{\cancel{D-A}+\sqrt{\left(D-A\right)^2+4 B C}}{2 C}\\<br />&=&\frac{\sqrt{\left(D-A\right)^2+4 B C}}{C}\\<br />&=&\frac{\sqrt{D^2-2 A D+A^2+4 B C}}{C}\\<br />&=&\frac{\sqrt{D^2+2 A D+A^2-4\left(A D- B C\right)}}{C}\\<br />&=&\frac{\sqrt{\left(A+D\right)^2-4}}{C}\\<br />&=&\frac{2\sqrt{\left(\frac{A+D}{2}\right)^2-1}}{C}\\<br />Z_{k1}Z_{k2}&=&\left(\frac{A-D+\sqrt{\left(A-D\right)^2+4 B C}}{2 C}\right)\left(\frac{D-A+\sqrt{\left(D-A\right)^2+4 B C}}{2 C}\right)\\<br />&=&\frac{\left(A-D\right)\left(D-A+\sqrt{\left(D-A\right)^2+4 B C}\right)+\sqrt{\left(A-D\right)^2+4 B C}\left(D-A+\sqrt{\left(D-A\right)^2+4 B C}\right)}{4 C^2}\\<br />&=&\frac{-\cancel{\left(D-A\right)^2}+\cancel{\left(A-D\right)\sqrt{\left(D-A\right)^2+4 B C}}-\cancel{\left(A-D\right)\sqrt{\left(A-D\right)^2+4 B C}}+\cancel{\left(D-A\right)^2}+4 B C}{4 C^2}\\<br />&=&\frac{B}{C}<br />\end{eqnarray}$ これらの関係から、４端子パラメータはそれぞれ $\begin{eqnarray}<br />A&=&\frac{A+\cancel{D}}{2}+\frac{\frac{A-\cancel{D}}{\cancel{C}}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{\frac{2\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{\cancel{C}}}\\<br />&=&\cosh\,\gamma+\frac{Z_{k1}-Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma\\<br />B&=&\frac{\cancel{2}\frac{B}{\cancel{C}}}{\frac{\cancel{2}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{\cancel{C}}}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}\\<br />&=&\frac{2Z_{k1}Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma\\<br />C&=&\frac{\cancel{2}}{\frac{\cancel{2}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{C}}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}\\<br />&=&\frac{2}{Z_{k1}+Z_{k2}}\sinh\,\gamma\\<br />D&=&\frac{\cancel{A}+D}{2}-\frac{\frac{\cancel{A}-D}{\cancel{C}}}{\frac{2\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}}{\cancel{C}}}\cancel{\sqrt{\left(\frac{A+D}{2}\right)^2-1}}\\<br />&=&\cosh\,\gamma-\frac{Z_{k1}-Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma<br />\end{eqnarray}$ ということになり、行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\cosh\,\gamma+\frac{Z_{k1}-Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma & \frac{2Z_{k1}Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma\\<br />\frac{2}{Z_{k1}+Z_{k2}}\sinh\,\gamma & \cosh\,\gamma-\frac{Z_{k1}-Z_{k2}}{Z_{k1}+Z_{k2}}\sinh\,\gamma<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。対称回路ではZk1=Zk2=Zkであることから $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />\cosh\,\gamma & Z_{k}\sinh\,\gamma\\<br />\frac{1}{Z_{k}}\sinh\,\gamma & \cosh\,\gamma<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\cosh\,\theta & Z_{i}\sinh\,\theta\\<br />\frac{1}{Z_{i}}\sinh\,\theta & \cosh\,\theta<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。従って対称回路では影像パラメータと同値。やっぱり、おんなじじゃんヽ(`Д´)ﾉ P.S 影像パラメータの時もそうだったけど、四端子パラメータ,A,B,C,Dを影像パラメータ(Zi1,Zi2,Θ)や反復パラメータ(Zk1,Zk2,γ)で表す解を求めるのにヒューリスティックな思考錯誤で行ったが、結果的に解はすべてパラメータ、パラメータのべき根、実数係数、虚数単位(j)、それらの間の任意の加減乗除（多項式）で表されている。理数系から見れば「当たり前じゃん、ばーか、ばーか」と工学系は頭悪いという口実を与えてしまう。さすがに代数的に解くのは読者の課題としようとは、今回は言わない。代数多様体上の有理点を求める問題だからである。高額な数式処理ソフトなら自動的に解けるかもしれないが、人間が有限の種類の積み木やレゴを複数組み合わせて目的の構造を作る組み合わせを思考錯誤で見出した方が早いかもしれない。戦前にCauerはフィルタ回路合成問題が代数多様体上の有理点を求める数論的代数幾何学の問題と同値であることを明らかにしたが、当時代数多様体を研究していたのはドイツぐらいだったのと枢軸国だったので連合国で理解されたのは戦後になってからである。戦前にドイツやフランスの先端数学者から血脈を受け継いでいた日本人数学者の師弟が戦後になって次々と先駆的な仕事をしたが、工学との接点は他国に比べて皆無に近いのは何度も言うが残念である。読者も挑戦するのは構わないが、近代数学の世界にどっぷり浸かる必要があるので、本来の問題に数年内に戻ってこれるかどうか。そっち（数学）の方で興味ある問題を見つけてしまって数学者になってしまう可能性も無きにしも非ず。いずれ誰か２つの世界の間を往復して便りをくれるものと期待しよう。

webadm	投稿日時: 2010-5-16 3:48
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	理想変成器変成器は上巻の交流回路理論で相互誘導回路のときに基本を学んでいる。大抵の本はその時に一緒に理想変成器にも触れているのだが、著者はあえて交流回路の基礎では触れずに、フィルタ理論の準備である二端子対回路で登場させたのは理由がある。著者は書いていなかったが、二端子対の並列接続の際に、完全４端子回路と実質３端子対回路同士だと端子対条件を満たさなくなるためアドミッタンス行列の重ね合わせが成り立たない。それを回避するにはいずれかの端子対に理想変成器を挿入する必要があった。戦前のフィルタ設計ではどうしても完全４端子回路と３端子回路を並列接続する際には端子対条件を満たすために理想変成器を含めた回路で実現しなければならなかった。理想と名前がついているぐらいだから、現実の変成器とは違うのだろう。ところで、どこが違うのだろうか？著者は詳しく理想変成器の特徴を述べていないが、手元の電気学会編「電気工学ハンドブック」には詳しく説明されている。 "[2]理想変成器　密結合変成器においてインダクタンスを無限大にした（磁心の透磁率を無限大にしたと考えてもよい）極限は理想変成器と呼ばれ..." とある。なるほど現実にはありそうもない。ここで密結合変成器というのは、結合係数kが1である変成器のことである。結合係数kの定義から、 $\begin{eqnarray}<br />k&=&\frac{M}{\sqrt{L_1 L_2}}=1\\<br />M^2&=&L_1 L_2<br />\end{eqnarray}$ という関係が成り立つことを意味する。あれ、著者の言う変成比:nがどこにも出てこないな。上巻を見ても変成器のところには出てこない。だめじゃん(;´Д`) ということで変成比:nでいきなり躓く。著者から詳しく触れない理由は、電磁気学理論に足を踏み入れないと説明できないのと、かなり式が出てくるので紙面を食ってしまうという判断からだろう。ここではとりあえず、前出の「電気工学ハンドブック」にある理想変成器の巻数比:nの関係式を挙げるにとどめよう。理想変成器の一次側端子対1-1'の電圧をV1,端子対2-2'の電圧をV2とし、端子対1-1'に流れる電流をI1,端子対2-2'に流れる電流をI2とすると以下の関係が成り立つ $\begin{eqnarray}<br />V_1&=&\frac{V_2}{n}\\<br />I_1+n I_2&=&0<br />\end{eqnarray}$ 一次側の電圧の巻線比:n倍が二次側の電圧となる。逆に二次側の電流は一次側の1/nになるというもの。 I2の電流の方向が逆だが、４端子対パラメータで表すと $\begin{eqnarray}<br />\left[\begin{array}<br />V_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{n} & 0\\<br />0 & n<br />\end{array}\right]\left[\begin{array}<br />V_2\\<br />-I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。それと著者は触れていないが、「電気工学ハンドブック」には理想変成器のインピーダンス変換機能について記述がある。理想変成器の二次側にインピーダンスZを接続した場合、一次側からみた駆動点インピーダンスZinは $\begin{eqnarray}<br />Z_{in}&=&\frac{V_1}{I_1}\\<br />&=&\frac{\frac{V_2}{n}}{-n I_2}\\<br />&=&\frac{\frac{-Z I_2}{n}}{-n I_2}\\<br />&=&\frac{Z}{n^2}<br />\end{eqnarray}$ ということで巻線比の二乗分の１に変換される。

webadm	投稿日時: 2010-5-16 5:27
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3086	理想ジャイレータ次ぎは理想ジャイレータところでジャイレータってなんじゃいれーた。調べてみると戦後すぐにオランダPhilipsの技術者Tellegenによって抵抗、キャパシタ、インダクタそれに理想変成器に続く５番目の非可逆線形受動素子として提案された。ジャイレータは内部に２つの独立した制御電源を持つ以下のような等価回路として表すことが出来る。 V1,I1,V2,I2に関して以下の関係が成り立つ。 $\begin{eqnarray}<br />I_1&=&G_2 V_2\\<br />I_2&=&-G_1 V_1<br />\end{eqnarray}$ 一方の端子対に流れる電流が他方の端子対の電圧に比例する。あるいは一方の端子対に加わる電圧と他方の端子対に流れる電流が比例する。縦続行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />V_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />0 & \frac{1}{G_1}\\<br />G_2 & 0<br />\end{array}\right]\left[\begin{array}<br />V_2\\<br />-I_2<br />\end{array}\right]<br />\end{eqnarray}$ 電流の向きを縦続行列のそれと同じにして、G1=G2=1/Rと置くと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />0 & R\\<br />\frac{1}{R} & 0<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ 著者の式と同じになる。Tellegenは図のような回路シンボルまで合わせて提案しており、現在もそれが使われている。おそらく内部の２つの独立した制御電源がちらりと見えているイメージだろう。内部にコンダクタンス(G)を持つように見えて、実は内部では電力を消費しない。一方から供給される電力は他方にそのまま損失なく伝達される。内部に供給される電力から出力される電力を差し引くと $\begin{eqnarray}<br />P&=&P_{in}-P_{out}=V_1 I_1-V_2 I_2\\<br />&=&R I_2 I_1-R I_1 I_2\\<br />&=&0<br />\end{eqnarray}$ と内部に蓄積されたり消費される電力は0である。著者は現実のジャイレータがHall効果やFaraday効果を利用するものや能動回路を用いても構成出来るとしているが、前者はサーキュレータやアイソレータと呼ばれるマイクロ波で用いられる受動素子のことだと思われ、厳密にはジャイレータは受動素子では実現できないのでそれとは違う。後者の能動素子回路が現実のジャイレータの実現方法である。現実のジャイレータは能動素子(真空管、トランジスタ、オペアンプ）を用いて一般化インピーダンス変換器(Generalized Impedance Converter:GIC)を実現するのが目的。一般化インピーダンス変換器とは何かというと、インピーダンスを逆にする回路のこと。例えば理想ジャイレータの一方の端子対をキャパシタで終端した場合、他方の端子対から見た駆動点インピーダンスを求めると $\begin{eqnarray}<br />E_1&=&R I_2\\<br />&=& R E_2 C s\\<br />I_1&=&\frac{E_2}{R}\\<br />Z_{in}&=&\frac{E_1}{I_1}\\<br />&=&\frac{R \cancel{E_2} C s}{\frac{\cancel{E_2}}{R}}\\<br />&=&R^2 C s\\<br />&=&L s\\<br />L&=&R^2 C\,[H]<br />\end{eqnarray}$ ということになり、見事にキャパシタンスを使ってインダクタンス回路を実現できることになる。キャパシタンスのジャイレータ比の二乗倍のインダクタンスがつながっているように見えることになる。一番有益なのがリアクタンスの変換で、低周波フィルタ回路を実現する上で大きな値のインダクタンスが必要になるが、それをキャパシタンスをGICでインピーダンス変換しインダクタンスとして見せることによってコイルを一切使わずにフィルタ回路が構成できることになる。コイルは大きいし、重いし、誘導ノイズを受けやすいし、無いにこしたことはない。 GICはオペアンプと外付け部品(抵抗とコンデンサ）だけで実現できるので、アナログ回路やアナログICでは不可欠な回路要素となっている。理想ジャイレータを第五の受動素子として加えることによって、戦後更に広範囲なフィルタが実現方法が考案されていったという経緯がある。ちなみにTellegenという人は、他にも真空管の４極管の問題を解消した５極管を発明者、回路網理論のTellegenの定理でも有名。詳しくはフィルタ理論に譲ることにする。

(1) 2 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を