| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-8-7 12:03 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【1】波形補間 最初にいきなり興味深い問題が出てくる。やはり著者はFourier変換の現実的な応用面を知っていて、それと関連のある問題を考えているのかもしれない。
最初の問題は、y(t)=a1*sin(ωt)+b0+b1*cos(ωt) という関数を用いて、以下の電圧波形e(t)を近似しようとするときに、t=0,π/ω,3π/2ωの3点でy(t)とe(t)が一致するには、係数a1,b0,b1をどのようにすればよいかというもの。 e(t)=2t, 0≦t≦2π/ω これはどういう意味だろう。y(t)はFourier級数なので繰り返し波形になる。 e(t)をプロットすると 式としては連続関数として与えられているが、近似関数に対しては3点が離散的な数列として与えられているだけである。 こうした離散的な数列と一致する関数を合成することを波形補間とも呼ぶ。 デジタルオシロのように離散的にサンプリングされた波形データを滑らかに曲線で表示するにはなんらかの波形補間が必要である。 画像イメージを拡大表示する際も素の画素データ列が離散的に離ればなれになるため隙間の画素データを補間しないといけない。 もちろん素のデータは離散数値列なので、その間の情報は無いのだが、ほとんどの波形はFourier級数で近似できるので有限項数のFourier級数の係数を求めれば良いことになる。 そのためには問題で与えられているe(t)の式は一端忘れて、与えられた3点の値のみがわかっているものとする必要がある。 再びそれを図に描くと これは有る意味で方程式の解を求める問題でもある。微分方程式程面倒ではない。 3点(t0,t1,t2)でそれぞれ以下の関係式がなりたたねばならない。 y(t0)=a1*sin(ω*t0)+b0+b1*cos(ω*t0)=2*t0 y(t1)=a1*sin(ω*t1)+b0+b1*cos(ω*t1)=2*t1 y(t2)=a1*sin(ω*t2)+b0+b1*cos(ω*t2)=2*t2 これをa1,b0,b1に関する三元連立方程式として解くと (%i1) e1:a1*sin(o*t0)+b0+b1*cos(o*t0)=2*t0; (%o1) a1*sin(o*t0)+b1*cos(o*t0)+b0=2*t0 (%i2) e2:a1*sin(o*t1)+b0+b1*cos(o*t1)=2*t1; (%o2) a1*sin(o*t1)+b1*cos(o*t1)+b0=2*t1 (%i3) e3:a1*sin(o*t2)+b0+b1*cos(o*t2)=2*t2; (%o3) a1*sin(o*t2)+b1*cos(o*t2)+b0=2*t2 (%i4) solve([e1,e2,e3],[a1,b0,b1]); (%o4) [[a1=- (t0*(2*cos(o*t2)-2*cos(o*t1))-2*t1*cos(o*t2)+2*cos(o*t1)*t2+cos(o*t0)*(2*t1-2*t2))/(cos(o*t0)*(sin(o*t2)-sin(o*t1))-cos(o*t1)*sin(o*t2)+sin(o*t1)*cos(o*t2)+sin(o*t0)*(cos(o*t1)-cos(o*t2))),b0=(t0* (2*sin(o*t1)*cos(o*t2)-2*cos(o*t1)*sin(o*t2))+cos(o*t0)*(2*t1*sin(o*t2)-2*sin(o*t1)*t2)+sin(o*t0)* (2*cos(o*t1)*t2-2*t1*cos(o*t2)))/(cos(o*t0)*(sin(o*t2)-sin(o*t1))-cos(o*t1)*sin(o*t2)+sin(o*t1)* cos(o*t2)+sin(o*t0)*(cos(o*t1)-cos(o*t2))),b1= (t0*(2*sin(o*t2)-2*sin(o*t1))-2*t1*sin(o*t2)+2*sin(o*t1)*t2+sin(o*t0)*(2*t1-2*t2))/(cos(o*t0)*(sin(o*t2)-sin(o*t1))-cos(o*t1)*sin(o*t2)+sin(o*t1)*cos(o*t2)+sin(o*t0)*(cos(o*t1)-cos(o*t2)))]] (%i9) ratsimp(%); (%o9) [[a1=-((2*t1-2*t0)*cos(o*t2)+(2*cos(o*t0)-2*cos(o*t1))*t2+2*t0*cos(o*t1)-2*cos(o*t0)*t1)/(sin(o*t2-o*t1)-sin(o*t2-o*t0)+sin(o*t1-o*t0)),b0= (2*t0*sin(o*t2-o*t1)-2*t1*sin(o*t2-o*t0)+2*sin(o*t1-o*t0)*t2)/(sin(o*t2-o*t1)-sin(o*t2-o*t0)+sin(o*t1-o*t0)),b1= ((2*t1-2*t0)*sin(o*t2)+(2*sin(o*t0)-2*sin(o*t1))*t2+2*t0*sin(o*t1)-2*sin(o*t0)*t1)/(sin(o*t2-o*t1)-sin(o*t2-o*t0)+sin(o*t1-o*t0))]] ということになる。これに t0=0 t1=π/ω t2=3π/2ω を代入すると (%i10) subst(0, t0, [[a1=-((2*t1-2*t0)*cos(o*t2)+(2*cos(o*t0)-2*cos(o*t1))*t2+2*t0*cos(o*t1) -2*cos(o*t0)*t1)/(sin(o*t2-o*t1)-sin(o*t2-o*t0)+sin(o*t1-o*t0)),b0=(2*t0*sin(o*t2 -o*t1)-2*t1*sin(o*t2-o*t0)+2*sin(o*t1-o*t0)*t2)/(sin(o*t2-o*t1)-sin(o*t2-o*t0)+sin(o*t1 -o*t0)),b1=((2*t1-2*t0)*sin(o*t2)+(2*sin(o*t0)-2*sin(o*t1))*t2+2*t0*sin(o*t1)-2*sin(o*t0)*t1)/(sin(o*t2 -o*t1)-sin(o*t2-o*t0)+sin(o*t1-o*t0))]]); (%o10) [[a1=(-2*t1*cos(o*t2)-(2-2*cos(o*t1))*t2+2*t1)/(sin(o*t2-o*t1)-sin(o*t2)+sin(o*t1)),b0=(2*sin(o*t1)*t2-2*t1*sin(o*t2))/(sin(o*t2-o*t1)-sin(o*t2)+sin(o*t1)),b1= (2*t1*sin(o*t2)-2*sin(o*t1)*t2)/(sin(o*t2-o*t1)-sin(o*t2)+sin(o*t1))]] (%i11) subst(%pi/o, t1, [[a1=(-2*t1*cos(o*t2)-(2-2*cos(o*t1))*t2+2*t1)/(sin(o*t2-o*t1)-sin(o*t2) +sin(o*t1)),b0=(2*sin(o*t1)*t2-2*t1*sin(o*t2))/(sin(o*t2-o*t1)-sin(o*t2)+sin(o*t1)),b1=(2*t1*sin(o*t2) -2*sin(o*t1)*t2)/(sin(o*t2-o*t1)-sin(o*t2)+sin(o*t1))]]); (%o11) [[a1=-(-(2*%pi*cos(o*t2))/o-4*t2+(2*%pi)/o)/(2*sin(o*t2)),b0=%pi/o,b1=-%pi/o]] (%i12) subst(3*%pi/(2*o), t2, [[a1=-(-(2*%pi*cos(o*t2))/o-4*t2+(2*%pi)/o)/(2*sin(o*t2)),b0=%pi/o,b1= -%pi/o]]); (%o12) [[a1=-(2*%pi)/o,b0=%pi/o,b1=-%pi/o]] 従って a1= -2π/ω b0=π/ω b1=-π/ω ということになる。これをy(t)の式に代入してプロットしてみると wxplot2d([-2*%pi*sin(t)-%pi*cos(t)+%pi,2*t], [t,0,2*%pi])$ 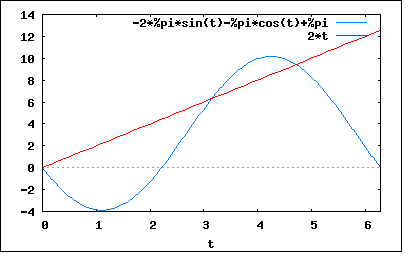 ω=1と置いて2πまでの時間をプロットしたもの。t=0,π,3π/2 の3点でe(t)とy(t)のカーブが一致していることが確認できる。 さすがに項数が少ないと正弦波そのものなので近似とはいいがたいが、確かにサンプル値は一致している。 微分方程式と違って、Fourier級数の場合には係数が与えられるとそれによって唯一の関数が定まる。従ってサンプル数を多くとればそれだけ多くの次数の係数を解くことができより近似な関数が得られるということになる。 実際にはこれはサンプル数が多くなると連立方程式を解くのは大変なことになるので、実用的な波形補完はナイキスト・シャノンのサンプリング定理に基づいて、ナイキストレートによる等間隔に入力信号をサンプルした離散データ列と重み漬け関数(フィルターの伝達関数)をサンプリングした離散データ列とをたたき込み積分する方法が用いられる。詳しくは離散Fourier変換とδ関数、サンプリング定理を学ばないと難しいので割愛。後日「デジタル信号処理理論おもちゃ箱」とかいうボードが出来た暁にはその辺も触れてみたい。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

