ログイン
ユーザ名:

パスワード:


パスワード紛失

新規登録
Main Menu
Tweet
Facebook
Line
:-?
フラット表示 前のトピック | 次のトピック
投稿者 スレッド
webadm
投稿日時: 2009-11-12 1:04
Webmaster
登録日: 2004-11-7
居住地:
投稿: 3084
Cauer展開（連分数展開）
Foster　reactance theoremに対する重要な進展が1927年ドイツ人Wilhelm Cauerによってもたらされた。彼は最初にリアクタンス関数を連分数展開することによって２つの異なる回路構成で表されることに気づいた。

ところで連分数展開ってなんだ？

複素解析の本には部分分数展開の話は出てくるが連分数展開の話はついぞ見かけない。連分数がどんなものかは憶えているが、連分数展開の方法については詳しく知らないのである。そもそも有理型多項式を連分数展開する方法は誰が考えたのだろうか？

そして数学の歴史を知るためにまたしてもタイムマシンに乗らないといけないらしい。連分数は分数や多項式と同様に古くから研究されている数の表現方法である。すべて有理数は有限な連分数で表すことができる、無理数も無限の連分数で表すことができる。無理数を連分数で表すと、べき級数の多項式で表すよりも簡潔で規則性が現れるという不思議な事実も知られている。べき級数で表すと次数が高い項になるにつれ係数の分母や分子や乗数が大きな数となり情報量が増えてしまう。それに対して連分数で表すと、少ない数値と乗数だけで済む。実数をコンパクトに表現するには連分数の方が効率的らしい。コンピューターで使用されている浮動小数点表現はどうなのだろう？　あれは本当に効率的なのだろうか？

すこしばかり数学の領域での連分数についておさらいしてみる必要がありそうである。

有理型関数を連分数展開するには、部分分数展開と同じようにEuclidの互除法を使用する。

Z(s)=\frac{N(s)}{D(s)}=Q_1(s)+\frac{R_1(s)}{D(s)}

deg N(s) > deg D(s)の場合は上記の様に商Q1(s)と剰余R1(s)が得られる。当然deg R1(s) < deg D(s)なのであとは部分分数に展開するしかないと誰もが疑わなかった。Cauerはこれが以下の様に連分数に展開できることを示した。

Z(s)=Q_1(s)+\frac{R_1(s)}{D(s)} \\ &=&Q_1(s)+\frac{1}{\frac{D(s)}{R_1(s)}} \\ &=&Q_1(s)+\frac{1}{Q_2(s)+\frac{R_2(s)}{D(s)}}\end{eqnarray}

剰余項の逆数の逆数は元と同じ、逆数にするとdeg D(s) > deg Rn(s)なので再び商と剰余が得られる。これを剰余が定数になるまで繰り返せばよい。

Z(s)=Q_1(s)+\frac{1}{Q_2(s)+\frac{1}{Q_3(s)+\frac{1}{Q_4(s)+...}}

さて次ぎにこの連分数展開の物理的な意味を議論する必要がある。

Z(s)がインピーダンス関数の場合は、Q1(s)はインピーダンスであり、残りの項もインピーダンスである。従って駆動点から見ると２つのインピーダンスが直列に接続されているように見える。最後のインピーダンスに関してその駆動点から見ると更に２つのアドミッタンスが並列に接続されているように見える。そして更に最後のアドミッタンスは連分数展開されて、２つのインピーダンスが直列に接続されているように見える。それを図に表すと



これを回路的に書き直すと、どっかで見たようなラダー回路を構成することが明らかとなる。これはFoster展開からは想像も出来なかったことである。



これを再び駆動点インピーダンス関数の式として表すと

\begin{eqnarray}Z(s) &=&Z_1(s)+Z_2(s) \\ &=&Z_1(s)+\frac{1}{Y_2(s)+Y_3(s)} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+Z_4(s)}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+Y_5(s)}}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+\frac{1}{Z_5(s)+Z_6(s)}}}} \\ &=&Z_1(s)+\frac{1}{Y_2(s)+\frac{1}{Z_3(s)+\frac{1}{Y_4(s)+\frac{1}{Z_5(s)+\frac{1}{...}}}}}\end{eqnarray}

ということになる。言われてみれば当たり前なのだが、直流回路理論を学んだ時にはこうした発想は思いもつかなかった。まさに数学と電気工学の境界領域に光を照らしたCauerならではである。これほどまでに数学の領域の有理型複素関数と物理的な電気回路の見事なまでの対称性は片方だけで食っていけた専門家には思いも寄らないことだったことが想像に難くない。ナチス一党独裁の下ユダヤ廃絶が極限に高まっていた当時、親戚にユダヤ系が一人居るということだけで教授の肩書きはあっても教職にはつけなけず、民間企業で食いつなぎ、ロックフェラー財団の招きでfellowとして米国に渡ってFosterなどベル研の研究者と出会うことができたのは不幸中の幸いだったのかもしれない。ドイツで何不自由のない教職生活が出来ていたなら我々が知るCauerは存在しなかったのかもしれない。ナチスを称賛するつもりは毛頭ないが、当時ナチスが存在しなければCauerの業績も無かったかもしれない。ナチスとCauerの理論は悪と善のような双対的存在として見ることもできるのはなんとも皮肉である。

話をもとに戻そう。Cauer展開に関してもFoster展開と同様に駆動点インピーダンスの有理型関数をインピーダンス関数あるいはアドミッタンス関数として捉えるか、またそれぞれの極と零点の取り方に関する４つの組み合わせを考察する必要がある。それぞれについてどのような回路構成となるのか興味深いところである。

再び駆動点インピーダンスの式

Z(s)=H \frac{\left(s^2+{\omega_{1}}^2\right)\left(s^2+{\omega_{3}}^2\right)...\left(s^2+{\omega_{2n-1}}^2\right)}{s \left(s^2+{\omega_{2}}^2\right)\left(s^2+{\omega_{4}}^2\right)...\left(s^2+{\omega_{2n-2}}^2\right)}

から出発することにしよう。これを部分分数に展開しても連分数に展開しても関数としての振る舞いはまったく同じでなければならない。

元の駆動点インピーダンスの式は分子の次数が分母の次数よりも１大きいためs=jωと置いた時にω=0を零点、ω=∞に極を持つケースに該当する。

実はここから連分数に展開するところで個人的に立ち止まってしまった。

本書に限らずほとんどの書が最初にω=∞に極を持つ項を商として分離している。

個人的にはもう一つの方法があると思ったのだ。これはFoster展開の式

Z(s)=\frac{h_0}{s}+\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2}+h_\infty{s}

を連分数展開に書き換える場合、以下の３通りがあると個人的に考えたのである。

\begin{eqnarray}Z(s) &=&h_\infty{s}+Z_2(s) \\ Z(s) &=&\frac{h_0}{s}+Z_2(s) \\ Z(s) &=&\frac{h_{2}s}{s^2+{\omega_{2}}^2}+Z_2(s)\end{eqnarray}

本書に限らずどの本も最初の２つのみしか扱わず３番目は登場しない。とりあえず最初は伝統に従って最初の２つを扱い、最後に３番目を時間があれば考えてみることにしよう。

Cauer展開には有理型関数の連分数展開を考えないといけないのは当たり前なのだが、調べてみると連分数はやばい。嵌りそうでやばい。連分数というとRamanujan、Ramanujanというと連分数が出てくる。インド人の若き天才数学者Ramanujanと彼を発掘した英国Cambridge大の純粋数学者G.H.HardyはいずれもHeavisideやHeavisideの演算子法をラプラス変換とその逆変換(Bromwich積分）に対比させることによって皮肉にも演算子法の正しさを裏付けたBromwichと同時代に生きていた。Ramanujanについては最近多くのエピソードが満載の伝記小説が出版されている。日本の数学者の藤原氏の著書『天才の栄光と挫折―数学者列伝』にも登場する。個人的にはNHKの番組でその主題に基づくシリーズ講話が印象に残る。とにかく身近なテーマがなんでも公式が思いついてしまう魔術士のような天才だったらしい。近年まで彼が残した公式の証明が試みられていたらしい。それだけに連分数は生きた数学なのである。

話をもとにもどそう。有理型関数の連分数展開を具体的にどうやるのか考える必要がある。公式集とかには連分数がどう表されるかは書いてあるが、どう分解するかは具体的な方法は書いていない。それだけに謎が多い。

数学的には複素関数は零点と極によって特徴付けられるので、それがどのような形の式で表現されても同じなので部分分数展開も連分数展開も重要ではない。Riemannの時代にはまだ関数を式で表現することに意義を見いだしていた学派もあったが、それは式が零点と極を定めているのか、零点と極が式を決定付けているのかの違いでしかない。数学的にはどっちでも良い話だが、物理や工学では重要な意味を持つ。零点と極はリアクタンス回路網の仕様を決定するが、部分分数展開と連分数展開とで同じ回路網を実現するのに構成が異なるという点である。周波数や位相特性はどちらも同じであるにもかかわらずである。同じことが物理学にも言えて、質量や重力が空間を歪ませているのか、空間の歪みそのものが質量や重力を創り出しているのか、数学的にはどちらも同値だが、物理的には意味が異なる。式の表し方によって物理的に異なる構成をとるのであればこれまた悩ましい問題である。

そんなこんなで連分数展開を考えている間に毎朝目の前の画面にいきなり公式が表示される夢で目が覚めるまでになってしまった。残念ながら夢の中ではスクリーンショットを取る暇はなかったので公式は憶えていない。ここ数日体調が悪くて寝込んでいた時も、胃腸の調子が悪くて意識混濁に陥っても頭の中では自分の体を一生懸命連分数展開しようとしていたのは内緒だ。

さてそろそろ連分数展開を先に進めないといかん。

連分数(continued fraction)も分数と同様に古くオイラー(Euler)やルジャンドル(Legendre)から研究され、多項式に関しても連分多項式(continuants)など数論にいくつかの重要な成果を残している。数論と言えば数学の女王と呼んだガウス(Gauss)も登場する。複素連分数に関してはフルビッツ(Hurwiz)や連分数解析理論の父と呼ばれるスチルチェス(Stieltjes)の名前が登場する。Hurwizは制御理論での安定性判定でも登場するので工学とのつながりは強い。StieltjesはRiemann-Stieltjes積分やLebesgue–Stieltjes積分の方が有名である。これらをまとめただけで一冊の本が出来るぐらいなのと、ほとんどは古典的な数論の範疇に留まっているため、目的とする多項式の連分数表現を数学的対象として扱うという試みは未踏の領域にあることだけがわかる。

こうした理由から古い回路網理論の本では２端子回路についてFosterやCauerの例を扱っているが連分数展開に及んでは具体的な方法は省略されているか、あってもEuclidの互除法に従ってヒューリスティックな多項式の除算で剰余式を割り出していくという手順が示されているのが精一杯である。もっと見通しの良いアルゴリズムは無いのかというと今のところ平易なものは存在しないと言ったほうが正しいのかもしれない。

近年に至ってはEuclidの互除法も連分数も学校では教えないことになっているので、自動的に連分数展開を伴うCauer展開を含む２端子回路そのものを教えないことになってしまっている。酷い本になると２端子回路はあるがFoster展開のみで終わっていて、Cauer展開は見事にスルーされているというものがあった。これなら２端子回路はやらないほうがまだましである。

フィルタ理論にも２端子素子のラダー接続で構成された回路をCauerに敬意を表してCauerフィルタと呼ぶことが古い本では多かったが、最近ではCauerの業績が連分数展開というやっかいなものを伴うので講師から嫌われているのか、Cauerが先駆的な研究を行った楕円(Elliptic)フィルタもかつては敬意を表してCauerフィルタと呼ばれていた。現在はその元になっている関数の多項式近似理論の中のチェビシェフ近似多項式で知られるロシアの数学者チェビシェフ(Chebychev、Chebyshov、Tchebycheff、Tschebyscheffとか色々に転記されているが同一人物である）の名で呼ばれるようになってきている。今日アナログ回路設計者の多くがチェビシェフフィルタを考案したのはチェビシェフだというまったく誤った認識を持つに至っている。Cauerの名前は歴史から葬りさられようとしているのである。ナチスドイツの暗い時代を後生に伝えるのは良くないからだろうか。ちょっと残念である。チェビシェフ近似多項式を連分数展開すると切れ味の良い特性のフィルター回路が得られるのを発見したのはCauerなのである。フィルタ理論の本にもラダー構成(Cauer展開)のことをCauerトポロジーと書いてあるもののCauerの名前はそれしか出てこなかったりする。読者に質問されたら渋々答えるしかないのだろう。知って居る者にとってはCauerの名前を永遠に葬り去るのは忍びないに違いない。読者がCauerの事を詳しく知ろうとしてももうどこにも書いて無い、誰も知らないという時代がやってくるのはそう遠くはない気がする。みんな連分数が悪いのかもしれない（ちがう）。

ということで連分数は数学的にもやっかいな代物で、数論でもEulerが扱ってしまったから触れないわけにはいかないけど、連分数をまったく知らなくても数論は体系的に理解可能というのが現実だ。連分数は未踏な領域につながっているので、深入りすると他が手につかなくなるので前途ある学生には教えない方が良いのかもしれない。そう考えることにしよう。

というわけで長くなったが、代数学的に多項式の連分数展開（主に分子が常に1になる正則連分数展開）のいくつかのバリエーションを見通しの良い単一のアルゴリズムで扱う個人的な試みは一端は諦めざるを得ない。数学的な準備が全然足らないということを思い知ったからである。代数学の古本はいくつも買ってあるが、チンプンかんぷんで理解不能である。なんとなく出来そうな予想はあるが短期間に構成できそうなものではないので、古い回路網理論の本にあるようにヒューリスティックな多項式の割り算でお茶を濁すことにしよう。いつかはこの納得の行かない点を納得の行くアルゴリズムで見通しを良くすることは読者の課題としよう（振ってどうする）。

そうすると後に学ぶフィルタ理論で埋めきれない大きな溝というか深い谷間が残ってしまう。いきなりラダー展開のフィルタ回路構成ばかりが登場するのである。それについてはその前に学ぶ２端子対回路が任意の２端子素子の結合で構成されるということを知ればフィルタ回路も２端子対回路でラダー構成も自明という理屈でごまかせるかもしれないが納得が行かない読者は少なからず居るだろう。誰が最初にラダー構成を思いついたのか、誰が最初に実用化したのか。そういう意味では思いついたのはCauerだが実用化したのはCauerではないので忘れられた存在になりつつあるのは致し方がないかもしれない。実務でのフィルタ回路は古くはAT&Tのベル研究所で多くの成果が成し遂げられているのでそちらに敬意を表するというのが当然かもしれない。Cauerは自分の特許をベル研にも売り込みに行っていてベル研の研究者も彼の存在を知ってはいたが、第二次世界大戦前にCauerは祖国ドイツに帰国したため米国の研究者は彼のことを後生に語り継げなかったに違いない。フィルタ回路理論から欠落してしまったCauerの理論は大きな深い谷間として残ることになる。なのでフィルタ回路の設計をしようとすると連分数展開でこの深い谷間を絶壁から覗き見することになる。

これまでは一般的な有理型関数としてのリアクタンス関数を前提にしてきたが先の駆動点インピーダンスの式の逆数であるアドミッタンス式として連分数展開しようとすると、分母の次数が分子の次数よりも1大きいため商は無く剰余項だけとなる。

Z(s)=\frac{1}{Y_2+\frac{1}{Z_3+\frac{1}{Y_4+\frac{1}{Z_5+...}}}}

従ってこれに対応する実際の回路構成は



ということになる。これもCauer展開である。。つまり商に対応する項が0なのでZ1項が存在しないか短絡された形になる。

ここまでで連分数展開されたインピーダンスやアドミッタンス項がそれぞれどのような受動素子で構成されるのかは触れていなかったが、実際に回路合成する際には先に問題提起したようにインダクタンスなのかキャパシタンスなのかによって回路は２つの異なる構成を取ることになる。

以下のように直列に接続されたインピーダンスがインダクタンスとして合成されたものを第一Cauer形と呼ぶ。



それに対してキャパシタンスとして合成したものを第二Cauer型と呼ぶ。



それぞれの形はω=0とω=∞に零点もしくは極のいずれかを持つかによって連分数展開の最初の項と最後の項が異なり、４つのケースが存在する。



ここでは結果だけをまとめて表すことにする。

第一Cauer形の場合

\begin{array}Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\ 2 & zero & zero & C & L\\ 3 & pole & zero & C & C\\ 4 & zero & pole & L & L\end{array}

第二Cauer形の場合

\begin{array}Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\ 2 & zero & zero & C & L\\ 3 & pole & zero & C & C\\ 4 & zero & pole & L & L\end{array}

ということになる。

一般的な回路網理論で扱われているのはここまでであるが、実際に電気回路設計に興味のある読者なら実際に設計してみたくなるかもしれない。その場合に以下の迷いが出てくる。

Foster展開とCauer展開のどちらが良いのか？　それぞれの第一形と第二形とどちらが良いのか？

またどの回路構成にするか決めたものの実際に設計しようとすると仕様をちょっと変更する度にすべての計算をやり直さないといけなという煩雑なことになる。これを緩和するのために正規化した角周波数を用いて計算結果を表にしておけば、周波数が並行移動した場合でも設計計算は最小限ですむ方法が昔から用いられてきたのでそれについてもちょっと学んでおくことにしよう。

はじめにω=0とω=∞とω=ω2に零点、ω1とω3に極を持つリアクタンス関数を考えてみよう。

Z(s)=\frac{s(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)} \\ 0 < \omega_1 < \omega_2 < \omega_3 < \infty

分子の次数が分母の次数よりも1少ないのでこれは以下の様に部分分数展開することができる。

\begin{eqnarray}&=&\frac{K_1 s}{(s^2+{\omega_1}^2)}+\frac{K_2 s}{(s^2+{\omega_3}^2)} \\ &=&\frac{1}{(\frac{1}{K_1}s+\frac{1}{\frac{K_1}{{\omega_1}^2}s})}+\frac{1}{(\frac{1}{K_2}s+\frac{1}{\frac{K_2}{{\omega_3}^2}s})} \\ &=&\frac{1}{(C_1 s+\frac{1}{L_1 s})}+\frac{1}{(C_2 s+\frac{1}{L_2 s})} \\ K_1 &=&\left.\frac{(s^2+{\omega_1}^2)}{s}(Z(s)-\frac{K_2 s}{(s^2+{\omega_3}^2)})\right|_{s^2=-{\omega_1}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_1}^2)}}{\cancel{s}}\frac{\cancel{s}(s^2+{\omega_2}^2)}{\cancel{(s^2+{\omega_1}^2)}(s^2+{\omega_3}^2)}-\frac{(s^2+{\omega_1}^2)}{\cancel{s}}\frac{K_2 \cancel{s}}{(s^2+{\omega_3}^2)}\right|_{s^2=-{\omega_1}^2} \\ &=&\frac{{\omega_2}^2-{\omega_1}^2}{{\omega_3}^2-{\omega_1}^2} \\ K_2 &=&\left.\frac{(s^2+{\omega_3}^2)}{s}(Z(s)-\frac{K_1 s}{(s^2+{\omega_1}^2)})\right|_{s^2=-{\omega_3}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_3}^2)}}{\cancel{s}}\frac{\cancel{s}(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)\cancel{(s^2+{\omega_3}^2)}}-\frac{(s^2+{\omega_3}^2)}{\cancel{s}}\frac{K_1 \cancel{s}}{(s^2+{\omega_1}^2)}\right|_{s^2=-{\omega_3}^2} \\ &=&\frac{{\omega_3}^2-{\omega_2}^2}{{\omega_3}^2-{\omega_1}^2} \\ C_1 &=&\frac{1}{K_1} \\ L_1 &=&\frac{K_1}{{\omega_1}^2} \\ C_2 &=&\frac{1}{K_2} \\ L_2 &=&\frac{K_2}{{\omega_3}^2}\end{eqnarray}

これを第一Forster形で



ということになる。

零点と極をとる角周波数をクリチカル周波数と呼び、そのうちω=0とω=∞は外部クリチカル周波数、それ以外を内部クリチカル周波数と呼ぶことにする。この場合、回路を構成するのに必要な素子数は内部クリチカル周波数（ω1,ω2,ω3)の数より常に１多いことが判る。また素子の定数が内部クリチカル周波数のみに依存することも重要な発見である。

同じリアクタンス関数の逆数はアドミッタンス関数となり分子の次数が分母の次数より1大きくなるため部分分数展開すると商として一次式が切り出されることになる。

\begin{eqnarray}Y(s)&=&\frac{1}{Z(s)}=\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s(s^2+{\omega_2}^2)} \\ &=&\frac{K_0}{s}+\frac{K_1 s}{(s^2+{\omega_2}^2)}+K_\infty s \\ &=&\frac{K_0}{s}+\frac{1}{(\frac{1}{K_1}s+\frac{1}{\frac{K_1}{{\omega_2}^2}s})}+K_\infty s \\ &=&\frac{1}{L_0 s}+\frac{1}{(L_1 s+\frac{1}{C_1 s})}+C_\infty s \\ K_0 &=&\left.s (Y(s)-\frac{K_1 s}{(s^2+{\omega_2}^2)}-K_\infty s)\right|_{s=0} \\ &=&\left.\cancel{s}\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{\cancel{s}(s^2+{\omega_2}^2)}-\frac{K_1 s^2}{(s^2+{\omega_2}^2)}- K_\infty s^2\right|_{s=0} \\ &=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2} \\ K_1 &=&\left.\frac{(s^2+{\omega_2}^2)}{s} (Y(s)-\frac{K_0}{s}-K_\infty s)\right|_{s^2=-{\omega_2}^2} \\ &=&\left.\frac{\cancel{(s^2+{\omega_2}^2)}(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s^2\cancel{(s^2+{\omega_2}^2)}}-\frac{(s^2+{\omega_2}^2)K_0}{s^2}-\frac{(s^2+{\omega_2}^2)}{\cancel{s}}K_\infty \cancel{s}\right|_{s^2=-{\omega_2}^2} \\ &=&\frac{({\omega_2}^2-{\omega_1}^2)({\omega_3}^2-{\omega_2}^2)}{{\omega_2}^2} \\ K_\infty &=&\left.\frac{Y(s)-\frac{K_0}{s}-\frac{K_1 s}{(s^2+{\omega_2}^2)}}{s}\right|_{s^2=\infty} \\ &=&\left.\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s^2(s^2+{\omega_2}^2)}-\frac{K_0}{s^2}-\frac{K_1}{(s^2+{\omega_2}^2)}\right|_{s^2=\infty} \\ &=&\left.\frac{(1+\frac{{\omega_1}^2}{s^2})(1+\frac{{\omega_3}^2}{s^2})}{(1+\frac{{\omega_2}^2}{s^2})}\right|_{s^2=\infty}=1 \\ L_0 &=&\frac{1}{K_0} \\ L_1 &=&\frac{1}{K_1} \\ C_1 &=&\frac{K_1}{{\omega_2}^2} \\ C_\infty &=&K_\infty\end{eqnarray}

これを第二Foster展開で



ということになる。

次ぎに同じリアクタンス関数をCauer展開（連分数展開）をしてみることにしよう。

連分数展開するには先のリアクタンス関数の分子と分母をそれぞれ多項式に展開してEuclidの互除法を使ってヒューリスティックに式変形を行う必要がある。ずばり結論だけが得られる方法があればよいのだが今日の数学者の範疇外なので未踏のまま残されている。

\begin{eqnarray}Z(s)&=&\frac{s(s^2+{\omega_2}^2)}{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)} \\ &=&\frac{s^3+{\omega_2}^2 s}{s^4+({\omega_1}^2+{\omega_3}^2) s^2+{\omega_1}^2{\omega_3}^2}\end{eqnarray}

分子の次数が分母の次数よりも１小さいので商が得られないため上の式そのものが剰余の式となる。連分数展開では剰余の逆数から商と剰余を切り出し、割り切れるか分子の式が定数になるまで繰り返すことになる。やってみると、

\begin{array}{rrrrrrl}s^3+{\omega_2}^2 s ) & s^4 & + & ({\omega_1}^2+{\omega_3}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & ( s \\ & s^4 & + & {\omega_2}^2 s^2 & & & \\ \hline & & & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & \end{array}

従って

Z(s)=\frac{1}{s+\frac{({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2}{s^3+{\omega_2}^2 s}}

ということになる。分母の式にまだ残っている剰余を更に連分数展開すると

\begin{array}{rrrrrrl}({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2 ) & s^3 & + & {\omega_2}^2 s & & & ( \frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s \\ & s^3 & + & \frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} s & & & \\ \hline & & & ({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s & & & \end{array}

従って

Z(s)=\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s}{({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2+{\omega_1}^2{\omega_3}^2}}}

ということになる。まだ有理型多項式の剰余が残っているので更に連分数展開すると

\begin{array}{rrrrrrl}({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s ) & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & + & {\omega_1}^2{\omega_3}^2 & & & ( \frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s \\ & ({\omega_1}^2+{\omega_3}^2-{\omega_2}^2) s^2 & & & & & \\ \hline & & & {\omega_1}^2{\omega_3}^2 & & & \end{array}

従って

\begin{eqnarray}Z(s)&=&\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s+\frac{{\omega_1}^2{\omega_3}^2}{({\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}) s}}}} \\ &=&\frac{1}{s+\frac{1}{\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}s+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}s+\frac{1}{\frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2}s}}}} \\ &=&\frac{1}{C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s+\frac{1}{L_5 s}}}} \\ C_2 &=& 1 \\ L_3 &=& \frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} \\ C_4 &=& \frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}} \\ L_5 &=& \frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2}\end{eqnarray}

ということになる。

これは第一Cauer形



最後の第二Cauer形への展開だが、第二Foster形と同様にリアクタンス関数の逆数であるアドミッタンス関数として扱うのだが、予めsの逆数pでリアクタンス関数の式を書き直すと連分数展開が第一Cauer形と同じ要領でできることにようやく気づいた。これが長い間躓いていた原因だったのだが、これが変換群を成すという意味なのか。

\begin{eqnarray}Y(s) &=&\frac{1}{Z(s)} \\ &=&\frac{(s^2+{\omega_1}^2)(s^2+{\omega_3}^2)}{s(s^2+{\omega_2}^2)} \\ &=&\frac{s^4+({\omega_1}^2+{\omega_3}^2) s^2+{\omega_1}^2{\omega_3}^2}{s^3+{\omega_2}^2 s} \\ &=&\frac{1+({\omega_1}^2+{\omega_3}^2) s^{-2}+{\omega_1}^2{\omega_3}^2 s^{-4}}{s^{-1}+{\omega_2}^2 s^{-3}} \\ &=&\frac{{\omega_1}^2{\omega_3}^2 s^{-4}+({\omega_1}^2+{\omega_3}^2) s^{-2}+1}{{\omega_2}^2 s^{-3}+s^{-1}} \\ &=&\frac{{\omega_1}^2{\omega_3}^2 p^{4}+({\omega_1}^2+{\omega_3}^2) p^{2}+1}{{\omega_2}^2 p^{3}+p} \\ p &=& s^{-1}\end{eqnarray}

こうしておけば第一Cauer形と同様に連分数展開するだけである

\begin{array}{rrrrrrl}{\omega_2}^2 p^{3}+p ) & {\omega_1}^2{\omega_3}^2 p^{4} & + & ({\omega_1}^2+{\omega_3}^2) p^{2} & + & 1 & ( \frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p \\ & {\omega_1}^2{\omega_3}^2 p^{4} & + & \frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p^{2} & & & \\ \hline & & & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & + & 1 & \end{array}

従って

\begin{eqnarray}Y(s)=\frac{1}{Z(s)}&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1}{{\omega_2}^2 p^{3}+p}\end{eqnarray}

剰余項を更に同様に連分数展開すると

\begin{array}{rrrrrrl}({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1 ) & {\omega_2}^2 p^{3} & + & p & & & ( \frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p \\ & {\omega_2}^2 p^{3} & + & \frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p & & & \\ \hline & & & (1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p & & & \end{array}

従って

\begin{eqnarray}Y(s)&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p+\frac{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}{({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2}+1}}\end{eqnarray}

まだ剰余項が有理型多項式なので更に連分数展開すると

\begin{array}{rrrrrrl}(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p ) & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & + & 1 & & & ( \frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p \\ & ({\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}) p^{2} & & & & & \\ \hline & & & 1 & & & \end{array}

従って最終的には

\begin{eqnarray}Y(s)&=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}p+\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}p+\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p+\frac{1}{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}}} \\ &=&\frac{1}{\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2}}p+\frac{1}{\frac{1}{\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2}}p+\frac{1}{\frac{1}{\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}p+\frac{1}{(1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}})p}}} \\ &=&\frac{1}{L_1 s}+\frac{1}{\frac{1}{C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}} \\ L_1 &=&\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2} \\ C_2 &=&\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2} \\ L_3 &=&\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}} \\ C_4 &=&\frac{1}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}} \end{eqnarray}

これは第二Cauer形



ということになる。

ふう、計算が想像以上に面倒くさい。何度も間違いを犯したが、検証するにも複雑すぎる。実際にω1,ω2,ω3に適当に値を与えてグラフをプロットしてみることで確認してみよう。

ω1=1000*2π,ω2=1500*2π,ω3=2000*2πとして第一Foster形、第二Foster形、第一Cauer形、第二Cauer形のそれぞれの式に代入して素子の定数を求め回路シミュレーターで周波数特性をシミュレーションしてみよう。

第一Foster形：

\begin{eqnarray}K_1 &=&\frac{{\omega_2}^2-{\omega_1}^2}{{\omega_3}^2-{\omega_1}^2} = \frac{{1500}^2-{1000}^2}{{2000}^2-{1000}^2} = \frac{5}{12}\\ K_2 &=&\frac{{\omega_3}^2-{\omega_2}^2}{{\omega_3}^2-{\omega_1}^2} = \frac{{2000}^2-{1500}^2}{{2000}^2-{1000}^2} = \frac{7}{12}\\ C_1 &=&\frac{1}{K_1} = \frac{12}{5} = 2.4 [F]\\ L_1 &=&\frac{K_1}{{\omega_1}^2} =\frac{\frac{5}{12}}{(1000\,2\pi)^2} = \frac{1}{9600000\,{\pi }^{2}} = 1.055\,10^{-8} [H]\\ C_2 &=&\frac{1}{K_2} = \frac{1}{\frac{7}{12}} = \frac{12}{7} = 1.714 [F]\\ L_2 &=&\frac{K_2}{{\omega_3}^2} = \frac{\frac{7}{12}}{(2000\,2\pi)^2} = \frac{7}{192000000\,{\pi }^{2}} = 3.694\,10^{-9} [H]\end{eqnarray}

このリアクタンス関数の式では便宜上スケールファクタ(H)を1固定としているが実際にはスケールファクタを変えることによって素子の定数はより入手可能な範囲にすることができる。

とりあえずこの定数で回路を組んで周波数特性を見てみると



1000Hz(ω1)と2000Hz(ω2)にピークが、1500Hz(ω2)にボトムが現れており意図したとおりの特性が出ていることが確認できた。

同様に第二Foster型に関しても

\begin{eqnarray}K_0 &=&\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2} = \frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1500\,2\pi)^2}=\frac{64000000\,{\pi }^{2}}{9}\\ K_1 &=&\frac{({\omega_2}^2-{\omega_1}^2)({\omega_3}^2-{\omega_2}^2)}{{\omega_2}^2} \\ &=&\frac{((1500\,2\pi)^2-(1000\,2\pi)^2)((2000\,2\pi)^2-(1500\,2\pi)^2)}{(1500\,2\pi)^2} =\frac{35000000\,\pi^2}{9}\\ K_\infty &=&1 \\ L_0 &=&\frac{1}{K_0} =\frac{9}{64000000\,{\pi }^{2}}=1.425\,{10}^{-8} [H]\\ L_1 &=&\frac{1}{K_1}=\frac{9}{35000000\,\pi^2}= 2.605\,10^{-8} [H]\\ C_1 &=&\frac{K_1}{{\omega_2}^2}=\frac{\frac{35000000\,\pi^2}{9}}{(1500\,2\pi)^2}= \frac{35}{81}=0.432 [F]\\ C_\infty &=&K_\infty=1 [F]\end{eqnarray}



こちらも1000Hz,1500Hz,2000Hzにそれぞれピークが現れているので合っている。

次ぎは第一Cauer形

C_2 &=&1[F] \\ L_3 &=&\frac{1}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2} = \frac{1}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2} = \frac{1}{11000000\,{\pi }^{2}} = 9.211\,{10}^{-9}[H]\\ C_4 &=&\frac{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}} = \frac{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}{(1500\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}} = \frac{121}{35} = 3.457[F] \\ L_5 &=&\frac{{\omega_2}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_1}^2+{\omega_3}^2-{\omega_2}^2}}{{\omega_1}^2{\omega_3}^2} = \frac{(1500\,2\pi)^2-\frac{(1000\,2\pi)^2(2000\,2\pi)^2}{(1000\,2\pi)^2+(2000\,2\pi)^2-(1500\,2\pi)^2}}{(1000\,2\pi)^2(2000\,2\pi)^2} = \frac{7}{140800000\,{\pi }^{2}} = 5.037\,{10}^{-9}[H]\end{eqnarray}



これもどうやら合っているようだ。

最後に第二Cauer形





こちらも同じ特性を持っていることが確認できた。

もともとのリアクタンス関数の式がスケールファクタ(H)を1としているので現実的ではない大容量のキャパシタ定数になっているが、H=10^6とするとキャパシタンス定数はHで割り、インダクタンスはHを乗じれば良いので以下の様に現実的な定数の素子で同じ周波数特性(ただしインピーダンスはH倍になる）の回路が得られる。



これらのことから仕様を満たす回路合成の可能性が見いだされたことは当時大きな驚きであったことは想像に難くない。それまでは試行錯誤で定数を見いだしていたのだから。

受動素子のみからなる回路が今日あまり熱心に教えないのは以下の理由によるものであることはすぐに気づく

・市販されている標準数列に基づいた定数の受動素子がほとんど利用できない
・現実のインダクタンスは定数が大きくなればなるほど（巻き数が多いほど）漏洩キャパシタンスが多くなる
・大容量のキャパシタンスやインダクタンスは容積が大きくかさばる
・インダクタンスは隣接する他のインダクタンスと意図しない相互誘導を受ける
・低インピーダンスな回路にしようとすると定数が更に非現実的となる（キャパシタンスはF単位と巨大にインダクタンスはnH単位と極端に微少になってしまう）
・直流を素子する必要のある回路では周辺回路の直流阻止キャパシタ（ブロッキング・キャパシタ）を考慮して回路構成を決定する必要がある
・現実の回路では２端子素子を複数組み合わせた入力端子と出力端子からなる２端子対回路を設計することが不可欠
・理論を理解するのに複素解析の数学的前提知識が不可欠

おそらく一端子対回路が学校で教えられなくなった背景にはこれらの理由が考えられる。中でも一番の理由は最後の複素解析の知識が必要であることが、高校卒者に電気回路理論を教えるのに大いなる妨げになるということがあるに違いない。日本の電気学会では唯一複素解析の知識が必要となる一端子対回路は早々と割愛してしまっている。ラプラス変換も複素積分の概念が理解には必要だが、それを知らなくても演算子法と同様に数式処理のテクニックとして詰め込むことは可能なので残っている。今日ではLとCだけからなる回路は高級なオーディオスピーカーユニット内部のネットワーク回路ぐらいだろう。

話をもとにもどそう。最後にフィルタ設計で当たり前のように登場する正規化(Normalized)周波数について触れて終わりにしよう。それ以外にも周波数領域以外に位相特性はどうなるのかという疑問が湧くがそれは比較的自明なので読者の課題としよう。

正規化周波数は特定の基準周波数（クリチカル周波数、アナログフィルタのカットオフ周波数や中心周波数、デジタルフィルタのナイキスト周波数など）を1として任意の周波数をそれとの比率で表したものである。これによって低周波から高周波まで極めて広範囲なレンジを持つ実際の周波数を用いることなく計算を容易にする。

正規化周波数を用いて前述のFoster展開やCauer展開で定数を求めると正規化されたインダクタンスやキャパシタンスの値が得られることになる。実際の所望の周波数での定数を求めるにはこれらの正規化インダクタンスやキャパシタンスを所望の周波数で割れば済む。

このように正規化周波数を使用して一度正規化された素子の定数を求めてしまえば、所望の周波数に基準周波数からシフトした場合の実際の定数は計算尺一つ（今は電卓か）で求めることができて設計がし易いということになる。

任意の正規化（角）周波数(ω')と任意の角周波数(ω)と基準角周波数(ω0)との間では以下の関係が成り立つ

\begin{eqnarray}\omega'&=&\frac{\omega}{\omega_0} \\ \omega&=&\omega'\omega_0\end{eqnarray}

これをs=jωとした駆動点インピーダンス関数の式に代入すると

\begin{eqnarray}Z(\omega)&=& -j H \frac{\left(-{\omega}^2+{\omega_{1}}^2\right)\left(-{\omega}^2+{\omega_{3}}^2\right)...\left(-{\omega}^2+{\omega_{2n-1}}^2\right)}{\omega \left(-{\omega}^2+{\omega_{2}}^2\right)\left(-{\omega}^2+{\omega_{4}}^2\right)...\left(^{\omega}^2+{\omega_{2n-2}}^2\right)} \\ Z(\omega')&=& -j H \frac{\left(-(\omega'\omega_0)^2+(\omega_{1}'\omega_0)^2\right)\left(-(\omega'\omega_0)^2+(\omega_{3}'\omega_0)^2\right)...\left(-(\omega'\omega_0)^2+(\omega_{2n-1}'\omega_0)^2\right)}{\omega'\omega_0 \left(-(\omega'\omega_0)^2+(\omega_{2}'\omega_0)^2\right)\left(-(\omega'\omega_0)^2+(\omega_{4}'\omega_0)^2\right)...\left(-(\omega'\omega_0)^2+(\omega_{2n-2}'\omega_0)^2\right)} \\ &=& -j H \frac{{\omega_0}^{2n}\left(-\omega'^2+\omega_{1}'^2\right)\left(-\omega'^2+\omega_{3}'^2\right)...\left(-\omega'^2+\omega_{2n-1}'^2\right)}{{\omega_0}^{2n-1} \omega' \left(-\omega'^2+\omega_{2}'^2\right)\left(-\omega'^2+\omega_{4}'^2\right)...\left(-\omega'^2+\omega_{2n-2}'^2\right)} \\ &=& -j H \frac{\omega_0 \left(-\omega'^2+\omega_{1}'^2\right)\left(-\omega'^2+\omega_{3}'^2\right)...\left(-\omega'^2+\omega_{2n-1}'^2\right)}{ \omega' \left(-\omega'^2+\omega_{2}'^2\right)\left(-\omega'^2+\omega_{4}'^2\right)...\left(-\omega'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}

ということになる。今度は正規化複素周波数

s'=j\omega'

で置き換えると駆動点インピーダンスの式は

ω=0とω=∞に極を持つケースで

\begin{eqnarray}Z(s')&=& H \omega_0 \frac{\left(s'^2+\omega_{1}'^2\right)\left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-1}'^2\right)}{ s' \left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}

ということになる。

同様にω=0に零点、ω=∞に極を持つケースでは

\begin{eqnarray}Z(s')&=& H \omega_0 \frac{s' \left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-1}'^2\right)}{\left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)} \end{eqnarray}

ということになる。

同様にω=∞に零点を持つ場合には分子の次数が分母の次数より1少なくなるのでそれぞれ

ω=0に極、ω=∞に零点を持つケース

\begin{eqnarray}Z(s')&=& \frac{H}{\omega_0} \frac{\left(s'^2+\omega_{1}'^2\right)\left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-3}'^2\right)}{ s' \left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}

ω=0とω=∞に零点を持つケース

\begin{eqnarray}Z(s')&=& \frac{H}{\omega_0} \frac{s' \left(s'^2+\omega_{3}'^2\right)...\left(s'^2+\omega_{2n-3}'^2\right)}{\left(s'^2+\omega_{2}'^2\right)\left(s'^2+\omega_{4}'^2\right)...\left(s'^2+\omega_{2n-2}'^2\right)}\end{eqnarray}

ということになる。

実際に前出の第二Cauer展開を正規化周波数を用いて展開して整理みると

\begin{eqnarray}Y(s')&=&\frac{1}{L_1' s'}+\frac{1}{\frac{1}{C_2' s'}+\frac{1}{\frac{1}{L_3' s'}+C_4' s'}} \\ L_1' &=&\frac{1}{\omega_0}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} = \omega_0 L_1 \\ L_1 &=& \frac{L_1'}{\omega_0} \\ C_2' &=&\omega_0\frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} = \omega_0 C_2 \\ C_2 &=& \frac{C_2'}{\omega_0}\\ L_3' &=&\frac{1}{\omega_0}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}} = \omega_0 L_3 \\ L_3 &=& \frac{L_3'}{\omega_0} \\ C_4' &=&\omega_0 \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}} = \omega_0 C_4 \\ C_4 &=& \frac{C_4'}{\omega_0}\end{eqnarray}

ということになる。

また元の定数の式にω=ω'ω0を代入しても同じ結果が得られる。

\begin{eqnarray}L_1 &=&\frac{{\omega_2}^2}{{\omega_1}^2{\omega_3}^2} = \frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2} = \frac{1}{\omega_0^2}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} = \frac{L_1'}{\omega_0} \\ L_1' &=&\frac{1}{\omega_0}\frac{{\omega_2'}^2}{{\omega_1'}^2{\omega_3'}^2} \\ C_2 &=&\frac{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}{{\omega_2}^2} = \frac{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}{(\omega_2'\omega_0)^2} = \frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} = \frac{C_2'}{\omega_0} \\ C_2' &=& \omega_0 \frac{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}{{\omega_2'}^2} \\ L_3 &=&\frac{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}} = \frac{1-\frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}} = \frac{1}{\omega_0^2}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}} = \frac{L_3'}{\omega_0} \\ L_3' &=& \frac{1}{\omega_0}\frac{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}\\ C_4 &=&\frac{1}{1-\frac{{\omega_2}^2}{{\omega_1}^2+{\omega_3}^2-\frac{{\omega_1}^2{\omega_3}^2}{{\omega_2}^2}}} = \frac{1}{1-\frac{(\omega_2'\omega_0)^2}{(\omega_1'\omega_0)^2+(\omega_3'\omega_0)^2-\frac{(\omega_1'\omega_0)^2(\omega_3'\omega_0)^2}{(\omega_2'\omega_0)^2}}} = \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}} = \frac{C_4'}{\omega_0} \\ C_4' &=& \omega_0 \frac{1}{1-\frac{{\omega_2'}^2}{{\omega_1'}^2+{\omega_3'}^2-\frac{{\omega_1'}^2{\omega_3'}^2}{{\omega_2'}^2}}}\end{eqnarray}


従って正規化周波数で計算した値を所望の周波数で割れば所望のクリチカル周波数に特性をシフトした回路が得られることになる。実際にやってみると

ω0=ω2=1500*2π(rad/sec) として正規化された素子定数を求めると



正規化された駆動点インピーダンス関数の絶対値をプロットしてみると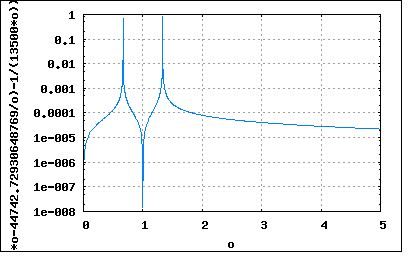



確かにω2'=1(rad/sec)になっているのがわかる。

今度はω0=455000*2*πとして中心周波数を455kHzにシフトした場合の定数を計算すると



これらの定数に変えて回路シミュレータで周波数特性を測定すると



見事に中心周波数ω0=ω2=455kHzにシフトしている。ω1とω3はそれぞれω2との元の比率を保っていることもわかる。

これらの理論が考案された時代にはまだ電子計算機は利用できなかったので、もっぱら設計計算の現場では数値計算は計算尺が用いられていた。設計技術者はそれぞれ胸ポケットに必ず計算尺を忍び込ませていたものである。
フラット表示 前のトピック | 次のトピック

題名 投稿者 日時
   1端子対回路 webadm 2009-10-15 7:06
     複素角周波数 webadm 2009-10-15 19:22
     インピーダンス関数 webadm 2009-10-15 21:47
     正実関数(Positive Real Function) webadm 2009-10-16 1:11
     リアクタンス関数 webadm 2009-10-22 7:47
     Foster展開（部分分数展開） webadm 2009-11-11 19:00
   » Cauer展開（連分数展開） webadm 2009-11-12 1:04
       Re: Cauer展開（連分数展開） webadm 2009-12-20 2:36
     RL一端子対回路 webadm 2009-12-2 4:14
     RC一端子対回路 webadm 2009-12-24 19:18
     逆回路(Inverse Network) webadm 2009-12-25 18:57
     定抵抗回路(constant resistance network) webadm 2009-12-25 21:21

投稿するにはまず登録を
 
ページ変換(Google Translation)
EQPlayers
Allakhazam
EQresource VoA Home
Googleish(EN)
Googlean(KO)
Googlchinese(ZH-CN)
Googltwinese(ZH-TW)
Googlussian(RU)
Googlench(FR)
Googlerman(DE)
Googlabic(AR)
Googlindi(HI)
Googluguese(PT)
Googlutch(NL)
Googltarian(IT)
Googlpanish(ES)
Googlinnish(FJ)
Googlwedish(SY)
Googlatian(HR)
Googlzech(CS)
Googlgarian(BG)
Googlpolish(PL)
Googlmanian(RO)
Googlwegian(NO)
Googleek(EL)
Googldanish(DA)
サイト内検索

高度な検索