ログイン
ユーザ名:

パスワード:


パスワード紛失

新規登録
Main Menu
Tweet
Facebook
Line
:-?
フラット表示 前のトピック | 次のトピック
投稿者 スレッド
webadm
投稿日時: 2010-5-10 12:46
Webmaster
登録日: 2004-11-7
居住地:
投稿: 3086
影像パラメータ
ここでは影像インピーダンスと伝達定数から成る影像パラメータを学ぶ。

影像パラメータは戦前に米国（Otto J. Zobel、George Campbell、Sidney Darlington、M. Reedら）で体系化された古典的な影像フィルタ理論の一部である。

戦後になってトランジスタやオペアンプが登場して以来、近代的なフィルタ理論が登場し古典的な理論は隅へ追いやられた感がある。

元来は戦前に発明され需用が急拡大していった電話網の伝送路内に挿入する低損失な受動素子からのみなる等価器やフィルタの研究開発に端を発する理論である。

既にここまでで、二端子回路の縦続接続について学んだが、それで電話網に導入する受動素子フィルタを設計する上でひとつ問題が持ち上がる。

最終端子対に負荷を接続した場合に縦続接続されている各小回路の出力端子対の出力インピーダンスが、後続する小回路の入力端子対の駆動点インピーダンスと等しくないと最大電力が供給されないという問題である。最悪入力された信号がほとんど出力に出てこないことになってしまう。これではまったく役にたたない。

このことは本書を含め電気回路のほとんどの参考書に書かれていないことで、あくまで個人的な推測である。

一体何故影像インピーダンスを持ち出さなければならないのかその理由が知りたかったのであるが、考案されたのが戦前なので、もうすでに研究者も亡くなって久しいため知るよしもない。想像するしかないのである。

上記の仮説に基づいて、戦前に立ち戻って上記の問題を解決しようとすると、影像インピーダンスというアイデアの真意が理解できるわけである。

著者の記述は最初からまとめに走っているので鵜呑みにしようにも喉を通らない。

そこでもっとゆっくり考えて見ることにする。

（１）影像インピーダンス(image impedances)

著者もそうだが、影像インピーダンスの英語表記を単数のimage impedanceと書いている。日本語だと複数と単数の区別ができないのだがオリジナルは複数形である。つまり一般的に影像インピーダンスは２つあることを意味する。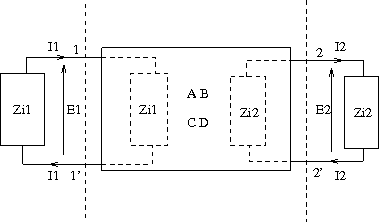



一般的（相反で非対称）な二端子対回路の２つの端子対をそれぞれZi1とZi2のインピーダンスで終端した場合に、端子対1-1'から見た駆動点インピーダンスが端子対1-1'に接続されたZi1と等しく、端子対2-2'から見た駆動点インピーダンスが端子対2-2'に接続されたZi2に等しくなるようなZi1,Zi2を影像インピーダンス(image impedances)と呼ぶ。(2010/8/21訂正）

つまり図にあるように端子対を境界線とすると境界の左右でインピーダンスが同一であるかのように見えるということを意味する。一般的に二端子対回路が非対称回路の場合、Zi1≠Zi2であるが対称回回路の場合はZi1＝Zi2となる。

著者は矢継ぎ早に伝達定数の定義に入っているが、ちょっとその前に影像インピーダンスについてもっとよく知る必要がある。

上図でZi1,Zi2がFパラメータでどのように表されるのか考えてみよう。

Zi1は

\begin{eqnarray}<br />Z_{i1}&=&\frac{E_1}{I_1}\\<br />&=&\frac{A E_2+B I_2}{C E_2+D I_2}\\<br />&=&\frac{A Z_{i2}I_2+B I_2}{C Z_{i2}I_2+D I_2}\\<br />&=&\frac{A Z_{i2}+B}{C Z_{i2}+D}<br />\end{eqnarray}

Zi2はFiパラメータを使用して求めてもよいがAとDが逆になるだけなので書き換えると

\begin{eqnarray}<br />Z_{i2}&=&\frac{E_2}{I_2}\\<br />&=&\frac{D E_1+B I_1}{C E_1+A I_1}\\<br />&=&\frac{D Z_{i1}I_1+B I_1}{C Z_{i1}I_1+A I_1}\\<br />&=&\frac{D Z_{i1}+B}{C Z_{i1}+A}<br />\end{eqnarray}

ということになる。

ここでZi1、Zi2それぞれ∞とすると終端開放時のインピーダンス(Zo1,Zo2)が、Zi1,Zi2をそれぞれ0とすると終端短絡時のインピーダンス(Zs1,Zs2)が導かれる。これは後で重要になる。

\begin{eqnarray}<br />Z_{o1}&=&\lim_{Z_{i2}\to\infty}\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\lim_{Z_{i2}\to\infty}\frac{A+\frac{B}{Z_{i2}}}{C+\frac{D}{Z_{i2}}}\\<br />&=&\frac{A}{C}<br />Z_{o2}&=&\lim_{Z_{i1}\to\infty}\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\lim_{Z_{i1}\to\infty}\frac{D+\frac{B}{Z_{i1}}}{C+\frac{A}{Z_{i1}}}\\<br />&=&\frac{D}{C}\\<br />Z_{s1}&=&\lim_{Z_{i2}\to0}\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\frac{B}{D}<br />Z_{s2}&=&\lim_{Z_{i1}\to0}\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\frac{B}{A}<br />\end{eqnarray}

ここで先のZi1,Zi2の式からそれぞれZi2,Zi1を消去すると

\begin{eqnarray}<br />Z_{i1}&=&\frac{A Z_{i2}+B}{C Z_{i2}+D}\\<br />&=&\frac{A \frac{D Z_{i1}+B}{C Z_{i1}+A}+B}{C \frac{D Z_{i1}+B}{C Z_{i1}+A}+D}\\<br />&=&\frac{\frac{A D Z_{i1}+A B+B\left(C Z_{i1}+A\right)}{\cancel{C Z_{i1}+A}}}{\frac{C D Z_{i1}+C B+D\left(C Z_{i1}+D\right)}{\cancel{C Z_{i1}+A}}}\\<br />&=&\frac{\left(A D+B C\right)Z_{i1}+2 A B}{2 C D Z_{i1}+A D+B C}\\<br />&=&\frac{\frac{A D+B C}{2 C D}Z_{i1}+\frac{A B}{C D}}{Z_{i1}+\frac{A D+B C}{2 C D}}\\<br />Z_{i1}\left(Z_{i1}+\frac{A D+B C}{2 C D}\right)&=&\frac{A D+B C}{2 C D}Z_{i1}+\frac{A B}{C D}\\<br />{Z_{i1}}^2&=&\frac{A B}{C D}=Z_{o1}Z_{s1}\\<br />Z_{i1}&=&\pm\sqrt{Z_{o1}Z_{s1}}\\<br />Z_{i2}&=&\frac{D Z_{i1}+B}{C Z_{i1}+A}\\<br />&=&\frac{D \frac{A Z_{i2}+B}{C Z_{i2}+D}+B}{C \frac{A Z_{i2}+B}{C Z_{i2}+D}+A}\\<br />&=&\frac{\frac{A D Z_{i2}+B D+B\left(C Z_{i2}+D\right)}{\cancel{C Z_{i2}+D}}}{\frac{A C Z_{i2}+B C+A\left(C Z_{i2}+D\right)}{\cancel{C Z_{i2}+D}}}\\<br />&=&\frac{\left(A D+B C\right)Z_{i2}+2 B D}{2 A C Z_{i2}+A D+B C}\\<br />&=&\frac{\frac{A D+B C}{2 A C}Z_{i2}+\frac{B D}{A C}}{Z_{i2}+\frac{A D+B C}{2 A C}}\\<br />Z_{i2}\left(Z_{i2}+\frac{A D+B C}{2 A C}\right)&=&\frac{A D+B C}{2 A C}Z_{i2}+\frac{B D}{A C}\\<br />{Z_{i2}}^2&=&\frac{B D}{A C}=Z_{o2}Z_{s2}\\<br />Z_{i2}&=&\pm\sqrt{Z_{o2}Z_{s2}}<br />\end{eqnarray}

ということになる。厳密にはZi1,Zi2に±の２つの極性があることになるが、受動回路ではインピーダンスの実数部が負になるような負性抵抗や負のインピーダンスは存在しない。能動回路や、ポテンシャル場が支配的な半導体や超電導素子のような微小な量子結晶構造を伴う分布定数回路ではどちらの極性をもとり得る。Maxwellの方程式からスカラー項を取り除いてベクトル項から成る現在知られる簡易な式に書き換えたのはHeavisideだが、自身では負の抵抗の存在の可能性を考えていたのは皮肉だ。後にHeavisideが取り除いたスカラー項は近代になってポテンシャル場の存在が確認されるに至って復活することになった。得に結晶構造内での電磁気現象を扱う必要のある半導体分野では正負両方あると考えると都合がよい。

対称回路では２つの影像インピーダンスは互いに等しく

Z_{i1}=Z_{i2}=Z_i

と単一の影像インピーダンス(Zi)で表され、また対称回路ではA=Dとなるので

\begin{eqnarray}<br />{Z_i}^2&=&{Z_{i1}}^2=\frac{\cancel{A} B}{C \cancel{D}}={Z_{i2}}^2=\frac{B \cancel{D}}{\cancel{A} C}=\frac{B}{C}=Z_{o1}Z_{s2}=Z_{s1}Z_{o2}\\<br />Z_i&=&Z_{i1}=Z_{i2}=\pm\sqrt{Z_{o1}Z_{s2}}=\pm\sqrt{Z_{s1}Z_{o2}}<br />\end{eqnarray}

ということになる。ここでもZiには正負両極性考えられるが、受動回路では正極性のみに限定される。

（２）影像伝達定数(image transfer constant)

さて残るは伝達定数。著者はいきなり結論だけ示しているがこれだけだと何が何やら。そもそも損失の無いリアクタンス回路からなる二端子対回路をインピーダンス整合させて縦続接続すれば供給される電力は最終端の負荷で消費される電力と等しくなるが（理想的なリアクタンス回路は電力を消費しない）、現実の回路はなんらかの損失を伴う（RやGが含まれる）ため回路内で電力が消費されるので出力側に供給される電力はその分目減りする。

そうした損失を伴う二端子対回路（フィルターやイコライザー）を複数縦続接続して電話網の伝送路に挿入した場合にどれだけ信号が減衰するかを予め計算する必要がある。途中に減衰分を補う増幅回路を追加する必要があるからだ。縦続接続された各二端子回路の入力と出力の電力比が計算できたとすると、全体の入力と出力の電力比は、各電力比の乗除算になる。これだと計算がやっかいなので、戦前に既にベル研究所の研究者達はその比率を対数に変換することで、乗除算ではなく加減算で全体の電力伝達比を簡単に計算できるように考えた。戦後になって常用対数に基づくdB(デジベル）が標準となったが、それ以前は理論的な自然対数に基づくNp(ネーパ）が主だった。現代的なフィルタ理論とコンピュータが登場する以前は、机上での解析や手計算が容易な最小規模の二端子対回路としてフィルタ回路を設計し、それを複数接続することによって試行錯誤的に目的に見合うフィルタを設計していたという時代的な背景がある。

その頃の考え方から説明する参考書は現代でもわずかながらある。しかし新しい入門書では影像パラメータそのものが割愛されてしまっているケースがほとんどである。特に現代的なフィルタ理論を学ぶ上では、既に二端子回路で学んだような複素有理関数で表される伝達関数として一度正規化されたフィルタを設計すれば、コンピュータプログラムを使って同一回路でスケーリングファクタを変えるだけで任意の周波数とインピーダンスのフィルタに必要な定数を割り出すことができる。これは既に二端子回路で学んだ通りである。それでも考え方としては現在でも様々な局面で登場するものなので知っておいても損はないという感じである。

手元にある参考書で最も古いと思われるものでは、1932年に初版が出版された、ドイツのK. K醇аfm醇・lerによる,「 Einf醇・rung in die theoretische Elektrotechnik」英文に題名を訳すと [Introduction to the theory of electrical engineering]の戦後復刻版(1959年版）に明快な解説を見いだすことができた。K. K醇аfm醇・lerは戦前(1931年)に同じ頃Nyquistが予想し米国で発表していた信号の再現限界周波数（Nyquist周波数と呼ばれる）を独立に発見し論文を発表していたことが戦後になって知られるにいたったことで有名である。ドイツでは現在もこの本の改訂新版が理論電気学の教科書になっているらしい。

その本の内容から学ぶべきことは現代的な表現で紹介することにしよう。

伝達定数(transfer constant)で検索すると異なる分野で同じ用語が使用されている。影像パラメータのそれは古くは影像伝搬定数もしくは影像伝達定数(image transfer constant)が呼ぶのが正しいようだ。既に科学辞書にしかまともな定義を見出すことはできない始末だ。

Sci-Tech Dictionary:
image transfer constant
(′im·ij ′tranz·fər ′k醇Bn·stənt)

(electronics) One-half the natural logarithm of the complex ratio of the steady-state apparent power entering and leaving a network terminated in its image impedance.

（電気）影像インピーダンスで終端された回路網において定常状態で流入及び流出する見掛け上の電力の複素比率を自然対数で表した値の1/2。

これの意味から考えるのがよさそうである。

最初の影像インピーダンスの図に端子対1-1'側に電源を挿入したものを考える。



ここで端子対1-1'側から回路に供給される見かけ上の電力P1は

\begin{eqnarray}<br />P_1&=&E_1 I_1\\<br />&=&E_1\frac{E_1}{Z_{i1}}\\<br />&=&\frac{{E_1}^2}{Z_{i1}}\\<br />&=&\frac{{Z_{i1}}^2{I_1}^2}{Z_{i1}}\\<br />&=&Z_{i1}{I_1}^2<br />\end{eqnarray}

と表される。一方端子対2-2'の負荷側に供給される見かけ上の電力P2は

\begin{eqnarray}<br />P_2&=&E_2 I_2\\<br />&=&E_2\frac{E_2}{Z_{i2}}\\<br />&=&\frac{{E_2}^2}{Z_{i2}}\\<br />&=&\frac{{Z_{i2}}^2{I_2}^2}{Z_{i2}}\\<br />&=&Z_{i2}{I_2}^2<br />\end{eqnarray}

と表される。

影像伝達定数は先の定義によりP1とP2の比の自然対数を1/2したものであるので

\begin{eqnarray}<br />\theta&=&\frac{1}{2}\ln\frac{P_1}{P_2}\\<br />2\theta&=&\ln\frac{P_1}{P_2}\\<br />{e}^{2\theta}&=&\frac{P_1}{P_2}=\frac{E_1 I_1}{E_2 I_2}=\frac{Z_{i2}{E_1}^2}{Z_{i1}{E_2}^2}=\frac{Z_{i1}{I_1}^2}{Z_{i2}{I_2}^2}\\<br />{e}^{\theta}&=&\pm\sqrt{{e}^{2\theta}}=\pm\sqrt{\frac{P_1}{P_2}}=\pm\sqrt{\frac{E_1 I_1}{E_2 I_2}}=\pm\sqrt{\frac{Z_{i2}{E_1}^2}{Z_{i1}{E_2}^2}}=\pm\frac{E_1}{E_2}\sqrt{\frac{Z_{i2}}{Z_{i1}}}=\pm\frac{I_1}{I_2}\sqrt{\frac{Z_{i1}}{Z_{i2}}}<br />\end{eqnarray}

著者が勝手に定義している式がちゃんと導きだせる。勝手に定義するよりも影像伝搬定数の本来の定義を書けと言いたい。ここでも同様に正負の二つの値が存在するが、受動回路では正極性だけを考える。

自然対数関数(ln)と指数関数(e)は互いに逆関数であるというのを忘れていた人はこれを機会に思い出して欲しい。自分も良く判っていなかったのは内緒だ。

さて次ぎに著者が示す式も、いきなり結論だけの提示なので、どうやったらそうなるのかついて行けそうもなくなる。

Zi1,Zi2については先の影像インピーダンスの時に導いた式より

\begin{eqnarray}<br />{Z_{i1}}^2&=&\frac{A B}{C D}\\<br />Z_{i1}&=&\pm\sqrt{\frac{A B}{C D}}\\<br />{Z_{i2}}^2&=&\frac{B D}{A C}\\<br />Z_{i2}&=&\pm\sqrt{\frac{B D}{A C}}<br />\end{eqnarray}

ということでよいが。４端子パラメータA,B,C,Dのみで影像伝達定数θを表すにはどうすんだ。

E1/E2とI1/I2の式を導いて先の伝達定数の式に代入すればよさそうである。

実はE1/E2,I1/I2は既に学んだ４端子パラメータの関係式より導くことができる。

\begin{eqnarray}<br />E_1&=&A E_2+B I_2\\<br />&=&A E_2+B \frac{E_2}{Z_{i2}}\\<br />\frac{E_1}{E_2}&=&A+\frac{B}{Z_{i2}}<br />I_1&=&C E_2+D I_2\\<br />&=&C Z_{i2}I_2+D I_2\\<br />\frac{I_1}{I_2}&=&C Z_{i2}+D<br />\end{eqnarray}

これを先のθの式に代入すると

\begin{eqnarray}<br />\theta&=&\frac{1}{2}\ln\frac{P_1}{P_2}\\<br />&=&\ln\sqrt{\frac{P_1}{P_2}}\\<br />&=&\ln\sqrt{\frac{E_1 I_1}{E_2 I_2}}\\<br />&=&\ln\sqrt{\left(A+\frac{B}{Z_{i2}}\right)\left(C Z_{i2}+D\right)}\\<br />&=&\ln\sqrt{A C Z_{i2}+A D+B C+\frac{B D}{Z_{i2}}}<br />\end{eqnarray}

更に先に求めたZi2の式を代入すると

\begin{eqnarray}<br />\theta&=&\ln\sqrt{A C Z_{i2}+A D+B C+\frac{B D}{Z_{i2}}}\\<br />&=&\ln\sqrt{A C \sqrt{\frac{B D}{A C}}+A D+B C+\frac{B D}{\sqrt{\frac{B D}{A C}}}}\\<br />&=&\ln\sqrt{\sqrt{A B C D}+A D+B C+\sqrt{A B C D}}\\<br />&=&\ln\sqrt{A D+2\sqrt{A B C D}+B C}\\<br />&=&\ln\sqrt{\left(\sqrt{A D}+\sqrt{B C}\right)^2}\\<br />&=&\ln\left(\sqrt{A D}+\sqrt{B C}\right)<br />\end{eqnarray}

ということになる。なんだ簡単じゃないか(´∀` )

対称回路の場合にはA=Dとなり、４端子パラメータは実質A,B,Cの３つの独立パラメータから成り

\begin{eqnarray}<br />Z_{i1}&=&Z_{i2}=\sqrt{\frac{B}{C}}\\<br />\theta&=&\ln\left(A+\sqrt{B C}\right)<br />\end{eqnarray}

ということになる。

しかしまたしても次ぎに試練が待っていた。今度は逆にA,B,C,DをZi1,Zi2,θで表せと。しかも著者の示す結論にはまたしても宿敵の双曲線関数が出てくるし、どうすんだこれ。

これに関しては以前に紹介した電気回路の古書「第１級無線技術士用　電気回路（下巻）」に詳しい。それを参考に解いてみよう。

最初に伝達定数の関係を指数関数で表すと

\begin{eqnarray}<br />{e}^{\theta}&=&\sqrt{A D}+\sqrt{B C}<br />\end{eqnarray}

またこの逆数も求めておく

\begin{eqnarray}<br />\frac{1}{{e}^{\theta}}&=&{e}^{-\theta}\\<br />&=&\frac{1}{\sqrt{A D}+\sqrt{B C}}\\<br />&=&\frac{\sqrt{A D}-\sqrt{B C}}{\left(\sqrt{A D}+\sqrt{B C}\right)\left(\sqrt{A D}-\sqrt{B C}\right)}\\<br />&=&\frac{\sqrt{A D}-\sqrt{B C}}{A D-B C}\\<br />&=&\sqrt{A D}-\sqrt{B C}<br />\end{eqnarray}

ここで線形受動回路では相反定理が成り立つのでAD-BC=1となること利用している。

ここまで出そろうと複素双曲線関数の登場

\begin{eqnarray}<br />\sinh\,\theta&=&\frac{{e}^{\theta}-{e}^{-\theta}}{2}\\<br />&=&\frac{\cancel{\sqrt{A D}}+\sqrt{B C}-\left(\cancel{\sqrt{A D}}-\sqrt{B C}\right)}{2}\\<br />&=&\sqrt{B C}\\<br />\cosh\,\theta&=&\frac{{e}^{\theta}+{e}^{-\theta}}{2}\\<br />&=&\frac{\sqrt{A D}+\cancel{\sqrt{B C}}+\left(\sqrt{A D}-\cancel{\sqrt{B C}}\right)}{2}\\<br />&=&\sqrt{A D}<br />\end{eqnarray}

これは複素双曲線関数と指数関数の以下の関係からも自明である。

\begin{eqnarray}<br />{e}^{\theta}&=&\cosh\,\theta+\sinh\,\theta\\<br />&=&\sqrt{A D}+\sqrt{B C}\\<br />{e}^{-\theta}&=&\cosh\,\theta-\sinh\,\theta\\<br />&=&\sqrt{A D}-\sqrt{B C}<br />\end{eqnarray}


先に導いておいたZi1,Zi2の４端子パラメータ表現からZi1*Zi2とZi1/Zi2の関係を導くと

\begin{eqnarray}<br />Z_{i1}Z_{i2}&=&\sqrt{\frac{\cancel{A} B}{C \cancel{D}}}\sqrt{\frac{B \cancel{D}}{\cancel{A} C}}\\<br />&=&\frac{B}{C}<br />\frac{Z_{i1}}{Z_{i2}}&=&\frac{\sqrt{\frac{A \cancel{B}}{\cancel{C} D}}}{\sqrt{\frac{\cancel{B} D}{A \cancel{C}}}}\\<br />&=&\frac{A}{D}<br />\end{eqnarray}

これらの４式を以下の様に組み合わせることで４端子パラメータをZi1,Zi2,θで表すことができる

\begin{eqnarray}<br />A&=&\sqrt{\frac{A}{D}}\sqrt{A D}\\<br />&=&\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta\\<br />B&=&\sqrt{\frac{B}{C}}\sqrt{B C}\\<br />&=&\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta\\<br />C&=&\sqrt{\frac{C}{B}}\sqrt{B C}\\<br />&=&\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta\\<br />D&=&\sqrt{\frac{D}{A}}\sqrt{A D}\\<br />&=&\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta<br />\end{eqnarray}

できたじゃないか(´∀` )

従って対称回路ではA=D,Zi=Zi1=Zi2が成り立つので４端子パラメータはそれぞれ

\begin{eqnarray}<br />A&=&D=\cosh\,\theta\\<br />B&=&Z_{i}\sinh\,\theta\\<br />C&=&\frac{1}{Z_{i}}\sinh\,\theta\\<br />\end{eqnarray}

と表される。

これでやっと影像パラメータで二端子対回路を表すことができる

\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />&=&\left[\begin{array}<br />\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta & \sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta\\<br />\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta & \sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}

対称回路では

\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />\cosh\,\theta & Z_{i}\sinh\,\theta\\<br />\frac{1}{Z_{i}}\sinh\,\theta & \cosh\,\theta<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}

ということになる。実はこれ後に学ぶ分布定数回路の伝送路の二端子対回路表現とまったく相似な式となっている。摩訶不思議である。

影像パラメータはどの参考書を読んでも判りづらかったけど、判ってしまえば面白い。以前一端子対回路で途中で投げてしまったインピーダンス関数がcoth(s)となる回路の合成問題の解決の糸口がどうやらつかめそうである。それは後日分布定数回路をマスターしてからのお楽しみにしよう。

ところで著者はもうひとつ終端開放インピーダンス(Zo1,Zo2)と終端短絡インピーダンス(Zs1,Zs2)による関係式を示しているのだが、どうやったらそれが導けるのかわからない。

おそらく、ここまでの結果からだと、伝達定数θが結局４端子パラメータから計算することになってしまうので別の測定可能なパラメータでθを表す必要があるのは確かなのだ。

最初の方で導いたZo1,Zo2,Zs1,Zs2を影像パラメータ表現で表すと

\begin{eqnarray}<br />Z_{o1}&=&\frac{A}{C}\\<br />&=&\frac{\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta}{\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta}\\<br />&=&Z_{i1}\coth\,\theta\\<br />Z_{o2}&=&\frac{D}{C}\\<br />&=&\frac{\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta}{\frac{1}{\sqrt{Z_{i1}Z_{i2}}}\,\sinh\,\theta}\\<br />&=&Z_{i2}\coth\,\theta\\<br />Z_{s1}&=&\frac{B}{D}\\<br />&=&\frac{\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta}{\sqrt{\frac{Z_{i2}}{Z_{i1}}}\,\cosh\,\theta}\\<br />&=&Z_{i1}\tanh\,\theta\\<br />Z_{s2}&=&\frac{B}{A}\\<br />&=&\frac{\sqrt{Z_{i1}Z_{i2}}\,\sinh\,\theta}{\sqrt{\frac{Z_{i1}}{Z_{i2}}}\,\cosh\,\theta}\\<br />&=&Z_{i2}\tanh\,\theta<br />\end{eqnarray}

従って

\begin{eqnarray}<br />\sqrt{\frac{Z_{o1}}{Z_{s1}}}&=&\sqrt{\frac{Z_{i1}\coth\,\theta}{Z_{i1}\tanh\,\theta}}\\<br />&=&\coth\,\theta<br />\sqrt{\frac{Z_{o2}}{Z_{s2}}}&=&\sqrt{\frac{Z_{i2}\coth\,\theta}{Z_{i2}\tanh\,\theta}}\\<br />&=&\coth\,\theta<br />\end{eqnarray}

ううむ、わからない。またしても宿敵のcoth関数が出てきたところで、見当違いな方向に進んでいることは間違いない。

著者の記述を良く読むと、式の中に出てくるインピーダンスとアドミッタンスはそれぞれインピーダンス行列とアドミッタンス行列に由来するもののようだ。どれにしても同じようなものだと思うのだが。

著者の用いているZパラメータはそれぞれFパラメータと影像パラメータで表すと

\begin{eqnarray}<br />Z_{1f}&=&Z_{11}\\<br />&=&\left.\frac{E_1}{I_1}\right|_{I_2=0}\\<br />&=&\frac{A}{C}\\<br />&=&Z_{i1}\coth\,\theta\\<br />&=&Z_{o1}\\<br />Z_{1s}&=&\frac{1}{Y_{11}}\\<br />&=&\left.\frac{E_1}{I_1}\right|_{E_2=0}<br />&=&\frac{B}{D}\\<br />&=&Z_{i1}\tanh\,\theta\\<br />&=&Z_{s1}\\<br />Z_{2f}&=&Z_{22}\\<br />&=&\left.\frac{E_2}{I_2}\right|_{I_1=0}\\<br />&=&\frac{D}{C}\\<br />&=&Z_{i2}\coth\,\theta\\<br />&=&Z_{o2}\\<br />Z_{2s}&=&\frac{1}{Y_{22}}\\<br />&=&\left.\frac{E_2}{I_2}\right|_{E_1=0}\\<br />&=&\frac{B}{A}\\<br />&=&Z_{i2}\tanh\,\theta<br />&=&Z_{s2}<br />\end{eqnarray}

従ってこれから著者の以下の式が成り立つことまでは良い

\begin{eqnarray}<br />Z_{01}&=&\sqrt{\frac{A B}{C D}}=\sqrt{\frac{Z_{11}}{Y_{11}}}=\sqrt{Z_{1f}Z_{1s}}\\<br />Z_{02}&=&\sqrt{\frac{D B}{C A}}=\sqrt{\frac{Z_{22}}{Y_{22}}}=\sqrt{Z_{2f}Z_{2s}}<br />\end{eqnarray}

問題は著者が結論として示す以下の関係式

\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}=\sqrt{Z_{11}Y_{11}}=\sqrt{Z_{22}Y_{22}}=\sqrt{\frac{Z_{1f}}{Z_{2s}}}=\sqrt{\frac{Z_{2f}}{Z_{2s}}}<br />\end{eqnarray}

どうも成り立っていないように思えるのだが。以下の様だったら問題ないのだが

\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}\\<br />\coth\,\theta&=&\sqrt{Z_{11}Y_{11}}=\sqrt{Z_{22}Y_{22}}=\sqrt{\frac{Z_{1f}}{Z_{2s}}}=\sqrt{\frac{Z_{2f}}{Z_{2s}}}<br />\end{eqnarray}

まさか著者がcoshとcothを混同して式を一緒にしてしまったのではあるまいか？　

ということで著者の誤記という結論にしておこう。

対称回路の場合、伝達定数は

\begin{eqnarray}<br />\cosh\,\theta&=&\sqrt{A D}\\<br />&=&A=D<br />\end{eqnarray}

P.S

国内の参考書では、上記の様に入出力電力比の対数から入っているのは小数派で、何故か手間をかけて入出力電圧比と入出力電流比を先に導いて、最終的に伝達定数（入出力電力比）を導き出す回りくどい解説をしているものが手元の古い本で共通に見られた。現在も売られている電気学会編の「電気工学ハンドブック」は酷いことに電圧と電流の伝達定数は示すものの電力に関する伝達定数は出てこない。なにかこの辺に影像パラメータが廃れた原因の一端があるように見える。

P.S

今頃よく見たら最初の影像インピーダンスの説明で、駆動点インピーダンスの説明が間違っていた...orz
フラット表示 前のトピック | 次のトピック

題名 投稿者 日時
   二端子対回路 webadm 2010-5-4 1:49
     インピーダンス行列（Z行列） webadm 2010-5-4 2:58
     アドミッタンス行列（Y行列） webadm 2010-5-7 10:21
     ハイブリッド行列（H行列） webadm 2010-5-7 10:56
     伝送行列(F行列） webadm 2010-5-8 0:56
     二端子対回路の接続 webadm 2010-5-9 11:00
   » 影像パラメータ webadm 2010-5-10 12:46
     反復パラメータ webadm 2010-5-14 12:08
     理想変成器 webadm 2010-5-16 3:48
     理想ジャイレータ webadm 2010-5-16 5:27
     ２等分定理 webadm 2010-5-17 12:55
     伝達イミッタンス webadm 2010-5-19 17:08

投稿するにはまず登録を
 
ページ変換(Google Translation)
EQPlayers
Allakhazam
EQresource VoA Home
Googleish(EN)
Googlean(KO)
Googlchinese(ZH-CN)
Googltwinese(ZH-TW)
Googlussian(RU)
Googlench(FR)
Googlerman(DE)
Googlabic(AR)
Googlindi(HI)
Googluguese(PT)
Googlutch(NL)
Googltarian(IT)
Googlpanish(ES)
Googlinnish(FJ)
Googlwedish(SY)
Googlatian(HR)
Googlzech(CS)
Googlgarian(BG)
Googlpolish(PL)
Googlmanian(RO)
Googlwegian(NO)
Googleek(EL)
Googldanish(DA)
サイト内検索

高度な検索