Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 2端子対回路演習問題

投稿者	スレッド
webadm	投稿日時: 2010-5-26 11:41
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3082	アドミッタンスパラメータと４端子定数次ぎはアドミッタンスパラメータと４端子定数の間の変換式を導く問題。アドミッタンスパラメータ（Y行列）とはなにか思い出すと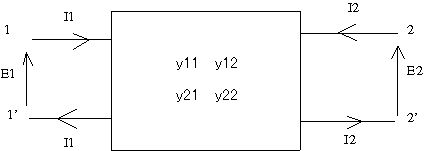上記の回路で $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />y_{11}&=&\left.\frac{I_1}{E_1}\right\|_{E_2=0}\\<br />y_{12}&=&\left.\frac{I_1}{E_2}\right\|_{E_1=0}\\<br />y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}\\<br />y_{22}&=&\left.\frac{I_2}{E_2}\right\|_{E_1=0}<br />\end{eqnarray}$ が成り立つことを表す。一方で４端子対定数(F行列）は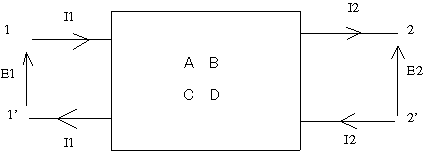上記の回路で $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}<br />\end{eqnarray}$ が成り立つことを意味する。２つの回路ではI2の向きが逆なので注意しながらYパラメータの条件(E2=0,E1=0)をF行列表現の式に適用すると $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />0\\<br />-I_2<br />\end{array}\right]\\<br />E_1&=&\left.-B I_2\right\|_{E_2=0}\\<br />I_1&=&\left.-D I_2\right\|_{E_2=0}\\<br />\left[\begin{array}<br />0\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />-I_2<br />\end{array}\right]\\<br />0&=&\left.A E_2-B I_2\right\|_{E_1=0}\\<br />I_1&=&\left.A E_2-D I_2\right\|_{E_1=0}<br />\end{eqnarray}$ これらの関係からYパラメータは $\begin{eqnarray}<br />y_{11}&=&\left.\frac{I_1}{E_1}\right\|_{E_2=0}\\<br />&=&\left.\frac{-D I_2}{-B I_2}\right\|_{E_2=0}\\<br />&=&\frac{D}{B}\\<br />y_{12}&=&\left.\frac{I_1}{E_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{C E_2-D I_2}{\frac{B}{A}I_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{\frac{C B}{A}I_2-D I_2}{\frac{B}{A}I_2}\right\|_{E_1=0}\\<br />&=&\frac{C B - A D}{B}\\<br />&=&-\frac{A D- B C}{B}<br />y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}\\<br />&=&\left.\frac{-\frac{E_1}{B}}{E_1}\right\|_{E_2=0}\\<br />&=&-\frac{1}{B}\\<br />y_{22}&=&\left.\frac{I_2}{E_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{\frac{A}{B}E_2}{E_2}\right\|_{E_1=0}\\<br />&=&\frac{A}{B}\\<br />\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{D}{B} & -\frac{A D- B C}{B}\\<br />-\frac{1}{B} & \frac{A}{B}<br />\end{array}\right]<br />\end{eqnarray}$ とFパラメータ要素で表される。同様にFパラメータの条件でFパラメータをYパラメータで書き直しても良いが、上記の関係式をFパラメータに付いて解くと $\begin{eqnarray}<br />A&=&-\frac{y_{22}}{y_{21}}\\<br />B&=&-\frac{1}{y_{21}}\\<br />C&=&-\frac{y_{11}y_{22}}{y_{21}}+\frac{y_{12}}{y_{21}}\\<br />&=&\frac{y_{12}y_{21}-y_{11}y_{22}}{y_{21}}\\<br />&=&-\frac{y_{11}y_{22}-y_{12}y_{21}}{y_{21}}\\<br />D&=&-\frac{y_{11}}{y_{21}}\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />-\frac{y_{22}}{y_{21}} & -\frac{1}{y_{21}}\\<br />-\frac{y_{11}y_{22}-y_{12}y_{21}}{y_{21}} & -\frac{y_{11}}{y_{21}}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。 P.S 最初同じ要領でFパラメータをYパラメータで表すことを試みたらどうも結果がおかしいので、先に導いたYパラメータをFパラメータで表した関係から逆に導いたのだが、よく見たら理論の時のFパラメータ条件をI2=0ではなくI1=0と誤記していたのが原因だった。それで矛盾が生じたというわけである。なのでFパラメータの条件(I2=0とE2=0)をYパラメータの回路に当てはめてI2の極性に注意すれば同じ結果が得られるはずである。あと、線形代数をうまく使って同じ結果が得られると思うのだが、これも読者の課題としよう(´∀` ) P.S 後の問題でここの解を利用したらおかしな結果にしかならないので、良くみたら式の途中で痛恨の転記ミス発見(;´Д`) (2010/05/30) Y-F変換の導出過程でCの最初の式に転記ミスがあったのを今更修正 2012/11/4)

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
2端子対回路演習問題	webadm	2010-5-20 4:53
インピーダンスパラメータ	webadm	2010-5-20 5:54
インピーダンスパラメータとアドミッタンスパラメータ	webadm	2010-5-22 23:43
インピーダンスパラメータとハイブリッドパラメータ	webadm	2010-5-23 1:32
インピーダンス行列とアドミッタンス行列	webadm	2010-5-23 10:12
T形回路	webadm	2010-5-23 16:25
続：T形回路	webadm	2010-5-23 16:33
π形回路	webadm	2010-5-23 17:20
Zobel変換	webadm	2010-5-23 17:58
ハイブリッドパラメータ	webadm	2010-5-24 17:53
» アドミッタンスパラメータと４端子定数	webadm	2010-5-26 11:41
伝送行列	webadm	2010-5-26 14:34
T形回路の伝送行列	webadm	2010-5-26 15:14
4端子定数	webadm	2010-5-27 3:18
続：伝送行列	webadm	2010-5-27 13:50
続：４端子定数	webadm	2010-5-27 22:14
続々：４端子定数	webadm	2010-5-29 3:39
インピーダンス行列	webadm	2010-5-29 11:27
アドミッタンス行列	webadm	2010-5-29 11:57
またまた：４端子定数	webadm	2010-5-30 11:15
二端子対回路の並列接続	webadm	2010-5-30 12:37
もうひとつの：４端子定数	webadm	2010-5-30 12:45
アドミッタンスパラメータ	webadm	2010-6-3 12:42
まだまだ：４端子定数	webadm	2010-6-5 13:04
影像パラメータと４端子定数	webadm	2010-6-5 13:44
影像パラメータ	webadm	2010-6-12 22:30
続：影像パラメータ	webadm	2010-6-13 5:07
続々：影像パラメータ	webadm	2010-6-17 5:13
影像インピーダンス	webadm	2010-6-17 16:21
続：影像インピーダンス	webadm	2010-6-17 19:40
まだまだ：影像パラメータ	webadm	2010-6-22 18:50
もうひとつの：影像パラメータ	webadm	2010-6-25 21:54
４端子定数と影像インピーダンス	webadm	2010-6-26 0:45
インピーダンス整合	webadm	2010-6-26 11:27
もうひとつの：影像インピーダンス	webadm	2010-6-26 21:55
反復インピーダンスと４端子定数	webadm	2010-6-27 0:05
反復パラメータ	webadm	2010-6-28 21:04
影像インピーダンスと反復インピーダンス	webadm	2010-6-29 18:16
π形回路の伝送行列、影像パラメータ、反復パラメータ	webadm	2010-7-8 21:06
相互誘導回路と理想変成器	webadm	2010-7-28 6:11
Norton変換	webadm	2010-8-17 10:44
続：Norton変換	webadm	2010-8-17 20:48
容量性変成器	webadm	2010-8-18 3:42
抵抗性変成器	webadm	2010-8-21 10:11
理想ジャイレーター	webadm	2010-10-31 3:26
続：理想ジャイレータ	webadm	2010-11-19 2:41
続々：ジャイレータ	webadm	2010-11-23 21:29
対称回路	webadm	2010-11-25 9:18
続：対称回路	webadm	2010-11-30 0:01
続々：対称回路	webadm	2010-11-30 9:27
またまた：対称回路	webadm	2010-11-30 23:28
軸対称二端子対回路	webadm	2010-12-3 8:26
一方向性回路	webadm	2010-12-8 9:13
続：一方向性回路	webadm	2010-12-8 10:37
Zパラメータ	webadm	2010-12-9 22:51
続：Zパラメータ	webadm	2010-12-10 0:17
４端子定数	webadm	2010-12-14 6:51
理想オペアンプ	webadm	2010-12-14 7:03
続々：Zパラメータ	webadm	2010-12-20 10:10
reactance回路	webadm	2010-12-20 22:52
全域通過回路	webadm	2010-12-23 13:53
最小位相推移回路	webadm	2010-12-23 21:54
続：最小位相推移回路	webadm	2011-4-22 7:02
続々：最小位相推移回路	webadm	2011-4-22 9:38

投稿するにはまず登録を