| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2010-6-5 13:44 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
影像パラメータと4端子定数 次ぎの問題は影像パラメータと4端子定数の関係式を導出せよというもの。
すなわち2端子対回路の影像パラメータを4端子定数で、また逆に4端子定数を影像パラメータでそれぞれ表せという意味になる。 理論の時にも一度やったが見通しが悪かったので、見通しの良い線形代数的手法で再挑戦してみよう。 理論の時に一通り導いたはずだが、別のやり方で同じ結果を導こうとすると実は良く解っていなかったということが判明する。前にやったやり方は理解していてすぐ同じように導出できるのだが、解っていないというのは、それが数学の対象としてどんな扱いになるのかという点である。別のやり方を考える場合にそれが解っていないと致命的である。 影像パラメータは2つの影像インピーダンスと伝達定数の3つから成るが、4端子定数が変わればそれに依存して変わっていく、それは数学的対象として見た場合に4端子定数に対して幾何学的に何に相当するのかという点である。確かに影像インピーダンスも伝達定数も定数であり複素数であるのでベクトルとしても良いが、それら解の集合が存在する代数多様体はどんな形をしているのかといった点である。実はそんなことが解っていなかったというか知ろとしてなかったのである。 単純に電気回路の基礎知識というのであればそんなことは気にせずに試験問題のパターンを暗記して短時間に答えを見いだせばよいのだが、実務で今まで誰も考えたことのないような視点で考え直す必要が生じる場合にはそういったスキルは微塵も役にたたない。理数系の人は本質を見抜くことに徹して、応用や重箱の隅(境界領域)の問題には興味を示さない。工学系は応用と重箱の隅が死活問題なのとは大違い。それだからこそ工学系も本質を見抜く力がないと袋小路に陥って抜け出せなくなる。 要は影像パラメータの数学的な本質を知らないと見通しの良い形で関係式を導出することはできないということであった。 この件についてはまだ時間を要するので、先に残りの問題をしばらく並行して進めることにする。これは試験問題ではないので、時間的な制約は設ける必要がないのである。 いずれにしても線形代数的手法は信号処理や先端の工学理論ではもはや避けて通れないため身に付ける必要がある。したがって「理論の時にやってしまったので割愛する」ということでお茶を濁すことにはしたくないつもりである。 ようやく光明が見えた(2010/06/08) 数学者は問題解決の経緯を明かすことめったにないが、ここはおもちゃ箱なので経緯も楽しむ。 最初に上の図の回路を以下の様に行列表記をしてみることからはじめよう。 しかしひとつの式にZ01,Z02,I1,I2と4つの不定元を含むので結局行列を展開して以前やったようにZ01=E1/I1,Z02=E2/I2の式に代入して連立方程式として別途解くということになってしまう。これでは何も変わらない。 一発でZ01なりZ02を見いだすアプローチはないものか。ここ数日の間、新しく購入した線形代数のテキストを読んだり、YoutubeでMITやインドの大学の線形代数の講義を眺めたりしているうちに今朝名案を思いついた。 最初からZ01、Z02の片方を消去する方法があった。それは先の二端子対回路の入出力方向をひっくり返した鏡像回路を元の2端子回路に縦続接続すれば両端の影像インピーダンスがZ01になる。2つの二端子対回路を更にひっくり返せば両端の影像インピーダンスがZ02になる。これで式を立てればZ01かZ02のいずれかしか現れないことになる。 図で表すと やってみよう、二端子対回路の鏡像回路の4端子定数はAとDが逆になるだけなので ということになる。これは線形代数の固有値ー固有ベクトル方程式(eigenvalue-eigenvector equation) である 影像インピーダンスを求める問題は固有ベクトル(eigenvector)を求める問題だったわけである。それを最初に教えてくれれば面倒くさい導出手順を暗記しなくて済むものを。ほとんどの電気回路理論の教科書がこの事実を言及しない(*1)のはただでさえ難解な線形代数とつながってしまうと学生がついてこれなくなることを恐れてのことだろう。確かに学生の頃に線形代数は数学のカリキュラムに入っていたはずだが、準備的な行列と行列式の部分しか記憶に残っていない。固有値と固有ベクトルを身近に感じたのは今朝この発見が生まれて初めてだ。 まあ固有値問題や固有ベクトル(主成分とかスペクトルとも呼ばれる)問題は最先端の工学領域ではありとあらゆるところに存在するので避けて通れない(Googleの検索エンジンの中心にあるPageRankアルゴリズムも固有ベクトル問題の一種のソルバーらしい)。最先端理論を必要としない業務にはそれらは既に解かれているので直面することはない。 線形代数の主題はこの固有値ー固有ベクトル問題なのだが、それを学ぶための準備で大半の時間が費やされてしまって固有値ー固有ベクトル問題にたどり着かないか、最期の講義時間でちょっと出てくる程度だったりする。数学の授業は歴史的な順番ではなく構造的な順番で教えることになるので主題は一番最期に登場する(あるいは時間切れでそこまで進まずに終わってしまう)ことになる。本当は歴史を辿る意味で問題が先にあって、先人がどのようにそれを攻略していったかというのを学ぶやり方もあるのではないかと思う。 いずれ別の機会に紹介するが、最近読んでいる線形代数のテキストはちくま学芸文庫からつい先日復刻されたSerge Langの「ラング線形代数学(上)(下)」である。注文して届いたら文庫本サイズで電車の中やホームでも立ったままいつでも読めるのが嬉しい。それと線形代数の本ではないが岩波文庫にある高木貞治の「近世数学史談」も文庫本なのでずっと持ち歩いて面白く何度も読み返している。高木貞治は数学歴史話の講談師のごとく、まるで18世紀や19世紀の西欧の数学界を見てきたような語り口で生き生きと伝えている(高木貞治は事実戦前ドイツの最先端数学界隈に居て西洋数学の血脈を受け継いで日本に帰国した人と言える)。読む物を19世紀にタイムワープして大数学者と隣り合わせて居るような不思議な体験をさせてくれる。名作で抱腹絶倒、涙無くして読めないそんな本である。かのフェルマー予想を解く鍵となった谷山・志村予想に名を残す谷山豊はこの本を読んだことから数学者を志したらしい。 なんの話しだったったけ。ああ線形代数のテキストね。というわけで市販の入門書では上記の固有値ー固有ベクトル方程式を解く方法についてはページを割いていない。実はこの分野は未だに終わっていない分野ですべてを書ききれない程ある。 固有値問題についてはそれだけのために書かれた専門書がまた別にある。当然ながらそれらも入手済みであるが、紹介はまた別の機会にしよう。 さて次ぎは先の方程式を解いて固有ベクトルの値であるZ01を求めなければならない。 線形代数まだ勉強中なのに、どうすんだこれ(;´Д`) 実はMaximaには変換行列を与えれば固有値ー固有ベクトル方程式を解いてくれる機能が備わっている。実際にやってみると 結果の最初の2つは固有値を表し、次ぎの2つがその多重度、それに固有値に対する固有ベクトルが並んでいる。固有ベクトルは2つあるが、線形受動回路ではZ01の実数部が常に正の値であることから、 ということになる。従ってZ01は と導かれる。 またこの時の固有値に注目すると つまり伝達定数を求める問題は固有値を求める問題である。すなわち影像パラメータを求める問題は固有値ー固有ベクトル問題に帰着する。 Z02についても変換行列の順序を交換すればよいので 従ってZ02は ということになる。 なんだ簡単じゃないか(´∀` ) これだとMaximaがどうやって固有値や固有ベクトルを導いているか皆目わからないので、先の固有ベクトル方程式を自分で解いてみよう。 それに先だって線形代数を固有値問題まで勉強しないと(;´Д`) 固有値問題は数学的にはかなり事前準備と関連定理や補題が山ほどあるので後回しにして、他に発見された重要な事実について述べておく。 ・非対称な二端子対回路をその鏡像回路と縦続接続すると全体としては対称な二端子対回路になる。 ・この対称な二端子対回路の両端の影像インピーダンスは反復インピーダンスそのものである。 ・縦続接続された二端子対回路が対称回路なら対称回路を縦続接続しても対称な二端子対回路になるから伝搬定数は元の二端子回路の伝搬定数の2倍になる(非対称の場合には2つの異なる方向の伝達定数の和となるのでその平均値が伝達定数となる)。 ・これらのことから反復パラメータ(反復インピーダンス、伝搬定数)を求める問題もまた固有値問題に帰着する 理論の時に影像パラメータと反復パラメータが同じ物であることを直感したのだが、まんざら間違っていなかったようだ。どちらも回路そのものが生来持つ固有値と固有ベクトルで表される。 線形代数の本はどれも数学者が書いたものなので数学的な厳密性や伝統(メンツ)を保っているため、手っ取り早く固有値問題だけ理解したいという工学系の輩には理解不能である。電気回路ではn次元とか一般的な問題は当座は必要なく、二次元行列の固有値問題だけで良いのだが、それだと数学的には意味が無いので講義の時に受講者の関心を引くためのネタに使うことはあってもそれを書物で扱うことはない。あっても帰納法でn=2から順番に試してnが任意の自然数でも成り立つというのを証明するぐらいである。n=2だけでとりあえず十分なんだけど、どうしてもnが任意の一般形を扱う形になってしまう。 それと交流回路では複素数が基本だが数学的には複素数を扱うと実数の場合と同じではないので更に余計な拡張定理を証明していかないといけない。なので入門書の類ではページ数の制約から実数に限定したものも少なくない。実際実数だけで済む応用分野(経済とか統計、ファイナンスとか)も多いのでそれでもそこそこ本が売れる。しかし複素数を元とする場合にそれらがそのまま成り立つかというと厳密には否であるわけで。なんとも微妙なところである。 それと専門的な固有値問題の本では主に代数的に解けない5次元以上の行列を扱う方法が中心的となる。5次元以上の変換行列では特性方程式の次数が5以上になるため代数的には解けない(解の公式が存在しない)ためである。従ってなんらかの反復アルゴリズムによってケースバイケースで解を求めないといけない。それをなるべく有限で短い時間で行う方法が今日まで様々なものが考案されていてその紹介に多くのページが必要となる。これも今のところ二端子対回路では要らない。 なので結局自分でゼロからn=2の行列で複素数を元とする固有値問題の解法を考える必要がある。そんなのは理数系から見ると中途半端な仕事なので誰からも評価されないのは明らかで手を付けないわけだよね。工学系は必要なので各自自分で考えるしかないと。 さてここから影像パラメータを固有値と固有ベクトルから導出してみよう。数学的に厳密な証明を抜きに要点だけをプロットすることにする。線形代数の本では様々なケースについて検討されているが当面今の問題を解く上で必要なもの以外はとりあえず無視する。 最初に疑問に上がるのが固有値や固有ベクトルって何?という点である。これについても一応自分なりに当座納得できる解釈を図で示そう。 先の問題では入力端子対条件を数ベクトルQ、出力端子対条件を数ベクトルPで表したが、元の二端子対回路とその鏡像回路の縦続接続点の端子対条件をR(E3,I3)としよう。元の二端子対回路のF行列をF,その鏡像回路のF行列をFiとするとそれらを縦続接続した回路全体のF行列はL=F.Fiとなる。これらの関係を幾何学的に図で表すと 出力ベクトルPは後段の鏡像回路の変換行列FiによってRに写像され、Rは前段の二端子対回路の変換行列FによってQに写像される。一般にはPとQは変換によって異なる(互いの駆動点インピーダンスがZ01と異なる)ものになると考えられる。 ところが駆動点インピーダンスが他方の端子対に接続されたZ01と等しくなるようにZ01をうまく選ぶことが出来るとすれば、この時のλ=E1/E2=I1/I2が固有値、Z01が固有ベクトルの構成要素に該当する。λとZ01はE1,I1,E2,I2の大きさによらず一意的に回路パラメータから決まることになる。交流回路ではE1,I1,E2,I2は複素数なのでZ01,λも当然ながら複素数定数となるので、実数での固有値と固有ベクトルのようにP,Qが同じ方向を持ちスケール(λ)だけ違うというようにはならないが実数だとすると図のような関係になる。複素数だと説明に苦慮する部分だ。 次ぎの疑問ははたしてそういったZ01が存在するのだろうか?という点である 先の固有値ー固有ベクトル方程式を変形すると を満たす非自明な解が存在しなければならないことを意味する。ここで自明な解とはx=0である。 係数行列に逆行列が存在すると上の式の両辺にその逆行列を乗じると ということになりx=0以外の解は存在しないことになり非自明な解が存在するという前提と矛盾する。したがって非自明な解が存在するには係数行列の逆行列が存在しないことが必要条件となる。 逆行列が存在しないとはどういうことか? それは線形代数の行列と行列式を学んでいればわかる通り、行列式が0となる特異行列(singular matrix)には逆行列が存在しないということである。逆行列の要素の分母は元の行列の行列式となるのでそれが0だと要素が不定となり逆行列が得られないことになる。 その係数行列とその行列式は ということになる。従って行列式の値が0(特異行列)となるλは ということになる。これがこの縦続接続回路の固有値である。 先の固有値ー固有ベクトル方程式でλが既知となって不定元でなくなると残る不定元xに関する斉次方程式となるので固有ベクトルxを解くことができるはずである λ1,λ2についてそれぞれ固有ベクトルxを解くと ということになる。これは実数部が負なので線形受動回路の影像インピーダンスとしてはあり得ない。 同様にλ2に対する固有ベクトルを解くと ということになり、今度は実数部が正なのでこれが影像インピーダンスの片割れということになる。 同様に伝達定数θもλ2の自然対数を二分の1したものとして求めることができるのはMaximaで得た結果で既に示した通り。 同様にZ02はもう片割れの縦続接続回路(変換行列の順番を入れ替えたもの)の影像インピーダンスを求めればMaximaで解いたのと同じ結果が得られる。 なんとなく狐につままれた気がしないでもないが。とりあえず今日の時点ではここまでにしておこう。数学的に厳密にこれが影像パラメータと同値かどうかというのを証明していないので仕方がない。ただ固有値ー固有ベクトルとして憶えたほうが導出の見通しが良いのは確かだ。憶えておく必要があるのは「影像パラメータは固有値と固有ベクトルから成る」の一つだけだから。 さてあと残るは4端子定数を影像パラメータで表すという問題。 理論を学んだ時になんとか姑息な手段で導くことはできたが、もっと見通しの良い方法はないものだろうか? すでに影像パラメータを4端子定数で表した以下の関係式を得ているので、これを4端子定数に関する連立方程式として解けばよさそうに一見思える しかしこれをMaximaに与えて解かせてみると解けない。理論の時にやったようにヒューリスティックな思考錯誤方法なら解は見いだせる。しかしやってみないと解らない方法では見通しが悪すぎる。 別のアプローチとして固有値ー固有ベクトル方程式を以下の様に行列展開すると これらの結果から以下の連立方程式が得られる これをMaximaに与えて解くと という結果が得られる。Maximaではさすがに複素双曲線関数で置き換えるところまではやってくれないので、自分で整理すると 線形受動回路ではB,Cの実数部は常に正でなければならないので後者が解となる。 題意では影像インピーダンスを4端子定数で表すことだけ求めていたのでこれは余分だったかもしれない。 Maximaは簡単に解いてしまうが、手計算で解こうとするとA,B,C,Dに関する二次形式になるため、線形代数的にそっからどうすればいいかわからない。これは読者の課題としよう(´∀` ) P.S 実はMaximaで固有値ー固有ベクトルを求めた結果の形式と合わせるために固有ベクトルの形式を意図的に変形している。自分で計算する分にはx=matrix([Z01],[1])のままで良いのだが、Maximaはx=matrix([1],[1/Z01])の形にしてしまうようだ。固有ベクトルの標準化とか正規化のたぐいだと思われるがそれ以上詳しいことは現時点ではわからない。 P.S 片方の端子対に接続されたZ01を変化させた場合に他方の端子対から見た駆動点インピーダンスがどのように変化するのかプロットしてみたかったが、Z01は複素平面のあらゆる点を取り得るので、駆動点インピーダンスは複素平面そのものの等角写像となりRiemann面を考える必要がある。時間があったら簡単な非対称2端子対回路を例にやってみたい。どこかでZ01と駆動点インピーダンスがぴったり一致する点が現れるはずである。 P.S (*1)後で良く見たら何度も登場している「回路網理論I」の反復パラメータのところで以下の通りしっかり書いてあった...orz そうだよね。Sパラメータが先に出てきてイメージパラメータと反復パラメータをそこから導出している難しいとこだったので読み飛ばしていた。  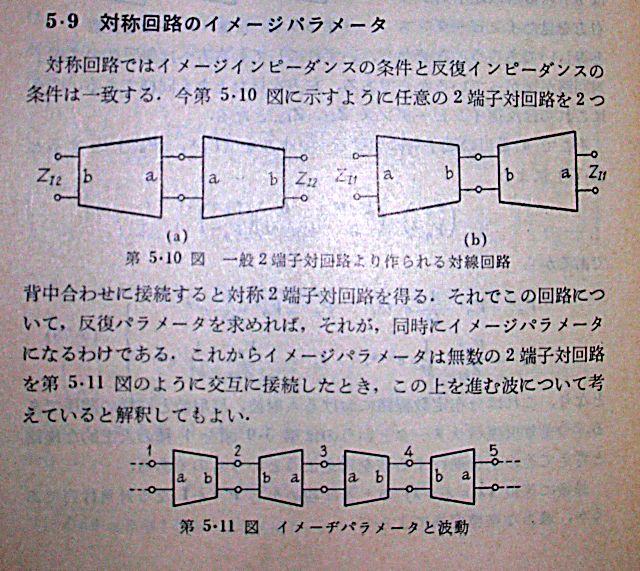 これも独力で同じ着想に到達したのだから良しとしよう。 P.S その後の大学課程「電気回路(2)改訂第3版」では「回路網理論I」にあった固有値や固有ベクトルに関する記述は一切消えている。その間になにか支障があったのだろうか。確かに複素数の固有値ー固有ベクトルは実数のそれと比べて難しく直感的に捉えにくい。特に電気回路では固有ベクトルがそのまま端子対条件とはならないので更に説明がややこしくなる。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2010-5-20 4:53 |
| |
webadm | 2010-5-20 5:54 |
| |
webadm | 2010-5-22 23:43 |
| |
webadm | 2010-5-23 1:32 |
| |
webadm | 2010-5-23 10:12 |
| |
webadm | 2010-5-23 16:25 |
| |
webadm | 2010-5-23 16:33 |
| |
webadm | 2010-5-23 17:20 |
| |
webadm | 2010-5-23 17:58 |
| |
webadm | 2010-5-24 17:53 |
| |
webadm | 2010-5-26 11:41 |
| |
webadm | 2010-5-26 14:34 |
| |
webadm | 2010-5-26 15:14 |
| |
webadm | 2010-5-27 3:18 |
| |
webadm | 2010-5-27 13:50 |
| |
webadm | 2010-5-27 22:14 |
| |
webadm | 2010-5-29 3:39 |
| |
webadm | 2010-5-29 11:27 |
| |
webadm | 2010-5-29 11:57 |
| |
webadm | 2010-5-30 11:15 |
| |
webadm | 2010-5-30 12:37 |
| |
webadm | 2010-5-30 12:45 |
| |
webadm | 2010-6-3 12:42 |
| |
webadm | 2010-6-5 13:04 |
| » |
webadm | 2010-6-5 13:44 |
| |
webadm | 2010-6-12 22:30 |
| |
webadm | 2010-6-13 5:07 |
| |
webadm | 2010-6-17 5:13 |
| |
webadm | 2010-6-17 16:21 |
| |
webadm | 2010-6-17 19:40 |
| |
webadm | 2010-6-22 18:50 |
| |
webadm | 2010-6-25 21:54 |
| |
webadm | 2010-6-26 0:45 |
| |
webadm | 2010-6-26 11:27 |
| |
webadm | 2010-6-26 21:55 |
| |
webadm | 2010-6-27 0:05 |
| |
webadm | 2010-6-28 21:04 |
| |
webadm | 2010-6-29 18:16 |
| |
webadm | 2010-7-8 21:06 |
| |
webadm | 2010-7-28 6:11 |
| |
webadm | 2010-8-17 10:44 |
| |
webadm | 2010-8-17 20:48 |
| |
webadm | 2010-8-18 3:42 |
| |
webadm | 2010-8-21 10:11 |
| |
webadm | 2010-10-31 3:26 |
| |
webadm | 2010-11-19 2:41 |
| |
webadm | 2010-11-23 21:29 |
| |
webadm | 2010-11-25 9:18 |
| |
webadm | 2010-11-30 0:01 |
| |
webadm | 2010-11-30 9:27 |
| |
webadm | 2010-11-30 23:28 |
| |
webadm | 2010-12-3 8:26 |
| |
webadm | 2010-12-8 9:13 |
| |
webadm | 2010-12-8 10:37 |
| |
webadm | 2010-12-9 22:51 |
| |
webadm | 2010-12-10 0:17 |
| |
webadm | 2010-12-14 6:51 |
| |
webadm | 2010-12-14 7:03 |
| |
webadm | 2010-12-20 10:10 |
| |
webadm | 2010-12-20 22:52 |
| |
webadm | 2010-12-23 13:53 |
| |
webadm | 2010-12-23 21:54 |
| |
webadm | 2011-4-22 7:02 |
| |
webadm | 2011-4-22 9:38 |
| 投稿するにはまず登録を | |

