ログイン
ユーザ名:

パスワード:


パスワード紛失

新規登録
Main Menu
Tweet
Facebook
Line
:-?
フラット表示 前のトピック | 次のトピック
投稿者 スレッド
webadm
投稿日時: 2011-5-24 5:11
Webmaster
登録日: 2004-11-7
居住地:
投稿: 3086
定K形フィルタ
いよいよ定Kフィルタについて学ぶことにしよう。

著者は前置きもなく要点だけを解説しているが、それだと天下り的すぎて飲み込みづらいのでValkenburgのNetwork Analysisに書かれている前置きをたどってみよう。

ラダー回路網

ラダー構成は歴史的に重要である。フィルターを構成するために最初に用いられた構造だからだ。それにある種のラダー回路に当てはまることが、格子形回路にも適用できる点である。格子形回路は平衡回路網で構成されたかつてのアナログ電話回路網に不可欠であったためだ。電話網がデジタル化された現代では固定電話の加入者回線網だけが平衡回路として取り残されているだけとなった。

以下の標準的なラダー回路は対称なT字形回路とπ形回路に分解できる。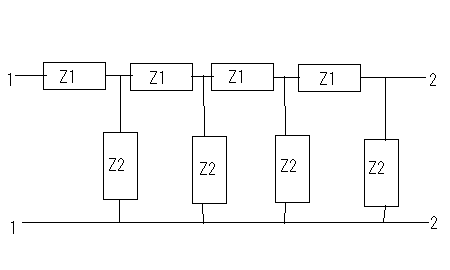



T字形回路に分解すると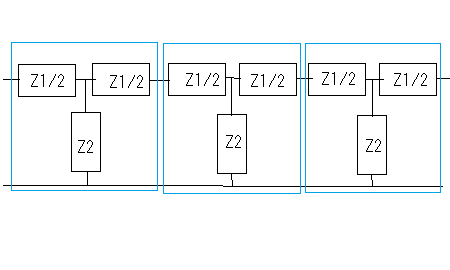



π形回路に分解すると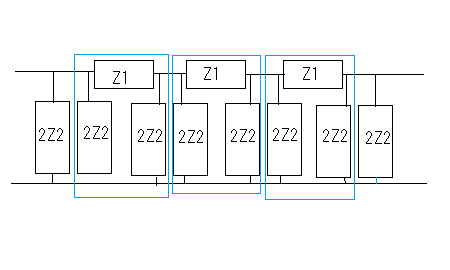



更にこれらのT字形回路とπ形回路は同一のL字形回路だけで構成できる。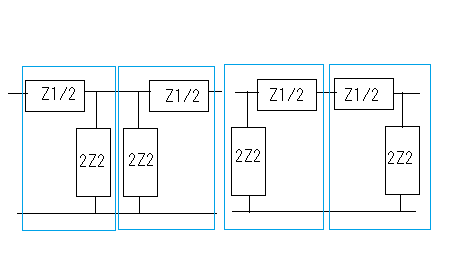



映像インピーダンス

上記のT字回路やπ形回路は左右対称である。L字形回路はそうではない。対称回路か非対称回路のどちらかに適用する公式を導出するために以下の様な非対称T字回路について考える。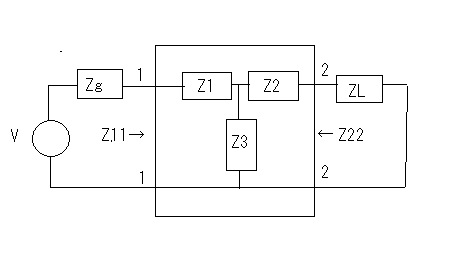



すでにご存じの二端子対回路の映像インピーダンスの定義についてはここでおさらいしよう。ZLを接続し状態で開放端子対1-1から見た駆動点インピーダンスをZ11とし、Zgを接続した状態で開放端子対2-2の駆動点インピーダンスZ22とすると、以下の条件が成り立つ時、端子対1-1と端子対2-2で映像インピーダンス整合がとれていると言う。

Z_g=Z_{11}かつZ_L=Z_{22}

Z11とZ22はそれぞれ二端子対回路の映像インピーダンス(Z1i,Z2i)であることは承知の通り。

上の回路の２つの映像インピーダンスを導くと

\begin{eqnarray}<br />Z_{1i}&=&Z_{11}=Z_1+\frac{1}{\frac{1}{Z_3}+\frac{1}{Z_2+Z_{2i}}}\\<br />&=&Z_1+\frac{\left( Z_{2}+Z_{2i}\right) \,Z_3}{Z_3+Z_2+Z_{2i}}\\<br />Z_{2i}&=&Z_2+\frac{1}{\frac{1}{Z_3}+\frac{1}{Z_1+Z_{1i}}}\\<br />&=&Z_2+\frac{\left( Z_1+Z_{1i}\right) \,Z_3}{Z_3+Z_1+Z_{1i}}<br />\end{eqnarray}

ということになり、Z1iにはZ2iがZ2iにはZ1iが含まれる。映像インピーダンスは上記の２つの式をZ1iとZ2iに関する連立方程式として解くことによっても求めることができるが、二端子対回路のそれぞれの端子対を開放および短絡した状態での駆動点インピーダンス(Z1o,Z1s,Z2o,Z2s)から求めることもできる。

端子対2-2を開放および短絡した時の端子対1-1から見た駆動点インピーダンスはそれぞれ

\begin{eqnarray}<br />Z_{1o}&=&Z_1+Z_3\\<br />Z_{1s}&=&Z_1+\frac{1}{\frac{1}{Z_3}+\frac{1}{Z_2}}\\<br />&=&Z_1+\frac{Z_3 Z_2}{Z_3+Z_2}\\<br />Z_{2o}&=&Z_2+Z_3\\<br />Z_{2s}&=&Z_2+\frac{1}{\frac{1}{Z_3}+\frac{1}{Z_1}}\\<br />&=&Z_2+\frac{Z_3 Z_1}{Z_3+Z_1}<br />\end{eqnarray}

ということになる。詳しい導出方法は二端子対回路の時にやったのでそちらに譲るとして、映像インピーダンスを開放および短絡駆動点インピーダンスで表すと

\begin{eqnarray}<br />Z_{1i}&=&\sqrt{Z_{1o}Z_{1s}}\\<br />Z_{2i}&=&\sqrt{Z_{2o}Z_{2s}}<br />\end{eqnarray}

ということになる。また対称回路では２つの映像インピーダンスは等しいことから

\begin{eqnarray}<br />Z_{1i}&=&Z_{2i}=Z_i<br />\end{eqnarray}

ということになる。これを利用して前出の対称T字形回路の映像インピーダンスを求めると

\begin{eqnarray}<br />Z_{iT}&=&\sqrt{Z_{1o}Z_{1s}}=\sqrt{\left(\frac{Z_1}{2}+Z_2\right)\left(\frac{Z_1}{2}+\frac{Z_2\frac{Z_1}{2}}{Z_2+\frac{Z_1}{2}}\right)}\\<br />&=&\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}<br />\end{eqnarray}

ということになる。同様にして対称π形回路の映像インピーダンスを求めると

\begin{eqn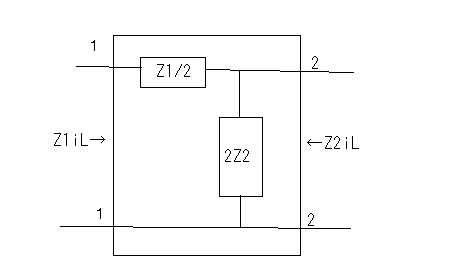array}<br />Z_{i\pi}&=&\sqrt{Z_{1o}Z_{1s}}=\sqrt{\left(\frac{1}{\frac{1}{2 Z_2}+\frac{1}{Z_1+2 Z_2}}\right)\left(\frac{1}{\frac{1}{2 Z_2}+\frac{1}{Z_1}}\right)}\\<br />&=&\sqrt{\left(\frac{2\,Z2\,\left( 2\,Z2+Z1\right) }{4\,Z2+Z1}\right)\left(\frac{2\,Z_1\,Z_2}{2\,Z_2+Z_1}\right)}\\<br />&=&\frac{Z_1 Z_2}{sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}}<br />\end{eqnarray}

ということになる。



今度は対称T字回路と対称π形回路を構成するL字回路の映像インピーダンスを求めると

\begin{eqnarray}<br />Z_{1iL}&=&\sqrt{Z_{1o}Z_{1s}}=\sqrt{\left(\frac{Z_1}{2}+2 Z_2\right)\left(\frac{Z_1}{2}\right)}\\<br />&=&\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}\\<br />Z_{2iL}&=&\sqrt{Z_{2o}Z_{2s}}=\sqrt{\left(2 Z_2\right)\left(\frac{1}{\frac{1}{2 Z_2}+\frac{1}{\frac{Z_1}{2}}}\right)}\\<br />&=&\frac{Z_1 Z_2}{\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}}<br />\end{eqnarray}

ということになる。これは先に求めた対称T字回路と対称π形回路のそれぞれの映像インピーダンスと等しいことがわかる。

\begin{eqnarray}<br />Z_{1iL}&=&Z_{iT}\\<br />Z_{2iL}&=&Z_{i\pi}<br />\end{eqnarray}

映像伝達関数

対称T字形回路を以下の様に両端を映像インピーダンスで終端した場合の入力と出力の電流比を求めると

\begin{eqnarray}<br />\frac{I_1}{I_2}&=&e^{\gamma}=\frac{Z_2+\frac{Z_1}{2}+Z_i}{Z_2}=1+\frac{Z_1}{2 Z_2}+\frac{Z_i}{Z_2}<br />\end{eqnarray}

これをZiについて解くと

\begin{eqnarray}<br />Z_i&=&Z_2\[\left(e^{\gamma}-1\right)-\frac{Z_1}{2 Z_2}\]<br />\end{eqnarray}

先に求めた対称T字形回路の映像インピーダンスと上のZiは等価なので

\begin{eqnarray}<br />Z_{iT}&=&\sqrt{\frac{Z_2}{4}+Z_1 Z_2}\\<br />{Z_{iT}}^2&=&\cancel{\frac{{Z_2}^2}{4}+Z_1 Z_2}\\<br />&=&{Z_2}^2\[\left(e^{\gamma}-1\right)-\frac{Z_1}{2 Z_2}\]^2\\<br />&=&{Z_2}^2\left[\left(e^{\gamma}-1\right)^2-2\left(e^{\gamma}-1\right)\frac{Z_1}{2 Z_2}+\frac{{Z_1}^2}{4{Z_2}^2}\right]\\<br />&=&{Z_2}^2\left(e^{2\gamma}-2e^{\gamma}+1-e^{\gamma}\frac{Z_1}{Z_2}+\frac{Z_1}{Z_2}+\frac{{Z_1}^2}{4{Z_2}^2}\right)\\<br />&=&{Z_2}^2\left(e^{2\gamma}-2e^{\gamma}+1\right)-e^{\gamma}Z_1 Z_2+\cancel{Z_1 Z_2+\frac{{Z_1}^2}{4}}<br />\end{eqnarray}

(2011/7/27)式の展開一部誤りがあったのを訂正。

整理すると

\begin{eqnarray}<br />{Z_2}^2\left(e^{2\gamma}-2e^{\gamma}+1\right)-Z_1 Z_2 e^{\gamma}&=&0\\<br />\frac{e^{2\gamma}-2e^{\gamma}+1}{e^{\gamma}}&=&\frac{Z_1}{Z_2}<br />\end{eqnarray}

ここで

cosh\,\gamma=\frac{1}{2}\left(e^{\gamma}+e^{-\gamma}\right)

であることから

\begin{eqnarray}<br />cosh\,\gamma&=&1+\frac{Z_1}{2 Z_2}<br />\end{eqnarray}

ということになる。また複素双曲線関数の公式

\begin{eqnarray}<br />cosh\,\gamma+sinh\,\gamma&=&e^{\gamma}<br />\end{eqnarray}

と先のcoshの式から

\begin{eqnarray}<br />sinh\,\gamma&=&\frac{Z_1}{Z_2}<br />\end{eqnarray}

従ってtanhは

\begin{eqnarray}<br />tanh\,\gamma&=&\frac{Z_i}{\frac{Z_1}{2}+Z_2}<br />\end{eqnarray}

また映像インピーダンスZiと開放駆動点インピーダンスZ1oは

\begin{eqnarray}<br />Z_i&=&\sqrt{Z_{1s}Z_{1o}}\\<br />Z_{1o}&=&\frac{Z_1}{2}+Z_2<br />\end{eqnarray}

であることから、それぞれ代入すると

\begin{eqnarray}<br />tanh\,\gamma&=&\sqrt{\frac{Z_{1s}}{Z_{1o}}}<br />\end{eqnarray}

ということになる。

ここで映像伝達定数は２つの実数、減衰定数（α）と位相定数（β）からなる複素数であることを二端子対回路の時に学んだのを思いだそう

\begin{eqnarray}<br />\gamma&=&\alpha+j\beta\\<br />tanh\,\gamma&=&\frac{sinh\,\gamma}{cosh\,\gamma}=\frac{sinh\left(\alpha+j\beta\right)}{cosh\left(\alpha+j\beta\right)}\\<br />&=&\frac{sinh\,\alpha\,cos\,\beta+j\,cosh\,\alpha\,sin\,\beta}{cosh\,\alpha\,cos\,\beta+j\,sinh\,\alpha\,sin\,\beta}<br />\end{eqnarray}

分子と分母を共にcoshαcosβで割ると

\begin{eqnarray}<br />tanh\,\gamma&=&\frac{\frac{sinh\,\alpha}{cosh\,\alpha}+j\frac{sin\,\beta}{cos\,\beta}}{1+j\frac{sinh\,\alpha}{cosh\,\alpha}\frac{sin\,\beta}{cos\,\beta}}\\<br />&=&\frac{tanh\,\alpha+j\,tan\,\beta}{1+j\,tanh\,\alpha\,tan\,\beta}<br />\end{eqnarray}

ということになる。なんだよそんなの当たり前じゃんと一瞬退屈な数式の操作に思えたのだが、ここからやっと昔の人の知恵に感嘆させられることになる。

概説の時に原始的なネットワークアナライザーが登場したがそのときは昔の人がどうやってフィルタの通過域と減衰域、それに遮断周波数(cutoff frequency)を予測するかという知恵に驚かされた。

おそらくフィルタ研究の歴史の初期は思考錯誤で目的の特性を備えたフィルター回路をどうやって構成するか大問題だったに違いない。

考えられたのは通過域では減衰定数αは０となること、減衰域ではα≠0となることは明らかなので、それを先の伝達定数の式に適用すると

\begin{eqnarray}<br />\left. tanh\,\gamma\right|_{\alpha=0}&=&\frac{tanh\,0+j\,tan\,\beta}{1+j\,tanh\,0\,tan\,\beta}\\<br />&=&j\,tan\,\beta<br />\end{eqnarray}

すなわち通過域ではtanhγは純虚数となることがわかる。

同様に位相定数β＝0,±π、±2π,...では

\begin{eqnarray}<br />\left. tanh\,\gamma\right|_{\beta=0,\pm\pi,\pm 2\pi,\dots}&=&\frac{tanh\,\alpha+j\,tan\,0}{1+j\,tanh\,\alpha\,tan\,0}\\<br />&=&tanh\,\alpha<br />\end{eqnarray}

従ってtanhγは実数となる。

もうひとつtanβが∞となるβ＝±π/2,±3π/2,±5π/2,...では

\begin{eqnarray}<br />\left. tanh\,\gamma\right|_{\beta=\pm\frac{\pi}{2},\pm\frac{3\pi}{2},\pm\frac{5\pi}{2},\dots}&=&\frac{tanh\,\alpha+j\,tan\,\frac{\pi}{2}}{1+j\,tanh\,\alpha\,tan\,\frac{\pi}{2}}\\<br />&=&\frac{\frac{tanh\,\alpha}{tan\,\frac{\pi}{2}}+j}{\frac{1}{tan\,\frac{\pi}{2}}+j\,tanh\,\alpha}\\<br />&=&\frac{1}{tanh\,\alpha}<br />\end{eqnarray}

したがってtanhγは実数をとる。

ここではLとCのみから成るリアクタンス回路に限定すると、tanhγは実数か純虚数のいずれかしか取り得ない。映像インピーダンスおよび映像伝達定数の開放駆動点インピーダンスと短絡駆動点インピーダンスの関係から

\begin{eqnarray}<br />Z_i&=&\sqrt{Z_{1o}Z_{1s}}=\sqrt{\left(\pm j X_{1o}\right)\left(\pm j X_{1s}\right)}\\<br />tanh\,\gamma&=&\sqrt{\frac{Z_{1s}}{Z_{1o}}}=\sqrt{\frac{\pm j X_{1s}}{\pm j X_{1o}}}<br />\end{eqnarray}

以下の組み合わせ条件からそれが明らか。

\begin{eqnarray}<br />\begin{array}Case & X_{1s} & X_{1o} & Z_i & tanh\,\gamma \\<br />1 & \plus & \plus & j X_i & real \\<br />2 & \minus & \minus & j X_i & real \\<br />3 & \plus & \minus & R_i & imaginary \\<br />4 & \minus & \plus & R_i & imaginary \end{array}<br />\end{eqnarray}

従って減衰定数と位相定数との関係も以下の４つのケース

\begin{eqnarray}<br />\begin{array}Case & j X_{1s} & j X_{1o} & Z_i & tanh\,\gamma & \alpha & \beta \\<br />1 & + & + & j X_i & real & \alpha\ne 0 & 0\, or\, \frac{\pi}{2} \\<br />2 & - & - & j X_i & real & \alpha\ne 0 & 0\, or\, \frac{\pi}{2} \\<br />3 & + & - & R_i & imaginary & 0 & \beta\ne 0 \\<br />4 & - & + & R_i & imaginary & 0 & \beta\ne 0 \end{eqnarray}<br />\end{eqnarray}

ここでようやく映像伝達定数とフィルタ理論の結びつきが見えたことになる。やはり二端子対回路と古典フィルタ理論は一緒に学ばないと意味がない。古典フィルタ理論だけ切り捨てると講義時間は短くてすみ、講義も要領良くまとまるかもしれないが、まったく無味乾燥なものとなるだけだ。

ここでようやく通過域（α＝０）では映像インピーダンスが実数となり、減衰域では純虚数となることがわかる。

そこで対称T字回路と対称π形回路の映像インピーダンスを以下の様に変形すると

\begin{eqnarray}<br />Z_{iT}&=&\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}=\sqrt{Z_1 Z_2\left(1+\frac{Z_1}{4 Z_2}\right)}\\<br />Z_{i\pi}&=&\frac{Z_1 Z_2}{\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}}=\sqrt{\frac{Z_1 Z_2}{1+\frac{Z_1}{4 Z_2}}}<br />\end{eqnarray}

ということになる。

通過域と減衰域の境界（遮断周波数：cutoff frequency）では映像インピーダンスが実数と純虚数の間を変化する点であるので、上の映像インピーダンスの式で

\begin{eqnarray}<br />1+\frac{Z_1}{4 Z_2}&=&0\\<br />\frac{Z_1}{4 Z_2}&=&-1<br />\end{eqnarray}

となる特異点を境に映像インピーダンスが実数と純虚数の間を変化することになる。すなわち通過域と減衰域の境界線である遮断周波数の条件ということになる。

まだ定K形フィルタが登場するのに露払いが少々残っている。

最近本を手に取って読もうとすると細かい字が判別できなくなった。連日眼精疲労がたまって左目が特に視力が低下している。しかし本をホテルのベッドの上に置いて、ベット脇の椅子に座った位置から見下ろして読む分にはまったく問題無い。記号の小さな添え字もはっきり見える。なんだ最初からそうすればよかった（´∀｀　）

映像インピーダンスが通過域では実数（抵抗)になって減衰域では純虚数（リアクタンス）になるということは、賢明な読者なら既に察しの通り、電力が出力側へ移動するか反射するかの違いを意味する。概説の時に描いた等価電圧源を出力側に持つ回路図で考えるといろいろなケースでも納得がいく。もともと出力側の等価電圧源の電圧は対称回路の場合には映像伝達定数と入力側の電源電圧によって決まる。通過域では入力と同じ（α＝０）、減衰域では減衰（α≠0)するということになる。

古典フィルタ理論は意図した通過域で実数をとり、減衰域で純虚数をとるような映像インピーダンスを設計すればよいことになる。これが古典フィルタが映像インピーダンスに基づいて設計されると言われる所以だった。わかってしまえば当たり前なのだが、単純に天下りに言われてもピンとこない。

さて残る対称T字形回路の議論を再開しよう。

前半に登場した以下の式からまた別の映像伝達関数の式が導かれることを示そう。

\begin{eqnarray}<br />cosh\,\gamma&=&1+\frac{Z_1}{2 Z_2}\\<br />\frac{cosh\,\gamma-1}{2}&=&\frac{Z_1}{4 Z_2}\\<br />&=&sinh^2\,\frac{\gamma}{2}=\frac{Z_1}{4 Z_2}<br />\end{eqnarray}

再びγ=α+jβを代入すると

\begin{eqnarray}<br />sinh\,\frac{\alph+j\beta}{2}&=&sinh\,\frac{\alpha}{2}\,cos\,\frac{\beta}{2}+j\,cosh\,\frac{\alpha}{2}\,sin\,\frac{\beta}{2}=\sqrt{\frac{Z_1}{4 Z_2}}<br />\end{eqnarray}

LC二端子対回路ではZ1およびZ2はいずれも容量性もしくは誘導性リアクタンスであるので

\begin{eqnarray}<br />Z_1&=&\pm j X_1\,\,Z_2=\pm j X_2<br />\end{eqnarray}

Z1とZ2が互いに正負逆の場合には、Z1/4Z2は負の値をとるためそのべき根は純虚数となる、従って

\begin{eqnarray}<br />sinh\,\frac{\alpha}{2}\,cos\,\frac{\beta}{2}&=&0\\<br />cosh\,\frac{\alpha}{2}\,sin\,\frac{\beta}{2}&=&\sqrt{\frac{-Z_1}{4 Z_2}}<br />\end{eqnarray}

という関係が成り立つことを意味する。

これを満たすαとβの解の集合は、α=0もしくはβ=±π,±3π,...の二通りあり、

\begin{eqnarray}<br />\alpha&=&0\\<br />\beta&=&2\,sin^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}}<br />\end{eqnarray}

もしくは

\begin{eqnarray}<br />\beta&=&\pm\pi,\pm 3 \pi,\pm 5\pi,\dots\\<br />\alpha&=&2\,cosh^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}}<br />\end{eqnarray}

ということになる。

一方Z1/4Z2が正となる場合、そのべき根は実数となるので今度は

\begin{eqnarray}<br />cosh\,\frac{\alpha}{2}\,sin\,\frac{\beta}{2}&=&0\\<br />sinh\,\frac{\alpha}{2}\,cos\,\frac{\beta}{2}&=&\sqrt{\frac{Z_1}{4 Z_2}}<br />\end{eqnarray}

この場合にはαの解の集合に0は含まれない。これらの条件を満たすのは唯一βが0,±2π、...をとるときである。

\begin{eqnarray}<br />\beta&=&0,\pm 2\pi,\pm 4\pi,\dots\\<br />\alpha&=&2 sinh^{-1}\,\sqrt{\frac{Z_1}{4 Z_2}}<br />\end{eqnarray}

従って

\begin{eqnarray}<br />\begin{array}\le\frac{Z_1}{4 Z_2} & \ge\frac{Z_1}{4 Z_2} & band & \alpha & \beta \\ \hline \\<br />-\infty & -1 & stop & 2 cosh^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}} & \pm\pi,\pm 3\pi,\dots \\<br />-1 & 0 & pass & 0 & 2 sin^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}} \\<br />0 & \infty & stop & 2 sinh^{-1}\,\sqrt{\frac{Z_1}{4 Z_2}} & 0,\pm 2\pi,\pm 4\pi,\dots \end{array}<br />\end{eqnarray}

ということになる。(2011/06/20 一部訂正）

これは映像伝達関数の式を-Z1/4Z2をパラメータとして変化させた場合に減衰定数αと位相定数βの解の集合を求めたことを意味する。これは数学的な視点なくしてはいくら試行錯誤で実験や測定を繰り返しても到達できない。

これでようやく定K形フィルタを登場させる舞台準備が整った。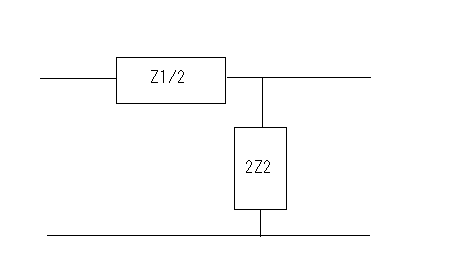



これまでの対称T字回路や対称π形回路、それを構成する上のL字形回路のZ1,Z2が

\begin{eqnarray}<br />\frac{Z_1}{2}2 Z_2&=&Z_1 Z_2=R^2<br />\end{eqnarray}

なる条件を満たすように設計されたものは定K形フィルタと呼ばれる。

Zobelが最初に発表した時は上の式でRの代わりにKが使用されたことから定K形フィルタと称されるようになった。ものの本によっては忠実にKもしくはkをRの代わりに使用している。kは実数定数の意味合いが強いが、実際には単位がZ1,Z2と同じΩであるためインピーダンス値が実数をとるRを使用するのがより適切ということだろう。このRを終端抵抗として使用した場合に通過域で最大電力が伝達されることはこれまでの映像インピーダンスの解析結果から明らかである。

ほとんどの電気回路の参考書は、定K形フィルタの解説をここから出発するので難解なものになっている。やはりこれまでの議論の延長線上でValkenburgの解説を追うことにしよう。

これまで映像伝達関数の解析で用いたZ1/4Z2をここで改めて新しいパラメータとして再登場させることになる。

\begin{eqnarray}<br />x^2&=&\frac{-Z_1}{4 Z_2}<br />\end{eqnarray}

負号が付いているのは、x^2が正の実数となるようにするためで、実際にZ1とZ2は一方が容量性であれば他方は誘導性リアクタンスでなければ先の定K形フィルタの条件式を満足しないからである。

\begin{eqnarray}<br />Z_1 Z_2&=&\left(\pm j X_1\right)\left(\mp j X_2\right)=+X_1 X_2=R^2<br />\end{eqnarray}

今度はRとxを使って最後に登場した映像インピーダンスの式を書き換えると

\begin{eqnarray}<br />Z_{iT}&=&\sqrt{Z_1 Z_2\left(1+\frac{Z_1}{4 Z_2}\right)}=R\sqrt{1-x^2}\\<br />Z_{i\pi}&=&\sqrt{\frac{Z_1 Z_2}{1+\frac{Z_1}{4 Z_2}}}=\frac{R}{\sqrt{1-x^2}}<br />\end{eqnarray}

ということになる。

最後の表にあるように-Z1/4Z2が正の値をとるケースでは減衰域となり

\begin{eqnarray}<br />\alpha&=&2\,cosh^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}}=2\,cosh^{-1}\,x\\<br />\beta&=&\pm\pi,\pm 3\pi,\dots<br />\end{eqnarray}

ということになる。同様に通過域では

\begin{eqnarray}<br />\alpha&=&0\\<br />\beta&=&2\,sin^{-1}\,\sqrt{\frac{-Z_1}{4 Z_2}}=2\,sin^{-1}\,x<br />\end{eqnarray}

ということになる。

Valkenburgの議論では対称T字回路と対称π形回路とそれらを共通に構成する非対称逆L字回路を含めてZ1とZ2が先の定K形フィルタの条件を満たす限り定K形フィルタに含まれるのである。既に触れた通りに逆L字回路の２つの映像インピーダンスは、逆L字回路を向かい合わせおよび背中合わせに縦続接続した対称T字回路と対称π形回路の映像インピーダンスと等しいからである。このことは二端子対回路の時に映像インピーダンスを学んだ時に既に承知の通り。

多くの電気回路の本では逆L字回路だけを取り上げて定K形フィルタとして解説している。

著者の場合は、回路図から見てわかるとおり逆L字回路のそれはValkenburgの議論で出てくるものと同じでシリーズインピーダンスがZ1/2でシャントインピーダンスが2Z2となっている。注釈欄でValkenburgと同じように対称T字回路や対称π形回路が同じ逆L字回路から構成されることを示している。ただし回路解析そのものは、他の参考書と同じように逆L字回路に限定したものとなっている。

さて次に登場するのは難解な映像インピーダンス、減衰定数、位相定数をパラメータを変化させてプロットしたグラフである。

映像インピーダンスは複素数なのであるパラメータに従ってプロットするのが難しい。それは周波数でも先のxでも同じである。周波数によってxは0から∞の範囲をとる。それに対して映像インピーダンスは実軸と虚軸上をたどる。しかしこれだと座標軸上を移動するだけなのでわかりづらい。なので絶対値をパラメータに従ってプロットすることになる。しかしMaximaでは簡単にはプロットできない。

しかたないので実軸上に写像する関数と虚軸に写像する関数の２つに分離してプロットする必要があった。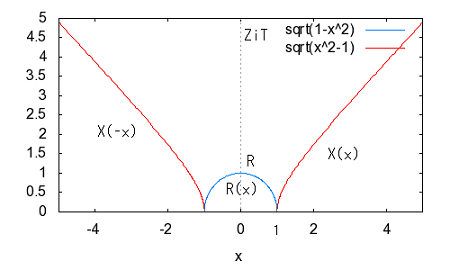



簡単そうで実際にプロットしようとするとわかる先人の苦労。

今度は対称π形回路の映像インピーダンスのプロット。これを見るとValkenburgの同じプロットはR(x)が放物線状だが、実際にプロットするとそうではないことがわかる。極の前後の傾きは実際にはかなり急峻である。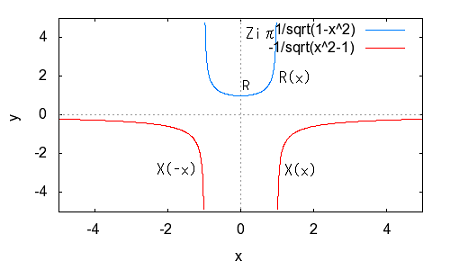



続いて減衰定数αのプロット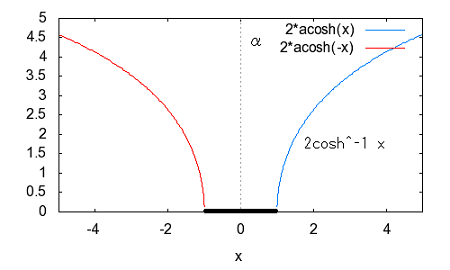



最後が位相定数βのプロット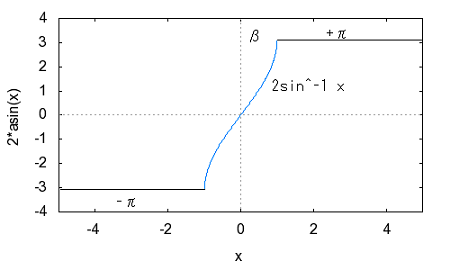



大抵の電気回路の本ではパラメータxの代わりに遮断周波数と周波数の比を使用している。実それはここまでの過程を端折っただけのことで、本当はこの後で登場する。

ここで扱っている標準的な対称T字回路、対称π形回路それを構成する逆L字回路の遮断角周波数ω0はZ1=jωL、Z2=1/jωCとすると

\begin{eqnarray}<br />Z_1&=&j\omega L\,\,Z_2=\frac{1}{j\omega C}\\<br />1+\frac{Z_1}{4 Z_2}&=&1+\frac{j\omega L}{4\frac{1}{j\omega C}}\\<br />&=&1-\frac{{\omega}^2 L C}{4}<br />&=&0\\<br />\omega_0&=&\frac{2}{\sqrt{L C}}<br />\end{eqnarray}

ということになる。従って先のパラメータxは

\begin{eqnarray}<br />x&=&\sqrt{\frac{-Z_1}{4 Z_2}}=\sqrt{\frac{-j\omega L}{4\frac{1}{j\omega C}}}=\sqrt{\frac{{\omega}^2}{\frac{4}{L C}}}\\<br />&=&\frac{\omega}{\omega_0}<br />\end{eqnarray}

ということになる。従ってこの場合の対称T字回路の減衰定数と位相定数は遮断角周波数によって

\begin{eqnarray}<br />\alpha&=&0,\,\,\,\beta=2\,sin^{-1}\,\frac{\omega}{\omega_0}\,\,\,\left{0\le \omega \le \omega_0\right}\\<br />\alpha&=&2\,cosh^{-1}\,\frac{\omega}{\omega_0},\,\,\,\beta=\pi\,\,\,\left{\omega\ge\omega_0\right}\\<br />\omega_0&=&\frac{2}{\sqrt{L C}}\\<br />R&=&\sqrt{\frac{L}{C}}<br />\end{eqnarray}

ということになる。ここでRは公称インピーダンス(nominal impedance)と呼ばれる。これはω0を遮断角周波数とする低域通過フィルタの例である。

今度は同じ回路でZ1を容量性、Z2を誘導性と逆の関係にすると、パラメータxは

\begin{eqnarray}<br />Z_1&=&\frac{1}{j\omega C}\\<br />Z_2&=&j\omega L\\<br />1+\frac{Z_1}{4 Z_2}&=&1+\frac{\frac{1}{j\omega C}}{4 j\omega L}=1-\frac{1}{4{\omega}^2 L C}\\<br />&=&0\\<br />\omega_0&=&\frac{1}{2\sqrt{L C}}\\<br />x&=&\sqrt{\frac{-Z_1}{4 Z_2}}=\sqrt{\frac{-\frac{1}{j\omega C}}{4 j\omega L}}\\<br />&=&\frac{1}{\sqrt{4{\omega}^2 L C}}\\<br />&=&\frac{\omega_0}{\omega}<br />\end{eqnarray}

ということになる。この場合ωが大きくなるとxが小さくなるため前の低域フィルタと逆は逆になり

\begin{eqnarray}<br />\alpha&=&0,\,\,\,\beta=2\,sin^{-1}\,\frac{\omega_0}{\omega}\,\,\,\left{\omega\ge\omega_0\right}\\<br />\alpha&=&2\,cosh^{-1}\,\frac{\omega_0}{\omega},\,\,\,\beta=\pi\,\,\,\left{0\le\omega\le\omega_0\right}\\<br />\omega_0&=&\frac{1}{2\sqrt{L C}}\\<br />R&=&\sqrt{\frac{L}{C}}<br />\end{eqnarray}

高域通過フィルタとなることがわかる。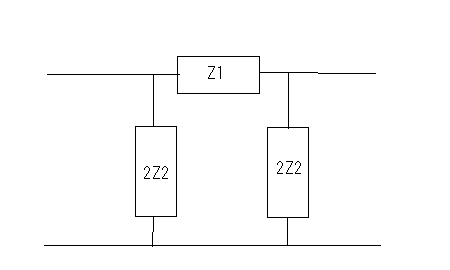



次に対称π形回路ではどうだろう。

\begin{eqnarray}<br />Z_1&=&j\omega L\\<br />Z_2&=&\frac{1}{j\omega C}\\<br />1+\frac{Z_1}{4 Z_2}&=&1+\frac{j\omega L}{4\frac{1}{j\omega C}}\\<br />&=&1-\frac{{\omega}^2 L C}{4}\\<br />&=&0\\<br />\omega_0&=&\frac{2}{\sqrt{L C}}\\<br />x&=&\sqrt{\frac{-Z_1}{4 Z_2}}=\sqrt{\frac{-j\omega L}{4\frac{1}{j\omega C}}}\\<br />&=&\sqrt{\frac{{\omega}^2 L C}{4}}\\<br />&=&\frac{\omega}{\omega_0}\\<br />R&=&\sqrt{\frac{L}{C}}<br />\end{eqnarray}

ということで対称T字回路と同様の遮断角周波数や公称インピーダンスは同じである。映像インピーダンスや減衰定数、位相定数のプロットが先に示したように対称T字回路のそれとは異なるだけである。

今度は以下の様な対称T字回路について考えてみる。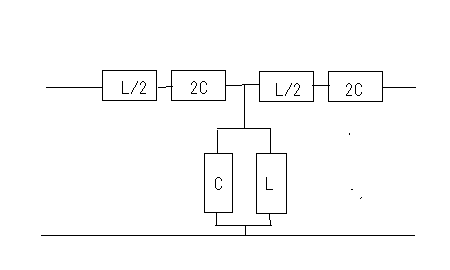



Z1,Z2およびパラメータxは

\begin{eqnarray}<br />Z_1&=&j\omega\frac{L}{2}+\frac{1}{j\omega 2 C}=j\frac{{\omega}^2 L C-1}{2\omega C}\\<br />Z_2&=&\frac{1}{j\omega C+\frac{1}{j\omega L}}=-j\frac{\omega L}{{\omega}^2 L C-1}\\<br />x&=&\sqrt{\frac{-Z_1}{4 Z_2}}=\sqrt{\frac{-j\frac{{\omega}^2 L C-1}{2\omega C}}{-4j\frac{\omega L}{{\omega}^2 L C-1}}}\\<br />&=&\left(\frac{\sqrt{L C}}{2}\right)\frac{{\omega}^2-\frac{1}{L C}}{\omega}<br />\end{eqnarray}

ということになる。定K形フィルタの条件を満足する対称T字回路なので映像インピーダンスの式は以前のものと変わらないが、パラメータxとωの写像関係が異なっている。xの零点が0ではなくZ1およびZ2の共振／反共振角周波数に移動している。極は0である点は変わっていない。これによって減衰定数と位相定数のプロットは、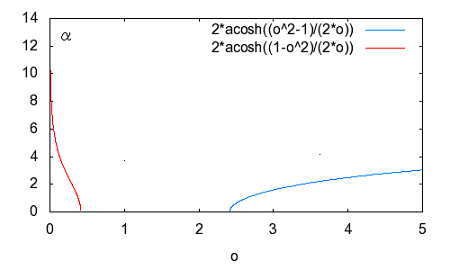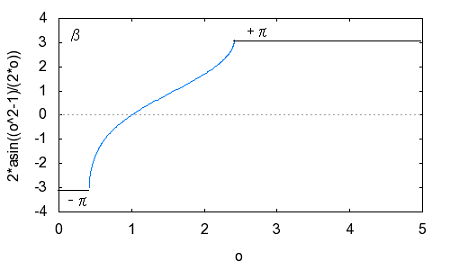




Valkenburgの描いたβのプロットはちょっと正確ではないことが実際に描いてみてわかった。通過域はあっているのだが、零点が2のすぐそばにあるように描かれてしまっているのだ。コンピュータの無い時代に書かれた本であるので、トレースでなぞった際にずれてしまったのかもしれない。写植字のミスという可能性もある。

いずれにせよこれは帯域通過フィルタであることを示している。ということはZ1とZ2を逆にすれば帯域除去フィルタになるのだろうか、どうやらそうらしい。それを確かめるのは読者の課題としよう（´∀｀　）

今日の電気回路理論の参考書で定K形フィルタの理論が紹介されているのはせいぜいあと誘導m形フィルタに触れる程度だ。実際にそれらのフィルタ回路の合成方法に関する議論はまったくと言っていいほど割愛されている。というのも合成に不可欠な一端子対回路について割愛していることが多いからだ。そこで学ぶFoster展開が合成の話をするには知っていることが前提となる。

Valkenburgは半世紀前の執筆当時は有益だったと思われる定K形フィルタ合成について引き続きたくさんのページを割いて説明している。貴重なのでここで紹介することにしよう。

ここまで登場した回路は単純なフィルタ特性のものばかりだったが、もし複数の異なる通過域や減衰域を持つフィルタを設計する場合にはどうすればよいだろう。定K形フィルタ回路のZ1,Z2が満足すべき条件式を以下の様に書き直すと

\begin{eqnarray}<br />Z_1&=&\frac{R^2}{Z_2}<br />\end{eqnarray}

1/Z2をアドミッタンスY2で置き換えると

\begin{eqnarray}<br />Z_1&=&R^2 Y_2<br />\end{eqnarray}

ここから以下の例の様に意図した零点と極を持つZ1が一端子対回路で学んだ第一Foster展開(部分分数展開）により、Y2が第二Foster展開で合成できる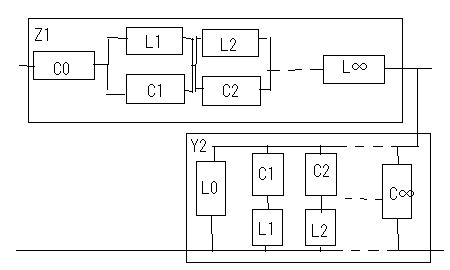

\begin{eqnarray}<br />Z_1&=&R^2\frac{\left(s^2+{s_1}^2\right)\dots}{s\left(s^2+{s_2}^2\right)\dots}\\<br />Y_2&=&\frac{\left(s^2+{s_1}^2\right)\dots}{s\left(s^2+{s_2}^2\right)\dots}<br />\end{eqnarray}



具体例を挙げればY2が

\begin{eqnarray}<br />Y\left(s\right)&=&\frac{\frac{2}{L_n}}{\left(s^2+\frac{1}{L_n C_n}\right)}<br />\end{eqnarray}

で表される場合、Z1はその逆回路となるので

\begin{eqnarray}<br />Z\left(s\right)&=&\frac{\frac{s}{C_m}}{\left(s^2+\frac{1}{L_m C_m}\right)}<br />\end{eqnarray}

ということになる。ここで定K形フィルタとなるにはCn,Ln,Cm,Lmの値は以下の条件を満たす関係を持つ必要がある

\begin{eqnarray}<br />Z\left(s\right)&=&R^2 Y\left(s\right)<br />\end{eqnarray}

一般形にすると

\begin{eqnarray}<br />\frac{N_1\left(s\right)}{\left(s^2+\frac{1}{L_m C_m}\right)\left(s^2+\frac{1}{L_{m+2}C_{m+2}}\right)\dots}&=&R^2\frac{N_2\left(s\right)}{\left(s^2+\frac{1}{L_n C_n}\right)\dots}<br />\end{eqnarray}

これが成り立つには、

\begin{eqnarray}<br />L_m C_m&=&L_n C_n=\frac{1}{{\omega_n}^2}\\<br />\frac{L_m}{L_n}&=&\frac{C_n}{C_m}<br />\end{eqnarray}

を満たす場合のみということになる。ここでValkenburgの著書に誤植を見つけた。Cn/CmであるべきがCn/Cnとなっていたのだ。

Foster展開の他にCauer展開（連分数展開）を使うことで同じ特性のフィルタを以下の様にラダー回路で構成することが可能である。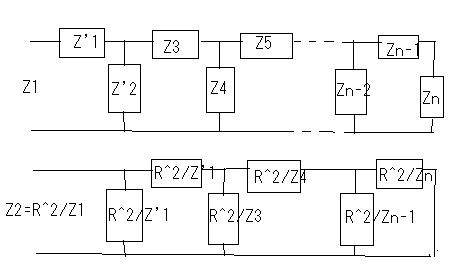



複合フィルタ(composite filter)

同一の映像インピーダンスを持つ定K形フィルタ（対称T字形、対称π形）を縦続接続して構成されるフィルタは複合フィルタ(composite filter)と呼ばれ、半世紀前には代表的なフィルタ回路構成法だった。映像インピーダンス整合がとれているため、n個の縦続接続された複合フィルタの減衰定数は総和となるため

\begin{eqnarray}<br />\alpha&=&2 n\,cosh^{-1}\,\frac{\omega}{\omega_0}<br />\end{eqnarray}

ということになる。nを変えてそれぞれをプロットすると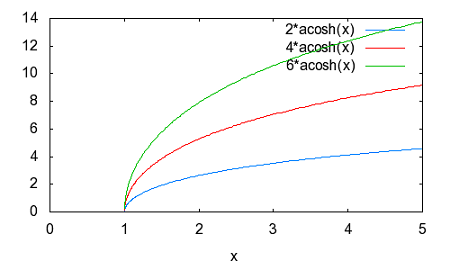



段数を増やすと減衰定数は増加する。しかし急峻な特性が要求される場合には、非常に多くの段数を必要とすることになる。

定K形複合フィルタの限界は

(1)遮断周波数付近の減衰域で高い減衰を要求される場合、多数のT字回路を必要とする。このことは複合フィルタのコストを高沸させることになる。
(2)複合回路網は必要とされる映像インピーダンスで終端することができない。実際にはそのような終端インピーダンスは現存しないからである。フィルターを定抵抗Rで終端するとある周波数を除くすべての周波数で不整合を招く。

これらの限界から、減衰域での高い減衰を得るためにZobelは1923年に次なる改良された誘導M形フィルタ(m-derived filter)を生み出した。

P.S

やはり二端子対回路で映像パラメータが線形代数の視点から見ると伝送行列の固有値と固有ベクトルだと気づいても、それを生み出した古典フィルタ理論をちゃんと研究しない限り、それは所詮表層的理解に過ぎないということを痛感した次第。特に映像インピーダンス関数や映像伝達関数をωを変数とする1変数関数としてだけではなく、αやβも変数として多変数関数としてその振る舞いを調べることは有用であり、それらの本質や物理的な意味を直感するには不可欠であるということを学ぶことができた。

学校ではカリキュラムが膨大化する中、これらの古典理論に関しては割愛されるに至って久しい。もはや教養としての工学を教えているだけと言ってもいいかもしれない。演習問題を多く解くことも必要だが、演習問題を解くだけでは独力では気づかない数学的な視点などは教わらない限り身につかないだろう。Valkenburgの著書にはそうした時代を経ても普遍の価値を持つことが書かれている。
フラット表示 前のトピック | 次のトピック

題名 投稿者 日時
   フィルタ webadm 2011-5-3 7:21
     概説 webadm 2011-5-4 9:24
   » 定K形フィルタ webadm 2011-5-24 5:11
     誘導M形フィルタ webadm 2011-6-1 5:49
     複合フィルタ(composite filter) webadm 2011-6-10 5:50
     抵抗減衰器 webadm 2011-7-18 1:22

投稿するにはまず登録を
 
ページ変換(Google Translation)
EQPlayers
Allakhazam
EQresource VoA Home
Googleish(EN)
Googlean(KO)
Googlchinese(ZH-CN)
Googltwinese(ZH-TW)
Googlussian(RU)
Googlench(FR)
Googlerman(DE)
Googlabic(AR)
Googlindi(HI)
Googluguese(PT)
Googlutch(NL)
Googltarian(IT)
Googlpanish(ES)
Googlinnish(FJ)
Googlwedish(SY)
Googlatian(HR)
Googlzech(CS)
Googlgarian(BG)
Googlpolish(PL)
Googlmanian(RO)
Googlwegian(NO)
Googleek(EL)
Googldanish(DA)
サイト内検索

高度な検索