| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2016-1-10 22:07 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3084 |
Re: 自分の数学を持つことの勧め さて内積と外積の定義に関する疑問から発した旅はまだ終わっていない。
双対基底の存在を知り、反変ベクトルと共変ベクトルの違いを理解した上で、内積と外積に関する更なる疑問が生じてきた。 ・一般の斜交基底での内積と外積は直交基底と定義を変える必要があるか? ・一般の斜交基底での反変ベクトル間の外積はやはり反変ベクトルか、また共変ベクトル間の外積はやはり共変ベクトルか? この疑問に関して検索して調べたところ結果は不毛に終わった。 内積で検索してもまるでみんな言い合わせたように正規直交基底を前提にした内積の定義を結果だけ示して終わっている。 手元の有名なベクトル解析の本やテンソル解析の本を見ても、この疑問には直接答えるような章や部分は見当たらない。 まるで世界中を敵まわすような疑問を抱いてしまったことを感じた。 世界を敵にまわしたと感じるのは小学生依頼久々である。 小学生の時は社会から追放されるという危機感を感じて自分の疑問そのものを封印してしまったが、それは間違いだったと今後悔している。世界を敵に回しても戦わなければならない時はあるのだ。 もちろん、敵の視点からすれば、ベクトルの成分によらない内積の定義は基底に依存しないので修正する必要がないと主張するだろう。それに関しては異論はない。 問題は上の定義に現れるベクトルの大きさ|a|,|b|は斜交基底の元ではどう表されるかである。 既に一般の基底を選んだ段階でベクトルの成分は反変成分となり、基底に依存して大きくもなり小さくもなる。 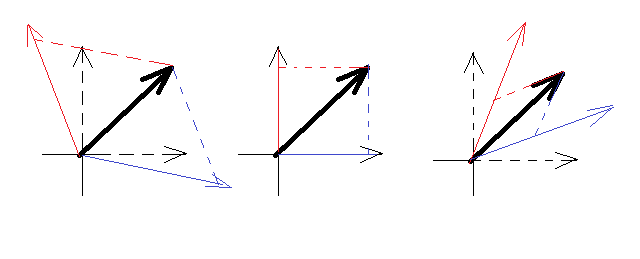 どうしてこのことに誰も口を開かないのだろう? 高校の数学で斜交座標系を教わるらしいが、これに関する議論は検索ではまったくひっかからない。高校には通ったことが無いので知らない。 更にひどいことに斜交基底の存在すら口にすることもはばかられることがあるのかどうか出てこない。 どうやら禁断の領域に足を踏み入れてしまったぽい。 どうも秘密にされていることがあるようなにおいがぷんぷんする。 秘密を嫌う者としてはこれは暴かねばならない。 検索すると結論だけ述べていてそれに至る過程については一切触れていない記事は見かける。 また同様の議論はEinsteinの相対性理論で結果だけ示されて世界が動揺したという歴史があるらしい。Einsteinの手書きのノートにも実のところ結論の式しか記されていないので、どうやってそれを見いだしたかは謎である。 なので普通は相対性理論とかそれに使われているRiemann幾何を学ぶ人しか知らなくていい領域なので高校や大学では絶対触れないという決まりのように想像される。違うだろうか? しかしもっと早く知っていれば、というか何故最初に内積の定義を教わった時に疑問を抱かなかったかということを後悔している。確かに正規直交基底を用いる限りにおいては簡単な定義で済んでしまうのでそれに甘んじていたというのがある。言い換えれば甘く見ていたと言える。 ここからはどこにも書かれていない(少なくとも検索した範囲では)斜交座標系に修正された内積の定義を導くことにする。 まずはベクトルの大きさ(ノルム:Norm)をどうやって計るかが問題である。 正規直交基底(e1,e2,e3)を用いてベクトルvは という線形結合で表されるのは言うまでもない。 またその場合、ベクトルの大きさ|v|とベクトルの成分の関係は となることはどのテキストにも書いてある。 もはや上の成分での定義は正規直交基底の特種性に依存し、斜交基底ではまったく成り立たないのは明らかである。 問題は基底を正規直交基底(e1,e2,e3)から斜交基底(f1,f2,f3)に変換した場合、ベクトルの大きさはどうなるかということである 従って元の正規直交基底でのベクトル成分は斜交基底でのベクトル成分を使って以下の様に表すことができる これを最初の正規直交基底でのベクトルのノルムの定義式に代入すると ということになる。 行列表現では 従って変換行列が恒等変換(単位行列)の場合には行列の対角成分T11,T22,T33が全て1で、それ以外は0であることから、正規直交基底でのベクトルのノルムの定義式と一致する。やはり正規直交基底は特種なケースだったわけだ。 ところで正規直交基底から斜交基底への変換行列とはいったいどんな成分から成るのだろうか? それは先に挙げた変換式からただちに なんと基底を順番に縦に並べた行列のことだった。 先の一般基底でのベクトルのノルムは という風に表すことができる。 このgijを成分とする行列は、計量(metirc)テンソル、基本計量テンソル、基本テンソル、Riemann計量とか様々の名前で呼ばれるものである。この二階のテンソルと2つのベクトルのテンソル積を二重に縮約すると0階のテンソル(スカラー)への線形写像となるわけである。 こんなに早くにお目にかかるとは光栄である。 すなわち正規直交基底では計量テンソルは単位行列になるため見えなくなってしまうが、一般の基底では正則な対称行列となる。 なんだそうだったのか(´∀` ) どうしてこんな大事なことを誰も書いてないのだろう、やっぱり世界を敵にまわしたかも。 この計量テンソルを使えば、意外に簡単に一般の基底へ内積の定義を得ることができそうな予感がする。 と思った瞬間に答えの一歩前まで来ていることに気付いた。片方を同じ基底に関する別の反変ベクトルに置き換えれば済む話だった。 計量テンソルが内積の定義に先だって存在しないといけないというのが判っただけでも大変な収穫であるが、それだけではない。 大抵のRiemann幾何のテキストには上の結果が天下り的に示されているだけである。大学院に入って初めて計量テンソル、もしくは基本計量テンソル、基本テンソル、Riemann計量、に出くわすのでは遅すぎる感がする。もっと早くに出来れば最初から一般の座標系で早い時点で計量テンソルの重要性を認識していれば、「あ計量テンソルですね、わかります」で済んでしまう話である。 最初に極めて特種なケースである正規直交系で一般性を失った形で教え込まれてしまうと後で取り返しのつかないことになる。テキストによっては、可能な限り一般性を失わない形で正規直交系でベクトル解析を構築しているものもある。それは一般の基底のベクトル解析(多様体上の解析)を学んだ後でやっとその違いが判る。そこまで配慮して書かれたテキストは少ない。 さて収穫はそれだけではない。一般の座標系で内積の定義は上の形だけだろうか? 上の定義では反変ベクトルと共変テンソルの組み合わせだが、それ以外に組み合わせがあるはずである。 実際には4通りの組み合わせがあるが、そのうち2つは前後が逆なだけで同値である。内積は可換な作用なので前後入れ替えても結果は同じである。そうすると残る2種類はどんな形だろう? 実は先の結果からは直感的にはおよそ思いつかない驚愕の事実が判明することになる。たまたま偶然に再発見した。 先の内積の定義を自然基底(f1,f2,f3)に関する反変ベクトル成分だけでなく、双対基底に関する共変ベクトルも併用してみたらどうなるだろうか? 共変ベクトルの成分は基底変換と同じ変換を受けるから (2016/7/14)訂正 従って (2016/7/14)訂正 という関係が成り立つ。 これを一般のベクトルのノルムの式の片方に代入すると なんと成分だけの式になってしまった。本当は計量テンソルが単位行列の形をしているだけなんだけどね。 先の結果と合わせると つまり計量テンソルにはベクトルに作用すると反変から共変へ、共変から反変へ変換する機能があるという事実が判明したことになる。これは直感では絶対わからない(天才でもないかぎり)。苦労してへたくそな行列計算を積み重ねるとIQが低くてもこの事実に辿りつくことができる。やっぱり線形代数は身につけておくべきツールだということを痛感。 Riemann幾何や物理学とかではもうこのことは常識として扱われていて、「添え字の上げ下げ」を行う機能として頻繁に登場する。内積を定義するだけではなかったのね。「計量テンソル」で検索してもほとんどまともな記事は出てこないけど、「添え字の上げ下げ」で検索すると計量テンソルのことが山ほど出てくるというのは笑える(´∀` ) 同様に今度は上の結果を利用してもう片方の反変ベクトルを共変ベクトルに変えてしまう(添え字を下げる)と ということになる。 最後のは計量テンソルの成分の添え字が二つとも上付きになっている点に注意。反変テンソルである。 とどのつまり計量テンソルには以下の4種類あることになる 共変テンソル(添え字が下のみ)、2つの混合テンソル(添え字が上と下両方混在)、それに反変テンソル(添え字が上のみ)の4種であるが、混合テンソルはいずれも単位行列なので他と違って添え字の上げ下げの機能は持たず無害、共変テンソルと反変テンソルは互いに逆の作用を持つ関係にある。 これだけの事実を再発見できたことは収穫である。テキストでは当たり前の事実として当たり前のように頻繁に利用されるので大学院になってから知らないでは済まされない。今のうちに自分で発見して判ってしまえば怖いものはない。 テキストでは添え字記法を使って上の結果を天下り的に示しているものがほとんどであるが、基本的な線形代数の基礎知識と行列計算方法を知っていれば下手な計算でも結果を導出できることを示せたことはうれしい。今日はぐっすり眠れそうである(´∀` ) P.S この段階で得られた成果ですっかり舞い上がってしまってもうひとつの設問を忘れていることに気付いた。 ベクトルの外積は一般の基底ではどうなるのだろうかという点である。これについては新たな記事で議論することにしよう。 P.S 後で読み返したら、内積の混合形式の導出に欠陥があったので、欠陥の無いものに差し替えたのは内緒だ。 P.S カタカナで(ノルム)と括弧内に書くと一瞬顔文字に見えたりするのは私だけだろうか? きっと疲れているんだ。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| » |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

