Gan's blog - フォーラム

(1) 2 3 4 ... 7 »

投稿者	スレッド
webadm	投稿日時: 2010-5-20 4:53
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	2端子対回路演習問題本書の特徴として理論は概説にとどめて各論は演習問題でというスタイル。実際その方が身をもって学ぶというか、自分で調べたり考えたりしないといけないので良い感じ。下巻の内容はどれもまだ生きている分野の入口を紹介しているだけなので、本格的に深く学ぼうとすると他の専門書に頼るしかない。それでも現代でも解決を待たれている問題や課題は歴史を辿ることでしか知るすべが無い。電気工学ポケットブックや電子工学ハンドブック、電子回路集とか見てもすでに解決された答えしか載っておらず、それすらそれらの答えに辿りついた経緯や手法は明かされていない。これは数学の世界も同じで。Gaussに限らず数学者は誰も「足場は残さない」というスタイルに徹していて、証明方法を除いてはそれに居たる経緯は口外しないものだ。唯一死後に日記や研究メモとかが明らかにされることでその一端をのぞき見ることができるにすぎない。実務で回路設計に携わると自分で答えを導くよりも、誰かが既に同じ問題を解いていたらそれを使いたいという誘惑にかられる。当然そうした実務者向けにハンドブックやら便覧やらが出版されているものの、それらにずばり載ってなければやはり自分で解くしかないことになる。実務向けのそうしたハンドブックは意外にも理論的なことにはページを割いておらず、結論だけを集めたという感じのものがほとんど。いざ理論からしっかりやろうとすると、大学の教科書や参考書が一番まとまっているというのが現状。もともと限られた時限で広範囲に基礎を理解させるという目的で書かれているので当然である。しかし基礎だけでは現実の問題を解くにはギャップがありすぎて、やはりその先は専門領域の各論にスポットライトを当てた専門書や論文から学ぶしかない。中には目的をもたない理論研究というのもあって、数学もそうだけど目的を持たないから、あらゆる問題に応用できるという面がある。特定の目的のために考えられた手法は意外に適用範囲が狭いものである。手法を考える場合にどうしても前提条件を多くして適用範囲を狭めることになりがちであるが、一方で目的を忘れて、もっと広範囲に一般化して考えることによって寿命の長い理論が見えてくる場合がある。実務の現場では前者で十分だし、それ以上欲張ると時間とお金の制約から無理であるが、一端喉元を過ぎた後にゆっくり同じ問題や類似のもっとバリエーションの異なる問題の可能性を考えることによって一般的な解法が見つかることもある。それには抽象数学の考えかたや問題の対象のとらえ方に参考になるものがある。それらは特定の目的をもっていないので、なんにでも応用が利くという最大の利点を持つ。話しが長くなったが演習問題を解いていこう。

webadm	投稿日時: 2010-5-20 5:54
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	インピーダンスパラメータ &&線形受動素子のみで構成される任意の二端子対回路で一次側と二次側の電圧、電流の関係は４つのインピーダンスパラメータz11,z12,z21,z22で表すことができることを示せという問題。基本的なことだが、実は良く解っていなかったりする。一端子対回路の時のように一般的な電源を含まないn端子対線形受動回路網の２端子対を除いてすべて短絡したものが二端子対回路 n端子対回路のインピーダンス行列と各端子対の電圧と電流の関係を行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />E_2\\<br />0\\<br />\vdots\\<br />0<br />\end{array}\right]&=&\left[\begin{array}<br />Z_{11} & Z_{12} & Z_{13} & \cdots & Z_{1n}\\<br />Z_{21} & Z_{22} & Z_{23} & \cdots & Z_{2n}\\<br />Z_{31} & Z_{32} & Z_{33} & \cdots & Z_{3n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots\\<br />Z_{n1} & Z_{n2} & Z_{n3} & \cdots & Z_{nn}<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2\\<br />I_3\\<br />\vdots\\<br />I_n<br />\end{array}\right]<br />\end{eqnarray}$ 証明のストラテジーとしては、I3～Inと無関係にE1,E2,I1,I2とインピーダンス行列の関係式を導けば良いことになる。どうすんだこれ（；´Д｀）著者の解答や他の参考書「電気回路の基礎」足立修一、森大毅共著　東京電機大学出版局をちらりと覗き見するといずれも共通して分割行列表現を使用してI3～Inをうまい具合に消去している。偶然消去されるというのではストラテジーがなさすぎる。意地を張って別解を考えようとすると今の季節、眠くなってすぐに寝てしまう。横になりながら考えていると、謎の定理の文章が目の前を流れていき、つかもうとしても捕まえられないというもどかしさ。記憶に残すこともできず。とりあえずE1,E2,...,Enの単位が電圧であるとか、I1,I2,...,Inの単位が電流であるとかを一旦忘れてn次元空間の一点を表す座標と考えるとそれぞれQ(E1,E2,...,En),P(I1,I2,...,In)と表すことができる。それと原点O(0,0,...,0)とを結ぶ直線がただ一つ決まるとするとそれはn次元空間上のベクトルOQ,OPとみなすことができる。ベクトルOQがベクトルOPの間にはAなる線形変換(原点を中心とする回転と拡大縮小のスケーリング）が唯一存在することになる。それらのn次元の点を二次元平面に投射した場合、原点OはO'に点P,Qは点P',Q'にそれぞれ投射されることになる。同様に二次元平面上のベクトルO'P'とO'Q'の間にも線形変換A'が唯一存在することになるが、その場合AとA'の間にどういう関係が成り立つかという問題に帰着する。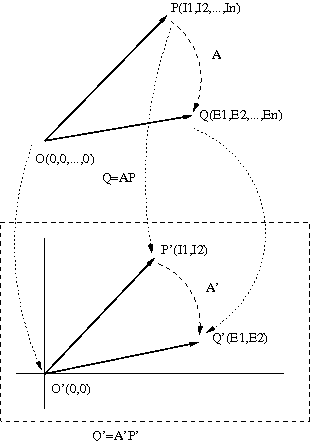益々わからなくなってきた。よくCGやゲームで三次元オブジェクトを二次元ディスプレイ空間にレンダリングする際もこれと同じである。古くは影絵とかの伝統芸能もこうした理論が背後にある。宮本武蔵が小次郎に勝った時も船の舵で作った通常より長い木刀を小次郎の目の網膜上の二次元に投射された際に長さが実際よりも短く錯覚するような線形変換テクニックを駆使したと思われる。よく考えたらわざわざ誰もこんな難しいこと考えないので、検索してもヒントはみつからない。意外にコンピュータグラフィックスの数理は知られていないものだということを知る。昔勉強した時に学んだ式すらどこにも見あたらない。しかしそれも必要無いということがようやくわかった。基本的に上の二端子対回路のモデルではI3～Inは独立ではなくI1,I2に依存するので、E1,E2,I1,I2とインピーダンスマトリックスの関係のみ考えればよく $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12} & Z_{13} & \cdots & Z_{1n}\\<br />Z_{21} & Z_{22} & Z_{23} & \cdots & Z_{2n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots\\<br />Z_{n1} & Z_{n2} & Z_{n3} & \cdots & Z_{nn}<br />\end{array}\right]^{-1}\left[\begin{array}<br />E_1\\<br />E_2\\<br />0\\<br />\vdots\\<br />0<br />\end{array}\right]&=&\left[\begin{array}<br />I_1\\<br />I_2\\<br />\vdots\\<br />I_n<br />\end{array}\right]\\<br />\frac{1}{\Delta}\left[\begin{array}<br />\Delta_{11} & \Delta_{12} & \Delta_{13} & \cdots & \Delta_{1n}\\<br />\Delta_{21} & \Delta_{22} & \Delta_{23} & \cdots & \Delta_{2n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots\\<br />\Delta_{n1} & \Delta_{n2} & \Delta_{n3} & \cdots & \Delta_{nn}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2\\<br />0\\<br />\vdots\\<br />0<br />\end{array}\right]&=&\left[\begin{array}<br />I_1\\<br />I_2\\<br />\vdots\\<br />I_n<br />\end{array}\right]\\<br />\left[\begin{array}<br />\frac{\Delta_{11}}{\Delta} & \frac{\Delta_{12}}{\Delta}\\<br />\frac{\Delta_{21}}{\Delta} & \frac{\Delta_{22}}{\Delta}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]^{-1}\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\frac{1}{y_{11}y_{22}-y_{12}y_{21}}\left[\begin{array}<br />y_{22} & -y_{12}\\<br />-y_{21} & y_{11}<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]\\<br />y_{ij}&=&\frac{\Delta_{ij}}{\Delta}\\<br />\end{eqnarray}$ ということになる。ここでΔはインピーダンス行列の行列式、Δijはインピーダンス行列の余因子行列式である。 $\begin{eqnarray}<br />\Delta&=&\left\|\begin{array}<br />Z_{11} & Z_{12} & Z_{13} & \cdots & Z_{1n}\\<br />Z_{21} & Z_{22} & Z_{23} & \cdots & Z_{2n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots\\<br />Z_{n1} & Z_{n2} & Z_{n3} & \cdots & Z_{nn}<br />\end{array}\right\|\\<br />\Delta_{ij}&=&\left(-1\right)^{i+j}\left\|\begin{array}<br />Z_{11} & Z_{12} & Z_{13} & \cdots & Z_{1 \left(j-1\right)} & Z_{1 \left(j+1\right)} & \cdots & Z_{1n}\\<br />Z_{21} & Z_{22} & Z_{23} & \cdots & Z_{2 \left(j-1\right)} & Z_{2 \left(j+1\right)} & \cdots & Z_{2n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\<br />Z_{\left(i-1\right) 1} & Z_{\left(i-1\right) 2} & Z_{\left(i-1\right) 3} & \cdots & Z_{\left(i-1\right)\left(j-1\right)} & Z_{\left(i-1\right)\left(j+1\right)} & \cdots & Z_{\left(i-1\right) n}\\<br />Z_{\left(i+1\right) 1} & Z_{\left(i+1\right) 2} & Z_{\left(i+1\right) 3} & \cdots & Z_{\left(i+1\right)\left(j-1\right)} & Z_{\left(i+1\right)\left(j+1\right)} & \cdots & Z_{\left(i+1\right) n}\\<br />\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\<br />Z_{n1} & Z_{n2} & Z_{n3} & \cdots Z_{n\left(j-1\right)} & Z_{n\left(j+1\right)} & \cdots & Z_{nn}<br />\end{array}\right\|<br />\end{eqnarray}$ 実際に上記の式に基づいてn=3やn=4のケースで計算してみると著者の方法によるものと同じ結果が得られる。 n=3のケースでは $\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]=\left[\begin{array}<br />\frac{Z_{11}\,Z_{33}-Z_{13}\,Z_{31}}{Z_{33}} & \frac{Z_{12}\,Z_{33}-Z_{13}\,Z_{32}}{Z_{33}}\\<br />\frac{Z_{21}\,Z_{33}-Z_{23}\,Z_{31}}{Z_{33}} & \frac{Z_{22}\,Z_{33}-Z_{23}\,Z_{32}}{Z_{33}}<br />\end{array}\right]$ n=4のケースでは $\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]=\left[\begin{array}<br />\frac{Z_{11}\,Z_{33}\,Z_{44}-Z_{13}\,Z_{31}\,Z_{44}-Z_{11}\,Z_{34}\,Z_{43}+Z_{14}\,Z_{31}\,Z_{43}+Z_{13}\,Z_{34}\,Z_{41}-Z_{14}\,Z_{33}\,Z_{41}}{Z_{33}\,Z_{44}-Z_{34}\,Z_{43}} & \frac{Z_{12}\,Z_{33}\,Z_{44}-Z_{13}\,Z_{32}\,Z_{44}-Z_{12}\,Z_{34}\,Z_{43}+Z_{14}\,Z_{32}\,Z_{43}+Z_{13}\,Z_{34}\,Z_{42}-Z_{14}\,Z_{33}\,Z_{42}}{Z_{33}\,Z_{44}-Z_{34}\,Z_{43}}\\<br />\frac{Z_{21}\,Z_{33}\,Z_{44}-Z_{23}\,Z_{31}\,Z_{44}-Z_{21}\,Z_{34}\,Z_{43}+Z_{24}\,Z_{31}\,Z_{43}+Z_{23}\,Z_{34}\,Z_{41}-Z_{24}\,Z_{33}\,Z_{41}}{Z_{33}\,Z_{44}-Z_{34}\,Z_{43}} & \frac{Z_{22}\,Z_{33}\,Z_{44}-Z_{23}\,Z_{32}\,Z_{44}-Z_{22}\,Z_{34}\,Z_{43}+Z_{24}\,Z_{32}\,Z_{43}+Z_{23}\,Z_{34}\,Z_{42}-Z_{24}\,Z_{33}\,Z_{42}}{Z_{33}\,Z_{44}-Z_{34}\,Z_{43}}<br />\end{array}\right]$ ということになる。なんとなく暗号処理みたいに複雑で元の回路のインピーダンスマトリックス要素が配合されている。まんざら暗号処理と関係なくもなさそうである。暗号文と平文は互いに代数的な操作によって相互に変換可能である。こんなことは理数系から見ると当たり前で「ばーか、ばーか」と工学系が馬鹿にされる格好の材料でもある。これだから工学系は理数系に一生頭が上がらないのかもしれない。 P.S ううむ危うく神経衰弱になって三日三晩寝込むはめになるところだった。いきなり大きい絵を描くのは身の程知らずだったということ。それ以前に逆行列について良くわかってなかったことも判明したり。線形代数も今の時代色々本が出ているけど、どれもまとめに徹していて他の数学の分野とのリンクとか全然触れてないし、歴史的経緯すら触れてない。ファイナンス数理で線形代数が必須とかで売れているのかもしれない。そんなこと数学者もまったく予想してなかっただろうね。元々純粋数学だった確率微分方程式も金融工学でデリバティプ商品の値付け理論に使われてから急にスポットライトを浴びたようなものだし。結局一番解りやすかったのは戦前のまだ線形代数とか無かった時代の高木貞治の「代数学講義」の行列と行列式の章だった。歴史的経緯からはじまるし、昔の文体は外来語がひらがなで本文は旧漢字カタカナでなかなか味わいがあってじっくり読めた（というか速読できないしこれ）。寺澤寛一の「自然科学者のための数学概論」は行間隔や文字の大きさのバランスが絶妙にすばらしく、美しく読みやすい本であるが線形代数はおろか代数系の話しがまったくない古典解析の本でもある。それでも行列表記は随所のページに登場するが、行列そのものの理論は扱っていない。もちろん集合とかもブルバキ以前なので出てこない。行列の概念は非常にマイナーだったし、便利なのでいろいろ少しずつ多くの数学者に使われるようになって、蟻の巣穴のようにあちこちの分野とつながりだしてから、まとめて教えるということになったのだろう。しかしつながってる先を学ぶのが本来の意図なのだろうけど、数学は意図も目的も無いので無味乾燥なものとなるのは仕方がない。いきなり最初の問題で読者の出端をくじくのが本書の常套手段だ。

webadm	投稿日時: 2010-5-22 23:43
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	インピーダンスパラメータとアドミッタンスパラメータ次ぎの問題は、前問の解で既に出てきてしまったが、インピーダンスパラメータとアドミッタンスパラメータの変換式を導けというもの。インピーダンスパラメータ（Ｚ行列）とアドミッタンスパラメータ（Ｙ行列）は互いに逆行列な関係にあるので $\begin{eqnarray}<br />\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]^{-1}=\frac{1}{y_{11}y_{22}-y_{12}y_{21}}\left[\begin{array}<br />y_{22} & -y_{12}\\<br />-y_{21} & y_{11}<br />\end{array}\right]\\<br />\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]^{-1}=\frac{1}{z_{11}z_{22}-z_{12}z_{21}}\left[\begin{array}<br />z_{22} & -z_{12}\\<br />-z_{21} & z_{11}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。代数的にはインピーダンスパラメータとアドミッタンスパラメータは互いに他方の逆元で、唯一つ存在することになる。このような線形変換行列は並行移動要素も含むAffine変換群に包含される。

webadm	投稿日時: 2010-5-23 1:32
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	インピーダンスパラメータとハイブリッドパラメータ次ぎの問題はインピーダンスパラメータ(Z行列）とハイブリッドパラメータ(H行列）の間の変換を示せというもの。 Z行列はI1,I2とE1,E2の線形変換を表すが、H行列はI1,E2とE1,I2の間の線形変換である。変換する二点の座標を交換したようなものであるが、そういうふうに難しく考えると熱が出てくる。物事を難しく考えるのも才能の一つだと思って気を休めることにしよう。著者の解法も他の古い参考書にある通りの方法で当たり前すぎるので、もっと見通しの良い別解を考えてみよう。図のP,Q,P',Q'に関して以下の関係が成り立つ $\begin{eqnarray}<br />P&=&\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]Q^{\'}\\<br />Q&=&\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q^{\'}\\<br />P^{\'}&=&\left[\begin{array}<br />I_1\\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]Q\\<br />Q^{\'}&=&\left[\begin{array}<br />E_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]P+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q<br />\end{eqnarray}$ Z行列表記にそれぞれ代入して整理すると $\begin{eqnarray}<br />Q=Z P=\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]\left(\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]Q^{\'}\right)&=&\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q^{\'}\\<br />\left(\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]-\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\right)Q^{\'}&=&\left(\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]-\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\right)P^{\'}\\<br />\left[\begin{array}<br />-1 & z_{12}\\<br />0 & z_{22}<br />\end{array}\right]Q^{\'}&=&\left[\begin{array}<br />-z_{11} & 0\\<br />-z_{21} & 1<br />\end{array}\right]P^{\'}<br />\end{eqnarray}$ 更に左辺の係数行列の逆行列を両辺に乗じると $\begin{eqnarray}<br />Q^{\'}&=&\left[\begin{array}<br />-1 & z_{12}\\<br />0 & z_{22}<br />\end{array}\right]^{-1}\left[\begin{array}<br />-z_{11} & 0\\<br />-z_{21} & 1<br />\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}<br />-1 & \frac{z12}{z22}\\<br />0 & \frac{1}{z22}<br />\end{array}\right]\left[\begin{array}<br />-z_{11} & 0\\<br />-z_{21} & 1<br />\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}<br />z_{11}-\frac{z_{12}\,z_{21}}{z_{22}} & \frac{z_{12}}{z_{22}}\\<br />-\frac{z_{21}}{z_{22}} & \frac{1}{z_{22}}<br />\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}<br />\frac{z_{11}\,z_{22}-z_{12}\,z_{21}}{z_{22}} & \frac{z_{12}}{z_{22}}\\<br />-\frac{z_{21}}{z_{22}} & \frac{1}{z_{22}}<br />\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}<br />h_{11} & h_{12}\\<br />h_{21} & h_{22}<br />\end{array}\right]P^{\'}\\<br />\end{eqnarray}$ ちゃんとできたじゃないか(´∀` ) 同様に逆方向の変換は H行列表記にそれぞれ代入すると $\begin{eqnarray}<br />Q^{\'}&=&H P^{'}=\left[\begin{array}<br />h_{11} & h_{12}\\<br />h_{21} & h_{22}<br />\end{array}\right]\left(\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P+\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]Q\right)=\left[\begin{array}<br />0 & 0\\<br />0 & 1<br />\end{array}\right]P+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q<br />\end{eqnarray}$ これは先のZ行列の場合のP',Q'をP,Qにz11,z12,z21,z22をh11,h12,h21,h22に置き換わったものであるため、結果も同様に置き換えれば $\begin{eqnarray}<br />Q&=&\left[\begin{array}<br />\frac{h_{11}\,h_{22}-h_{12}\,h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}}\\<br />-\frac{h_{21}}{h_{22}} & \frac{1}{h_{22}}<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />z_{11} & z_{12}\\<br />z_{21} & z_{22}<br />\end{array}\right]P\\<br />\end{eqnarray}$ ということになる。 P.S これらが線形代数ではどういう扱いになるのか知らない。読者の課題としよう(´∀` )

webadm	投稿日時: 2010-5-23 10:12
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	インピーダンス行列とアドミッタンス行列次ぎは以下に示す回路のインピーダンス行列とアドミッタンス行列を求めよという問題。２つの端子対は内部でストレートで結ばれていてインピーダンスZだけのshunt回路。端子対に流れる電流I1,I2はそれぞれ独立で、端子対の電圧E1,E2は常に同一でI1,I2とZによって以下の通り定まる $\begin{eqnarray}<br />E_1&=Z I_1+Z I_2\\<br />E_2&=Z I_1+Z I_2<br />\end{eqnarray}$ 従ってインピーダンス行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />Z & Z\\<br />Z & Z<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。アドミッタンス行列はインピーダンスの逆行列なので、それで求めようとすると、この回路のインピーダンス行列は行列式の値が0となってしまうので逆行列が存在しない。というのも先に書いた通りに、E1,E2は独立な値は取り得ない（端子同士が内部で直結しているので常に同じ電圧しか取り得ない）ためだ。敢えて関係式を書くとすると $\begin{eqnarray}<br />I_1&=Y E_1=Y E_2\\<br />I_2&=Z E_2=Y E_1<br />\end{eqnarray}$ 強いて行列表現すれば $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />Y & 0\\<br />Y & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]=\left[\begin{array}<br />0 & Y\\<br />0 & Y<br />\end{array}\right]<br />\end{eqnarray}$ しかしこれも逆行列は存在しない。以下の表現は一見すると逆行列を持ちそうにみえるが $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />Y & 0\\<br />0 & Y<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]<br />\end{eqnarray}$ しかしこの逆行列は先に導いたインピーダンス行列とは異なる。従ってこの回路にはインピーダンス行列と等価なアドミッタンス行列は存在しないということになる。次ぎは端子対間の一方にインピーダンスZが直列に挿入されている回路。一つの閉ループしか存在しないのでI1,I2が一次独立では無い時点で破綻している。ちょうど前の設問の逆である。一方アドミッタンス行列としてはE1,E2は独立なので重ね合わせの理で $\begin{eqnarray}<br />I_1&=\frac{1}{Z} E_1-\frac{1}{Z} E_2\\<br />I_2&=-\frac{1}{Z} E_1+\frac{1}{Z} E_2<br />\end{eqnarray}$ という関係が成り立ち、行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{Z} & -\frac{1}{Z}\\<br />-\frac{1}{Z} & \frac{1}{Z}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。これも逆行列は存在しない。最後の回路はE1,E2,I1,I2とも独立だが、E1,I1とE2,I2の間にまったく線形的な結合が無い。従って $\begin{eqnarray}<br />I_1&=Z_1 E_1\\<br />I_2&=Z_2 E_2<br />\end{eqnarray}$ という関係が成り立ち、インピーダンス行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1 & 0\\<br />0 & Z_2<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。これは逆行列であるアドミッタンス行列が存在し $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1 & 0\\<br />0 & Z_2<br />\end{array}\right]^{-1}\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />&=&\frac{1}{Z_1 Z_2}\left[\begin{array}<br />Z_2 & 0\\<br />0 & Z_1<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{1}{Z_1} & 0\\<br />0 & \frac{1}{Z_2}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-23 16:25
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	T形回路次ぎは少し複雑だが基本的なT形回路のインピーダンス行列とアドミッタンス行列を求める問題。重ね合わせの理で回路方程式をたてると $\begin{eqnarray}<br />E_1&=&\left(Z_1+Z_2\right)I_1+Z_2 I_2\\<br />E_2&=&Z_2 I_1+\left(Z_2+Z_3\right)I_2<br />\end{eqnarray}$ 従ってインピーダンス行列で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。これには逆行列があり、アドミッタンス行列は $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]^{-1}\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />&=&\frac{1}{\left(Z_1+Z_2\right)\left(Z_2+Z_3\right)-{Z_2}^2}\left[\begin{array}<br />Z_2+Z_3 & -Z_2\\<br />-Z_2 & Z_1+Z_2<br />\end{array}\right]^{-1}\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{Z_2+Z_3}{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3} & -\frac{Z_2}{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}\\<br />-\frac{Z_2}{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3} & \frac{Z_1+Z_2}{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}<br />\end{array}\right]^{-1}\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-23 16:33
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	続：T形回路次ぎは前問の応用問題。と書いてしまうとネタバレなのだが、もともとそうなのだから良しとしよう。以下の回路のインピーダンスパラメータを求めよというもの。まともに回路解析すると大変だが、よく見ると前問のT形回路とZ1,Z2,Z3をそれぞれ以下の様に置けば等価である。 $\begin{eqnarray}<br />Z_1(s)&=&R_1+L_1 s\\<br />Z_2(s)&=&\frac{1}{\frac{1}{L_2 s}+C_2 s}=\frac{L_2 s}{1+L_2 C_2 s^2}\\<br />Z_3(s)&=&\frac{1}{\frac{1}{R_3}+C_3 s}=\frac{R_3}{1+R_3 C_3 s}\\<br />Z_1(j\omega)&=&R_1+j\omega L_1\\<br />Z_2(j\omega)&=&\frac{j\omega L_2}{1-{\omega}^2L_2 C_2}\\<br />Z_3(j\omega)&=&\frac{R_3}{1+j\omega R_3 C_3}=\frac{R_3-j\omega {R_3}^2 C_3}{1+{\omega}^2 {R_3}^2 {C_3}^2}<br />\end{eqnarray}$ 従ってインピーダンスパラメータは $\begin{eqnarray}<br />\left[\begin{array}<br />Z_2+Z3 & Z_2\\<br />Z_2 & Z_1+Z_2<br />\end{array}\right]&=&\left[\begin{array}<br />R_1+j\omega L_1+\frac{j\omega L_2}{1-{\omega}^2L_2 C_2} & \frac{j\omega L_2}{1-{\omega}^2L_2 C_2}\\<br />\frac{j\omega L_2}{1-{\omega}^2L_2 C_2} & \frac{j\omega L_2}{1-{\omega}^2L_2 C_2}+\frac{R_3-j\omega {R_3}^2 C_3}{1+{\omega}^2 {R_3}^2 {C_3}^2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />R_1+j\omega\left(L_1+\frac{L_2}{1-{\omega}^2L_2 C_2}\right) & \frac{j\omega L_2}{1-{\omega}^2L_2 C_2}\\<br />\frac{j\omega L_2}{1-{\omega}^2L_2 C_2} & \frac{R_3}{1+{\omega}^2 {R_3}^2 {C_3}^2}+j\omega\left(\frac{L_2}{1-{\omega}^2L_2 C_2}-\frac{{R_3}^2 C_3}{1+{\omega}^2 {R_3}^2 {C_3}^2}\right)<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-23 17:20
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	π形回路次ぎは基本のπ形回路のアドミッタンスパラメータを求める問題。ストラテジーとして前の問題で出てきたような以下の２つの二端子対回路が並列接続されたものと等価であると考えるこの回路のアドミッタンスパラメータは以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />y^{\'}_{11} & y^{\'}_{12}\\<br />y^{\'}_{21} & y^{\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{Z_2} & -\frac{1}{Z_2}\\<br />-\frac{1}{Z_2} & \frac{1}{Z_2}<br />\end{array}\right]<br />\end{eqnarray}$ これも以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />y^{\'\'}_{11} & y^{\'\'}_{12}\\<br />y^{\'\'}_{21} & y^{\'\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{Z_1} & 0\\<br />0 & \frac{1}{Z_3}<br />\end{array}\right]<br />\end{eqnarray}$ 従って上記２つの二端子対回路を並列接続した時のアドミッタンス行列は $\begin{eqnarray}<br />\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />y^{\'}_{11} & y^{\'}_{12}\\<br />y^{\'}_{21} & y^{\'}_{22}<br />\end{array}\right]+\left[\begin{array}<br />y^{\'\'}_{11} & y^{\'\'}_{12}\\<br />y^{\'\'}_{21} & y^{\'\'}_{22}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{1}{Z_2} & -\frac{1}{Z_2}\\<br />-\frac{1}{Z_2} & \frac{1}{Z_2}<br />\end{array}\right]+\left[\begin{array}<br />\frac{1}{Z_1} & 0\\<br />0 & \frac{1}{Z_3}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{1}{Z_2}+\frac{1}{Z_1} & -\frac{1}{Z_2}\\<br />-\frac{1}{Z_2} & \frac{1}{Z_2}+\frac{1}{Z_3}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。なんだ簡単じゃないか(´∀` )

webadm	投稿日時: 2010-5-23 17:58
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	Zobel変換次ぎの問題は今まで登場してきたT形回路とπ形回路をそれぞれ等価変換(Zobel変換）する問題。ただしL1C1=L2C3が成り立つものとする。これも以前の問題の結果を利用して著者とは別解でやってみよう。最初に見通しがよくなるようにT形回路とπ形回路を以下のように表す。 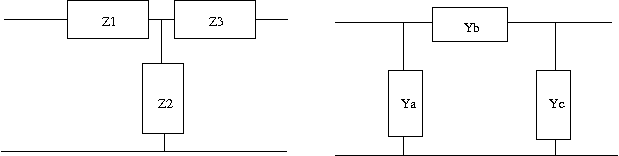T形回路のインピーダンス行列は以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]<br />\end{eqnarray}$ 同様にπ形回路のアドミッタンス行列も以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_a+Y_b & -Y_b\\<br />-Y_b & Y_b+Y_c<br />\end{array}\right]<br />\end{eqnarray}$ 一方各回路をそれぞれのパラメータで表すと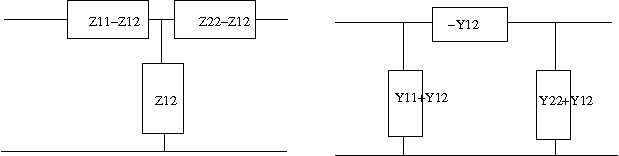次にT形回路のアドミッタンス行列をZ1,Z2,Z3で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />\frac{Z_2+Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3} & -\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />-\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3} & \frac{Z_1+Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}<br />\end{array}\right]<br />\end{eqnarray}$ 従ってπ形回路のYa,Yb,Ycを等価なT形回路のZ1,Z2,Z3で表すと $\begin{eqnarray}<br />Y_a&=&Y_{11}+Y_{12}\\<br />&=&\frac{Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />Y_b&=&-Y_{12}\\<br />&=&\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />Y_c&=&Y_{22}+Y_{12}\\<br />&=&\frac{Z_1}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}<br />\end{eqnarray}$ ここで題意よりT形回路のZ1,Z2,Z3は $\begin{eqnarray}<br />Z_1&=&\frac{1}{j\omega C_1+\frac{1}{j\omega L_1}}\\<br />&=&\frac{j\omega L_1}{1-{\omega}^2 L_1 C_1}\\<br />Z_2&=&j\omega L_2\\<br />Z_3&=&\frac{1}{j\omega C_3}\\<br />&=&-\frac{j}{\omega C_3}<br />\end{eqnarray}$ これを先のYa,Yb,Ycの式にそれぞれ代入するとL1C1=L2C3が成り立つ場合 $\begin{eqnarray}<br />Y_a&=&\frac{Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&-\frac{j}{\omega C_3\left(-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}\right)}\\<br />&=&-\frac{j\cancel{\left({\omega}^2L_1 C_1-1\right)}}{\omega\left(L_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+L_2\cancel{\left({\omega}^2L_1 C_1-1\right)}\right)}\\<br />&=&-\frac{j}{\omega\left(L_1+L_2\right)}\\<br />Y_b&=&\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&\frac{j\omega L_2}{-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}}\\<br />&=&\frac{j\omega L_2 C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}{L_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+L_2\cancel{\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&\frac{j\omega L_2 C_3}{L_1+L_2}\\<br />Y_c&=&\frac{Z_1}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&\frac{j\omega L_1}{\left(1-{\omega}^2L_1 C_1\right)\left(-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}\right)}\\<br />&=&-\frac{j\omega L_1 C_3}{L_1\left({\omega}^2L_2 C_3-1\right)+L_2\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&-\frac{j\omega L_1 C_3}{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}<br />\end{eqnarray}$ 従って等価なπ形回路は $\begin{eqnarray}<br />Z_a&=&\frac{1}{Y_a}\\<br />&=&-\frac{1}{\frac{j}{\omega\left(L_1+L_2\right)}}\\<br />&=&j\omega\left(L_1+L_2\right)\\<br />&=&j\omega L_a\\<br />L_a&=&L_1+L_2\\<br />Z_b&=&\frac{1}{Y_b}\\<br />&=&\frac{1}{\frac{j\omega L_2 C_3}{L_1+L_2}}\\<br />&=&-\frac{j\left(L_1+L_2\right)}{\omega\left(L_2 C_3\right)}\\<br />&=&\frac{1}{j\omega\left(\frac{L_2 C_3}{L_1+L_2}\right)}\\<br />&=&\frac{1}{j\omega C_b}\\<br />C_b&=&\frac{L_2 C_3}{L_1+L_2}=\frac{C_3}{\frac{L_1}{L_2}+1}=\frac{C_3}{\frac{C_3}{C_1}+1}=\frac{C_1 C_3}{C_1+C_3}\\<br />Z_c&=&\frac{1}{Y_c}\\<br />&=&-\frac{1}{\frac{j\omega L_1 C_3}{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&-\frac{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}{j\omega L_1 C_3}\\<br />&=&\frac{L_1+L_2}{j\omega L_1 C_3}-\frac{\left(L_1+L_2\right){\omega}^2\cancel{L_1} C_1}{j\omega \cancel{L_1} C_3}\\<br />&=&\frac{1}{j\omega\left(\frac{L_1 C_3}{L_1+L_2}\right)}+j\omega\frac{\left(L_1+L_2\right)C_1}{C_3}\\<br />&=&\frac{1}{j\omega C_c}+j\omega L_c\\<br />C_c&=&\frac{L_1 C_3}{L_1+L_2}=\frac{C_3}{1+\frac{L_2}{L_1}}=\frac{C_3}{1+\frac{C_1}{C_3}}=\frac{{C_3}^2}{C_1+C_3}\\<br />L_c&=&\frac{\left(L_1+L_2\right)C_1}{C_3}=\frac{\left(L_1+L_2\right)L_2}{L_1}<br />\end{eqnarray}$ ということになる。今度は逆にπ形回路のインピーダンス行列をYa,Yb,Ycで表すと $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />Y_a+Y_b & -Y_b\\<br />-Y_b & Y_b+Y_c<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />\frac{Y_c+Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c} & \frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c} & \frac{Y_a+Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}<br />\end{array}\right]<br />\end{eqnarray}$ 従ってT形回路のインピーダンスZ1,Z2,Z3をπ形回路のYa,Yb,Ycで表すと $\begin{eqnarray}<br />Z_1&=&Z_{11}-Z_{12}\\<br />&=&\frac{Y_c}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />Z_2&=&Z_{12}\\<br />&=&\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />Z_3&=&Z_{22}-Z_{12}\\<br />&=&\frac{Y_a}{Y_a Y_b+Y_a Y_c+Y_b Y_c}<br />\end{eqnarray}$ 題意よりπ形回路のYa,Yb,Ycは $\begin{eqnarray}<br />Y_a&=&\frac{1}{j\omega L_1+\frac{1}{j\omega C_1}}\\<br />&=&\frac{j\omega C_1}{1-{\omega}^2L_1 C_1}\\<br />Y_b&=&\frac{1}{j\omega L_2}\\<br />&=&-\frac{j}{\omega L_2}\\<br />Y_c&=&j\omega C_3<br />\end{eqnarray}$ これを先のZ1,Z2,Z3の式に代入するとL1C1=L2C3が成り立つ場合 $\begin{eqnarray}<br />Z_1&=&\frac{Y_c}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&\frac{j\omega C_3}{\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}}}\\<br />&=&\frac{j\omega L_2 C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}{C_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&\frac{j\omega L_2 C_3}{C_1+C_3}\\<br />&=&j\omega L^{\'}_1\\<br />L^{\'}_1&=&\frac{L_2 C_3}{C_1+C_3}=\frac{L_2}{\frac{C_1}{C_3}+1}=\frac{L_2}{\frac{L_2}{L_1}+1}=\frac{L_1 L_2}{L_1+L_2}\\<br />Z_2&=&\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&-\frac{j}{\omega L_2\left(\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)}+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}\right)}\\<br />&=&-\frac{j\cancel{\left({\omega}^2L_1 C_1-1\right)}}{\omega\left(C_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}\right)}\\<br />&=&-\frac{j}{\omega\left(C_1+C_3\right)}\\<br />&=&\frac{1}{j\omega C^{\'}_2}\\<br />C^{\'}_2&=&C_1+C_3\\<br />Z_3&=&\frac{Y_a}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&\frac{j\omega C_1}{\left(1-{\omega}^2L_1 C_1\right)\left(\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)}+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}\right)}\\<br />&=&-\frac{j\omega L_2 C_1}{C_1\left({\omega}^2L_2 C_3-1\right)+C_3\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&-\frac{j\omega L_2 C_1}{\left(C_1+C_3\right)\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&\frac{1}{\left(C_1+C_3\right)\left(j\omega\frac{L_1}{L_2}+\frac{1}{j\omega L_2 C_1}\right)}\\<br />&=&\frac{1}{j\omega\frac{L_1\left(C_1+C_3\right)}{L_2}+\frac{C_1+C_3}{j\omega L_2 C_1}}\\<br />&=&\frac{1}{j\omega C^{\'}_3+\frac{1}{j\omega L^{\'}_3}}\\<br />C^{\'}_3&=&\frac{L_1\left(C_1+C_3\right)}{L_2}=\frac{C_3\left(C_1+C_3\right)}{C_1}\\<br />L^{\'}_3&=&\frac{L_2 C_1}{C_1+C_3}=\frac{L_2}{1+\frac{C_3}{C_1}}=\frac{L_2}{1+\frac{L_1}{L_2}}=\frac{{L_2}^2}{L_1+L_2}<br />\end{eqnarray}$ ということになる。ちなみにC'3の値が著者の解答とは違っているが、こちらが正しい。著者の解はL2/L1をL1/L2と転記ミスしている。それぞれ回路図に表すと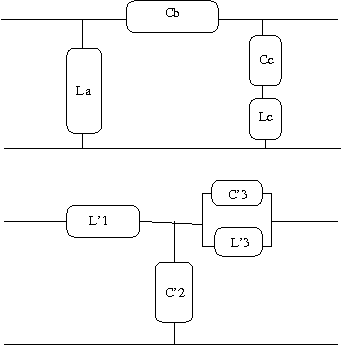と言う結果になる。 P.S. ふう、ほとんどが計算で大変だった。最初T形回路とπ形回路の素子定数の添字を一緒にして混乱したので、改めてπ形回路由来はa,b,cでT形回路由来は1,2,3とした。途中の式の操作はMaximaを使って確認するも、入力ミスがあったりして更に頭が混乱してしまった。最後に著者の解答に驚愕の誤記があるというどんでん返しで寝込むかと思った。結局CならCだけから、LならLだけから成るように式を整えるのは人間が意図的にやらないとどうしようもなかった。そういえばZobel変換というのは検索してもまったくひっかからない。おそらくΔ-Y等価変換と同じだと思われるが、Valkenburgによると1899年に既にA.E.KennelyがElectric World and Engineering誌の記事"The equivalence of triangles and three-point stars in conducting networks"で示しているのでZobel由来と言う人はほとんど居ないのだろう。Zobelが二端子対回路で同じことを示したのはそれからずっと後のことだし。

webadm	投稿日時: 2010-5-24 17:53
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	ハイブリッドパラメータ次ぎはハイブリッドパラメータ（Ｈ行列）に関する問題。いきなりエミッタ接地のトランジスタ等価回路ですよ。寝込みそう(;´Д`) 数式モデルというのは慣れてしまうまでが大変で、慣れてもしばらく遠ざかると違和感が復活するというやっかいない代物。よく数学が苦手とかいう人は、その人の中に既に数学があるからだというのは頷ける。その人が納得のいくやり方でやればいいわけで。そういう自由は本来数学にもあるはず。先人の見方や考え方にその人がシンクロできないだけで、時間はかかるけど自分でゼロから考え直してもいいはず。学校だと時間制限があるからそうはいかないけど、独学なら許される。そういう意味では既存のテキストで独学するには、どうしてもそれを書いた人や最初にそれを考えた人の思考回路のコピーを自分の頭の中に作り上げる必要があるわけで、これが苦痛なだけ。なんの話しだったっけ。ああ、トランジスタ等価回路ね。とりあえず問題の意味を自分なりにゼロから考え直してみよう。 1959年に出版されたドイツの理論電気学の教科書にも二端子対回路（Hパラメータ）でトランジスタの等価回路が既に説明されている。この当時既にPNPやNPNトランジスタ、ベース接地やエミッタ接地回路などが知られていた。それ以前には真空管があったわけだがトランジスタとは動作が異なるので別のモデルをこしらえる必要があったのは自明である。今時真空管から考える人は居ないので、歴史的な経緯をすっ飛ばしてトランジスタから入るわけである。バイポーラトランジスタの場合、図の様にエミッタ接地回路の場合はベース電流(Ib)に比例してコレクタ電流(Ic)が増大する電流増幅効果を発揮する。しかしながら能動素子と称しながらもトランジスタは電圧をかけないと何の機能もしない。従って回路上は入力及び出力端子対ともに電源が必要である。やっかいなことにバイポーラトランジスタは印可する電圧や流れる電流によって特性が変わる非線形素子である。従って予め与えられた動作点（電圧と電流）の近傍でのみ小信号を扱う限り線形素子と見なせる。そうした前提条件の上にトランジスタ等価回路を考えることになる。真空管もトランジスタも動作させるにはバイアス電圧を印可してある程度バイアス電流が流れている動作点でないと線形動作を得ることができない。それには以下の図にあるように出力を電圧として取り出すために負荷抵抗を電源と直列に接続して増幅された電流変化を電圧に変換する必要がある。これである程度解析に必要な数式モデルは立てられるが問題がある。実際に二端子対回路として縦続接続したり並列接続すると動作点（バイアス電圧やバイアス電流）が変化してしまう。この場合には二端子対回路の時に学んだ通りに、以下の通り理想変成器を端子対に挿入することでトランジスタの動作点を一定に保ったまま外部回路と自在に接続できる。ただしDC領域と周波数領域の振る舞いは対象外とする。入力と出力は供に動作範囲内の周波数スペクトルのみを持つ交流信号に限定される。理想変成器を挿入することで直流的にはアイソレートされているが交流的には直結と見なせる都合の良いモデルが得られる。これが題意の等価回路の意味するところであるが、T形回路になっている点とかの理由についてはここでは詳しく触れない。実際に自分の手でトランジスタの動作特性を実験で観測し電子回路や半導体素子理論を学ぶことをお勧めする。トランジスタそのものは当初理論的に意図して作られた素子ではなく、偶然他の目的の素子（三極ダイオード）を実験中に観測された現象である。現象を説明するためや意図した性能を備えた素子を作るために後追いで理論が構築された歴史的経緯がある。これはトランジスタに限らずよくあることなのだが。上記の等価回路では入力端子対の電流I1(ベース電流:Ib)に相互レジスタンス(rm)に比例した内部の等価電源の起電力が発生し出力端子対に電圧が発生する。出力端子対に外部回路を負荷として接続するとループを形成して出力端子対の電流I2(コレクタ電流:Ic)が決まることになる。そこでこの等価回路のハイブリッドパラメータを導いてみることにする。ハイブリッド行列で上記の二端子対回路を表すとすれば $\begin{eqnarray}<br />\left[\begin{array}<br />E_b\\<br />I_c<br />\end{array}\right]&=&\left[\begin{array}<br />h_{11} & h_{12}\\<br />h_{21} & h_{22}<br />\end{array}\right]\left[\begin{array}<br />I_b\\<br />E_c<br />\end{array}\right]<br />\end{eqnarray}$ EbとIb,Ecの関係は回路より重ね合わせの理で $\begin{eqnarray}<br />E_b&=&r_b I_b+r_e\left(I_b+I_c\right)\\<br />&=&r_b I_b+r_e I_b+r_e\left(\frac{r_m I_b}{r_e+r_c-r_m}-\frac{r_e I_b}{r_e+r_c-r_m}+\frac{E_c}{r_e+r_c-r_m}\right)\\<br />&=&\left(r_b+r_e+r_e\frac{r_m-r_e}{r_e+r_c-r_m}\right)I_b+\frac{r_e}{r_e+r_c-r_m}E_c\\<br />&=&\left(r_b+r_e\left(1+\frac{r_m-r_e}{r_e+r_c-r_m}\right)\right)I_b+\frac{r_e}{r_e+r_c-r_m}E_c\\<br />&=&\left(r_b+r_e\left(\frac{\cancel{r_e}+r_c-\cancel{r_m}+\cancel{r_m}-\cancel{r_e}}{r_e+r_c-r_m}\right)\right)I_b+\frac{r_e}{r_e+r_c-r_m}E_c\\<br />&=&\left(r_b+\frac{r_e r_c}{r_e+r_c-r_m}\right)I_b+\frac{r_e}{r_e+r_c-r_m}E_c\\<br />&=&h_{11}I_b+h_{12}E_c\\<br />h_{11}&=&r_b+\frac{r_e r_c}{r_e+r_c-r_m}\\<br />h_{12}&=&\frac{r_e}{r_e+r_c-r_m}<br />\end{eqnarray}$ 同様にIcとIb,Ecの関係も重ね合わせの理で $\begin{eqnarray}<br />I_c&=&\frac{r_m I_b}{r_e+r_c-r_m}-\frac{r_e I_b}{r_e+r_c-r_m}+\frac{E_c}{r_e+r_c-r_m}\\<br />&=&\frac{r_m-r_e}{r_e+r_c-r_m}I_b+\frac{1}{r_e+r_c-r_m}E_c\\<br />&=&h_{21}I_b+h_{22}E_c\\<br />h_{21}&=&\frac{r_m-r_e}{r_e+r_c-r_m}\\<br />h_{22}&=&\frac{1}{r_e+r_c-r_m}<br />\end{eqnarray}$ 従ってハイブリッド行列表記では $\begin{eqnarray}<br />\left[\begin{array}<br />h_{11} & h_{12}\\<br />h_{21} & h_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />r_b+\frac{r_e r_c}{r_e+r_c-r_m} & \frac{r_e}{r_e+r_c-r_m}\\<br />\frac{r_m-r_e}{r_e+r_c-r_m} &\frac{1}{r_e+r_c-r_m}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。有効性うんぬんについては先に触れた通りに・理想変圧器を必要とするので現実の回路の設計には使えない・直流増幅器やレベルシフト回路には使えないという具合に悪口ばっかり目立ってしまう。それでも有効性としてあげれば・動作点やバイアスは内部で閉じているので外部では配慮する必要がない・トランジスタを使用する上での動作点やバイアスに関する回路内部の設計と外部インタフェース仕様を分離して考えることができるなどがあげられる。先の欠点は、理想変圧器の代わりに直流をブロックし交流信号だけ通過させるカップリングコンデンサを端子対に挿入する方法で緩和することが古くから行われている。よくトランジスタの初歩の回路に登場するやつである。実際オーディオ帯域の交流信号ではうまくゆく。回路の意味については一般のトランジスタ回路の参考書に譲る。しかし理想変圧器と違ってキャパシタンスを用いる関係上、周波数が低くなるとインピーダンスが高くなり交流信号が流れにくくなる。低域で利得を落とさないためにはできるだけ容量の大きなコンデンサを使う必要があるが、これがオーディオアンプでは災いの元である。安易に非線形特性（電圧係数や誘電体吸収）が大きいコンデンサをカップリング用に使用すると、信号が歪んでしまうことになる。所謂忠実度が低下するというやつである。それと定常状態では理論上はうまくいっても電源投入直後は充電電流が流れ込むためにトランジスタが一辺にオンして、オーディオパワーアンプでは異常な出力が出てスピーカーが破れてしまうことになりかねない。この過渡現象の問題は定常状態だけ考えていてもどうにもならないので、高級なオーディオアンプは電源投入直後は出力をミュートするなどなんらかの回避策が施されている。それと依然として直流増幅はできない。例えば微少な直流電圧を測定するような電圧計を作ろうとした場合、直流をブロックしてしまってはなんにもならない。これにはやはり別途DC領域まで対応した回路を考える必要がある。またトランジスタが登場した直後から既に集積回路への応用もはじまっていた。しかしながら、オーディオアンプを集積回路化しようとした場合、カップリングコンデンサを含んだ個別部品で組んでいた増幅回路をそのままシリコンダイ上に載せることは不可能である。なぜなら集積回路上には大容量のコンデンサを実装することができないからである。集積回路では個別部品による増幅回路の設計がまったく通用しない。これも直流的に結合した回路を考えないといけなくなる。ということで、基礎的な理論を理解をする上ではシンプルで扱い易く都合が良いものの、実務ではhパラメータはほとんど使う機会は無いということになる。まあそういうことが解っただけでももうけものである。

(1) 2 3 4 ... 7 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を