| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-8-26 4:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3084 |
【30】波形の同形性 次の問題はある意味奥が深い問題である。
以下のFourier級数展開で与えられた電圧と電流の波形が同形であるか確かめひずみ率を求めよというもの。 e=120*sin(ωt-60°)+60*cos(3ωt-180°)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) なんとなく題意の意味はわかるが、厳密に同形であることを調べるにはどうすればいいのかというのが難問である。 eとiの波形が同形であることを確認するには、eとiの波形の間に1対1の変換が存在することを証明する必要がある。 どうすんだこれ。 実は同形性の問題は奥が深く、信号処理で必ず習うナイキスト・シャノンの標本化定理はナイキストによって予測されていた連続時間系システムと離散時間系システムの同形性を数学的に証明したことに普遍的な意義がある。 デジタルコンピューターの登場と性能向上によって微分方程式の数値解法が開実用的になり、さまざまな物理演算やシミュレーションが連続時間系ではなく離散時間系の差分方程式の計算で行えるようになってきたが、反面現実の連続時間系システムとの同形性を確認しないまま数値だけを鵜呑みにしてしまう傾向が強くなっている。 離散時間系での差分方程式はさまざまな数学的な直交座標系では連続時間系の微分方程式と同形であることが知られているが、現実の世界の空間はさまざまな例外があって数学な空間とは異なることが多い。電磁界シミュレーターとかでは周囲を自由空間で囲まれていることを前提としているが、実際の機器はさまざまな導体や絶縁体で囲まれていたりする。ボールを投げるとボールが進む空間ではさまざまな方向の風にさらされる。恒星から発せられる光は太陽のそばでは巨大な重力によって歪んだ空間を直進し続けるが結果的に外から見ると曲がって進んでいるように見える。一見して予想と違ってみえる現実と理想との間にある未知の変換を施せば、互いの点と点は一対一の対応になるはずである。 信号処理ではこうした変換(標本化関数)がまだ数えるほどしか発見または考案されておらず、2次元や三次元などではほとんど未開拓であるだけに将来的に面白い分野である。 いずれ遠い将来に人間の知覚や認識、思考が連続時間系システムでどのように行われているか明らかになれば、それらはすぐに離散時間系システムで同形のことが可能なはずである。つまり人間の人格そのものをコンピューター内に移すこともいずれ可能になるだろう。 でなんの話だっけ? ああ、波形の同形性ね。 ちょっと熱が出てきたので休んでまた続きを。 前置きが長かったので式を再掲し整理してみると e=120*sin(ωt-60°)+60*cos(3ωt-180°)-30*sin(5ωt-140°) =120*sin(ωt-60°)-60*cos(3ωt)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) 2つの式を見比べると係数が6:1で位相が90°違っていることが定性的にわかる。 これをなんとか形式的に表すことができないだろうか、例えば変換マトリックスと逆変換マトリックスで。 例えばeとiを正方マトリックスで表すと e=([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) i=([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) ここでeからiへの変換マトリックスTが存在すると仮定すると T=([t11,t12,t13],[t21,t22,t23],[t31,t32,t33]) i=T.e Tに逆行列が存在するとすれば e=T^-1.i が成り立つようなTを見つければeとiは同形であると言える。 従って T=e^-1.i で表すことができる。 ここでeの逆行列は e^-1=([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)])^-1 =([1/(120*sin(ωt-60°)),0,0],[0,-1/(60*cos(3ωt)),0],[0,0,-1/(30*sin(5ωt-140°))]) これをiに乗じれば T=e^-1.i =([1/(120*sin(ωt-60°)),0,0],[0,-1/(60*cos(3ωt)),0],[0,0,-1/(30*sin(5ωt-140°))]).([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =([sin(ω+30°)/(6*sin(ωt-60°)),0,0],[0,sin(3ωt)/(6*cos(3ωt)),0],[0,0,sin(5ωt-50°)/(6*sin(5ωt-140°))]) ということになる。これには逆行列も存在し T^-1=([(6*sin(ω-60°))/sin(ωt+30°),0,0],[0,(6*cos(3ωt))/sin(3ωt),0],[0,0,(6*sin(5ωt-140°))/sin(5ωt-50°)]) ということになる。実際に検算してみると T.e=([sin(ω+30°)/(6*sin(ωt-60°)),0,0],[0,sin(3ωt)/(6*cos(3ωt)),0],[0,0,sin(5ωt-50°)/(6*sin(5ωt-140°))]).([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) =([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =i T^-1.i=([(6*sin(ω-60°))/sin(ωt+30°),0,0],[0,(6*cos(3ωt))/sin(3ωt),0],[0,0,(6*sin(5ωt-140°))/sin(5ωt-50°)]).([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) =e 当たり前だがそういうことになる。 従ってeとiは同型であると言える。 ひずみ率は基本波の実効値と高調波の実効値の比なので ひずみ率=sqrt(|E3|^2+|E5|^2)/|E1| =sqrt((60/√2)^2+(30/√2)^2)/(120/√2) =sqrt(60^2+30^2)/120 =sqrt(3600+900)/120 =sqrt(4500)/120 =10*3*sqrt(5)/120 =sqrt(5)/4 =0.56 同様に電流から求めると ひずみ率=sqrt(|I3|^2+|I5|^2)/|I1| =sqrt((10/√2)^2+(5/√2)^2)/(20/√2) =sqrt(10^2+5^2)/20 =sqrt(100+25)/20 =sqrt(125)/20 =5*sqrt(5)/20 =sqrt(5)/4 =0.56 ということになる。 P.S 同形と同型は異なる。 電圧の式を一部変えて e=100*sin(ωt-60°)-60*cos(3ωt)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) とした場合、eとiは依然として同型であるが、ひずみ率を計算するとそれぞれ異なるので同形ではなくなる。 元の電圧の波形と一部Fourier係数を変えた電圧の波形をプロットしてみるほとんど見かけ上変わらない、同型であるゆえんである。 wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),-30*sin(5*x-(7*%pi)/9) +100*sin(x-%pi/3)-60*cos(3*x)], [x,-5,5])$ 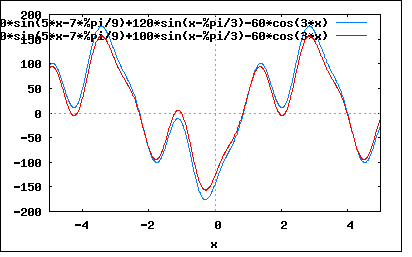 もともとの電圧と電流の波形をプロットして見比べてみると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),20*sin(x+2*%pi*30/360) -10*sin(3*x)-5*sin(5*x-2*%pi*50/360)], [x,-5,5])$ 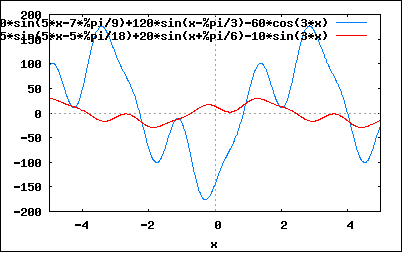 一見するとまるで似ても似つかない。 縦軸を対数表示にすると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),20*sin(x+2*%pi*30/360) -10*sin(3*x)-5*sin(5*x-2*%pi*50/360)], [x,-5,5], [gnuplot_preamble, "set logscale y; set grid;"])$ 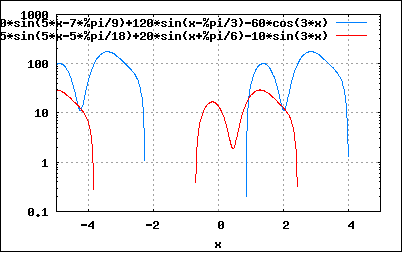 波形のレンジと位相が異なるものの同形の波形に見える。 一方同型だが同形ではない2つの電圧の波形を同様に対数圧縮してプロットすると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),-30*sin(5*x-(7*%pi)/9) +100*sin(x-%pi/3)-60*cos(3*x)], [x,-5,5],[gnuplot_preamble, "set logscale y; set grid;"])$ 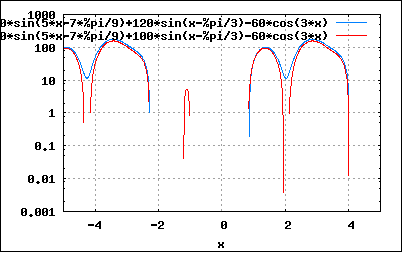 明らかに同じ波形ではないことが見てとれる。 人間の聴力とかは対数圧縮的な機能もっているので小さな音でも大きな音でも微妙にスペクトルが異なる音を聞き分けることができるのかもしれない。 音楽とか書物とかがソフトウェアなどですでにあるものの盗作であるかどうかを問題にするときにも同形性や同型性が問題になってくる。奥が深い問題である。 P.S この問題に真剣に組するとガロア理論に端を発する形式群論とか抽象数学の世界をマスターしないとどっかで行き倒れになりそうである。実際2次元以上の複素数やもっと高次元の同型性判定問題を扱うとなるとほとんど現代でも未踏の領域である。リーマンの生きた19世紀からほとんど進歩していないのだ。というのも難問すぎてみんなさじを投げてしまっているからだろう。グラフ理論なども一時期は盛り上がったが同形性問題に深い深い底なし沼があることがわかってから誰も寄り付かなくなった。恐ろしい世界である。 信号処理も最先端になると群論はむろんリーマン面とか先端数学を知らないとお友達になれない世界。 こんど群論に関しても古本を入手して学んでおくことにしよう。 P.S 2 よく考えれば、スペクトルが相似であれば波形は同形であると言えるのではないか。|I1'|,|I3'|,|I4'|が|I1|,|I3|,|I5|と以下の関係があるとすれば |I1'|=a|I1| |I3'|=a|I3| |I5'|=a|I5| とするとひずみ率は ひずみ率=sqrt(|I3'|^2+|I5'|^2)/|I1'| =sqrt((a|I3|)^2+(a|I5|)^2)/(a|I1|) =sqrt(|I3|^2+|I5|^2)/|I1| 従ってスペクトルが相似な元の波形と相似な波形ではひずみ率は同じになるということになり、すなわち同形であると言える。 一方上記の様にスペクトルが相似でない場合にはひずみ率は異なってしまうので同じ波形ではないということになる。 おそらく音声帯域であればスピーカーでならして耳で聞いてみればスペクトルが相似な同形の波形は同じ音色に聞こえ、そうでないものは異なる音色に聞こえることだろう。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

