| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-13 5:32 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
【56】対称三相交流ひずみ波(その7) 次ぎの問題は前問のようなY形三相発電機の線間電圧の波形率および波高率を求めよというもの。
前問の続きのような問題なので、まず線間電圧は前問の解から e12=e1-e2=√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6)) e23=e2-e3=√6*(|E1|*sin(ωt-π/2)+|E5|*sin(5ωt+π/2)) e31=e3-e1=√6*(|E1|*sin(ωt+5π/6)+|E5|*sin(5ωt-5π/6)) 波形率の定義を思い出すと 波形率=実効値/平均値 であるので、e12の実効値と平均値をそれぞれ求めると |e12|=sqrt((√6|E1|)^2+(√6|E5|)^2) =√6*sqrt(|E1|^2+|E5|^2) 平均値は対称波なので半周期分を積分 e12ave=(2/T)∫e12dt (t=0,T/2) =(2/T)∫√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6))dt =(2√6/T)*(|E1|∫sin(ωt+π/6)dt+|E5|∫sin(5ωt-π/6)dt) =(2√6/T)*(|E1|√3T/2π+|E5|√3T/10π) =2√6*(|E1|√3/2π+|E5|√3/10π) =(√2√6/π)*(|E1|+|E5|/5) =(2√3/π)*(|E1|+|E5|/5) ということになる。 従って波形率は 波形率=√6*sqrt(|E1|^2+|E5|^2)/(2√3/π)*(|E1|+|E5|/5) ということになる。 一方波高率の定義は 波高率=最大値/実効値 なので最初に線間電圧の最大値を知る必要がある。 e12をtで微分すると d(e12)/dt=d(√6*(E1*sin(ωt+π/6)+E5*sin(5ωt-π/6))/dt =√6*(ω*E1*cos(ωt+π/6)+5ω*E5*cos(5ωt-π/6)) =√6ω*(E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)) 従って極大極小値をとるのは E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)=0 を満たすtである。 これどうやって解くんだ? この主の三角関数が式に出てくる方程式は三角方程式と呼ぶらしく、高校の数学で習うらしい。憶えてないぞ。 y=E1*cos(ωt+π/6) y=-5*E5*cos(5ωt-π/6) を同時に満たすtとyを求めるというふうに考えることもできる。その解にはy=0となるtもあり得る。それ以外のy≠0なtもあるだろう。 著者の解と違ったアプローチをしようと悩みまくっている。 思いついたのは 上の関数は元々は平面座標上の一次関数を三次元円筒曲面上に写像した3次元螺旋曲線をそれと並行な2次元平面に投影したものと考えることができる。なので元の一次関数に変換して考えれば二元連立方程式を解くだけで済むのではないか? という点である。恐ろしくやっかいなので現在考え中。 小休止して、基本波と5次高調波からなるひずみ波がどんな波形かプロットしてみると wxplot2d([sin(5*x-%pi/6)+sin(x+%pi/6)], [x,-5,5])$ 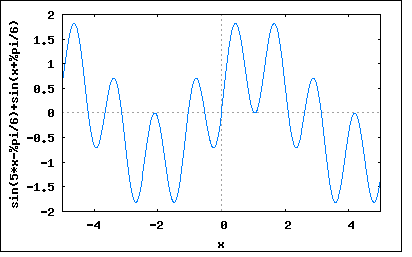 基本波の上に高調波が乗って波打っている、俗に言う「うなり」を生じている。基本波と高調波に微妙な位相のずれがあるので、最大値と最小値は基本波と高調波の最大振れの合計以内に収まる。 複雑な波形だが元は2つの正弦波からの合成である。半径の異なる2つの同心円筒曲面上に描かれた螺旋を極座標面で合成して得られる三次元曲線を平面に投影するとこうなる。2つの異なる周期を持つその三次元曲線を容易に想像することは難しい。ちょうど18世紀以前の天文学者達が天空球平面上で映し出される惑星の奇妙な軌跡から惑星の軌道を思い描くのに多大な年月を要したのと同じである。 さて少しこの問題を探ってみると、驚愕の事実が発覚。たまたまトイレでトイレットペーパーを交換しようとしたときにトイレットペーパーの芯に目をやったら、ちょうど良い具合に芯を構成する紙をつなぎ合わ境界線が二重螺旋を描いている。しかもひとつの螺旋はちょうど芯の両端で一周期になっている。芯の内側を見ると二重螺旋が現れるのは細長い同じ幅の紙のリボンを二重螺旋状にして接合しているためだとわかる。メーカーのロゴが印刷された独立した2つの同一幅の紙のリボンの螺旋がつなぎあわさって円筒が面が構成されている。これを設計したひとは数学が出来る人にちがいない。 更にトイレットペーパーの芯を眺めながら今回の三角方程式の解法を検討すると、それまで予想もしていなかった問題点を発見。螺旋状に巻かれた線を平面に展開すれば直線になるが、それだと二本の異なる螺旋をそれぞれ平面に展開した際の交点(連立方程式の根)はひとつしかない(根がひとつしかない)という疑問があった。しかしよく考えれば、円筒状の同一の螺旋へと写像される平面状の直線は無数にあるということに気づくべきだった。トイレットペーパーの芯を見てすぐにそれを直感した。ひとつの一次直線をある一定の等間隔(円筒の直径に相当する距離)で並行に無数に並べたものを円筒面に写像すると螺旋はたった一本しか現れない。ということは螺旋から平面への逆写像は多価性をもっているということのあらわれである。 そうすると二本のまったく異なる周期を持つ螺旋をそれぞれ平面に逆写像すると二種類の無数に並行する一次曲線の格子になる。従ってその交点は無数にある...orz ということで最初に考えたこのアプローチは従来的な三角方程式の解法と同じ結果を得るだろうと予測される。 一瞬超越関数である余弦関数を線形一次の代数方程式に逆変換できるとおもったのだが甘かった。しかしこれはなんとなく奥深い予感がするので、あせらずに時間をかけて研究したいテーマではある。 今しばらくはこの演習問題を解くのに専念しよう。 話を三角方程式にもどそう。 三角方程式というのは数学用語ではなくて日本独自の受験用語らしい。それも今日のように小子化時代では受験生から嫌われる数学は入学試験科目から外される傾向があるなか死語になりつつあるらしい。 三角方程式を解くにはベクトル図を描くとよいらしい。 E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)=0 これを以下の様に書き換えると E1*cos(ωt+π/6)=-5*E5*cos(5ωt-π/6) この条件をベクトル図に描くと 図から 5*E5*cos(5ωt-π/6+π)=5*E5*cos(5ωt+5π/6) =-5*E5*cos(5ωt-π/6) ということがわかる。そこで θ=ωt+π/6 と置くと 5θ=5(ωt+π/6)=5ωt+5π/6 従って E1*cos(θ)-5*E5*cos(5θ)=0 ということになる。 どうすんだこれ。 とりあえずcos(5θ)を展開すると E1*cos(θ)-5*E5*cos(5θ) =E1*cos(θ)-5*E5*cos(2θ+3θ) =E1*cos(θ)-5*E5*(cos(2θ)*cos(3θ)-sin(2θ)*sin(3θ)) =E1*cos(θ)-5*E5*((2*cos(θ)^2-1)*(4*cos(θ)^3-3*cos(θ))-2*sin(θ)*cos(θ)*(-4*sin(θ)^3+3*sin(θ))) =E1*cos(θ)-5*E5*(8*cos(θ)^5-6*cos(θ)^3-4*cos(θ)^3+3*cos(θ)+8*sin(θ)^4*cos(θ)-6*sin(θ)^2*cos(θ)) =E1*cos(θ)-5*E5*(8*cos(θ)^5-10*cos(θ)^3+3*cos(θ)+8*cos(θ)^4*cos(θ)-6*sin(θ)^2*cos(θ)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*sin(θ)^4-6*sin(θ)^2+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*(1-cos(θ)^2)^2-6*(1-cos(θ)^2)+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*(1-2*cos(θ)^2+cos(θ)^4)-6+6*cos(θ)^2+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8-16*cos(θ)^2+8*cos(θ)^4-6+6*cos(θ)^2+3)) =cos(θ)*(E1-5*E5*(16*cos(θ)^4-20*cos(θ)^2+5)) =cos(θ)*(E1-80*E5*cos(θ)^4+100*E5*cos(θ)^2-25*E5)) =0 従ってこれをcos(θ)について解くと cos(θ)=0 cos(θ)^2=-100*E5/2*(-80*E5)±sqrt((100*E5/2*(-80*E5))^2-(E1-25*E5)/(-80*E5)) =5/8±sqrt((5/8)^2+(E1/E5-25)/80) =5/8±sqrt(25/64+(E1/E5-25)/80) =5/8±(1/4)*sqrt(25/4+(E1/E5-25)/5) =5/8±(1/4)*sqrt((25+4*E1/E5)/20) =5/8±(1/8)*sqrt((25+4*E1/E5)/5) =5/8±(1/8)*sqrt(5+4*E1/5*E5) =(5±sqrt(5+4*E1/5*E5))/8 従って cos(θ)=sqrt(5±sqrt(5+4*E1/5*E5))/2√2 ということになる。 すなわち線間電圧e12が極大極小値をとるのは θ=±π/2 θ=±acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) ということになる(主値)。 線間電圧e12の二次導関数を求めると =d^2(e12)/dt^2 =d^2(√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6)))/dt^2 =-√6*ω^2*(|E1|*sin(ωt+π/6)+25*|E5|*sin(5ωt-π/6)) θ=ωt+π/6 と置くと d^2(e12)/dt^2 =-√6*ω^2*(|E1|*sin(θ)+25*|E5|*sin(5θ-π)) =-√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) ということになる。 θ=π/2を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(π/2)-25*|E5|*sin(5*π/2)) =-√6*ω^2*(|E1|-25*|E5|) θ=-π/2を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(-π/2)-25*|E5|*sin(-5*π/2)) =√6*ω^2*(|E1|-25*|E5|) 従って |E1|-25*|E5| > 0 の場合 すなわち |E1| > 25*|E5| の場合 θ=π/2で極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) =√6*(|E1|-|E5|) をとる。 逆に |E1|-25*|E5| < 0 の場合 すなわち |E1| < 25*|E5| の場合 θ=-π/2で極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) =√6*(|E5|-|E1|) ということになる。 同様に θ=±acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) の場合も θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) θ=-acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) を代入すると d^2(e12)/dt^2=√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) 従って |E1|*sin(θ)-25*|E5|*sin(5θ) > 0の場合 すなわち |E1|*sin(θ) > 25*|E5|*sin(5θ)の場合 θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)が極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) をとる。 |E1|*sin(θ)-25*|E5|*sin(5θ) < 0の場合 すなわち |E1|*sin(θ) < 25*|E5|*sin(5θ)の場合 θ=-acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)が極大値 e12p=√6*(|E5|*sin(5θ)-|E1|*sin(θ)) をとる。 ということになる。 またsin(θ),sin(5θ)ともにπ/2の場合に最大値1を取るため |E1| > 25*|E5| の場合 θ=π/2の極大値 e12p=√6*(|E1|-|E5|) が最大値となる。 他方sin(θ),sin(5θ)ともに-π/2の場合に最小値-1をとるため |E1| < 25*|E5| の場合 θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)の極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) が最大値となる。 従って波高率は上記の2つのケースについてそれぞれ |E1| > 25*|E5| の場合 波高率=最大値/実効値=e12p/|e12| =√6*(|E1|-|E5|)/√6*sqrt(|E1|^2+|E5|^2) =(|E1|-|E5|)/sqrt(|E1|^2+|E5|^2) |E1| < 25*|E5| の場合 波高率=最大値/実効値=e12p/|e12| =√6*(|E1|sin(θ)-|E5|*sin(5θ))/√6*sqrt(|E1|^2+|E5|^2) =(|E1|*sin(θ)-|E5|*sin(5θ))/sqrt(|E1|^2+|E5|^2) ということになる。 著者の解法によるθの式が異なるが、倍角の三角関数の公式より cos(θ)^2=(cos(2θ)+1)/2 ∴cos(θ)=sqrt((cos(2θ)+1)/2) 従って θ=acos(θ)=acos(sqrt((cos(2θ)+1)/2) これに著者のθの解を代入すると acos(θ)=acos(sqrt((cos(acos((1±sqrt(5+4E1/5E5))/4))+1)/2)) =acos(sqrt(((1±sqrt(5+4E1/5E5))/4)+1)/2)) =acos(sqrt((1/4±sqrt(5+4E1/5E5)/4)+1)/2)) =acos(sqrt((5/4±sqrt(5+4E1/5E5)/4)/2)) =acos(sqrt(5/8±sqrt(5+4E1/5E5)/8)) =acos(sqrt(5±sqrt(5+4E1/5E5))/2√2) 従って θ=±acos(sqrt(5±sqrt(5+4E1/5E5))/2√2) とこちらで求めたものと同一であることが確かめられる。 最初違う式が導かれたのでどっか間違っていないかくまなく調べたがこの検証で一安心した。 極大極小値と最大値最小値は意味が異なるので要注意だ。極大極小値は山と谷だがピークやボトムではない点に注意。 ふう、だいぶ長くかかったがこれで対称三相交流ひずみ波の問題は終了。あとはFourier変換に関する問題を残すのみ。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

