Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 一端子対回路：演習問題

投稿者	スレッド
webadm	投稿日時: 2010-3-30 9:20
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	【７】正実関数前の問題で２ヶ月もかかったしまったが続きをやろう。アルバイトに精を出していたというのもあるけど、最後の設問に見事に嵌ってしまった。それでも誰からも忘れ去られていた問題があるのを見つけた気がする。次ぎの問題も正実関数に関するもの。以下の３つの有理関数が正実関数である条件を求めよというもの。 $\text{(1)}\,\,\frac{\left(s+2\right)^2}{s+x}$ s=-2に零点（重根）、s=-xに極を持つ有理関数。正実関数の性質として複素平面の右半面に特異点を持たないということから、 $x\ge0$ でなければならないことは自明である。ただしこれは必要条件であって十分条件ではない。正実関数とはとどのつまり受動素子(R/C/L)だけで回路が合成できるということなので、部分分数に展開(Foster展開）してみればわかるはず。 $\begin{eqnarray}\frac{\left(s+2\right)^2}{s+x}&=&\frac{s^2+4s+4}{s+x}\\&=&s+\frac{\left(4-x\right)s+4}{s+x}\\&=&s+\left(4-x\right)+\frac{4-\left(4-x\right)x}{s+x}\\&=&s+\left(4-x\right)+\frac{4-4x+x^2}{s+x}\\&=&s+\left(4-x\right)+\frac{\left(x-2\right)^2}{s+x}\end{eqnarray}$ 従って係数が正の実数であるためには $\begin{eqnarray}\left(4-x\right)&\ge&0\end{eqnarray}$ を満たせば十分である、先の必要条件と併せて $0\le{x}\le{4}$ ということになる。実はこれでは十分ではない。上記の実数部に関して確かめられていないからである。 s=jωを代入して実数部だけを得ると $\begin{eqnarray}Re\left(j\omega+\left(4-x\right)+\frac{\left(x-2\right)^2}{j\omega+x}\right)&=&\left(4-x\right)+\frac{x\left(x-2\right)^2}{\omega^2+x^2}\,\ge\,0\end{eqnarray}$ ということになる。従って問題の関数が正実関数であるためのxの必要十分条件は分母を取り払って整理すると $\begin{eqnarray}\left(\omega^2+x^2\right)\left(\left(4-x\right)+\frac{x\left(x-2\right)^2}{\omega^2+x^2}\right)&=&4\omega^2-x\omega^2+\cancel{4x^2}-\cancel{x^3}+\cancel{x^3}-\cancel{4x^2}+4x\\&=&\left(4-x\right)\omega^2+4x\\&=&\left(4-x\right)\left(\omega^2+\frac{4x}{4-x}\right)\\&=&\left(4-x\right)\left(\omega+j\sqrt{\frac{4x}{4-x}}\right)\left(\omega-j\sqrt{\frac{4x}{4-x}}\right)\,\ge\,0\end{eqnarray}$ と書き換えることができ、上記を満たすには $\begin{eqnarray}\left(4-x\right)\ge0\\\frac{4x}{4-x}\ge0\end{eqnarray}$ でなければならない。従って $0\le{x}\le{4}$ ということになる。 $\text{(2)}\,\,\left(\frac{s+2}{s+x}\right)^2$ 前の設問は零点のみが重根を有していたが、今度は極も重根を持つ。Foster展開すると $\begin{eqnarray}\left(\frac{s+2}{s+x}\right)^2&=&\frac{\left(s+2\right)^2}{\left(s+x\right)^2}\\&=&\frac{s^2+4s+4}{s^2+2xs+x^2}\\&=&1+\frac{\left(4-2x\right)s+4-x^2}{s^2+2xs+x^2}\\&=&1+\frac{\left(4-2x\right)}{s+x}+\frac{x^2-4x+4}{\left(s+x\right)^2}\\&=&1+\frac{2\left(2-x\right)}{s+x}+\frac{\left(x-2\right)^2}{\left(s+x\right)^2}\end{eqnarray}$ 従って正実関数であるためには $\begin{eqnarray}x&\ge&0\\\left(2-x\right)&\ge&0\\\end{eqnarray}$ 従って $0\le{x}\le{2}$ ということになる。これは著者の解とはだいぶ異なっているなるほど(1)と違って、第一項と第三項の実数バイアスがあるので第二項の実数部が負になっても有る程度までなら正実関数の条件を満たすので上の条件は十分条件ではないことは明らかである。ではいくつまでなら許されるか。以前にインピーダンスのベクトル軌跡を描いた要領でs=jωとしてωを0から∞に変化させた場合の軌跡を描いてみれば軌跡が左半面にはみ出さないxの範囲が見極められそうではある。第一項は実定数なので自明。第二項は直線を描くx+jωの逆数なので円を描くことがわかる。第三項は円に良く似た心臓形を描く。第三項の単体ベクトル軌跡をx=4で描くと 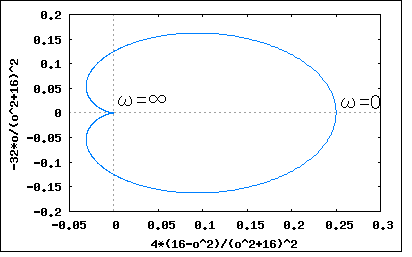ωが無限遠点に近づくと左半面回りで原点に収束するのがわかる。一方関数全体をx=4としてベクトル軌跡をプロットしてみると第三項の影響で少し歪んだ円となる。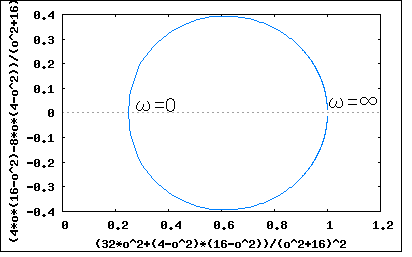もう少し左に寄って大丈夫(円の直径を大きくできる）なのがわかる。一方x=1とするとベクトル軌跡は実軸の1に垂直な線を境に鏡で映したように正反対側に円を描く。 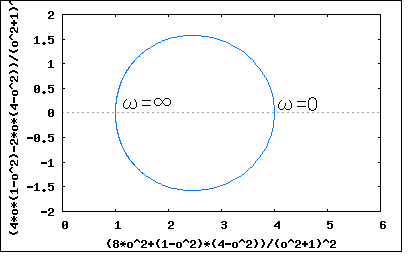xが2より小さい場合実軸の1より右側に円を描き2に近づくにつれ円がしぼみやがて定抵抗(Z=1)となる。xが2を超えると実軸の1より左側に円を描くようになる。これらの観点からs=jωとして展開してみると $\begin{eqnarray}Re\left(Z(j\omega)\right)&=&Re\left(1+\frac{2\left(2-x\right)}{j\omega+x}+\frac{\left(x-2\right)^2}{\left(j\omega+x\right)^2}\right)\\&=&1+\frac{2(2-x)x}{x^2+\omega^2}+\frac{(x-2)^2 (x^2-\omega^2)}{(x^2+\omega^2)^2}\\&=&1+\frac{(2-x)(3x-2)}{x^2+\omega^2}+\frac{2(x-2)^2 x^2}{(x^2+\omega^2)^2}\,\ge\,0\,,\,\forall\omega\end{eqnarray}$ (2010/4/5 展開の誤りを訂正）が成り立つxを求める不等式の解を求める問題に帰着する。∀ωは「すべてのωに対して」を論理学的に表したものである。数学的に解くとまず上記を満たすxが存在するかどうか判定証明しないといけないが、存在するのは上記検討結果から自明なので、後は解かどのような集合からなるか調べるだけとなる。こうして考えると前の設問(1)も簡単なケースの同種問題である。著者の解はどうにも見通しが悪くて未だにどうやって導きだしたのか理解できない式が使われているので納得いかない。もはや我流で納得の行く方法で解くしない。上の条件式を見るとx=0は条件を満たさないことが判明する。視覚的に関数を3Dグラフでプロットしてみると (x,ω)=(0,0)は極になるのでその領域を避けて、その近傍の関数平面をプロットしてみたものである。黒い領域が負の値を取り正実関数とならない領域である。上記の式のxに関する積分関数を考え、すべてのωに関して単調増加関数となるxの範囲を求めることと言い換えても良い。益々判らなくなってきた。とりあえず高次不等式の解法の基本に立ち戻って考えてみよう。先の条件式に分母の最小公倍数を乗じて分母を取り払うと $\begin{eqnarray}\left(x^2+\omega^2\right)^2\left(1+\frac{(2-x)(3x-2)}{x^2+\omega^2}+\frac{2(x-2)^2 x^2}{(x^2+\omega^2)^2}\right)&=&\left(x^2+\omega^2\right)+\left(x^2+\omega^2\right)\left(2-x\right)\left(3x-2\right)+2\left(x-2\right)^2 x^2\\&=&x^4+2x^2\omega^2+\omega^4+\left(x^2+\omega^2\right)\left(8x-4-3x^2\right)+2\left(x^2-4x+4\right)x^2\\&=&\cancel{x^4}+2x^2\omega^2+\omega^4+\cancel{8x^3}-4x^2\cancel{-3x^4}+8x\omega^2-4\omega^2-3x^2\omega^2+\cancel{2x^4}\cancel{-8x^3}+8x^2\\&=&\omega^4+8x\omega^2-4\omega^2-x^2\omega^2+4x^2\\&=&\omega^4+\omega^2\left(8x-4-x^2\right)+4x^2\\&=&\left(\omega^2+\left(x-2\right)\omega+2x\right)\left(\omega^2-\left(x-2\right)\omega+2x\right)\,\ge\,0\,,\,\forall\omega\end{eqnarray}$ と書き換えることができる。すなわち、 $\begin{eqnarray}\omega^2\pm\left(x-2\right)\omega+2x\,\ge\,0\,\,\forall\omega\\\omega^2\pm\left(x-2\right)\omega+2x\,\le\,0\,\,\forall\omega\end{eqnarray}$ という２つのケースに分かれるということが判明する。それぞれの条件式がωとxの関数である点が問題をややこしくしている。更に条件式を操作すると $\begin{eqnarray}\left(\omega\pm\frac{x-2}{2}\right)^2+2x-\frac{\left(x-2\right)^2}{4}\,\ge\,0\,\,\forall\omega\\\left(\omega\pm\frac{x-2}{2}\right)^2+2x-\frac{\left(x-2\right)^2}{4}\,\le\,0\,\,\forall\omega\end{eqnarray}$ 更に整理すると $\begin{eqnarray}\left(\omega\pm\frac{x-2}{2}\right)^2-\frac{x^2-12x+4}{4}\,\ge\,0\,\,\forall\omega\\\left(\omega\pm\frac{x-2}{2}\right)^2-\frac{x^2-12x+4}{4}\,\le\,0\,\,\forall\omega\end{eqnarray}$ どうやら見えてきた(￣ー￣)ﾆﾔﾘ上の条件式において $\left(\omega\pm\frac{x-2}{2}\right)^2\,\ge\,0\,\,\forall\omega,x$ であることから問題の関数が正実関数となるxは $x^2-12x+4\,\le\,0$ を満たすことが必要十分条件ということになる。更に操作を行うと $x^2-12x+4=\left(x-6\right)^2-32=\left(\left(x-6\right)+\sqrt{32}\right)\left(\left(x-6\right)-\sqrt{32}\right)=\left(x-\left(6-\sqrt{32}\right)\right)\left(x-\left(6+\sqrt{32}\right)\right)\le0\\6+\sqrt{32}\le x\le6-\sqrt{32}\\6-\sqrt{32}\le x\le6+\sqrt{32}$ ということになり、最後の条件を満たすxのみが解の集合として存在する。 xの二次式をグラフに描いてみると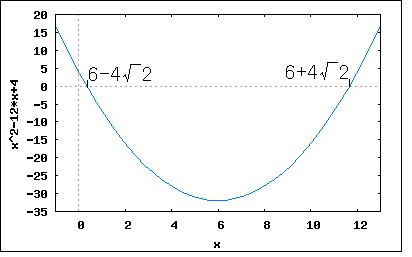従って問題の関数が正実関数となるxの範囲は $6-4\sqrt{2}\le x\le 6+4\sqrt{2}$ ということになる。なんだ簡単じゃないか(´∀` ) 確認のためにxの上下限値で問題の関数をプロットしてみると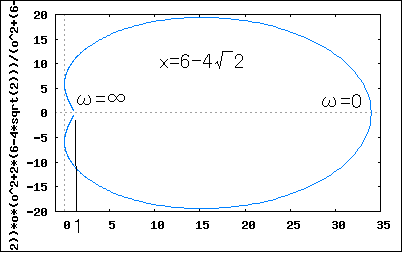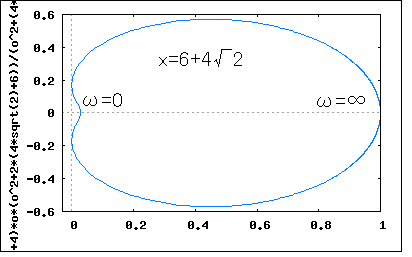どちらも右半面にのみに写像されるので正実関数であることは明らか。著者の解答よりもはるかに見通しがすっきりして満足の行く結果が得られた。 $\text{(3)}\,\,\left(\frac{s+1}{s+x}\right)^{10},\,\,tan\frac{\pi}{20}=0.158$ 最後は似たような式だが次数が10と大きい。(2)では次数は高々2次で、2次式に分解できたのですべての項を展開しても可能だったが10次となるとその限界を超えている。そろそろ一般化して扱う必要がある。 $\begin{eqnarray}\left(\frac{j\omega+1}{j\omega+x}\right)^{n}&=&\frac{\left(j\omega+1\right)^{n}}{\left(j\omega+x\right)^{n}}\\&=&\frac{\left(\omega^2+1\right)^{\frac{n}{2}}exp{j\,n\, tan^{-1}\left(\omega\right)}}{\left(\omega^2+x^2\right)^{\frac{n}{2}}exp{j\,n\, tan^{-1}\left(\frac{\omega}{x}\right)}}\\&=&\frac{\left(\omega^2+1\right)^{\frac{n}{2}}exp{j\,n\, \left(tan^{-1}\left(\omega\right)-tan^{-1}\left(\frac{\omega}{x}\right)\right)}}{\left(\omega^2+x^2\right)^{\frac{n}{2}}}\\&=&\left(\frac{\omega^2+1}{\omega^2+x^2}\right)^{\frac{n}{2}}exp{j\,n\, \left(tan^{-1}\left(\omega\right)-tan^{-1}\left(\frac{\omega}{x}\right)\right)}\\&=&\left(\frac{\omega^2+1}{\omega^2+x^2}\right)^{\frac{n}{2}}exp{j\,n\, \left(Tan^{-1}\frac{\omega-\frac{\omega}{x}}{1+\frac{\omega^2}{x}}\right)}\\&=&\left(\frac{\omega^2+1}{\omega^2+x^2}\right)^{\frac{n}{2}}exp{j\,n\, \left(Tan^{-1}\frac{\omega\left(x-1\right)}{x+\omega^2}\right)}\end{eqnarray}$ 従って問題の関数が正実関数であるためには $\begin{eqnarray}Re\left(exp{j\,n\, \left(Tan^{-1}\frac{\omega\left(x-1\right)}{x+\omega^2}\right)}\right)&=&cos(n\left(Tan^{-1}\frac{\omega\left(x-1\right)}{x+\omega^2}\right))\,\ge\,0\,\forall\omega\end{eqnarray}$ を満たす必要がある。すなわち $-\frac{\pi}{2n}\le Tan^{-1}\frac{\omega\left(1-x\right)}{x+\omega^2}\le\frac{\pi}{2n}\,\forall\omega$ ということになる。問題のケースではn=10なので、 $-\frac{\pi}{20}\le Tan^{-1}\frac{\omega\left(1-x\right)}{x+\omega^2}\le\frac{\pi}{20}\,\forall\omega$ ということになる。非常に狭い値の範囲であることが判る。条件式を3Dグラフでプロットしてみるとそのことが確認できる。条件式関数の零点であるx=1の前後限られた範囲のみが条件を満たすように見える。さて、その範囲をどうやって導出するかが問題だ。上の条件式からこの問題は以下の不等式を解く問題であることに帰着する $-tan(\frac{\pi}{20})\le \frac{\omega\left(1-x\right)}{x+\omega^2}\le tan(\frac{\pi}{20}),\,\,\forall\omega$ とりあえず最初の条件を２つの不等式に分けて各個撃破することにしよう。 $\begin{eqnarray}\frac{\omega\left(1-x\right)}{x+\omega^2}+tan(\frac{\pi}{20})&\ge& 0\\\frac{\omega\left(1-x\right)}{x+\omega^2}-tan(\frac{\pi}{20})&\le& 0\end{eqnarray}$ 最初の式の分母を払うと $\begin{eqnarray}\left(x+\omega^2\right)\left(\frac{\omega\left(1-x\right)}{x+\omega^2}+tan(\frac{\pi}{20})\right)&=&\omega\left(1-x\right)+tan(\frac{\pi}{20})\left(x+\omega^2\right)\\&=&tan(\frac{\pi}{20})\left(cot(\frac{\pi}{20})\omega\left(1-x\right)+x+\omega^2\right)\\&=&tan(\frac{\pi}{20})\left(\left(\omega+\frac{cot(\frac{\pi}{20})\left(1-x\right)}{2}\right)^2+x-\left(\frac{cot(\frac{\pi}{20})\left(1-x\right)}{2}\right)^2\right)\,\ge\,0\end{eqnarray}$ どうやら見えてきた(￣ー￣)ﾆﾔﾘ上の条件式において $\left(\omega+\frac{cot(\frac{\pi}{20})\left(1-x\right)}{2}\right)^2\,\ge\,0\,\,\forall\omega,x$ なので $x-\left(\frac{cot(\frac{\pi}{20})\left(1-x\right)}{2}\right)^2\,\ge\,0$ という条件に帰着する。xに関する二次不等式として解けば良い $\begin{eqnarray}x-\left(\frac{cot(\frac{\pi}{20})\left(1-x\right)}{2}\right)^2&=&x-\frac{cot(\frac{\pi}{20})^2\left(1-2x+x^2\right)}{4}\\&=&-\frac{cot(\frac{\pi}{20})^2}{4}\left(x^2-2\left(1+2 tan(\frac{\pi}{20})^2\right)x+1\right)\,\ge\,0\end{eqnarray}$ すなわち $\begin{eqnarray}x^2-2\left(1+2 tan(\frac{\pi}{20})^2\right)x+1\,\le\,0\end{eqnarray}$ を満たすことが必要十分条件ということになる。従って $\begin{eqnarray}x^2-2\left(1+2 tan(\frac{\pi}{20})^2\right)x+1&=&\left(x-\left(1+2 tan(\frac{\pi}{20})^2\right)\right)^2+1-\left(1+2 tan(\frac{\pi}{20})^2\right)^2\\&=&\left(x-\left(1+2 tan(\frac{\pi}{20})^2\right)+j\sqrt{1-\left(1+2 tan(\frac{\pi}{20})^2\right)^2}\right)\left(x-\left(1+2 tan(\frac{\pi}{20})^2\right)-j\sqrt{1-\left(1+2 tan(\frac{\pi}{20})^2\right)^2}\right)\\&=&\left(x-\left(1+2 tan(\frac{\pi}{20})^2\right)+\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\left(x-\left(1+2 tan(\frac{\pi}{20})^2\right)-\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\\&=&\left(x-\left(1+2 tan(\frac{\pi}{20})^2-\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\right)\left(x-\left(1+2 tan(\frac{\pi}{20})^2+\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\right)\le 0\\\\\left(1+2 tan(\frac{\pi}{20})^2-\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)&\le\,x\le& \left(1+2 tan(\frac{\pi}{20})^2+\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\\\left(1+2 tan(\frac{\pi}{20})^2+\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)&\le\,x\le& \left(1+2 tan(\frac{\pi}{20})^2-\sqrt{\left(1+2 tan(\frac{\pi}{20})^2\right)^2-1}\right)\end{eqnarray}$ という２つのケースとなる。題意よりtan(π/20)=0.158を代入すると $\begin{eqnarray}0.73&\le\,x\le& 1.37\\1.37&\le\,x\le& 0.73\end{eqnarray}$ ということになり、第一の条件を満たすxのみが解の集合として存在し第二の条件を満たすxの解の集合は存在しない（もしくは空集合しか存在しない）ことが明らか。グラフにプロットしてみるとはっきりわかる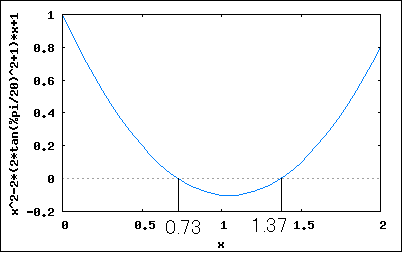従って問題の関数が正実関数となる必要十分条件は $0.73\le x\le 1.37$ ということになる。ふう始めてから１０日もかかってしまった。学生なら落第確定。独学だから納得が行くまで出来る。この問題終わり。 P.S 不等式を解くなんて学生の時以来だ。金融とか保険とかファイナンス数学では必須なんだけど工学ではめったに使わない。もしくは不等式を解かなければならない問題はめったに扱わなかったということか。今見ると集合の考え方を知っているとだいぶ見通しが良い。受験講座とかだとその当たりは曖昧にしたまま解法パターンの暗記を強要している。こういうことがことごとく数学の素養の芽を摘んでいる諸悪の根元ではなかろうか。受験数学は数学じゃないだな。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
一端子対回路：演習問題	webadm	2009-12-28 23:05
【1】複素周波数の意味	webadm	2010-1-1 20:59
【2】インピーダンス関数	webadm	2010-1-8 11:16
【3】インピーダンス関数に対する一端子対回路	webadm	2010-1-8 11:24
【4】一端子対回路のインピーダンス関数	webadm	2010-1-8 21:05
【5】インピーダンス関数の零点及び極と留数	webadm	2010-1-9 20:37
【6】正実関数、インピーダンス関数、アドミッタンス関数	webadm	2010-1-10 20:46
» 【７】正実関数	webadm	2010-3-30 9:20
【8】続：正実関数	webadm	2010-4-11 1:24
【9】続々：正実関数	webadm	2010-4-13 10:40
【10】インピーダンス関数とその回路	webadm	2010-4-15 9:49
【11】リアクタンス回路	webadm	2010-4-15 17:02
【12】続：リアクタンス回路	webadm	2010-4-15 19:39
【13】リアクタンス関数	webadm	2010-4-17 22:57
【14】相互インダクタンスを含むリアクタンス回路	webadm	2010-4-17 23:35
【15】続々：リアクタンス回路	webadm	2010-4-18 0:34
【16】リアクタンス回路の合成	webadm	2010-4-19 2:30
【17】続：リアクタンス回路の合成	webadm	2010-4-19 10:09
【18】続々：リアクタンス回路の合成	webadm	2010-4-20 4:22
【19】またまた：リアクタンス回路	webadm	2010-4-20 9:55
【20】インピーダンス関数	webadm	2010-4-21 23:11
【21】続：インピーダンス関数	webadm	2010-4-22 12:29
【22】続々：インピーダンス関数	webadm	2010-4-24 4:03
【23】またまた：インピーダンス関数	webadm	2010-4-24 11:55
【24】アドミッタンス関数	webadm	2010-4-24 20:47
【25】続：アドミッタンス関数	webadm	2010-4-27 10:19
【26】密結合変成器の分離	webadm	2010-4-28 9:20
【27】逆回路	webadm	2010-4-29 19:35
【28】続：逆回路	webadm	2010-4-30 9:49
【29】続々：逆回路	webadm	2010-4-30 10:15
【30】まだまだ：逆回路	webadm	2010-4-30 10:59
【31】もうひとつの：逆回路	webadm	2010-4-30 12:03
【32】定抵抗回路	webadm	2010-5-1 9:55
【33】続：定抵抗回路	webadm	2010-5-2 16:00

投稿するにはまず登録を