Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 一端子対回路：演習問題

投稿者	スレッド
webadm	投稿日時: 2010-4-15 9:49
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	【10】インピーダンス関数とその回路ふう、やっと正実関数が終わった。次は与えられた零点と極を持つインピーダンス関数と回路を導けというもの。ただしいずれも周波数0におけるインピーダンス値がR[Ω]とする。 (1)零点を-b、極を-aに持つ駆動点インピーダンス関数は以下の様な形となるはずである $\begin{eqnarray}Z(s)&=&H\frac{\left(s+b\right)}{\left(s+a\right)}\end{eqnarray}$ 題意よりω=0では定抵抗回路になるのでスケーリングファクターHは $\begin{eqnarray}\left.Z(s)\right\|_{s=0}&=&\left.H\frac{\left(s+b\right)}{\left(s+a\right)}\right\|_{s=0}\\&=&H\frac{b}{a}\\&=&R\\H&=&\frac{Ra}{b}\end{eqnarray}$ ということになる。したがって駆動点インピーダンス関数は $\begin{eqnarray}Z(s)&=&\frac{Ra\left(s+b\right)}{b\left(s+a\right)}\end{eqnarray}$ ということになる。回路を合成するために展開すると $\begin{eq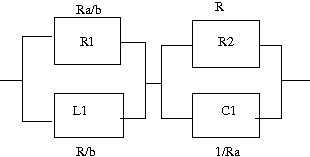narray}Z(s)&=&\frac{Ra\left(s+b\right)}{b\left(s+a\right)}\\&=&\frac{Ras}{bs+ab}+\frac{Rab}{bs+ab}\\&=&\frac{1}{\frac{1}{\Large\frac{b}{Ra}+\frac{b}{Rs}}}+\frac{1}{\Large\frac{s}{Ra}+\frac{1}{R}}\\&=&\frac{1}{\frac{1}{R_1}+\frac{1}{L_1 s}}+\frac{1}{C_1 s+\frac{1}{R_2}}\\R_1&=&\frac{Ra}{b}\,[\Omega]\\L_1&=&\frac{R}{b}\,[H]\\C_1&=&\frac{1}{R a}\,[F]\\R_2&=&R\,[\Omega]\end{eqnarray}$ 回路図を描くとということになる。著者の解答はa＞bという条件付きで誘導性インピーダンスを持つ回路となっているのに対して、こちらのはそういった制約の無い形である点が違う。元々a＞bという制約は題意には無いので、a=bやa＜bであってもよいはずだ。a=bの場合には零点と極は相殺されて消滅するので定抵抗Rとなる。a＜bの場合には、容量性インピーダンスということになる。誘導性か容量性のどちらかに決め打ちした場合には回路素子数はひとつ少なくすることができる。 (2)零点が-2a、極を-a±jbに持つ零点は実軸上で極は左半面に複素共役対で持つ。これも典型的な駆動点インピーダンス関数で表すと $\begin{eqnarray}Z(s)&=&H\frac{\left(s+2a\right)}{\left(s+a+jb\right)\left(s+a-jb\right)}\end{eqnarray}$ スケールファクタは $\begin{eqnarray}\left.Z(s)\right\|_{s=0}&=&\left.H\frac{\left(s+2a\right)}{\left(s+a+jb\right)\left(s+a-jb\right)}\right\|_{s=0}\\&=&H\frac{2a}{a^2+b^2}\\&=&R\\H&=&R\frac{a^2+b^2}{2a}\end{eqnarray}$ したがって駆動点インピーダンス関数は $\begin{eqnarray}Z(s)&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s+a+jb\right)\left(s+a-jb\right)}\end{eqnarray}$ ということになる。展開すると $begin{eqnarray}Z(s)&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s+a+jb\right)\left(s+a-jb\right)}\\&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s^2+2as+a^2+b^2\right)}\\&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s\left(s+2a\right)+a^2+b^2\right)}\\&=&\frac{1}{\frac{2a}{R\left(a^2+b^2\right)}s+\frac{2a}{R\left(s+2a\right)}}\\&=&\frac{1}{C_1 s+\frac{1}{L_1 s+R_1}}\\C_1&=&\frac{2a}{R\left(a^2+b^2\right)}\,[F]\\L_1&=&\frac{R}{2a}\,[H]\\R_1&=&R\,[\Omega]\end{eqnarray}$ ということになる。回路図で表すと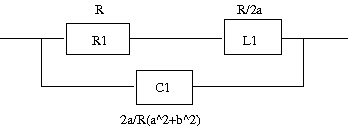ということになる。最後のは分母の式を分子の式と同じ共通項をくくりだすのがみそ。そうしないと展開結果がややこしいことになること請け合い。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
一端子対回路：演習問題	webadm	2009-12-28 23:05
【1】複素周波数の意味	webadm	2010-1-1 20:59
【2】インピーダンス関数	webadm	2010-1-8 11:16
【3】インピーダンス関数に対する一端子対回路	webadm	2010-1-8 11:24
【4】一端子対回路のインピーダンス関数	webadm	2010-1-8 21:05
【5】インピーダンス関数の零点及び極と留数	webadm	2010-1-9 20:37
【6】正実関数、インピーダンス関数、アドミッタンス関数	webadm	2010-1-10 20:46
【７】正実関数	webadm	2010-3-30 9:20
【8】続：正実関数	webadm	2010-4-11 1:24
【9】続々：正実関数	webadm	2010-4-13 10:40
» 【10】インピーダンス関数とその回路	webadm	2010-4-15 9:49
【11】リアクタンス回路	webadm	2010-4-15 17:02
【12】続：リアクタンス回路	webadm	2010-4-15 19:39
【13】リアクタンス関数	webadm	2010-4-17 22:57
【14】相互インダクタンスを含むリアクタンス回路	webadm	2010-4-17 23:35
【15】続々：リアクタンス回路	webadm	2010-4-18 0:34
【16】リアクタンス回路の合成	webadm	2010-4-19 2:30
【17】続：リアクタンス回路の合成	webadm	2010-4-19 10:09
【18】続々：リアクタンス回路の合成	webadm	2010-4-20 4:22
【19】またまた：リアクタンス回路	webadm	2010-4-20 9:55
【20】インピーダンス関数	webadm	2010-4-21 23:11
【21】続：インピーダンス関数	webadm	2010-4-22 12:29
【22】続々：インピーダンス関数	webadm	2010-4-24 4:03
【23】またまた：インピーダンス関数	webadm	2010-4-24 11:55
【24】アドミッタンス関数	webadm	2010-4-24 20:47
【25】続：アドミッタンス関数	webadm	2010-4-27 10:19
【26】密結合変成器の分離	webadm	2010-4-28 9:20
【27】逆回路	webadm	2010-4-29 19:35
【28】続：逆回路	webadm	2010-4-30 9:49
【29】続々：逆回路	webadm	2010-4-30 10:15
【30】まだまだ：逆回路	webadm	2010-4-30 10:59
【31】もうひとつの：逆回路	webadm	2010-4-30 12:03
【32】定抵抗回路	webadm	2010-5-1 9:55
【33】続：定抵抗回路	webadm	2010-5-2 16:00

投稿するにはまず登録を