| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2010-4-15 19:39 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3082 |
【12】続:リアクタンス回路 次もリアクタンス回路。
回路図で与えられたリアクタンス回路の共振及び反共振周波数を求め、その周波数特性の略図より零点と極が交互に並ぶことを示せというもの。 共振点は零点、反共振点は極に対応するので、それらが決まるとリアクタンス関数が決まる。 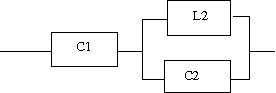 回路図から駆動点インピーダンスの式を起こすと このリアクタンス関数は零点(共振点)をω=ω1,∞、極(反共振点)をω=0,ω2に持つというのがわかる。 また0<ω1<ω2<∞という関係が成り立つので零点と極が交互に現れることを示している。 リアクタンス値をプロットしてみよう。零点は1で極は2としている。 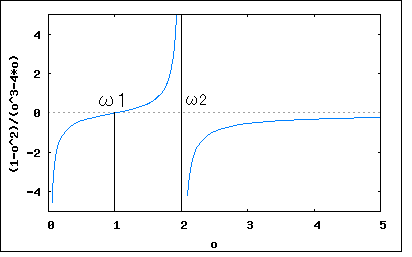 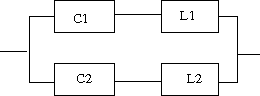 回路図から駆動点インピーダンスの式を起こすと 従って零点はω=ω1,ω3、極はω=0,ω2,∞ということになる。 0<C2L2<C1L2<∞とすれば 0<ω1<ω2<ω3<∞という関係が成り立つので零点と極は交互に現れることが明らか。 ω1=1/2,ω2=1/√2,ω3=1とした場合の周波数特性をプロットすると 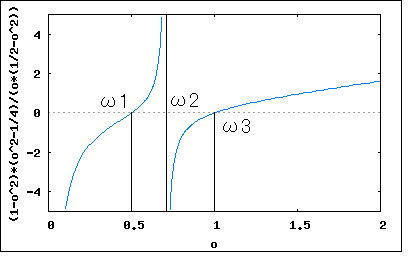 ということになる。  回路図から駆動点インピーダンスの式を起こすと 回路図から予想が付くように、C1とC2の直列合成キャパシタンスとL1とL2の並列合成インダクタンスから成るLC直列回路と等価である。 零点はω=ω1、極はω=0,∞に持つ。 C1,C2,L1,L2がそれぞれ0でなく有限値とすれば 0<ω1<∞なる関係が成り立つので零点と極は交互に現れる。 周波数特性をω1=1としてプロットしてみると。 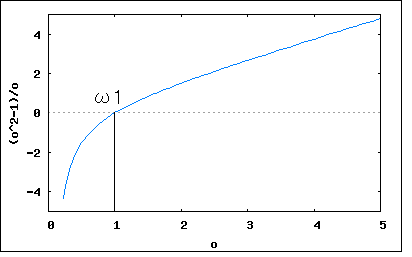 ということになる。 P.S 設問2の 0<ω1<ω2<ω3<∞ が成り立つ証明は簡単なので読者の課題としよう(´∀` ) とどのつまり以下の不等式 が0<C2L2<C1L2<∞の条件下で成り立つことを証明すればよいわけである。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

