Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 一端子対回路：演習問題

投稿者	スレッド
webadm	投稿日時: 2010-4-29 19:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3084	【27】逆回路ふう残すところあと7問。ここからしばらく逆回路の問題。以下の回路の逆回路を求めよというもの。この回路は駆動点インピーダンス関数で表すと $Z_1(s)=L_0 s$ s=0に零点、s=∞に極を持ちスケーリングファクタはL0ということになる。したがって逆回路の駆動点インピーダンス関数はs=0に極、s=∞に零点を持ちスケーリングファクタが1/L0に比例する。 $begin{eqnarray}<br />{Y_1}^\'(s)&=&Z_1(s)<br />&=&L_0 s\\<br />&=&C_0 s\\<br />C_0&=&L_0<br />\end{eqnarray}$ ということになる。回路図上ではLの双対であるCに置き換わることになる。従って逆回路の回路はとなる。次はLC直列回路駆動点インピーダンス関数は $\begin{eqnarray}<br />{Z_2}(s)&=&L_1 s+\frac{1}{C_2 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_2}^\'(s)&=&Z_2(s)\\<br />&=&L_1 s+\frac{1}{C_2 s}\\<br />&=&C_1 s+\frac{1}{L_2 s}<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 回路図的にはLがCへCがLへ、直列接続が並列接続に変わる。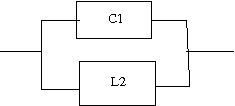次はLとLC並列回路の直列接続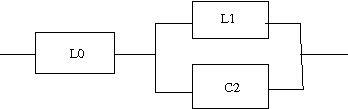駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_3(s)&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_3}^\'(s)&=&Z_3(s)\\<br />&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}\\<br />&=&C_0 s+\frac{1}{C_1 s+\frac{1}{L_2 s}}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 従ってCとLC直列回路の並列接続となる。回路図に描くと 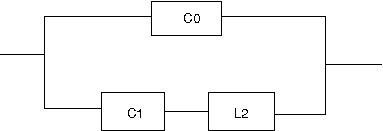s=0,∞以外にも複数の特異点を持つ場合、同じ回路が複数形存在することはFoster展開やCauer展開で学んだとおり。元の回路のインピーダンスは逆回路のアドミッタンスとなる点を利用すれば最も簡単に双対となる回路を導くことができる。次は２つのLC並列回路の直列接続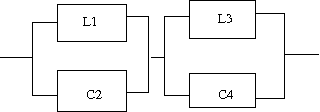関数で表すと $\begin{eqnarray}<br />Z_4(s)&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}<br />\end{eqnarray}$ 従って逆回路の関数は $\begin{eqnarray}<br />{Y_4}^\'&=&Z_4(s)\\<br />&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}\\<br />&=&\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />C_3&=&L_3\\<br />L_4&=&C_4<br />\end{eqnarray}$ ２つのLC直列回路の並列接続となる。回路図で表すと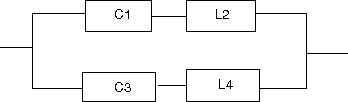最後はLとLC並列回路とCの直列接続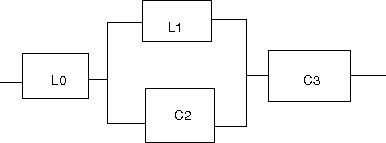駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_5(s)&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_5}^\'&=&Z_5(s)\\<br />&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}\\<br />&=&C_0 s+\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{L_3 s}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />L_3&=&C_3<br />\end{eqnarray}$ 従ってCとLC直列回路とLの並列接続となる。回路図に描くと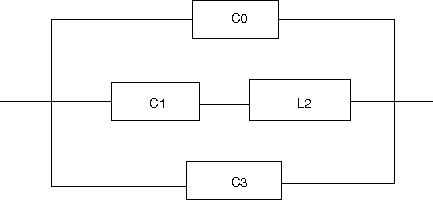ということになる。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
一端子対回路：演習問題	webadm	2009-12-28 23:05
【1】複素周波数の意味	webadm	2010-1-1 20:59
【2】インピーダンス関数	webadm	2010-1-8 11:16
【3】インピーダンス関数に対する一端子対回路	webadm	2010-1-8 11:24
【4】一端子対回路のインピーダンス関数	webadm	2010-1-8 21:05
【5】インピーダンス関数の零点及び極と留数	webadm	2010-1-9 20:37
【6】正実関数、インピーダンス関数、アドミッタンス関数	webadm	2010-1-10 20:46
【７】正実関数	webadm	2010-3-30 9:20
【8】続：正実関数	webadm	2010-4-11 1:24
【9】続々：正実関数	webadm	2010-4-13 10:40
【10】インピーダンス関数とその回路	webadm	2010-4-15 9:49
【11】リアクタンス回路	webadm	2010-4-15 17:02
【12】続：リアクタンス回路	webadm	2010-4-15 19:39
【13】リアクタンス関数	webadm	2010-4-17 22:57
【14】相互インダクタンスを含むリアクタンス回路	webadm	2010-4-17 23:35
【15】続々：リアクタンス回路	webadm	2010-4-18 0:34
【16】リアクタンス回路の合成	webadm	2010-4-19 2:30
【17】続：リアクタンス回路の合成	webadm	2010-4-19 10:09
【18】続々：リアクタンス回路の合成	webadm	2010-4-20 4:22
【19】またまた：リアクタンス回路	webadm	2010-4-20 9:55
【20】インピーダンス関数	webadm	2010-4-21 23:11
【21】続：インピーダンス関数	webadm	2010-4-22 12:29
【22】続々：インピーダンス関数	webadm	2010-4-24 4:03
【23】またまた：インピーダンス関数	webadm	2010-4-24 11:55
【24】アドミッタンス関数	webadm	2010-4-24 20:47
【25】続：アドミッタンス関数	webadm	2010-4-27 10:19
【26】密結合変成器の分離	webadm	2010-4-28 9:20
» 【27】逆回路	webadm	2010-4-29 19:35
【28】続：逆回路	webadm	2010-4-30 9:49
【29】続々：逆回路	webadm	2010-4-30 10:15
【30】まだまだ：逆回路	webadm	2010-4-30 10:59
【31】もうひとつの：逆回路	webadm	2010-4-30 12:03
【32】定抵抗回路	webadm	2010-5-1 9:55
【33】続：定抵抗回路	webadm	2010-5-2 16:00

投稿するにはまず登録を