| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2010-5-20 5:54 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
インピーダンスパラメータ &&線形受動素子のみで構成される任意の二端子対回路で一次側と二次側の電圧、電流の関係は4つのインピーダンスパラメータz11,z12,z21,z22で表すことができることを示せという問題。
基本的なことだが、実は良く解っていなかったりする。 一端子対回路の時のように一般的な電源を含まないn端子対線形受動回路網の2端子対を除いてすべて短絡したものが二端子対回路 n端子対回路のインピーダンス行列と各端子対の電圧と電流の関係を行列で表すと 証明のストラテジーとしては、I3〜Inと無関係にE1,E2,I1,I2とインピーダンス行列の関係式を導けば良いことになる。 どうすんだこれ(;´Д`) 著者の解答や他の参考書「電気回路の基礎」足立修一、森大毅共著 東京電機大学出版局をちらりと覗き見するといずれも共通して分割行列表現を使用してI3〜Inをうまい具合に消去している。偶然消去されるというのではストラテジーがなさすぎる。 意地を張って別解を考えようとすると今の季節、眠くなってすぐに寝てしまう。横になりながら考えていると、謎の定理の文章が目の前を流れていき、つかもうとしても捕まえられないというもどかしさ。記憶に残すこともできず。 とりあえずE1,E2,...,Enの単位が電圧であるとか、I1,I2,...,Inの単位が電流であるとかを一旦忘れてn次元空間の一点を表す座標と考えるとそれぞれQ(E1,E2,...,En),P(I1,I2,...,In)と表すことができる。それと原点O(0,0,...,0)とを結ぶ直線がただ一つ決まるとするとそれはn次元空間上のベクトルOQ,OPとみなすことができる。ベクトルOQがベクトルOPの間にはAなる線形変換(原点を中心とする回転と拡大縮小のスケーリング)が唯一存在することになる。 それらのn次元の点を二次元平面に投射した場合、原点OはO'に点P,Qは点P',Q'にそれぞれ投射されることになる。同様に二次元平面上のベクトルO'P'とO'Q'の間にも線形変換A'が唯一存在することになるが、その場合AとA'の間にどういう関係が成り立つかという問題に帰着する。 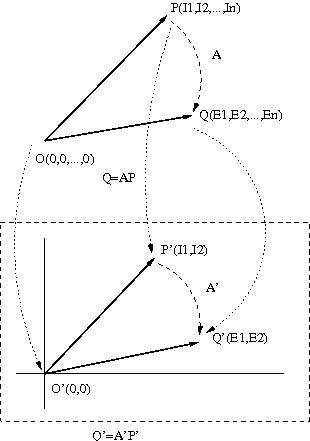 益々わからなくなってきた。よくCGやゲームで三次元オブジェクトを二次元ディスプレイ空間にレンダリングする際もこれと同じである。古くは影絵とかの伝統芸能もこうした理論が背後にある。宮本武蔵が小次郎に勝った時も船の舵で作った通常より長い木刀を小次郎の目の網膜上の二次元に投射された際に長さが実際よりも短く錯覚するような線形変換テクニックを駆使したと思われる。 よく考えたらわざわざ誰もこんな難しいこと考えないので、検索してもヒントはみつからない。意外にコンピュータグラフィックスの数理は知られていないものだということを知る。昔勉強した時に学んだ式すらどこにも見あたらない。 しかしそれも必要無いということがようやくわかった。 基本的に上の二端子対回路のモデルではI3〜Inは独立ではなくI1,I2に依存するので、E1,E2,I1,I2とインピーダンスマトリックスの関係のみ考えればよく ということになる。 ここでΔはインピーダンス行列の行列式、Δijはインピーダンス行列の余因子行列式である。 実際に上記の式に基づいてn=3やn=4のケースで計算してみると著者の方法によるものと同じ結果が得られる。 n=3のケースでは n=4のケースでは ということになる。 なんとなく暗号処理みたいに複雑で元の回路のインピーダンスマトリックス要素が配合されている。まんざら暗号処理と関係なくもなさそうである。暗号文と平文は互いに代数的な操作によって相互に変換可能である。こんなことは理数系から見ると当たり前で「ばーか、ばーか」と工学系が馬鹿にされる格好の材料でもある。これだから工学系は理数系に一生頭が上がらないのかもしれない。 P.S ううむ危うく神経衰弱になって三日三晩寝込むはめになるところだった。いきなり大きい絵を描くのは身の程知らずだったということ。 それ以前に逆行列について良くわかってなかったことも判明したり。 線形代数も今の時代色々本が出ているけど、どれもまとめに徹していて他の数学の分野とのリンクとか全然触れてないし、歴史的経緯すら触れてない。ファイナンス数理で線形代数が必須とかで売れているのかもしれない。そんなこと数学者もまったく予想してなかっただろうね。元々純粋数学だった確率微分方程式も金融工学でデリバティプ商品の値付け理論に使われてから急にスポットライトを浴びたようなものだし。 結局一番解りやすかったのは戦前のまだ線形代数とか無かった時代の高木貞治の「代数学講義」の行列と行列式の章だった。歴史的経緯からはじまるし、昔の文体は外来語がひらがなで本文は旧漢字カタカナでなかなか味わいがあってじっくり読めた(というか速読できないしこれ)。 寺澤寛一の「自然科学者のための数学概論」は行間隔や文字の大きさのバランスが絶妙にすばらしく、美しく読みやすい本であるが線形代数はおろか代数系の話しがまったくない古典解析の本でもある。それでも行列表記は随所のページに登場するが、行列そのものの理論は扱っていない。もちろん集合とかもブルバキ以前なので出てこない。行列の概念は非常にマイナーだったし、便利なのでいろいろ少しずつ多くの数学者に使われるようになって、蟻の巣穴のようにあちこちの分野とつながりだしてから、まとめて教えるということになったのだろう。しかしつながってる先を学ぶのが本来の意図なのだろうけど、数学は意図も目的も無いので無味乾燥なものとなるのは仕方がない。 いきなり最初の問題で読者の出端をくじくのが本書の常套手段だ。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2010-5-20 4:53 |
| » |
webadm | 2010-5-20 5:54 |
| |
webadm | 2010-5-22 23:43 |
| |
webadm | 2010-5-23 1:32 |
| |
webadm | 2010-5-23 10:12 |
| |
webadm | 2010-5-23 16:25 |
| |
webadm | 2010-5-23 16:33 |
| |
webadm | 2010-5-23 17:20 |
| |
webadm | 2010-5-23 17:58 |
| |
webadm | 2010-5-24 17:53 |
| |
webadm | 2010-5-26 11:41 |
| |
webadm | 2010-5-26 14:34 |
| |
webadm | 2010-5-26 15:14 |
| |
webadm | 2010-5-27 3:18 |
| |
webadm | 2010-5-27 13:50 |
| |
webadm | 2010-5-27 22:14 |
| |
webadm | 2010-5-29 3:39 |
| |
webadm | 2010-5-29 11:27 |
| |
webadm | 2010-5-29 11:57 |
| |
webadm | 2010-5-30 11:15 |
| |
webadm | 2010-5-30 12:37 |
| |
webadm | 2010-5-30 12:45 |
| |
webadm | 2010-6-3 12:42 |
| |
webadm | 2010-6-5 13:04 |
| |
webadm | 2010-6-5 13:44 |
| |
webadm | 2010-6-12 22:30 |
| |
webadm | 2010-6-13 5:07 |
| |
webadm | 2010-6-17 5:13 |
| |
webadm | 2010-6-17 16:21 |
| |
webadm | 2010-6-17 19:40 |
| |
webadm | 2010-6-22 18:50 |
| |
webadm | 2010-6-25 21:54 |
| |
webadm | 2010-6-26 0:45 |
| |
webadm | 2010-6-26 11:27 |
| |
webadm | 2010-6-26 21:55 |
| |
webadm | 2010-6-27 0:05 |
| |
webadm | 2010-6-28 21:04 |
| |
webadm | 2010-6-29 18:16 |
| |
webadm | 2010-7-8 21:06 |
| |
webadm | 2010-7-28 6:11 |
| |
webadm | 2010-8-17 10:44 |
| |
webadm | 2010-8-17 20:48 |
| |
webadm | 2010-8-18 3:42 |
| |
webadm | 2010-8-21 10:11 |
| |
webadm | 2010-10-31 3:26 |
| |
webadm | 2010-11-19 2:41 |
| |
webadm | 2010-11-23 21:29 |
| |
webadm | 2010-11-25 9:18 |
| |
webadm | 2010-11-30 0:01 |
| |
webadm | 2010-11-30 9:27 |
| |
webadm | 2010-11-30 23:28 |
| |
webadm | 2010-12-3 8:26 |
| |
webadm | 2010-12-8 9:13 |
| |
webadm | 2010-12-8 10:37 |
| |
webadm | 2010-12-9 22:51 |
| |
webadm | 2010-12-10 0:17 |
| |
webadm | 2010-12-14 6:51 |
| |
webadm | 2010-12-14 7:03 |
| |
webadm | 2010-12-20 10:10 |
| |
webadm | 2010-12-20 22:52 |
| |
webadm | 2010-12-23 13:53 |
| |
webadm | 2010-12-23 21:54 |
| |
webadm | 2011-4-22 7:02 |
| |
webadm | 2011-4-22 9:38 |
| 投稿するにはまず登録を | |

