| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-11-10 7:26 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
またひとつの:RL直列回路 次もRL直列回路の問題。
理論のときに最初に考えたモデルに立ち戻るような問題。 RL直列回路に図のような周期2T、電圧Eの方形波e(t)を加えた。(2n-1)T≦t≦2nTと2nT≦t≦(2n+1)Tにおける電流iを求めよ。またt=(2n-1)Tとt=2nTにおける電流i2n-1とi2nの比がR,L,Tの値によって定まる一定値になることを示せ。 というもの。ちなみに回路図を描いてみると、左右どちらの表現でも良い。 左はe(t)なる関数で方形波を表したもの。右はスイッチを2Tの周期で交互に切り替えるもの。 いずれにせよ電圧EをRL直列回路に加えて定常状態を待たずに1T後に電圧0を加え(短絡する)、こちらも定常状態を待たずにT後再び電圧Eに戻すを繰り返す。最初の題意は電圧E印可後から取り去るまで、取り去った後から再印可までの電流iを求めよという典型的な過渡現象解析。 題意でわかりずらいのは後の部分で、電圧が瞬時的に切り替わるタイミングでの過渡電流の比がR,L,Tで決まる一定値となることを証明せよというもの。これは電流iが解けていればそれぞれのタイミングでの電流値を求めてその比を計算してみればわかるかもしれない。 まずは電流iを解析するのが先決だ。 といっても以前にあった問題のようには簡単にはいかない気がする。 というのも以前の問題では初期状態が定常状態とその直後の過渡現象を扱うケースがほとんどだったが、この問題ではそうではない。過渡状態が繰り返すことになる。t=∞になれば過渡項は0になって挙動もほぼ同じ現象の繰り返しとなるのだろうが、t=∞になるまで計算するのは無理がある。 なんとか数学的視点から見通しよく最終的な答えを導き出せないものだろうか。工学の主目的はそこにある。 視点を変えてみると、この回路は一種のフィルタ回路である。 二端子対回路として見ると、内部にLがシリーズに一個入っていて、出力端をRで終端したものと考えることができる。Rの両端の出力電圧は回路に流れる電流i=i1=i2に比例すると考えることができる。 あるいはLとRを逆にしてもへそ曲がりだが同じ回路である。この場合、出力を終端するLの両端には電流の微分に比例した電圧が生じることになる。 あるいはもっと単純に見れば出力端を短絡した二端子対回路と見ることも出来る。 しかしこれらは複素周波数を使ったLaplace変換には都合が良いが、結局のところRL直列回路のような一階の常微分方程式のレベルではあまりありがたみがない。これらの考察は複数のエネルギーを蓄積する素子が同じ閉回路に存在する二階の常微分方程式の演習問題で再考しよう。 今朝通勤バスの中でまさに驚くべき解法を見いだした(´∀` ) t=(2n-1)Tとt=2nTに関する電流iの比率を知る必要があるのだから最初に電流iの式を得る必要があるのは確か。しかし1つの式だけで良い。というのもtをパラメータとする電流iの式が解ければどちらのタイミングの値もtを同じ式に代入すれば決定するからである。ということは式は共通の式ひとつあればいいことになる。 ならばわざわざ解を計算で求めずともよいのでは? と思ったけど甘かった。問題を解くには解決の一歩手前が見通しつけばあとはそこへ辿りつくだけのことになるのだが、そこへたどり着く道々に伏兵が潜んでいた(´Д`;) 解決の一歩手前というのは電流iを求める際には一階の非同次微分方程式の解の公式があるのでそれが該当する。伏兵が潜んでいたのは、部分積分を解決するために矩形波の導関数がどうしても必要になってくる。この段階でδ関数とかいう電気回路理論の範疇を超えた概念を持ち出すのは適切ではない。思いついたのはその方法なのだが簡単だけで現時点では封印せざるを得ない。 著者は電気回路理論で使用する数学の帰納法を使って解決の一歩手前までもってきている。くやしいがこれを真似するわけにはいかないのだ。 なんとかややこしい計算抜きで答えにたどり着けないだろうか。 とりあえず途中まで書いてしまおう。 題意のRL直列回路では以下の関係が成り立つ これは一階の非同次常微分方程式なので一般解は公式により ということになる。初期条件としてt=+0でi(+0)=0とすると ということになる。 ここで題意よりe(t)は であるからして。 従ってi2nとi2n-1の比は計算せずとも一目瞭然で ということになる。 著者は途中のi2nとi2n-1の式まではあっているが、最後にその比を求める際に誤りを犯していて、指数が(R/L)Tと正の値で振幅が時間と共に増大する(発散する)という誤った結論になってしまっている。学生の頃に古典で学んだ徒然草の「高名の木登り」を思い出した。 厳密な電流iの式については級数の収束問題を解決する必要があり、見通しの良く示すことが出来なかった。それは読者の課題としよう(´∀` ) P.S 級数の収束問題は最後の式の()内の積分項が収束するかの問題である。もし収束しないとそれに対する四則演算は意味をなさない。幸いなことに電気回路特に受動素子のみから成る線型回路網では一部の例外を除いては電流および電圧は一様収束する(与えられた時間で有界値内の値が一意的に確定する)ことが経験的にわかっているので、それを前提にして議論を進めることも可能である。しかし例外があるので(電圧や電流の値が有界値でなく不確定)その場合には注意が必要である。 著者の様に数学的帰納法を使うのが常套手段だが、それ以外に今まで学んできた数学の範疇では上巻のひずみ波とフーリエ変換で出てきた畳み込み積分なら許容範囲である。 不完全な解答のままで終わるのは忍びないので、畳み込み積分を使って()内の積分項が収束することを示すことにしよう。 と思ったもののよくよく考えたら積分の収束問題は相変わらず残ることに気づいた(;´Д`) この問題はある意味今まで通り過ぎてきた数学の歴史上の問題点に向かい合うことを余儀なくする。何が難しいかというと、電源電圧の関数e(t)が単純な等式で表すのが難しいという点にある。e(t)は有限個の不連続点(t=nTの位置)を持つため連続関数ではないが、不連続点が有限個であればRiemann積分可能である。次に難しいのはe(t)には極限値が存在しない点である。t=∞での極限値を求めようとすると不確定である。これは正弦関数や余弦関数のような超越関数と同じである。かといってFourier級数で簡単に表せるかというとそうではない。そもそも微分方程式の解がいつもy=f(x)みたいな陽関数として表されるとは限らない。この問題はそれに該当するので難しいのだ。 さて問題の難しさが判明した時点で選択肢は2つある、(1)諦める、(2)継続して考える、である。大抵の電気回路本は最初からこの種の難しい問題は華麗にスルーしてしまうので選択の余地すらない。例外的に「詳解電気回路演習」は読者にこの問題で挑戦状を突きつけている。この問題を解くには知恵が必要である。 以前に紹介した「エレガントな問題解決(The Art and Craft of Problem Solving)」には数学的な問題解決方法として、(1)結論の一歩手前の段階を見る、(2)手を動かす、(3)希望的観測、(4)簡単にする、(5)ルールを変える、など視点を柔軟にする方針が紹介されている。それと数学的帰納法、演繹法、変数変換、背理法などの数学テクニックを組み合わせて多くの問題が解けることを例示している。 i2nとi2n-1の比については結論の一歩手前を考えることによってバス通勤途中でアイデアが生まれた。しかしそのやり方は結論としては正しいが数学的には厳密に言うと間違っている。どこが間違っているかというと積分が収束しない限りそれを含む式の値が定まらないのでそれらの四則演算は不定であると言わざるを得ない。この致命的なflawを補う必要がある。それは問題の元来の難しさに立ち戻ることを意味する。 いろいろ検索で調べたり、新しく本を買い求めたりしてみたが、ずばり同じ問題を扱ったものは見あたらない。どの本の著者もこの問題を避けていると言わざるを得ない。ならばなおさら挑戦し甲斐があるというもの。 おそらく19世紀の時代にはこの問題は難問だったと言えよう。ただ一人Oliver Heavisideだけが果敢に挑戦し、正しい結果が得られる当時の数学では証明不能だった演算子法を編み出した。これは数学界への挑戦状ともなり、BromwichがHeavisideから演算子法について詳しく特性を教えてもらい、丹念に数学的に調べ上げて今日知られるラプラス変換と対応することを示した。 この問題の難しさの理由に積分(級数)の一様収束問題をあげたが、これについてWhittaker,Watson「Modern Analysys」を読むと、驚くべきことに脚注に級数の一様収束について理解が曖昧な読者はBromwich「Infinite Series」にあるOsgoodによる図解が理解を助けるだろうと推奨している。この本は出版当時にHardyも絶賛していたこともあって現在も増刷されて手に入れることができる。やはり手にいれて読んでおくべきかもしれない。 様々な困難を伴うこの問題を解決するためには、問題を簡単にするということを試していなかった。問題文そのままで取り組むと難しいが、既に知っていることや解いている問題に近づけるように簡単にすれば何か光が見えてくるかもしれない。 そこで今朝寝床で考えて思いついたのが、重ね合わせの理を使うことに立ち返るということである。そうすると視点が柔軟になり、同じ問題がもっと簡単な問題に見えてくるのが不思議だ。 それは矩形波の電圧源を以下の様に時間と極性の異なる同じステップ関数の線型結合(重ね合わせ)で置き換えることである。これは他には見られないユニークな視点である。 ステップ関数は基本的な過渡現象の最初に必ず登場するし周知のものだ。今回はそれがT時間ずつ時間シフトし、極性が交互に変わる複数(無限数)の電源が直列に接続された等価電源に置き換えることができる。ステップ状の電源電圧変化はこれまで扱ってきたので簡単そうである。あとはそれぞれの電源について解を求めて重ね合わせればできそうである。 他にもFourier級数で表すという方法も考えられるが、実数領域では三角関数の線型結合になり、複素領域では指数関数の線型結合になるのでかなりややこしい。それは読者の課題としよう(´∀` ) (2011/12/23) 大分間が開いてしまったが、その間に考えが問題から離れていたわけではなく、銀行預金が底をつきそうなのでアルバイトの仕事をしたり忙しかったのだ。仕事はやり遂げたが未だ報酬が支払われていない(;´Д`) 川崎駅のLazona内に丸善があるのを知ってそこで面白い微分方程式の本(佐藤光「微分方程式の基礎と応用」サイエンス社)を見つけたのでなけなしのお金を叩いて買って通勤途中のバスの中で読み解いていたり。過渡現象解析の理解には微分方程式に関する達観を必要とすると感じたからだ。この本は比較的ページ数は少ないが、理系で扱う応用問題に取り組めるレベルまで基礎から急勾配斜面を道案内してくれる。特に第三章までの基礎編は必要最小限のものだけを厳選して組まれており、式の誘導には適度のジャンプがあり、そのギャップを埋めるのは良い数学トレーニングになる。理解できない場合には何か基礎的な数学知識や観点が欠けていることを意味するので、それを別途学んだりすることで行間がつながるとしっかりとした理解が構築される仕組みである。おそらく第三章までは著者の長年の大学での講義の結晶であると思われる。 その先の応用については著者自身にとっても筆が進まなかったと序文に告白しているように、道は険しかったと見える。ラプラス変換へ読者を導くためには数学者としてはBromwichが辿ったように複素積分を理解しなければならないというセオリーに基づくのが無理があったのかもしれない。歴史的にはHeavisideの演算子法が先なのだがそれは数学者としてはその存在を認めるわけにはいかない。しかしそうするとLaplace変換の本来の目的、複素積分をほとんど回避して微分方程式が代数的に解く、を初期の段階で見失ってしまう。Heaviside自身はBromwichの仕事(Bromwich積分もしくは逆Laplace変換)の研究に必要な演算子法の知識を惜しみなく提供しつつも自らはBromwichが進める積分法は面倒という結論をとうの昔に出していたと思われる。やはり積分法をつかわずして高階微分方程式が解ける演算子法は当時あまりに先進的であったと言える。 今のところ第4章の複素積分の初歩で躓いていてその先の応用は斜め読みしているだけだけど、高木貞治「解析概論」の後半に出てくる特殊な解析関数(Γ関数、Bessel関数、Beta関数)は元々微分方程式の解と密接な関係があるものだと知った。「解析概論」は微分方程式論は完璧にスルーしている点で問題だと言われている理由がそれでわかった。Bessel関数は昔お世話になった社長さんが数学好きで学生の頃の物理の実験で円盤上に砂を乗せて振動を与えると一定の周波数で模様が現れるという現象を説明するために独自に微分方程式をたてて解いた結果をレポートで出したところ先生にほめられてBessel関数による解とかいろいろ教えてもらったという話しを聞かされたことがある。なるほど物理学と微分方程式はきってもきれない。そういう実験とレポートは学生の中に優れた才能を持つ人を見いだす(逆にアピールする)格好の機会なのかもしれない。と思った。 第4章以降はそれまで無かった誤植(というより明らかに原稿上のミス)が見つかった。著者は単位ステップ関数を式と文章でs(t)とU(t)と混用している。おそらくs(t)はLaplace変換のsと混同するので一般的なU(t)に修正したと思われるが、一部の式や文章で修正前のs(t)が残っていて文章と式とで矛盾が生じる残念な結果となっている。その点を除けば、理論過程のジャンプを読み手が埋める努力をしていけば最短で高度な問題への微分方程式の応用が出来る水準に到達できる良い本である。増版はされているが改訂がまだなのはその評価の高さを物語るのかもしれない。 なんの話しだったけ、ああ、重ね合わせの理を使った別解ね。 難しい問題を解くには「問題を簡単にする」というストラテジーがあるのはもうみんな知っているよね。これは相撲で言えば「自分の相撲を取る」ことは勝利につながるのと一緒。誰も自分の苦手な戦い方をしても勝てる気がしないのと同じ。数学者だったCauerはは、ナチス独裁政権下で数学で飯が食えないと工学分野の仕事で家計を支えた。その際にも苦手な工学の土俵で戦うのではなく、得意の数学の視点から工学の問題を見ることによって見事な成果を次々と生み出した。Fosterのリアクタンス関数(有理形関数)を連分数展開するとLCラダー回路が出来上がるCauerトポロジーや、楕円関数フィルター、線型受動素子回路方程式はすべてAfine変換群をなすという達観など最たるもの。 同じことはできないものの、自分の得意な土俵がどこなのか知っていれば、そこに問題を持っていくのも手である。電気回路理論を学んだのであれば重ね合わせの理を知っているので、線型受動回路であればそれが使える。回路解析は簡単になる。数学をエンジニアリングするという考えかたもある。 そこで先の複数の時間シフトした単位ステップ関数の線型結合(重ね合わせ)で問題の回路の電源を等価に置き換えた場合 という回路イメージとなる。これは以前ひずみ波で学んだ重ね合わせの理で回路を流れる電流が個々の電源単独の時に流れる電流を総和することによって得らることを意味する。 したがって という関係が成り立つ。 それぞれの電源に関する微分方程式の一般解は既に学んだ公式により ということになる。 またt=nTでin(nT)=0と初期条件を置くことによって特解は ということになる。 従ってi0(t),i1(t),i2(t),...とそれらの総和であるi(t)をそれぞれ想定してプロットしてみると、 となることが予想される。 電流は入力の変化によって立ち上がりと立ち下がりを繰り返しE/Rを上限とする範囲内に一様収束する連続関数であることが見て取れる。(n-1)TからnTまでの範囲では正則で、期間T毎に正則でない点を有するが解析接続によって全区間で連続な解析関数とみなせる。 波形は2T周期で繰り返しているように見えるが、厳密には周期関数ではない、すなわち である。 詳しくは先の問題の解答に答える形で議論しよう。 最初に危惧したように前述の重ね合わせの理で合成された電流i(t)が という交代級数で表されるため、級数の発散という疑念を解消しなければならない。プロットからそれが一様収束することが自明だが、この問題は級数の収束という数学の知識を試す意図もあるので、厳密に判定しておくべきだと思われる。 ちなみに上の式でn=0,1,2,3,4についてE=R=L=T=1としてMaximaでプロットし7てみると驚愕の事実が判明 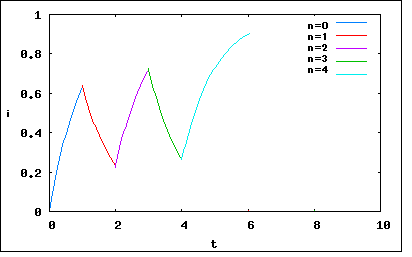 予想外に時間とともに波形が上の方へせり上がっていっていく様子がうかがえる。i(2nT)/i((2n-1)T)は予想通り1より小さいのが確認できる。 級数式を更に整理すると と書き直すことができる。 ついでに手元の回路シミュレータで同じ条件でシミュレートしてみると ほぼMaximaでプロットしたのと同じ結果であることがわかる。 先の級数式からi(2nT)、i((2n-1)T)は ということになる。 従ってi(2nT)とi((2n-1)T)の比は明白で ということになる。 できたじゃないか(´∀` ) 最後に級数が収束するかどうか確かめておこう。 手元にある昭和19年の数学古書、岡田良知「級数論」岩波書店、の"第四章 一般の級数"によれば、 引用:
とある。まさに最後のライプニッツの定理があてはまる。 従って級数は収束するので、それを含む四則演算が成立し結果は正しいということになる。 ふう、ながったよママン(ノД`) |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-11-1 17:19 |
| |
webadm | 2011-11-1 17:32 |
| |
webadm | 2011-11-3 5:24 |
| |
webadm | 2011-11-3 6:23 |
| |
webadm | 2011-11-3 8:44 |
| |
webadm | 2011-11-3 15:53 |
| |
webadm | 2011-11-3 16:32 |
| |
webadm | 2011-11-4 1:09 |
| |
webadm | 2011-11-4 2:29 |
| |
webadm | 2011-11-4 7:48 |
| |
webadm | 2011-11-5 10:47 |
| |
webadm | 2011-11-5 20:42 |
| |
webadm | 2011-11-6 1:32 |
| |
webadm | 2011-11-6 2:44 |
| |
webadm | 2011-11-6 6:17 |
| |
webadm | 2011-11-8 5:08 |
| |
webadm | 2011-11-8 7:42 |
| » |
webadm | 2011-11-10 7:26 |
| |
webadm | 2011-12-29 5:39 |
| |
webadm | 2012-1-11 8:53 |
| |
webadm | 2012-1-11 10:52 |
| |
webadm | 2012-1-14 21:44 |
| |
webadm | 2012-1-22 3:04 |
| |
webadm | 2012-1-22 23:50 |
| |
webadm | 2012-1-23 1:37 |
| |
webadm | 2012-1-23 4:15 |
| |
webadm | 2012-1-24 9:31 |
| |
webadm | 2012-1-27 7:27 |
| |
webadm | 2012-1-29 0:18 |
| |
webadm | 2012-1-29 0:45 |
| |
webadm | 2012-2-4 9:41 |
| |
webadm | 2012-2-7 6:22 |
| |
webadm | 2012-2-10 9:18 |
| |
webadm | 2012-2-12 20:06 |
| |
webadm | 2012-2-12 23:06 |
| |
webadm | 2012-2-14 7:38 |
| |
webadm | 2012-2-14 8:48 |
| |
webadm | 2012-4-5 10:59 |
| |
webadm | 2012-4-10 8:07 |
| |
webadm | 2012-4-11 15:26 |
| |
webadm | 2012-4-14 6:36 |
| |
webadm | 2012-4-14 17:43 |
| |
webadm | 2012-4-15 0:24 |
| |
webadm | 2012-4-16 3:54 |
| |
webadm | 2012-4-17 9:05 |
| |
webadm | 2012-5-5 18:09 |
| |
webadm | 2012-5-5 23:12 |
| |
webadm | 2012-5-6 19:26 |
| |
webadm | 2012-5-6 19:53 |
| |
webadm | 2012-5-6 21:41 |
| |
webadm | 2012-5-7 2:09 |
| |
webadm | 2012-5-8 8:31 |
| |
webadm | 2012-5-12 18:14 |
| |
webadm | 2012-5-13 1:37 |
| |
webadm | 2012-5-13 22:24 |
| |
webadm | 2012-5-13 23:03 |
| |
webadm | 2012-5-14 8:11 |
| |
webadm | 2012-5-19 19:10 |
| |
webadm | 2012-5-23 4:47 |
| |
webadm | 2012-5-28 23:28 |
| |
webadm | 2012-8-3 7:14 |
| |
webadm | 2012-8-4 23:52 |
| |
webadm | 2012-8-5 2:55 |
| |
webadm | 2012-8-6 21:08 |
| |
webadm | 2012-8-8 7:41 |
| |
webadm | 2012-8-8 9:30 |
| |
webadm | 2012-8-11 20:51 |
| |
webadm | 2012-8-11 22:35 |
| |
webadm | 2012-8-11 23:00 |
| |
webadm | 2012-8-12 3:28 |
| 投稿するにはまず登録を | |

