| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-11-15 11:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
Re: 自分の数学を持つことの勧め 電磁気学やベクトル解析を学ぶ上で躓きとなるのは
・電気回路理論と違い様々な物理量が次から次へと登場する ・電気回路理論の集中定数回路には距離の概念がなく、分布定数回路でやっと一次元空間だったのが、電磁気学ではいきなり3次元空間 ・数ベクトル間のスカラー積やベクトル積は少なくむしろほとどは微分演算子とベクトルの間のスカラー積やベクトル積が中心 ・多くの公式を暗記することを強いられる というところかもしれない。これで最短コースで進むとすれば落伍者が多数でてもおかしくはない。 自分でゼロから構築しなおそうとすると、よくあるテキストでは肝心要のそうした部分は割愛されていてショートカットされているのが普通であり、結論だけ辻褄が合うようになっている。 何かが隠されていると思うのは私だけではないだろう。 講義を良く聴いて内容を覚えているだけで十分ならば最終的に辻褄が合っていれば時間がかからないほうがいいのだろうけど、やはり何か秘密にされると、それを知りたいと思うのは当然である。 以前に二次元空間のベクトルの内積と外積(実際には有向面積計算)を取り上げたことがあるが、その後その続きを検討する中でおもしろい発見をしたので、ここに書いておくことにする。 教科書では内積(スカラー積)と外積(ベクトル積)は最初から別もので、その関係について詮索することはしない。というかそんな時間も無いし割くべきページ数も無いから当然である。 またベクトル解析の教科書では最初から3次元空間から始めるのが普通で、3次元空間こそ応用上重要で、それ以外は重要ではないからである。 しかし最初から3次元空間だと躓きが更に増える。 実は発見というのは、二次元で考えると内積も外積も実は一緒だということである。以前に書いた時は、二次元の外積(有向面積)は内積の片方のベクトルを90度時計方向に回転したものとの内積と同値であるということを示した。 今度は二次元では内積と外積は実は同じ形で表されるということを示すつもりだ。 行列演算の表現を借りると(本当はその必要はないのだが、そうした方が記述が短くて済むし直感的である) おさらいをすると 二次元空間(Euclid空間)上の2つのベクトルa,bの間のスカラー積(内積)とそれが作る平行四辺形の有向面積(二次元の外積)はそれぞれ ということだったが、これを前回発見した外積のとらえ方を行列演算表現で表すと ということになる。 新たな発見というのは、内積も外積も右辺は線形変換行列を間に入れた同じ形式であるということ 両者の違いは線形変換行列の成分だけだという点。 もっともこれは二次元ベクトルでの特殊性によるわけで、三次元ではまた三次元の特殊性がある。 この考えを拡張していけば、所謂テンソル(tensor)の概念の導入の枕に使えるのではないかという気がしたので書いた。 こんなことはどの教科書にも書いてないことだと思う。 おもしろいことに、正方行列をtensorの成分表現としてみなすと、ちゃんと双線形性と対称性、非対称性というのが3次元で考えるよりも遙かに判り易い利点がある。 行列演算表現にすると横向きや縦向きのベクトルが出てくるが、これは演算順序を直感的に判り易くするための幾何学的な利点を借りたものと考えたほうが良い。後でそれを確認するために、この方式を使わないで成分を辞書順に並べて考えてみることにする。 先の2つの行列演算式は成分が特定の定数を持つ線形変換行列だったが、成分の値を代数で置き換えると ということになり、どちらも同じ演算式で行列の成分値が互いに異なるということだった。行列演算表現で表すと演算の順序が縦と横の組み合わせになるので幾何学的に見て覚え易いというこということになるが、ベクトルおよび行列の成分をそれぞれ辞書順に並べてもすこし煩雑だが同じ演算を記述できる。 内積の方はクロネッカーのδと呼ばれるものが成分となっていて恒等変換行列を作る。 外積の方はエディントンのεと呼ばれるものが成分となっていて90度時計方向にベクトルを回転させる回転変換行列を作る。 本来エディントンのεは三次元以上で用いられるが、2次元で無理矢理定義してみた。 このことから、二次元の場合、内積と外積はどちらも二つのベクトルからスカラーへの線形写像(双線形写像)であり、それぞれが異なる成分から成る二階のtensor, SとTであると見なすことができる。 実は同じスカラーでも以下の様に性質が異なることがすぐに判る。 ・内積はベクトルの順序を交換しても結果は変わらない ・外積はベクトルの順序を交換すると結果の負号が変わる 内積は2つのベクトルに関して対称な演算であるが、外積はそれと異なり非対称な演算であることがわかる。 このことは3次元のベクトルで議論するとより明確になる。 この先を追記しようとしていたらWindows 7のアップデートが勝手に入ってリブートしてしまった、使用中であるにも関わらずである。以前は自動でのインストールはしないようにしたが、Windows7だとセキュリティ上重要なアップデートがあってもなんのも通知されないのな。知らずに何ヶ月も重要なアップデートを放置していたので、インストールするためにどうしても設定を変える必要があった(というか自動インストールしないでアップデートをインストールするという方法が存在しないか判らなかった)。すると今朝悲劇が起きたわけである。 なんの話だったっけ? ああ、tensorの議論の続きね。 だいぶ書いて失われてしまったのをまた書くのは気力が要る。 先の議論では以下の暗黙の了解がある ・ベクトルは直交基底の線形結合である ・内積、外積は線形写像であるので重ね合わせの理が成り立つ ベクトルは一般に一次独立な任意の基底の線形結合で表すことができるので、それを直交基底に限定しているということである。 内積と外積が線形写像であるためには、重ね合わせの理が成り立つ必要があるということである。 具体的には、以下が成り立つということになる とどのつまり、それぞれの二階のtensorの成分は ということだったわけである。 もちろんこれは二次元での特種性を含んでおり三次元では三次元の特種事情から外積に関しては別途辻褄合わせが必要になる。 三次元の場合、直交基底が3つの組になるが、内積に関しては組み合わせが増えただけで2つのベクトルをスカラーに写像することには変わらない。 一方外積は、基底が増えただけではなく、2つのベクトルからベクトルへの写像になるので話は違ってくる。 内積と外積の議論を3次元空間に拡張すると、 一応ベクトル解析の外積の規則を使うと出来ることは出来るが、線形変換行列の成分が基底ベクトルだというのが気にいらない。 これなら以下様に多くの教科書に紹介されている表現の方が簡潔であるし、ご用とお急ぎの方には好都合な暗記方法である。 しかしこれも行列の成分に基底ベクトルが含まれていて、納得が行かない。最後の式を計算するための規則を行列式の計算規則を利用して表しているだけに過ぎない。なんら新たな情報を生んではいない。 普通ならここで、何故こんなことになるのか、何か得体の知れないものが隠されているに違いないと勘ぐるのが普通である。 ここで上の表現を見て、判ったような気分になってしまうのは騙されているのである。本当に真理を知ろうとしたら、こんな欺しに乗ってはいけない。暗記しても何も本質は理解できていないのだから。 もう一度二次元から三次元に拡張した外積の式をじっと睨んでみると、 これを今度は成分別に表記すると基底は省略できるから なんと二次元の時と同じように片方のベクトルを元のベクトルと直交するベクトルに変換したものと内積をとる形になる。bから変換された3つのベクトルがそれぞれ元のベクトルbと直交していることは以下の様に簡単に確かめることができる。 実は三次元で任意のベクトルと直交する3つの相異なるベクトルを求めようとすると無数に存在するので一意的には求めることができない。 上のbと直交する3つの線形変換されたベクトルはいずれも、3つの成分のうち一つが0であるから、原点を通りそれぞれ2つの座標軸に平行で違いに直交する3つの平面に平行であることは明らかである。 幾何学的にこれを描くとどうなるのだろう 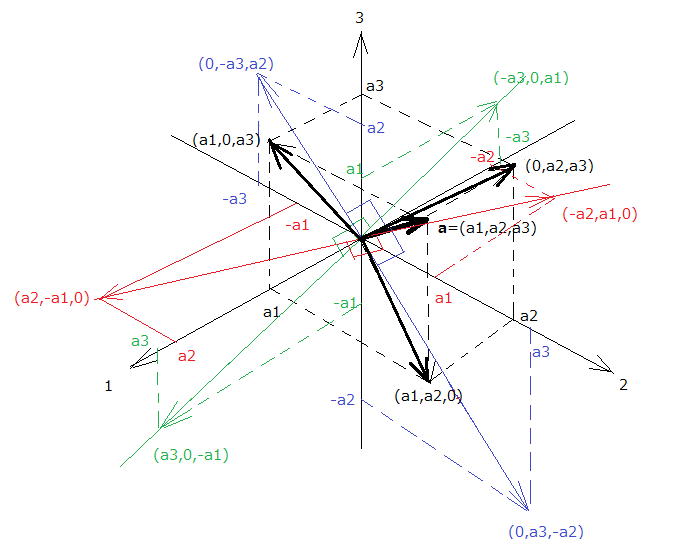 毎日通勤電車の中で毎朝毎夜この図を考え続けてきてようやく昨日アイデアがひらめいた。 先の式ではベクトルbになっているけど、図の方はbをベクトルaと読み替えてそれに直交する3組のベクトルの関係を示している。 立体的なので判り辛いけど、赤いのは座標軸1-2が張る平面上に平行なベクトルで、ベクトルaに直交するもの。緑は座標軸1-3が張る平面に平行なベクトルで、ベクトルaに直交するもの、青は座標軸2-3が張る平面に平行で、ベクトルaに直交するものをそれぞれ描いてある。 黒で描いてある(a1,a2,0), (a1,0,a3), (0,a2,a3)はそれぞれ、ベクトルaの1-2, 1-3, 2-3平面への正射影ベクトルである。 ちょうどベクトルaに直交する±(a2,-a1,0), ±(a3,0,a1), ±(0,a3,-a2)はそれぞれ(a1,a2,0), (a1,0,a3), (0,a2,a3)を同じ平面上で±90度回転したものとなっている。 ちょっと描けなかったのは、とどのつまりaに直交する3組のベクトルはaと直交し原点を通る法平面が1-2, 1-3, 2-3平面と交わる交線にそれぞれ平行であること。 紙かなんかで立体模型を作ったほうがよいかと思ったけど、切り込みが交わってしまいそうなので接着剤かメンディングテープでとめないといけないのは明らか。それは読者の課題としよう(´∀` ) こんなことはどの教科書にも書いてないけどね。こうして生きた数学的な対象と長い時間戯れるのが大事なんだよな。 ベクトルa,bとのベクトル積はベクトルaおよびbと直交するということは、両方の法平面に対して平行であるということの言い換えである。 ベクトルa, bを同じ起点に置いた場合、そのベクトル積はそれぞれの法平面が交わる交線と平行になるということである。 そして肝心のベクトルa,bの外積(ベクトル積)は、ベクトルaの3つの正射影ベクトルを90度回転したベクトルとベクトルbとの内積をそれぞれ成分とするベクトルであるということになる。これはaとbを置き換えても同じことが言える。 この議論を更に進めていく ベクトルaの法平面を考慮することは意外に重要であることが以下の事実から明らかである。 ベクトルaの法平面上に平行なベクトルの全ての集合を考える。またベクトルaとは線形独立なもうひとつのベクトルbとベクトルaの法平面に平行なベクトルの全ての集合とのベクトル積がどうなるか考えて見よう。 それは直ぐにベクトルbの法平面に平行なベクトルの全ての集合となることがわかる。何故ならベクトルbと任意の線形独立なベクトルaとのベクトル積は、ベクトルbと直交していることが必要条件であるからである。 その逆も真なりで、ベクトルbの法平面に平行なベクトル全ての集合と、ベクトルbと線形独立なベクトルaとのベクトル積は、ベクトルaの法平面に平行なベクトル全ての集合となる。 厳密な証明は読者の課題としよう(´∀` ) 従って互いに線形独立なベクトルa,bのベクトル積は、両方のベクトルの法平面に平行でなければならないから、2つの法平面の交線と平行で、それは一意的に決まると予想がつく。 二次元の時の議論で、内積というのは、片方のベクトルを平面上で90度反時計方向に回転したベクトルとの外積だった。 ということはベクトルaの法平面と1-2, 2-3, 1-3平面との交線に平行なベクトルとの内積はとどのつまり、ベクトルaの1-2, 2-3, 1-3平面への正射影ベクトルとの外積ということになる。ということは、ベクトルbとベクトルaの正射影ベクトルの外積を重ね合わせればベクトルaとbの外積と平行なベクトルが得られるのではないかという予想がつく。 実際に計算してみると、確かにそうなる これは何も不思議ではない、外積の線形性から以下の等式が成り立つことから自明な結果である 興味深いことに、3組の正射影ベクトルは互いに直交する平面に平行なため互いに線形独立だが、正射影ベクトルを元のベクトルの法平面に平行になるように90度回転したベクトルは線形独立ではない。同一平面上なので平面上のベクトルを表すのに必要な基底は2つで十分なためである。 さていよいよ議論はベクトル積の成分を生み出す源になっている線形写像行列に向かう。 前出の成分の式は行列を分解して以下の様に書き直すことが出来る。 注目すべきは、6つの線形独立な正方行列が現れていることである。 ここでテンソル積という新たな概念を導入する。新顔を入れると覚えるのが大変だけど、それまでに無いキャラを持っていれのだから役にたってくれるはず。 テンソル積は2つのテンソル(一般に階数や次元は同じである必要なない)から高階のテンソルを生成する双線形写像である。 といってもピンと来ないので、現実に生きて存在するテンソル積の例を挙げてみよう。 昔、「パンチでデート」というテレビ番組があって今もやっているかは知らないけど、一般の若い女性グループと、男性グループを公開マッチングするお見合いショーみたいなもの。見せ場は最後に番組特製のマッチングボードに男女グループが座って、それぞれが手元のボタンで相手の異性を一人だけ選ぶと、その選択がマッチングボード上で相手へ向かう線上のイルミネーションとなって現れ、互いが選択しあった相思相愛なら直線で結ばれ、そうでなければ消えるというもの。もちろんどれも気にいらなかければどれも押さなければ辞退したのと同じなので、向こう側が選択しても成立しないというわけ。いつもカップルが生まれていたわけではなく、全滅ということもよくあったので、やらせはなかったのかもしれない。 でそれとテンソル積とどういう関係があというと、男性グループをベクトルmで、女性グループをベクトルfで表すと、成立する可能性のあるカップルの組み合わせは、以下の様に表すことができる。 男女3人組の間で成立する可能性のあるカップルの組み合わせは3 x 3で9組あることになり、実際に一人の男性が複数の女性とカップルになることはできないので、各行、および各列では最大でも1組しか成立しないことになる。もちろん男女どちらかに今回は辞退ということでだれも選択をしない人が居れば、その人に関する行もしくは列は全て成立0ということになる。 もうひとつの例は、競馬のレースに出馬する馬のグループと、入賞枠の組み合わせもテンソル積で表すことができる。どの馬も入賞する可能性があるので、その組み合わせは以下の様に表すことができる。一般に入賞枠(一着、二着、三着)の数よりも出馬数の方が多く国内では8枠まである、従ってそれぞれのベクトルの次元は異なる。 公営ギャンブルでオッズの対象となるのは、このテンソル積の成分の一つ以上の組み合わせになる。また同着とならないように最後は写真判定で鼻の差で着順が争われることも珍しくない。 競馬の予想ソフトウェアを開発するには、こうした組み合わせを考える必要がある。テンソル積の概念を使えば、おもしろいかもしれない。くれぐれも本業を差し置いて、競馬にのめり込まないように願いたい。 なんの話だったっけ? ああ、テンソル積ね さてここで本題に戻って、前出のベクトル積の成分の式で現れた6つの正方行列が何かについて考えよう。 実は結論から言うと、6つの正方行列はいずれも直交基底のテンソル積である。 従ってテンソル積を使用して前出のベクトル積の成分式を書き直すと ここで更に交代積という概念を導入する。交代積はテンソル積から交代テンソルを作る線形写像で以下の様に定義される なんと交代積の成分はベクトル積と同じ成分から成る。 楔記号を使うので楔(wedge)積とも呼ばれる。テンソル積と同様に元のテンソルの階数を加えたものが生成されるテンソルの階数となる。 前出のベクトル積の成分式をwedge積を使って書き直すと ということになる。 上の式の各成分の式に現れる線形変換行列をテンソルとして一般化すると すると不思議な規則性が表れているのを発見することになる。 成分の式に現れる線形変換行列は元々は3階のテンソルだったものをスライスして二階にしたものではないかという感じがしてならない。 面倒だからどんな教科書にも書いてないけど、上の二階のテンソルと2つのベクトル(一階のテンソル)のテンソル積を計算してみると 2階のテンソルと2階のテンソルのテンソル積になるので4階のテンソルになるわけで、3階ならまだ立体的に捉えることができるけど、4階ともなると空間上ではどうにも表現できなくなる。ただ数学的には任意のn階のテンソルが出来るので、とりあえず上の様な入れ子記述にしてみた。 三次元だけでこんなに面倒になるのだから、4元空間を前提とした一般相対性理論ではそのまま成分表記していると大変なことになってしまう。今まで数学者は何をしてきたのだろうと思うけど、それを簡略する記法を考案したのがかの有名なEinsteinで、成分を全部記載する必要はないことに気付いたのは天才的である。 上の4階のテンソルはEinsteinの簡略記法を使うと以下の様に簡単に記述できる。 Einsteinの簡略記法を使うと、先のベクトル式の成分は ということになる。 これは元々三階のテンソルを2つの一階のテンソルとの内積によって、2階 rankが下がって1階のテンソルを生成するという縮約(contraction)という線形写像を意味する。 つまり、今まで線形代数とかで線形写像や行列とベクトルの積とか教わってきたのは、実はテンソルで言う縮約(もしくは縮合)というものだったということである。 なんだそういうことだったのね(´∀` ) ということでいよいよベクトル積の黒幕である謎の3階のテンソルの正体が明らかになる。 ということで謎の黒幕3階テンソルの正体は、 ということだったのね(´∀` ) まだまだおもしろい発見はあるものの、ページ文字数制限を超えそうなので、続きは後続する記事に。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| » |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

