| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-12-19 21:03 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3086 |
Re: 自分の数学を持つことの勧め ベクトル積に疑問を発してから、幾何学的な視点からそこに3階のテンソルが黒幕として潜んでいることを我々は明らかにすることができた。
とどのつまりどんな教科書にも書いてないけど、ベクトル積というのは、エディントンのεを成分とする3階のテンソルと2つの線形独立な一階のテンソル(ベクトル)のテンソル積(5階のテンソル)を1階のテンソル(ベクトル)に縮約する一種の線形写像であるということが判明した。 どの教科書にも数学書を見ても、このエディントンのεの起源については触れられていない。最初に用いたテンソル解析学を構築した数学者にちなんで Levi-Chivita 記号と呼ぶ人もいる、Eddington は Einstein の一般相対性理論の平易な解説書を書いた英国の天文学者で、おそらく彼の解説に当時ほとんど知られていなかった Levi-Chivita のテンソル解析の結果が使われて元祖よりも先に有名になったというのがありそうな話である。現在ですら Levi-Chivita の業績を調べようとしても、師匠の Ricci と共著の本を書いたことしか知りようがない。これではエディントンの名前で呼ばれても仕方がないかもしれない。 ということで大抵はそこは触れていないのだと思う。 触れてはいけないタブーにまで達してしまった感があるが、まだまだ発見は続く。 エディントンのεについては、検索すると様々な方法での定義が見つかる。しかしどれも循環論ぽいのだが( ´Д`) ひとつは直交基底のスカラー三重積による定義 ベクトル積が使われる時点で既にエディントンのεが内に潜んでいるんだが。 もうひとつはクロネッカーのδを成分とする行列式による定義 これも行列式の計算自体に既にエディントンのεが関係しているから、クロネッカーのδそのものはこじ付けだろうという気もする。 確かにクロネッカーのδとエディントンのεの間にはいくつか関係する公式が知られている。 さてエディントンのεを成分とする三階のテンソル(Eddington のテンソルもしくは Revi-Chivita テンソル)について更に調べてみることにする。 このテンソルはテンソル積で生成することが出来るのだろうか? エディントンのテンソルがベクトル積のや行列式の黒幕であることは判ったが、エディントンのテンソルの起源は依然として謎のままである。 またエディントンのテンソルをスライスすると三枚に下ろすことが出来て、それらは相異なる基底同士の交代積(2階の交代テンソル)になることは明らか。 そう考えると、エディントンのテンソルは、3つの基底の交代積(3階のテンソル)ではないかという予想されるが、それは確かだろうか? しかしながら2つのベクトルの交代積は既に定義した形で与えられるが、3つの線形独立なベクトルの交代積を考えようとすると躓いてしまう。 最近出版された本を見るとそこには交代積は登場せず、交代積の記号はベクトル積の記号として使われていてちょっと違和感を感じたが、エディントンのεを三階の交代テンソルとして登場させればそれ以上深い議論は不要なわけで、交代積すら必要ないのだと理解できる。ただしそれは余計な深みに入ってしまうことを回避するための方便とも理解できる。 古いテンソル解析の数学書を見ると、厳密にこつこつと地固めするアプローチでテンソル解析が構築されていく。そのため議論は多局面に渡るため紙面数が半端ではない。薄い本であるが、それだけに最初から凝縮する必要があり、登場する式も立てた際の意図は隠されて結果だけが示されている。意図が分からないと結果だけ示されても何のことか判らないので、それは読み手の課題ということになる。 古い数学書では当然ながらエディントンのεは出てこない。出してしまうと議論がせっかくの構成が台無しになってしまうからだろう。その代わりsgn(シグナム)という記号が登場する。 エディントンのεの場合には、3階のテンソルだから、添え字は3種類あって、その組み合わせで、成分が1, -1, 0 のいずれかになるパターンは暗記しようと思えばできるけど、どうも記憶が怪しくなると間違える可能性もある。 sgnを使用するとその可能性はだいぶ減るし、エディントンのεの解説でよく使われる添え字の偶(even)置換や奇(odd)置換というのもはっきり判る。 sgnが使用されるのは、あらかじめ1から3までの整数の数列があって、それを3つ組み合わせた全ての集合を考え、その集合の任意の要素をσとした場合、3桁の数値の異なる2桁を置換する操作を考える。この置換操作は3桁あれば3通り存在する。そうした置換された結果に対してまた同様の置換を行う、それを繰り返すと、最終的には最初に考えた集合の全体が生み出されることになる。それを図に表すとよく判る 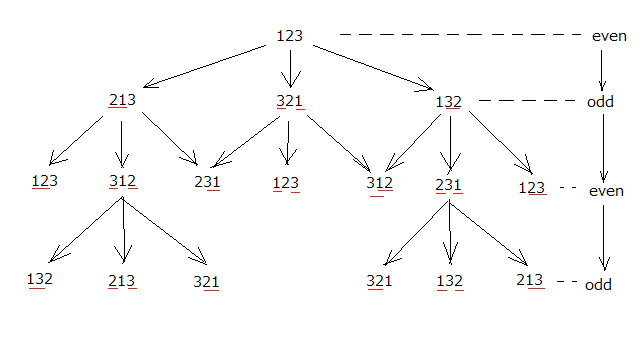 最初の組を偶(even)とすると、それに対して置換を行うと奇(odd)置換のグループが現れる、奇置換のグループに対して更に置換を行うと偶(even)置換のグループになるという具合。これを知っていれば、123が偶だとすれば奇置換のグループは直ぐに出てくるし、更に置換すれば偶のグループが出てくる。3桁の組み合わせは全部で3!=6通りあるので、これが全員集合とうことになる。 数学書ではこんな図は出てこない。 数学書では上の集合の任意の要素σとするとそれを引数としてσが偶置換か奇置換かによって1か-1を返す関数 sgn(σ)を導入している。偶置換でも奇置換でもない3桁の組み合わせ(同じ数字が2つ以上現れるもの)は元々集合にないので、0ということに。 またσ自身に引数を渡すと、指定された位置の数値を返すとすると、σ=123の場合、σ(1)=1, σ(2)=2, σ(3)=3 ということになる。 これをテンソル積の置換を表すのに使用してみると sgnとσを使用するとn階の交代積を以下の様に表せそうな予想がつく 証明は読者の課題としよう(´∀` ) テンソル代数の適当な数学専門書には大抵書いてあるはず。 既に知っている2つの1階のテンソルから二階の交代テンソルを作る交代積に関しては添え字が2種類しかないので、上の偶置換と奇置換はそれぞれひとつづつしか無いので簡単である。 ただこれは二階のテンソルの特種性に依るので、そのまま3階の交代積には通用しない面がある。 交代テンソルの定義をちゃんと考える必要がある。 2階の交代テンソルの成分は以下の関係があると言える それでは3階の交代テンソルの成分はどうなるのだろうか? 無理矢理予想すれば以下の様になると思われる なんと線形独立な成分はひとつだけで、0以外の成分は互いに符号が異なるだけということになる。 数学書ではこれをn階まで議論することなく、最初から一般のn階の交代積の成分をひとつの式で表すことになる。 この予想に従うと3階の交代積は以下の様に定義できると予想される。 テンソル積の順序が偶置換の3階のテンソルは正のsgnで奇置換の3階テンソルは負のsgnで係数倍されるとすれば簡単で判りやすい。この方法は2階の交代積にも適用できる。 テンソルを扱う教科書では上の結果しか書かれていないし、以下の様に交代積の結合則を使って展開しても最後にやっぱり3階の交代積が残るのでどうしようもなくなる。 ここまでは間違ってはいないが(交代積の場合は結合則が成り立つので)、この先どうすんだこれ( ´Д`)と躓いてしまうのがオチである。 ひどい教科書になると、この後間違った展開例をわざと例示して、ばーかばーかと言って先の正解だけ示して終わっているものもある。 さて先の予想が正しいかどうか証明抜きで、計算で確かめてみることにしよう。証明は読者の課題としよう(´∀` ) 3階のテンソルの成分は27個もあるのでこれから先現れる怪物のような式を恐れない覚悟が必要である。 上のa,b,cを一般の一階のテンソルとすると、その3階の交代積は ということになる。 どうやら予想は的中しそうな感じである。 これを元に以下の正規直交基底に関する3階の交代積を計算してみると 従って先の結果に、a1=b2=c3=1, a2=a3=b1=b3=c1=c2=0を代入すれば良く なので ということになる。 これはエディントンのεを成分とする3階の交代テンソルそのものである。 不思議なことにこの事実は手元のテンソル解析の参考書にはまったく触れられていない。自明なことだからだろうか? ということでエディントンのεの正体は正規直交基底の交代積だったということだった。ちょっと胸がすっきりした感じがする。 3次元の場合には4階以上の交代積の成分はかならず重複した添え字が伴うので全成分が0という零テンソルしか存在しないことになる。これは3次元の場合には最大でも3階のテンソルだけ考えればいいことになる。相対性理論とかでは時空間を扱うので4次元となり、4階のテンソルまで意味を持つことになる。4次元の4階のテンソルの成分は256個もあるので、Einsteinは必然的に総和記号を省略する記法を編み出さざるを得なかった。ゆくゆくは古典物理学のひとつの到達点である相対性理論をかじるためにもテンソルもかじっておいた方がよい。というかかじってないと理解できないし。 この後ちょうど良いタイミングなので、後続して正射影ベクトルを一般の基底(直交でもなく正規化されているわけでもないが、互いに線形独立なベクトル)として、一般のテンソルについて議論してみることにする。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| » |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

