Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > フィルタ演習問題

投稿者	スレッド
webadm	投稿日時: 2011-7-28 20:30
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3107	定K形高域フィルタの設計次も定K形フィルタの問題。今度は高域フィルタね。公称インピーダンスR=600[Ω],遮断周波数fh=60[kHz]の定K形高域フィルタを作り、その減衰特性、位相特性を示せ。というもの。定K形の低域フィルタと高域フィルタというのは数学的には同形。遮断周波数を中心にして周波数特性の座標軸の0と∞を逆にする変数変換で単射かつ全射な関係。減衰量を複素周波数sの関数とするなら、変数sを1/sにすると0が∞になるし∞が0になるので低域フィルタが高域フィルタになる。低域フィルタのZ1=Ls,Z2=1/Csが高域フィルタではZ1=1/Cs,Z2=Lsとなることで、Z1/2=1/2Cs,2Z2=2Lsへと変わる。遮断周波数は影像インピーダンスの式のZ1,Z2を高域フィルタのそれで置き換えると $\begin{eqnarray}<br />Z_{i1}&=&R\sqrt{\frac{Z_1}{4 Z_2}+1}=R\sqrt{\frac{\frac{1}{C s}}{4 L s}+1}=R\sqrt{\frac{1}{4 L C s^2}+1}\\<br />&=&R\sqrt{\frac{1}{4 L C}\left(4 L C-\frac{1}{\omega^2}\right)}\\<br />Z_{i2}&=&\frac{R}{\sqrt{\frac{Z_1}{4 Z_2}+1}}=\frac{R}{\sqrt{\frac{\frac{1}{C s}}{4 L s}+1}}=R\frac{R}{\sqrt{\frac{1}{4 L C s^2}+1}}\\<br />&=&\frac{R}{\sqrt{\frac{1}{4 L C}\left(4 L C-\frac{1}{\omega^2}\right)}}<br />\end{eqnarray}$ ということになる。従って影像インピーダンスが実数と純虚数の境界をとる遮断周波数fhは $\begin{eqnarray}<br />4 L C-\frac{1}{\omega^2}&=&0\\<br />\omega&=&\frac{1}{2\sqrt{L C}}=\omega_0\\<br />f_h&=&\frac{\omega_0}{2\pi}=\frac{\frac{1}{2\sqrt{L C}}}{2\pi}\\<br />&=&\frac{1}{4\pi\sqrt{L C}}<br />\end{eqnarray}$ ということになる。従って素子定数は $\begin{eqnarray}<br />\frac{Z_1}{\cancel{2}}\cancel{2} Z_2&=&Z_1 Z_2=\frac{1}{C \cancel{s}}L \cancel{s}=\frac{L}{C}=R^2=600^2\\<br />f_h&=&\frac{1}{4\pi\sqrt{L C}}=60000<br />\end{eqnarray}$ これをL,Cに関して解くと $\begin{eqnarray}<br />L&=&\frac{1}{400\,\pi }=7.96\cdot 10^{-4}=0.796[mH]\\<br />C&=&\frac{1}{144000000\,\pi }=2.21\cdot 10^{-9}=0.00221[\mu F]<br />\end{eqnarray}$ ということになる。周波数特性は減衰量が丁度低域フィルタでのω/ω0がω0/ωと逆数に置き換えた形になることから $\begin{eqnarray}<br />\theta&=&ln\left(\sqrt{A D}+\sqrt{B C}\right)=ln\left(\sqrt{1-\frac{\omega_0^2}{\omega^2}}+j\frac{\omega_0}{\omega}\right)\\<br />&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right)+j\,tan^{-1}\infty\,\,\left(\omega\le\omega_0\right)\\<br />&=&\frac{ln\left(1\right)}{2}+j\,tan^{-1}\frac{\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ 従って減衰定数及び位相定数は２つの解の集合から成り $\begin{eqnarray}<br />\alpha&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega}-1}+\frac{\omega_0}{\omega}\right),\,\,\beta=\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)\\<br />\alpha&=&0,\,\,\beta=tan^{-1}\frac{\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}=tan^{-1}\frac{1}{\sqrt{\frac{\omega^2}{\omega_0^2}-1}}\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ ということになる。む、著者の解とで位相定数の極性が異なっている。他の国内の古い参考書でも著者の解と同じく位相は負の値をとっている。Valkenburgの著書ではT字形回路だが位相は正の値をとっている点で真っ向から対立する。どっちなんだ。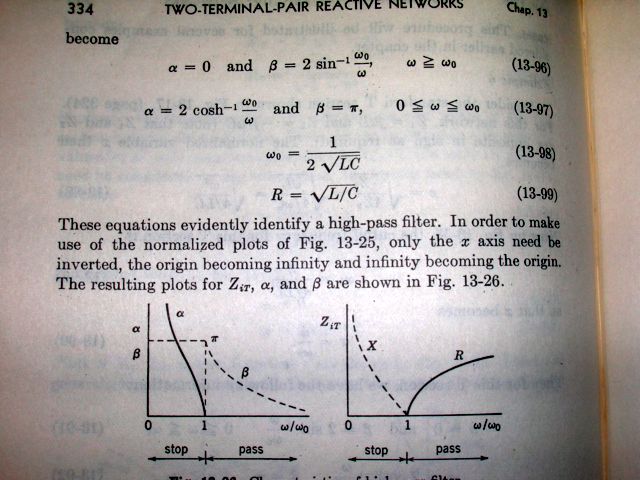国内の古い参考書はまったくといって同じやり方で定K形高域フィルタの位相定数の極性を判定している（「第一級無線技術士用　電気回路（下巻）」室住　熊三著）どうやらこちらの影像伝達定数の導出に問題があるようだ。 $\begin{eqnarray}<br />e^{\theta}&=&\sqrt{A D}+\sqrt{B C}=\sqrt{\frac{Z_1}{4\,Z_2}+1}+\sqrt{\frac{Z_1}{2}\left(\frac{1}{2\,Z_2}\right)}\\<br />&=&\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}\\<br />e^{-\theta}&=&\frac{1}{\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}}=\frac{\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}}{\left(\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}\right)\left(\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}\right)}\\<br />&=&\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}\\<br />cosh\theta&=&\frac{e^{\theta}+e^{-\theta}}{2}=\sqrt{\frac{Z_1^2}{4 R^2}+1}=\sqrt{1-\frac{1}{4 \omega^2 C^2 R^2}}\\<br />&=&\sqrt{1-\frac{1}{4 C\cancel{^2} \frac{L}{\cancel{C}}}}=\sqrt{1-\frac{1}{4 \omega^2 L C}}\\<br />&=&\sqrt{1-\frac{\omega_0^2}{\omega^2}}\\<br />sinh\theta&=&\frac{e^{\theta}-e^{-\theta}}{2}=\sqrt{\frac{Z_1^2}{4 R^2}}=\frac{Z_1}{2 R}=\frac{\frac{1}{j\omega C}}{2 \sqrt{\frac{L}{C}}}\\<br />&=&-j\fra{1}{2\omega \sqrt{L C}}\\<br />&=&-j\frac{\omega_0}{\omega}<br />\end{eqnarray}$ βが負の値としている教科書では上のように導出している。sinhθが負の純虚数を取ることが重要だ。こんな導出の手順の違いだけで結果が大きく違ってしまう。Valkenburgも弘法も筆の誤りで半世紀前に同じミスを犯している。人のことは言えないが。これで減衰定数と位相定数を導き直すと $\begin{eqnarray}<br />sinh\left(\alpha+j\beta\right)&=&sinh\alpha\,cos\beta+j\,cosh\alpha\,sin\beta=-j\frac{\omega_0}{\omega}\\<br />conh\alpha\,sin\beta&=&-\frac{\omega_0}{\omega}<br />\end{eqnarray}$ 従って減衰域ではcoshα>0であるのでsinβ<0でなければならない従ってβは負の値を取ることになる $\begin{eqnarray}<br />\theta&=&\alpha+j\beta\\<br />tanh\,\theta&=&\frac{sinh\,\theta}{cosh\,\theta}=\frac{sinh\left(\alpha+j\beta\right)}{cosh\left(\alpha+j\beta\right)}\\<br />&=&\frac{sinh\,\alpha\,cos\,\beta+j\,cosh\,\alpha\,sin\,\beta}{cosh\,\alpha\,cos\,\beta+j\,sinh\,\alpha\,sin\,\beta}\\<br />&=&\frac{\left(sinh\,\alpha\,cos\,\beta+j\,cosh\,\alpha\,sin\,\beta\right)\left(cosh\,\alpha\,cos\,\beta-j\,sinh\,\alpha\,sin\,\beta\right)}{\left(cosh\,\alpha\,cos\,\beta+j\,sinh\,\alpha\,sin\,\beta\right)\left(cosh\,\alpha\,cos\,\beta-j\,sinh\,\alpha\,sin\,\beta\right)}\\<br />&=&\frac{cosh\alpha \,sinh\alpha+j\,cos\beta \,sin\beta}{{sinh\alpha }^{2}\,{sin\beta }^{2}+{cosh\alpha }^{2}\,{cos\beta }^{2}}\\<br />&=&\frac{sinh\,2\alpha+j\,sin\,2\beta }{cos\,2\beta +cosh\,2\alpha }<br />\end{eqnarray}$ 減衰域では影像インピーダンスは純虚数となるためtanhθは実数となる。従ってtanhθの分子の式は実数でなければならないので虚数項は０でなければならない $\begin{eqnarray}<br />sin\,2\beta&=&0\\<br />2\beta&=&\pm\,n\pi\,\left(n=1,2,\cdots\right)\\<br />\beta&=&\pm\,\frac{n\pi}{2}\,\left(n=1,2,\cdots\right)<br />\end{eqnarray}$ 従ってβ=±π/2ということになるが、先の条件でβは負でなければならないためβ=-π/2ということになる。従って減衰域での減衰定数はcoshαから $\begin{eqnarray}<br />cosh\alpha\,sinh\beta&=&cosh\alpha\left(-1\right)=-\frac{\omega_0}{\omega}\\<br />\alpha&=&cosh^{-1}\left(-\frac{\omega_0}{\omega}\right)=cosh^{-1}\frac{\omega_0}{\omega}\\<br />\beta&=&-\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)\\<br />\end{eqnarray}$ ということになり、一方通過域では減衰定数α=0となるので位相定数は $\begin{eqnarray}<br />sinh\left(\alpha+j\beta\right)&=&sinh\alpha\,cos\beta+j\,cosh\alpha\,sin\beta=-j\frac{\omega_0}{\omega}\\<br />conh\alpha\,sin\beta&=&-\frac{\omega_0}{\omega}\\<br />sin\beta&=&-\frac{\omega_0}{\omega}\\<br />\beta&=&sin^{-1}\left(-\frac{\omega_0}{\omega}\right)=-sin^{-1}\frac{\omega_0}{\omega}\\<br />\alpha&=&0\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ というのが正解だった。古典フィルタ理論あなどるべからず。今回は日本の古い参考書を評価したい。グラフもプロットし直すとということだった。あえて最初の間違った解法は後学のために残しておこう。 P.S ちょっと納得が行かないので最初のアプローチでやり直してみたところ $\begin{eqnarray}<br />e^{\theta}&=&\sqrt{A D}+\sqrt{B C}=\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}=\frac{Z_1}{2 R}\sqrt{1+\frac{4 R^2}{Z_1^2}}+\frac{Z_1}{2 R}\\<br />&=&-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}-j\frac{\omega_0}{\omega}\\<br />&=&cosh\theta+sinh\theta\\<br />cosh\theta&=&-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}\\<br />sinh\theta&=&-j\frac{\omega_0}{\omega}\\<br />\theta&=&\alpha+j\beta=ln\left(-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}-j\frac{\omega_0}{\omega}\right)\\<br />&=&\frac{ln\left(1\right)}{2}+j\,tan^{-1}\frac{-\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}\,\,\left(\omega\ge\omega_0\right)\\<br />&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right)+j\,tan^{-1}-\infty\,\,\left(\omega\le\omega_0\right)\\<br />\alpha&=&0,\,\,\beta=-tan^{-1}\frac{1}{\sqrt{\frac{\omega^2}{\omega_0^2}-1}}\,\,\left(\omega\ge\omega_0\right)\\<br />\alpha&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right),\,\,\beta=tan^{-1}-\infty=-tan^{-1}\infty=-\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)<br />\end{eqnarray}$ ちゃんとできたじゃないか( ´∀`) べき根の中が正になるか負になるかで対数変換した結果が二通りに分岐してしまうのが混乱を招いている。最初にZ1^2/(4R^2)をべき根から出して後で記号変換するのがトリックだった。先に記号変換すると正しい結果が得られないという罠だった。これを正解としよう。 (2011/9/4) 解析接続するためにω0で２つの区間がオーバーラップするように訂正。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
フィルタ演習問題	webadm	2011-7-18 22:55
減衰量αの単位	webadm	2011-7-18 23:12
電力と電圧のdB	webadm	2011-7-18 23:53
電力比、電流比	webadm	2011-7-19 4:48
RL並列回路	webadm	2011-7-20 9:12
定K型低域フィルタの設計	webadm	2011-7-25 5:11
続：定K形低域フィルタの設計	webadm	2011-7-28 4:35
続々:定K形低域フィルタの設計	webadm	2011-7-28 8:42
» 定K形高域フィルタの設計	webadm	2011-7-28 20:30
続：定K形高域フィルタの設計	webadm	2011-7-29 8:25
定K形帯域フィルタの設計	webadm	2011-7-29 8:37
続：定K形帯域フィルタの設計	webadm	2011-7-31 0:28
対称定K形フィルタ	webadm	2011-8-6 9:22
対称π形高域フィルタ	webadm	2011-8-29 2:14
対称T形帯域フィルタ	webadm	2011-8-30 16:35
３素子フィルタ	webadm	2011-8-31 17:17
続：３素子フィルタ	webadm	2011-9-4 22:16
反定K形フィルタ？	webadm	2011-9-10 19:28
対称格子形回路	webadm	2011-9-12 4:11
対称T形低域フィルタ	webadm	2011-9-17 9:39
並列誘導M形フィルタ	webadm	2011-9-17 19:18
誘導M形フィルタへの変換	webadm	2011-9-18 0:41
誘導M形低域フィルタの設計	webadm	2011-9-18 5:37
続：誘導M形低域フィルタの設計	webadm	2011-9-18 18:57
続：誘導M形フィルタへの変換	webadm	2011-9-18 21:23
抵抗減衰器の設計	webadm	2011-9-18 22:01
続：抵抗減衰器の設計	webadm	2011-9-20 1:09
続々：抵抗減衰器の設計	webadm	2011-9-20 5:11
まだまだ：抵抗減衰器の設計	webadm	2011-9-20 6:06
対称ブリッジT形抵抗減衰器	webadm	2011-9-20 6:18

投稿するにはまず登録を