| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-8-31 17:17 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
3素子フィルタ 次の問題は初めて聞く3素子フィルタの影像インピーダンスをプロットし、遮断周波数を求めよという問題
ただしL=30[mH],C1=1[uF],C2=0.1[uF]とする。 今までの問題通り影像インピーダンスの解析問題であるのだが、定K形フィルタではなく3素子フィルタということだが、どちらも影像インピーダンスに基づいたフィルタであるのには違いない。 すでに伝送行列を求めて4端子パラメータから影像インピーダンスを導くアプローチは著者が解を示しているので、それ以外の方法でやってみよう。 影像インピーダンスは2端子対回路に共通なので、3素子回路のように素子数が少ない回路の場合には、影像インピーダンスを開放駆動点インピーダンスと短絡駆動点インピーダンスから求める方法を使ってみよう。 3素子フィルタは非対称回路なのでそれぞれの端での影像インピーダンスが異なる。Z1f,Z1s,Z2f,Z2sをそれぞれ端子対の開放および短絡駆動点インピーダンスとすると、それぞれの端子対の影像インピーダンスZi1,Zi2は ということになる。 回路からZ1f,Z1s,Z2f,Z2sを求めて上の式に代入すると ということになる。上記の式から影像インピーダンスが実数と純虚数をとる境界点はs=0とs=∞を除いたそれぞれの影像インピーダンスの零点と極であることは自明で ということになる。 従って遮断周波数は題意の素子定数を代入すると ということになる。 影像インピーダンスを周波数fを横軸にプロットしてみると (2011/9/4) 解析接続が明確になるように表記し直した。 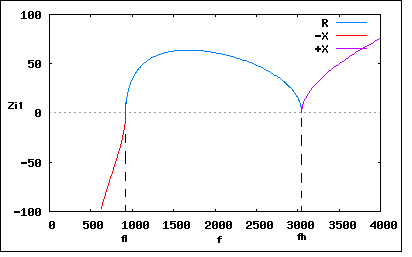 通過域ではちょっと卵の殻を半分に切ったようなカーブを描く。著者のプロットは左右対称な放物線のように描かれているが実際には対称ではない。減衰域では影像インピーダンスは純虚数をとり、同じ平面には本当は描けないが、虚数部をプロットしてみた。f<flでは容量性リアクタンス、f>fhでは誘導性リアクタンスとなり、f=0,∞に極を持つことに注意。 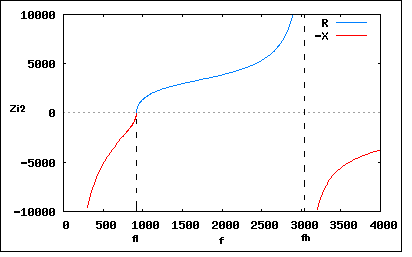 Zi2も通過域では影像インピーダンスが実数値をとり、f=flが零点でf=fhが極になる。減衰域ではともに容量性リアクタンスを取り、f=0に極を、f=∞に零点を持つ点に注意。 そういえば3素子フィルタを考案したのは誰なのだろう。この回路は逆向方向の影像インピーダンス特性はf=∞に零点を持つので高周波的にはよろしくない、どちらの方向でもf=∞に極を持つ対称T字回路にして使うのが良いだろう。そうするとシリーズに入っているLC共振回路はQの鋭い水晶発振子やセラミック共振子が使える。 これは今も随所で使われている3端子フィルタの原理そものでなかろうか。どことなく周波数特性も似ている。3素子フィルタの起源についても読者の自由研究課題としよう( ´∀`) P.S 解析接続の視点から見直して後半部分を書き改めた。影像インピーダンスの式は更に(例えばは標準化された周波数を用いて)書き直しても同じ結果が得られることを確かめるのは読者の課題としよう( ´∀`) P.S 次の問題で躓いた時にふと思い出したように開いてみたドイツの理論電気学の教科書に3素子フィルタの元ネタを偶然発見した。最初対称回路だったので気がつかなかったが、二等分すれば問題の回路と同じで3素子となる。 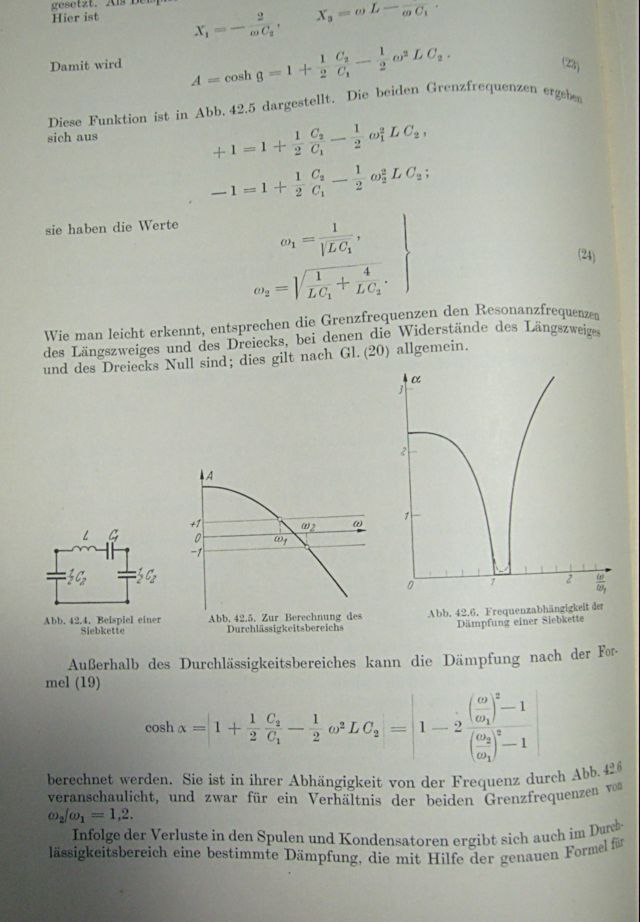 このドイツ定番テキストのすごい点は、巻末に載っている参考図書がすべてドイツ語の図書ばかり。戦前からそういう雰囲気は強かったけど、国粋主義をぷんぷん感じる。ドイツに遊学した数学者の高木貞治もそれをいやと言うほど体感したのだろう、そうした趣を批判しているが、「解析概論」ではまったく参考図書を挙げず、すべて持論であるかのようなテキストを書くという国粋主義に陥っている。当時はそういう雰囲気があったのがうらやましいと思うこともあるが、それが開戦を迎合する土壌を作ったという見方もできる。 本当に電気や電磁気学を学ぼうとする時にはドイツの理論電気学の教科書を座右に置くのも悪くないかもしれない。今も改版されて増刷されている。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-7-18 22:55 |
| |
webadm | 2011-7-18 23:12 |
| |
webadm | 2011-7-18 23:53 |
| |
webadm | 2011-7-19 4:48 |
| |
webadm | 2011-7-20 9:12 |
| |
webadm | 2011-7-25 5:11 |
| |
webadm | 2011-7-28 4:35 |
| |
webadm | 2011-7-28 8:42 |
| |
webadm | 2011-7-28 20:30 |
| |
webadm | 2011-7-29 8:25 |
| |
webadm | 2011-7-29 8:37 |
| |
webadm | 2011-7-31 0:28 |
| |
webadm | 2011-8-6 9:22 |
| |
webadm | 2011-8-29 2:14 |
| |
webadm | 2011-8-30 16:35 |
| » |
webadm | 2011-8-31 17:17 |
| |
webadm | 2011-9-4 22:16 |
| |
webadm | 2011-9-10 19:28 |
| |
webadm | 2011-9-12 4:11 |
| |
webadm | 2011-9-17 9:39 |
| |
webadm | 2011-9-17 19:18 |
| |
webadm | 2011-9-18 0:41 |
| |
webadm | 2011-9-18 5:37 |
| |
webadm | 2011-9-18 18:57 |
| |
webadm | 2011-9-18 21:23 |
| |
webadm | 2011-9-18 22:01 |
| |
webadm | 2011-9-20 1:09 |
| |
webadm | 2011-9-20 5:11 |
| |
webadm | 2011-9-20 6:06 |
| |
webadm | 2011-9-20 6:18 |
| 投稿するにはまず登録を | |

