| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-9-12 4:11 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
対称格子形回路 前問はひどかったが、今度はまともな問題。
以下の様な対称格子形回路はどのようなフィルタとなりうるかというもの。 対称格子形回路にはそれと等価な対称T形もしくは対称π形回路が存在することを二端子対回路の時にちらっと学んだ記憶がある。つまり対称二端子対回路には平衡形と非平衡形の2つのトポロジーが存在するということである。 問題の対称格子形回路と等価な開放および短絡駆動点インピーダンスを持つ以下の対称T字回路が存在すると仮定すると それぞれ回路の開放および駆動点インピーダンスが等しいことから これをZ1,Z2に関する連立方程式として解くと ということになる。後のはZ2に負の係数が伴うなので受動素子では実現できないため除外する。 これは以下の回路と等価であることを意味する 等価な対称π形回路も存在するだろうか、それを確かめるのは読者の課題としよう( ´∀`) 対称T字回路なら伝送行列も簡単に得られる。 従って影像伝達定数は ということで大変なことになったが、ω0が減衰域と通過域の境界点の周波数になるので、それが遮断周波数ということになる。 回路としては高域通過フィルタ特性を有していて、減衰域のω∞に減衰極を有する。ω2で通過域での位相定数が-π/2となる。ω∞とω2はω0を中心にω1で決まるちょうど対称位置の関係にある。 素子定数C0,C,Lをそれぞれω1<ω∞<ω0<ω2の関係を保つように決めて周波数特性をプロットしてみると あれ妙だな。ω=0が極にならない。 著者の解を見てみると、coshθの式の導出の途中で間違えていて、どう考えてもZ2+Z1をZ2*Z1として勘違いして計算しているが、偶然の誤りからω=0、ω∞に極を持つ特性の式が得られてしまっている。 引用:
これは明らかに著者のミスである。著者が流用している第二章問題【30】の結果から計算しなおしても、こちらのアプローチで得た結果と一致する。 どうすんだこれ(´Д`;) 仕方ないので、基本に戻って4端子定数の条件から直接伝送行列の要素を導いていこう。 ということになる。なんだ合ってるじゃないか( ´∀`) 以前の問題で紹介したドイツの参考書の各種フィルタ特性の一覧表のなかに、上の等価回路と同じ反回路を対称π形回路にしたものが載っている。それを見るとやはりω=0は減衰極ではなく有限値をとる。 不思議だがプロットしてみよう C=1[F],C0=10[F],L=1[H]とした場合、 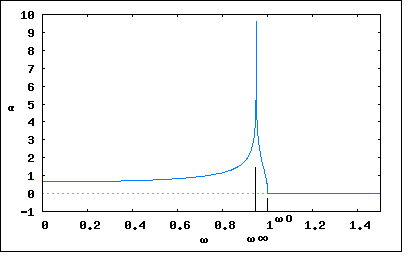 ということになる。これを正解としよう。 プロットに負のαの領域が含まれているように表示されているが、これはαの零点近傍で計算誤差が生じているためで、拡大していくとどんどん誤差は小さくなる。 これは高域フィルタと言えるのだろうか、特性的には確かにフィルタだけど。減衰量が極を除いては微々たるものだ。どちらかというとノッチフィルタに近いものがある。そういえば、対称格子形回路はブリッジ回路だった。それだ。 P.S 通勤バスに乗っている間に思い返してみたら気づいたのだが、上の等価回路はC0≧Cの場合だが、C0<Cのケースがすっぽり抜けていた。 問題の対称格子形回路はC0=0の場合は、2つのLC直列共振回路がシリーズに入った二端子対回路となる。C0が0でない場合に、C0≧Cのケースでは先の解析通りの周波数特性になるが、C0<Cの場合は状況が一変する。まず減衰定数の極ω∞が虚軸上に移る。依然としてω=0は極ではない。周波数特性はどうなるのだろう。 基本的にωが実数のみを取る以上、分母が0となることはなく極が現れないことになる。C0<Cの場合の減衰定数をプロットすると 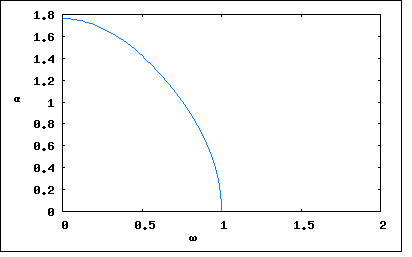 ということになる。ω0が零点であることには変わりない。 C0=Cの場合のみω=0に極を持つ。 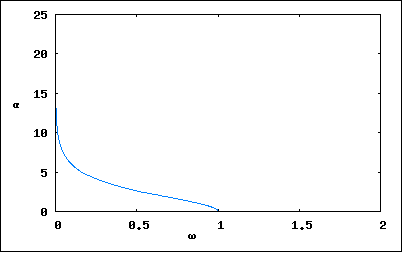 なんとも奇妙な回路である。更なる研究は読者の課題としよう( ´∀`) |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-7-18 22:55 |
| |
webadm | 2011-7-18 23:12 |
| |
webadm | 2011-7-18 23:53 |
| |
webadm | 2011-7-19 4:48 |
| |
webadm | 2011-7-20 9:12 |
| |
webadm | 2011-7-25 5:11 |
| |
webadm | 2011-7-28 4:35 |
| |
webadm | 2011-7-28 8:42 |
| |
webadm | 2011-7-28 20:30 |
| |
webadm | 2011-7-29 8:25 |
| |
webadm | 2011-7-29 8:37 |
| |
webadm | 2011-7-31 0:28 |
| |
webadm | 2011-8-6 9:22 |
| |
webadm | 2011-8-29 2:14 |
| |
webadm | 2011-8-30 16:35 |
| |
webadm | 2011-8-31 17:17 |
| |
webadm | 2011-9-4 22:16 |
| |
webadm | 2011-9-10 19:28 |
| » |
webadm | 2011-9-12 4:11 |
| |
webadm | 2011-9-17 9:39 |
| |
webadm | 2011-9-17 19:18 |
| |
webadm | 2011-9-18 0:41 |
| |
webadm | 2011-9-18 5:37 |
| |
webadm | 2011-9-18 18:57 |
| |
webadm | 2011-9-18 21:23 |
| |
webadm | 2011-9-18 22:01 |
| |
webadm | 2011-9-20 1:09 |
| |
webadm | 2011-9-20 5:11 |
| |
webadm | 2011-9-20 6:06 |
| |
webadm | 2011-9-20 6:18 |
| 投稿するにはまず登録を | |

