| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-8-23 2:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【20】ひずみ波の電力と力率 次の問題はひずみ波の電力と力率に関する問題。
電圧と電流の瞬時値が以下の式で与えられるときに有効電力と力率を求めよというもの。 e(t)=Em*sin(ωt) i(t)=Im{sin(ωt)-(1/√3)*sin(3ωt)} 電圧はひずみ波ではないが電流がひずみ波。 有効電力は瞬時値電力の平均値なので Pa=(1/T)∫e(t)*i(t)*dt =(1/T)∫(Em*sin(ωt)*Im{sin(ωt)-(1/√3)*sin(3ωt)} =(Em*Im/T)∫(sin(ωt)^2-(1/√3)sin(ωt)*sin(3ωt))dt =(Em*Im/T)*(∫sin(ωt)^2dt-(1/√3)∫sin(ωt)*sin(3ωt)dt) =(Em*Im/T)*(∫(1/2-cos(2ωt)/2)dt-(1/√3)∫(cos(-2ωt)/2-cos(4ωt)/2)dt) =(Em*Im/T)*((1/2)∫dt-(1/2)∫cos(2ωt)dt-(1/2√3)∫cos(2ωt)dt+(1/2√3∫cos(4ωt)dt) =(Em*Im*/T)*((1/2)*T) =Em*Im/2 ということになる。電圧には高調波が含まれていないので、基本波のみが有効電力に寄与する。 一方力率は有効電力と無効電力の比率なので cosφ=Pa/(|E|*|I|) =(Em*Im/2)/((1/√2)*sqrt(Em^2)*(1/√2)*sqrt(Im^2+(-Im/√3)^2)) =(Em*Im)/(Em*sqrt(Im^2+Im^2/3)) =(Em*Im)/(Em*Im*sqrt(1+1/3)) =1/sqrt(4/3) =sqrt(3/4) =√3/2 =0.866 ということになる。 |
| webadm | 投稿日時: 2009-8-23 3:33 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【21】RL直列回路とひずみ波の消費電力と力率 次は再びRL直列回路に以下のひずみ波電圧を加えた場合の消費電力と力率を求める問題。
e=200*sin(ωt+10°)+50*sin(3ωt+30°)+30*sin(5ωt+50°) 今度は覚えてしまった公式をうまく使おう。 まず基本波 e1=200*sin(ωt+10°) がRL直列回路に加えられた場合の消費電流は Pa1=|E1|*|I1|*cosφ1 ここで |E1|=Em1/√2=200/√2 |I1|=|E1|/sqrt(R^2+ω^2L^2) cosφ1=R/sqrt(R^2+ω^2L^2) 従って Pa1=((200/√2)^2/sqrt(R^2+ω^2L^2))*(R/sqrt(R^2+ω^2L^2)) =(40000*R/2)/(R^2+ω^2L^2) =20000*R/(R^2+ω^2L^2) ここで題意より R=3 [Ω] ωL=4 [Ω] を代入すると Pa1=20000*3/(3^2+4^2) =20000*3/(9+16) =20000*3/25 =2400 [W] 次に第三高調波 e3=50*sin(3ωt+30°) が加えられた場合 |E3|=Em3/√2=50/√2 |I3|=|E3|/sqrt(R^2+3^2ω^2L^2) cosφ3=R/sqrt(R^2+3^2ω^2L^2) Pa3=|E3|*|I3|*cosφ3 =((50/√2)^2/sqrt(R^2+3^2ω^2L^2))*(R/sqrt(R^2+3^2ω^2L^2)) =(50^2*R/2)/(R^2+3^2ω^2L^2) =(2500*R/2)/(R^2+3^2ω^2L^2) =1250*R/(R^2+3^2ω^2L^2) =1250*3/(3^2+3^2*4^2) =1250*3/(9+9*16) =1250*3/153 =1250/51 =24.5 [W] 第五高調波に関して e5=30*sin(5ωt+50°) |E5|=Em5/√2=30/√2 |I5|=|E5|/sqrt(R^2+5^2ω^2L^2) cosφ5=R/sqrt(R^2+5^2ω^2L^2) Pa5=|E5|*|I5|*cosφ5 =((30/√2)^2/sqrt(R^2+5^2ω^2L^2))*(R/sqrt(R^2+5^2ω^2L^2)) =(30^2*R/2)/(R^2+5^2ω^2L^2) =(900*3/2)/(3^2+5^2*4^2) =(450*3)/(9+25*16) =1350/409 =3.3 [W] 従って消費電力は Pa=Pa1+Pa3+Pa5 =2400+24.5+3.3 =2427.8 [W] ということになる。 力率は有効電力と無効電力の比なので cosφ=Pa/|E||I| =2427.8/(sqrt(|E1|^2+|E3|^2+|E5|^2)*sqrt(|I1|^2+|I3|^2+|I5|^2)) ここで |E1|=Em1/√2=200/√2 |E3|=Em3/√2=50/√2 |E5|=Em5/√2=30/√2 |I1|=|E1|/sqrt(R^2+ω^2L^2) =(200/√2)/sqrt(3^2+4^2) =(200/√2)/sqrt(9+16) =(200/√2)/sqrt(25) =(200/√2)/5 =40/√2 |I3|=|E3|/sqrt(R^2+3^2ω^2L^2) =(50/√2)/sqrt(3^2+3^2*4^2) =(50/√2)/sqrt(9+9*16) =(50/√2)/sqrt(153) |I5|=|E5|/sqrt(R^2+5^2ω^2L^2) =(30/√2)/sqrt(3^2+5^2*4^2) =(30/√2)/sqrt(9+25*16) =(30/√2)/sqrt(409) を代入すると cosφ=2427.8/(sqrt((200/√2)^2+(50/√2)^2+(30/√2)^2)*sqrt((40/√2)^2+(50/√2√153)^2+(30/√2√409)^2)) =2427.8/sqrt(40000/2+2500/2+900/2)*sqrt(1600/2+2500/2*153+900/2*409) =2427.8/sqrt(20000+1250+450)*sqrt(800+1250/153+450/409) =2427.8/sqrt(21700)*sqrt(50641700/62577) =2427.8/sqrt(21700*50641700/62577) =2427.8/4190.6 =0.579 ということになる。 |
| webadm | 投稿日時: 2009-8-24 5:52 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【22】RLC混成回路とひずみ波の電流と消費電力 次はRC直列回路とRL直列回路が並列に接続された負荷へ以下のひずみ波電圧を加えた場合の全体を流れる電流の実効値と消費電力を求める問題。
e=80√2*sin(ωt)+30√2*cos(3ωt+30°)-10√2*sin(5ωt-40°) 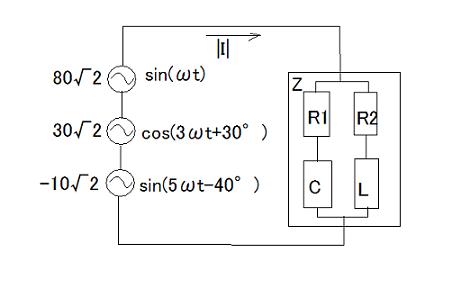 この場合負荷回路全体を合成インピーダンスZとみなして線形回路の重ね合わせによって基本波、高調波それぞれを単独電源とした場合、消費電力は Pa=|E1||I1|cosφ1+|E3||I3|cosφ3+|E5||I5|cosφ5 として求めることができる。 また同様に全体を流れる電流の実効値も基本波、高調波それぞれ単独電源とした場合に合成インピーダンスZに流れる電流の実効値から |I|=sqrt(|I1|^2+|I3|^2+|I5|^2) として求めることができる。 やってみよう。 基本波、高調波に関する電圧の実効値はそれぞれ |E1|=80√2/√2=80 [V] |E3|=30√2/√2=30 [V] |E5|=10√2/√2=10 [V] 基本波に対する合成インピーダンスは Z1=1/(1/(R1-j/ωC)+1/(R2+jωL))) =1/((R1+j/ωC)/(R1^2+(1/ωC)^2)+(R2-jωL)/(R2^2+(ωL)^2)) =1/(R1/(R1^2+(1/ωC)^2)+R2/(R2^2+(ωL)^2)+j((1/ωC)/(R1^2+(1/ωC)^2)-(ωL)/(R2^2+(ωL)^2))) 合成インピーダンスの絶対値は |Z1|=1/sqrt((R1/(R1^2+(1/ωC)^2)+R2/(R2^2+(ωL)^2))^2+((1/ωC)/(R1^2+(1/ωC)^2)-(ωL)/(R2^2+(ωL)^2))^2) =1/sqrt((5/(5^2+15^2)+10/(10^2+2^2))^2+(15/(5^2+15^2)-2/(10^2+2^2))^2) =1/sqrt((5/(25+225)+10/(100+4))^2+(15/(25+225)-2/(100+4))^2) =1/sqrt((5/250+10/104)^2+(15/250-2/104)^2) =1/sqrt((1/50+5/52)^2+(3/50-1/52)^2) =1/sqrt(((52+50*5)/(50*52))^2+((156-50)/(50*52))^2) =1/sqrt((302/2600)^2+(106/2600)^2) =1/sqrt((151/1300)^2+(53/1300)^2) =1300/sqrt(151^2+53^2) =1300/sqrt(25610) =8.123 [Ω] 従って基本波に関する電流の実効値は |I1|=|E1|/|Z1|=80/8.123=9.85 [A] 同様に各高調波についても Z3=1/(1/(R1-j/3ωC)+1/(R2+j3ωL))) =1/((R1+j/3ωC)/(R1^2+(1/3ωC)^2)+(R2-j3ωL)/(R2^2+(3ωL)^2)) =1/(R1/(R1^2+(1/3ωC)^2)+R2/(R2^2+(3ωL)^2)+j((1/3ωC)/(R1^2+(1/3ωC)^2)-(3ωL)/(R2^2+(3ωL)^2))) |Z3|=1/sqrt((R1/(R1^2+(1/3ωC)^2)+R2/(R2^2+(3ωL)^2))^2+((1/3ωC)/(R1^2+(1/3ωC)^2)-(3ωL)/(R2^2+(3ωL)^2))^2) =1/sqrt((5/(5^2+15^2/9)+10/(10^2+9*2^2))^2+((15/3)/(5^2+15^2/9)-3*2/(10^2+9*2^2))^2) =1/sqrt((5/(25+225/9)+10/(100+36))^2+(5/(25+225/9)-6/(100+36))^2) =1/sqrt((1/10+5/68)^2+(1/10-3/68)^2) =1/sqrt((68+50)/(10*68))^2+((68-30)/(10*68))^2) =1/sqrt((118/680)^2+(38/680)^2) =680/sqrt(118^1+38^2) =340/sqrt(3842) =5.48 [Ω] |I3|=|E3|/|Z3|=30/5.48=5.47 [A] Z5=1/(1/(R1-j/5ωC)+1/(R2+j5ωL))) =1/((R1+j/5ωC)/(R1^2+(1/5ωC)^2)+(R2-j5ωL)/(R2^2+(5ωL)^2)) =1/(R1/(R1^2+(1/5ωC)^2)+R2/(R2^2+(5ωL)^2)+j((1/5ωC)/(R1^2+(1/5ωC)^2)-(5ωL)/(R2^2+(5ωL)^2))) |Z5|=1/sqrt((R1/(R1^2+(1/5ωC)^2)+R2/(R2^2+(5ωL)^2))^2+((1/5ωC)/(R1^2+(1/5ωC)^2)-(5ωL)/(R2^2+(5ωL)^2))^2) =1/sqrt((5/(5^2+15^2/25)+10/(10^2+25*2^2))^2+((15/5)/(5^2+15^2/25)-5*2/(10^2+25*2^2))^2) =1/sqrt((5/(25+225/25)+10/(100+100))^2+(3/(25+225/25)-10/(100+100))^2) =1/sqrt((5/34+1/20)^2+(3/34-1/20)^2) =1/sqrt((5*20+34)/(34*20))^2+((3*20-34)/(34*20))^2) =1/sqrt(134/680)^2+(26/680)^2) =680/sqrt(134^2+26^2) =340/sqrt(4658) =4.98 [Ω] |I5|=|E5|/|Z5|=10/4.98=2.01 [A] ということになる。 従って回路全体を流れるひずみ波の電流実効値は |I|=sqrt(|I1|^2+|I3|^2+|I5|^2) =sqrt(9.85^2+5.47^2+(-2.01)^2) =11.4 [A] ということになる。 また消費電力を求めるために、基本波、高調波それぞれに対する力率を求める必要がある。それは各合成インピーダンスの偏角から cosφ1=Real(Z1)/|Z1| =((R2/(R2^2+(ωL)^2)+R1/(R1^2+(1/ωC)^2))/((R2/(R2^2+(ωL)^2)+R1/(R1^2+(1/ωC)^2))^2+((1/ωC)/(R1^2+(1/ωC)^2)-ωL/(R2^2+(ωL)^2))^2))/(1/sqrt((R1/(R1^2+(1/ωC)^2)+R2/(R2^2+(ωL)^2))^2+((1/ωC)/(R1^2+(1/ωC)^2)-(ωL)/(R2^2+(ωL)^2))^2)) =(R2/(R2^2+(ωL)^2)+R1/(R1^2+(1/ωC)^2))/sqrt((R2/(R2^2+(ωL)^2)+R1/(R1^2+(1/ωC)^2))^2+((1/ωC)/(R1^2+(1/ωC)^2)-ωL/(R2^2+(ωL)^2))^2) =(10/(10^2+2^2)+5/(5^2+15^2))/sqrt((10/(10^2+2^2)+5/(5^2+15^2))^2+(15/(5^2+15^2)-2/(10^2+2^2))^2) =(10/104+5/250)/sqrt((10/104+5/250)^2+(15/250-2/104)^2) =(151/1300)/sqrt((151/1300)^2+(53/1300)^2) =151/sqrt(151^2+53^2) =151/sqrt(25610) =0.943 cosφ3=Real(Z3)/|Z3| =((R2/(R2^2+(3ωL)^2)+R1/(R1^2+(1/3ωC)^2))/((R2/(R2^2+(3ωL)^2)+R1/(R1^2+(1/3ωC)^2))^2+((1/3ωC)/(R1^2+(1/3ωC)^2)-3ωL/(R2^2+(3ωL)^2))^2))/(1/sqrt((R1/(R1^2+(1/3ωC)^2)+R2/(R2^2+(3ωL)^2))^2+((1/3ωC)/(R1^2+(1/3ωC)^2)-(3ωL)/(R2^2+(3ωL)^2))^2)) =(R2/(R2^2+(3ωL)^2)+R1/(R1^2+(1/3ωC)^2))/sqrt((R2/(R2^2+(3ωL)^2)+R1/(R1^2+(1/3ωC)^2))^2+((1/3ωC)/(R1^2+(1/3ωC)^2)-3ωL/(R2^2+(3ωL)^2))^2) =(10/(10^2+9*2^2)+5/(5^2+15^2/9))/sqrt((10/(10^2+9*2^2)+5/(5^2+15^2/9))^2+((15/3)/(5^2+15^2/9)-3*2/(10^2+9*2^2))^2) =(10/136+5/50)/sqrt((10/136+5/50)^2+(5/50-6/136)^2) =(59/340)/sqrt((59/340)^2+(19/340)^2) =59/sqrt(59^2+19^2) =59/sqrt(3842) =0.952 cosφ5=Real(Z5)/|Z5| =((R2/(R2^2+(5ωL)^2)+R1/(R1^2+(1/5ωC)^2))/((R2/(R2^2+(5ωL)^2)+R1/(R1^2+(1/5ωC)^2))^2+((1/5ωC)/(R1^2+(1/5ωC)^2)-5ωL/(R2^2+(5ωL)^2))^2))/(1/sqrt((R1/(R1^2+(1/5ωC)^2)+R2/(R2^2+(5ωL)^2))^2+((1/5ωC)/(R1^2+(1/5ωC)^2)-(5ωL)/(R2^2+(5ωL)^2))^2)) =(R2/(R2^2+(5ωL)^2)+R1/(R1^2+(1/5ωC)^2))/sqrt((R2/(R2^2+(5ωL)^2)+R1/(R1^2+(1/5ωC)^2))^2+((1/5ωC)/(R1^2+(1/5ωC)^2)-5ωL/(R2^2+(5ωL)^2))^2) =(10/(10^2+25*2^2)+5/(5^2+15^2/25))/sqrt((10/(10^2+25*2^2)+5/(5^2+15^2/25))^2+((15/5)/(5^2+15^2/25)-5*2/(10^2+25*2^2))^2) =(10/200+5/34)/sqrt((10/200+5/34)^2+(3/34-10/200)^2) =(67/340)/sqrt((67/340)^2+(13/340)^2) =67/sqrt(67^2+13^2) =67/sqrt(4658) =0.982 ということになる。 従って消費電力は Pa=|E1||I1|cosφ1+|E3||I3|cosφ2+|E5||I5|cosφ3 =80*9.85*0.943+30*5.47*0.952+10*2.01*0.982 =919.05 [W] ということになる。 ちなみに著者は回路の複素アドミタンスを使って、複素電流値を求め、それをフェーザ表記で実効値と偏角を算出している。また電流の瞬時値の式も導いているが、電流の実効値と消費電力を求めるには必ずしもその必要はない。 また著者は力率を求める際に決定的な過ちを犯している。 合成アドミッタンスの偏角と電圧の瞬時値の位相から電流の瞬時値の位相を求めたまでは良いが、力率を電流の位相から求めているがこれは明らかな間違いである。理論のときに学んだ公式を導く過程でも、電圧の位相は電流に含まれる位相分でキャンセルされ負荷の偏角のみが有効電力を左右することになるからである。 これを証明するために、著者が導きだした電流の瞬時値の式と題意の電圧の瞬時値の式から有効電力の式を導いてみよう。 e=80√2*sin(ωt)+30√2*cos(3ωt+30°)-10√2*sin(5ωt-40°) i=9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ωt+47.8°)-2.01√2*sin(5ωt-29.1°) 瞬時値電力は p=e*i =(80√2*sin(ωt)+30√2*cos(3ωt+30°)-10√2*sin(5ωt-40°))*(9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ωt+47.8°)-2.01√2*sin(5ωt-29.1°)) =80√2*9.84√2*sin(ωt)*sin(ωt+19.4°)+30√2*5.48√2*cos(3ωt+30°)*cos(3ωt+47.8°)+10√2*2.01√2*cos(5ωt-40°)*sin(5ωt-40°)*sin(5ωt-29.1°)+80√2*sin(ωt)*(5.48√2*cos(3ωt+47.8°)-2.01√2*sin(5ωt-29.1°))+30√2*cos(3ωt+30°)*(9.84√2*sin(ωt+19.4°)-2.01√2*sin(5ωt-29.1°))-10√2*sin(5ωt-40°)*(9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ω+47.8°)) 有効電力は瞬時値電力の平均なので Pa=(1/T)∫pdt =(1/T)∫(80√2*9.84√2*sin(ωt)*sin(ωt+19.4°)+30√2*5.48√2*cos(3ωt+30°)*cos(3ωt+47.8°)+10√2*2.01√2*sin(5ωt-40°)*sin(5ωt-29.1°)+80√2*sin(ωt)*(5.48√2*cos(3ωt+47.8°)-2.01√2*sin(5ωt-29.1°))+30√2*cos(3ωt+30°)*(9.84√2*sin(ωt+19.4°)-2.01√2*sin(5ωt-29.1°))-10√2*sin(5ωt-40°)*(9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ω+47.8°)))dt =(1/T)*(80√2*9.84√2∫sin(ωt)*sin(ωt+19.4°)dt+30√2*5.48√2∫cos(3ωt+30°)*cos(3ωt+47.8°)dt+10√2*2.01√2∫sin(5ωt-40°)*sin(5ωt-29.1°)dt) =(1/T)*(80*9.84*2∫(cos(-19.4°)/2-cos(2ωt+19.4°)/2)dt+30*5.48*2∫(cos(-17.8°)/2+cos(6ωt+77.8°)/2)dt+10*2.01*2∫(cos(-10.9°)/2-cos(10ωt-69.1°)/2)dt) =80.9.84*cos(19.4°)+30*5.48*cos(17.8°)+10*2.01*cos(10.9°) =80.9.84*0.943+30*5.48*0.952+10*2.01*0.982 =918.57 [W] ということになる。著者の電流実効値とは小数点以下2桁目が違うのでこちらの計算結果にわずかな違いが出ているが基本的にはあっている。一方著者の解は明らかに間違いであることが証明された。 またこの検証過程で著者の電流の瞬時値の式操作の過程に誤りがあるのを発見したので、上記の検証ではそれは訂正したものを使用している。 著者は電流の瞬時値の式を i=9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ωt+30°+17.8°)-2.01√2*sin(5ωt-40°+10.9°) =9.84√2*sin(ωt+19.4°)+5.48√2*cos(3ωt+47.8°)-2.01*sin(5ωt-29.1°) としているが、最後に2.01√2を転記する際に√2が消えてしまっている。 また良く見ると消費電力の計算式にも転記ミスと思われるものがある。 Pa=|E1||I1|cosφ1+|E3||I3|cosφ3+|E5||I5|cosφ5 =80*9.64*cos(19.4°)+30*5.51*cos(47.8°)+10*2.01*cos(29.1°) とあるが、|I3|が5.51ということになっているが、瞬時値電流の式では5.48とあるので明らかに誤記である。 今まで見て来た中で解き方からして間違っているというのはなかったのと、転記ミスとはいえ誤記が多いのはちょっとひどすぎる。 |
| webadm | 投稿日時: 2009-8-24 11:05 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【23】方形波のFourier級数展開と波形率、波高率 次ぎは方形波をFourier級数展開しそのスペクトルと波形率、波高率を示せというもの。
波形は典型的な奇数波かつ対称波であることから奇数次の奇数波のみで構成されている。 b0=bn=0 e=A (0≦t≦T/2) =-A (T/2≦t≦T) an=(4/T)∫e*sin((2n-1)ωt)dt (0≦t≦T/2 n=1,∞) =(4/T)∫A*sin((2n-1)ωt)dt =(4*A/T)∫sin((2n-1)ωt)dt =(4*A/T)*(1/(2n-1)ω-cos(((2n-1)ωT)/2)/(2n-1)ω) ここで T=2π/ω を代入すると an=(2*A/π)*(1-cos((2n-1)π))/(2n-1) =4*A/π(2n-1) (m=0,∞) 従ってFourier級数展開は e(t)=(4*A/π)Σ(1/(2n-1))*sin((2n-1)ωt) (n=1,∞) =(4*A/π)*(sin(ωt)+(1/3)*sin(3ωt)+(1/5)*sin(5ωt)+...) ということになる。 波形率は実効値と平均値の比で定義されるので 実効値=sqrt((1/T)∫e^2dt) (0≦t≦T) =sqrt((1/T)∫A^2dt) =sqrt(A^2) =A 平均値=(2/T)∫edt (0≦t≦T/2) =(2/T)∫Adt =A 波形率=実効値/平均値 =A/A =1 一方波高率は最大値と実効値の比で定義されるので 波高率=A/A =1 スペクトルをプロットすると wxplot2d([-(2*((-1)^(2*n-1)-1))/(2*n-1)], [n,1,5], [nticks,1])$ 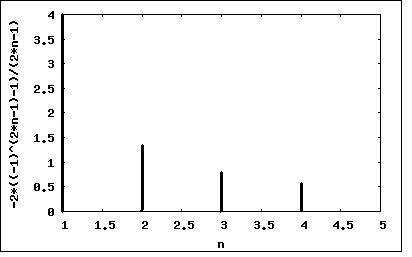 ということになる。 |
| webadm | 投稿日時: 2009-8-25 10:05 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【24】キャパシタンスに流れる電流のFourier級数展開 次ぎは以下の様な電圧波形をキャパシタンスCに加えた時に流れる電流をFourier級数により求めると供に電圧の時間微分より求めた電流と比較して一致するか確かめよというもの。
電圧波形を式で表すと e(t)=A*t/(T/2) (0≦t≦T/2) =A-A*t/(T/2) (T/2≦t≦T) これは偶関数波なので偶関数の基本波、高調波のみからなるためそのFourier級数展開は e(t)=(1/2)b0+Σbn*cos(nωt) という形になる。 従って b0=(4/T)∫e(t)dt (0≦t≦T/2) =(4/T)∫(A*t/(T/2))dt =(8*A/T^2)∫tdt =(8*A/T^2)*(T^2/8) =A bn=(4/T)∫e(t)*cos(nωt)dt (0≦t≦T/2) =(4/T)∫(A*t/(T/2))*cos(nωt)dt =(8*A/T^2)∫t*cos(nωt)dt =(8*A/T^2)*((nωT*sin(nωT/2)+2*cos(nωT/2))/2n^2ω^2-1/n^2ω^2) ここで ω=2π/T を代入すると bn=(8*A/T^2)*((2πn*sin(nπ)+2*cos(nπ))/2n^2(2π/T)^2-1/n^2(2π/T)^2) =(8*A/T^2)*(cos(nπ)-1)*T^2/4π^2n^2 =(2*A/π^2)*((-1)^2-1)/n^2 =-(4*A/π^2)/(2m+1)^2 (m=0,∞) 従って e(t)=A/2+Σ(-(4*A/π^2)/(2m+1)^2)*cos((2m+1)ωt) (m=0,∞) =A/2-(4*A/π^2)*(cos(ωt)+(1/3^2)*cos(3ωt)+(1/5^2)*cos(5ωt)+...) ということになる。 この電圧瞬時値をキャパシタンスCに加えると流れる電流は以下の回路で基本波及び高調波をそれぞれ単独で考えた場合に流れる電流の重ね合わせであるので 基本波電源に関して流れる電流は i(t)=C*d(e(t))/dt =C*d(A/2-(4*A/π^2)*(cos(ωt)+(1/3^2)*cos(3ωt)+(1/5^2)*cos(5ωt)+...))/dt =(4*A*ωC/π^2)*(sin(ωt)+(1/3)*sin(3ωt)+(1/5)*sin(5ωt)+...) ということになる。 一方電圧波形を微分して得られる電流波形は i(t)=C*d(A*t/(T/2))/dt (0≦t≦T/2) =2*A*C/T (0≦t≦T/2) =C*d(A-A*t/(T/2))/dt (T/2≦t≦T) =-2*A*C/T (T/2≦t≦T) ということになる。これは方形波で奇数波かつ対称波であるのでFourier級数展開は奇数時で奇関数の基本波と高調波からなる i(t)=Σa(2m+1)*sin((2m+1)ωt) (m=0,∞) a(2m+1)=(4/T)∫(2*A*C/T)*sin((2m+1)ωt)dt (0≦t≦T/2) =(8*A*C/T^2)∫sin(nωt)dt =(8*A*C/T^2)*(1/(2m+1)ω-cos((2m+1)ωT/2)/(2m+1)ω) ここで ω=2π/T を代入すると a(2m+1)=(8*A*C/T^2)*(1/(2m+1)*(2π/T)-cos((2m+1)*(2π/T)*T/2)/(2m+1)*(2π/T)) =(4*A*C/T)*(1/(2m+1)π-cos((2m+1)π)/(2m+1)π) =(4*A*C/πT)*(1-(-1)^(2m+1))/(2m+1) ここで T=2π/ω を代入すると an(2m+1)=(4*A*C/π(2π/ω))*(1-(-1)^(2m+1))/(2m+1) =(2*A*ωC/π^2)*(1-(-1)^(2m+1))/(2m+1) =(4*A*ωC/π^2)/(2m+1) ということになる。従ってFourier級数展開は i(t)=(4*A*ωC/π^2)Σsin((2m+1)/(2m+1) =(4*A*ωC/π^2)*(sin(ωt)+(1/3)*sin(3ωt)+(1/5)*sin(5ωt)+...) ということになる。これは先に導いた式と一致している。 |
| webadm | 投稿日時: 2009-8-25 12:59 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【25】三角波のFourier級数展開 以下の三角波をFourier級数展開し、また波形をT/4だけ左へずらしたときどうなるか示せという問題。
式で表すと e(t)=A*t/(T/4) (0≦t≦T/4) =(A-A*t/(T/4)) (T/4≦t≦3T/4) =(A*t/(T/4)-A) (3T/4≦t≦T) 波形は奇関数波かつ対称波であるので、Fourier級数展開は奇数次の基本波と高調波のみからなるので b0=bn=0 e(t)=Σa(2m+1)*sin((2m+1)ωt) a(2m+1)=(8/T)∫e(t)*sin((2m+1)ωt)dt (0≦t≦T/4) =(8/T)∫(A*t/(T/4))*sin((2m+1)ωt)dt =(32*A/T^2)∫t*sin((2m+1)ωt)dt =(32*A/T^2)*(4*sin((2m+1)ωT/4)-(2m+1)*ωT*cos((2m+1)ωT/4))/4*(2m+1)^2ω^2 ここで ω=2π/T を代入すると a(2m+1)=(32*A/T^2)*(4*sin((2m+1)*(2π/T)*T/4)-(2m+1)*(2π/T)*T*cos((2m+1)*(2π/T)*T/4))/4*(2m+1)^2*(2π/T)^2 =(2*A/π^2)*(4*sin((2m+1)π/2)-(2m+1)2π*cos((2m+1)π/2))/(2m+1)^2 =(8*A/π^2)*(-1)^m/(2m+1)^2 ということになる。従ってFourier級数展開は e(t)=(8*A/π^2)Σ((-1)^m/(2m+1)^2)*sin((2m+1)ωt) =(8*A/π^2)*(sin(ωt)-(1/3^2)*sin(3ωt)+(1/5^2)*sin(5ωt)+..) ということになる。 同様にT/4だけ左にシフトするということは e'(t)=e(t+T/4) ということになる。従ってそのFourier級数展開は e'(t)=(8*A/π^2)Σ((-1)^m/(2m+1)^2)*sin((2m+1)ω(t+T/4)) =(8*A/π^2)Σ((-1)^m/(2m+1)^2)*sin((2m+1)ωt+(2m+1)ωT/4) ここで T=2π/ω を代入すると e'(t)=(8*A/π^2)Σ((-1)^m/(2m+1)^2)*sin((2m+1)ωt+(2m+1)ω*(2π/ω)/4) =(8*A/π^2)Σ((-1)^m/(2m+1)^2)*sin((2m+1)ωt+(2m+1)π/2) =(8*A/π^2)*(sin(ωt+π/2)-(1/3^2)*sin(3ωt+3π/2)+(1/5^2)*sin(5ωt+5π/2)+...) =(8*A/π^2)*(cos(ωt)+(1/3^2)*cos(3ωt)+(1/5^2)*cos(5ωt)+...) ということになる。 これらのことから、同じ波形の位相をシフトした場合、スペクトルの絶対値は変わらないが、位相が異なってくることになる。 |
| webadm | 投稿日時: 2009-8-25 21:34 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【26】方形波のFourier級数展開 次ぎは以下のような位相がずれて直流バイアスがかかった方形波のFourier級数展開問題
著者と同じやりかたではつまらないので別のやりかたで解いてみよう。 波形を式で表すと e(t)=(1+a)*A (0≦t≦T/4) =-(1-a)*A (T/4≦t≦3T/4) =(1+a)*A (3T/4≦t≦T) これは偶関数波であるのでFourier級数展開は e(t)=(1/2)b0+Σbn*cos(nωt) (n=1,∞) の形をとるはずである。従って b0=(4/T)∫e(t)dt (0≦t≦T/2) =(4/T)∫(1+a)*Adt (0≦t≦T/4) +(4/T)∫(-(1-a)*A)dt (T/4≦t≦T/2) =(4*(1+a)*A/T)∫dt (0≦t≦T/4) -(4*(1-a)*A/T)∫dt (T/4≦t≦T/2) =(4*(1+a)*A/T)*(T/4)-(4*(1-a)*A/T)*(T/2-T/4) =(1+a)*A-(1-a)*A =2*a*A bn=(4/T)∫e(t)*cos(nωt)dt (0≦t≦T/2) =(4/T)∫(1+a)*A*cos(nωt)dt (0≦t≦T/4) +(4/T)∫(-(1-a)*A)*cos(nωt)dt (T/4≦t≦T/2) =(4*(1+a)*A/T)∫cos(nωt)dt (0≦t≦T/4) -(4*(1-a)*A/T)∫cos(nωt)dt (T/4≦t≦T/2) =(4*(1+a)*A/T)*(sin(nωT/4)/nω -(4*(1-a)*A/T)*(sin(nωT/2)/nω-sin(nωT/4)/nω) ここで T=2π/ω を代入すると =(4*(1+a)*A/(2π/ω))*(sin(nω*(2π/ω)/4)/nω-(4*(1-a)*A/(2π/ω))*(sin(nω*(2π/ω)/2)/nω-sin(nω*(2π/ω)/4)/nω) =(2*(1+a)*A/π)*sin(nπ/2)/n-(2*(1-a)*A/π)*(sin(nπ)/n-sin(nπ/2)/n) =(2*(1+a)*A/π)*sin(nπ/2)/n+(2*(1-a)*A/π)*sin(nπ/2)/n =(4*A/π)*sin(nπ/2)/n =(4*A/π)*sin((2m+1)π/2)/(2m+1) (m=0,∞) =(4*A/π)*(-1)^m/(2m+1) ということになる。すなわち e(t)=(1/2)*(2*a*A)+Σ((4*A/π)*(-1)^m/(2m+1))*cos((2m+1)ωt) =a*A+(4*A/π)*(cos(ωt)-(1/3)*cos(3ωt)+(1/5)*cos(5ωt)-...) ということになる。プロットしてみると wxplot2d([(4*(cos(5*x)/5-cos(3*x)/3+cos(x)))/%pi+0.75], [x,-2*%pi,2*%pi])$ 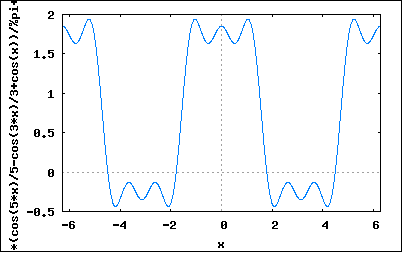 著者は波形が以前の問題に出てきた偶関数かつ対称波の方形波の位相がT/4左にずれてかつ直流バイアスがかかったものとして、以前の問題のFourier級数展開の式を流用して手短に導き出している。 P.S 最初波形を偶数波かつ対称波として解いても同じ結果が得られたが、厳密には直流バイアスがかかった波形は対称波の定義を満たさないので誤りであった。訂正して偶数波としてFourier級数展開すると結果的に対称波の性質である奇数次の項だけになる。これは直流バイアスを取り除けば偶数波で対称波であるのだから、当たり前の話である。直流バイアスを加えても基本波や高調波のスペクトルには影響を与えないことが見てとれる。 基本波と高調波のスペクトルに影響を与えるのは繰り返し波形の形そのもののユニークさであることも定性的に見てとれる。ディーティ比を変えるとスペクトル分布が変わるとか、極性や波形の向きを逆にしてもスペクトルの絶対値そのものは変わらず位相だけが変化しそうだというのもなんとなく予測できる。 |
| webadm | 投稿日時: 2009-8-26 1:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【27】ひずみ波の実効値、電力および力率 次の問題は以下のように電圧と電流の波形が与えられている場合に、それぞれの実効値と電力及び力率を求めよというもの。
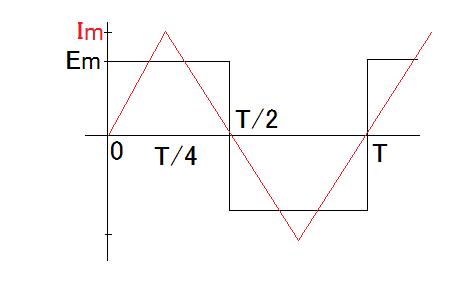 いずれも対称な奇関数波である方形波と三角波であるので、以前の問題やFourier級数展開の公式から e(t)=(4*Em/π)*(sin(ωt)+(1/3)*sin(3ωt)+(1/5)*sin(5ωt)+...) i(t)=(8*Im/π^2)*(sin(ωt)-(1/3^2)*sin(3ωt)+(1/5^2)*sin(5ωt)-...) と表すことができる。 また実効値は対称波であるのとさらに半周期は1/4周期と対称なので |E|=sqrt((4/T)∫e(t)^2dt) (0≦t≦T/4) =sqrt((4/T)∫Em^2dt) =Em*sqrt((4/T)*(T/4) =Em |I|=sqrt((4/T)∫i(t)^2dt) (0≦t≦T/4) =sqrt((4/T)∫(Im*t/(T/4))^2dt) =Im*sqrt((64/T^3)∫t^2dt) =Im|*sqrt((64/T^3)*(T^3/192)) =Im*sqrt(1/3) =Im/√3 ということになる。 有効電力は瞬時値電力の平均値なので Pa=(1/T)∫e(t)*i(t)dt (0≦t≦T) =(4/T)∫e(t)*i(t)dt (0≦t≦T/4) =(4/T)∫Em*(Im*t/(T/4))dt =(16*Em*Im/T^2)∫tdt =(16*Em*Im/T^2)*(T^2/32) =Em*Im/2 ということになる。 最後に力率は有効電力と無効電力の比なので cosφ=Pa/|E||I| =(Em*Im/2)/(Em*Im/√3) =√3/2 ということになる。 著者はFourier級数展開の式から有効電力を導くために、無限級数の極限値の公式を使っている。そうしなくても波形の対称性から1/4周期だけ計算すればそれを4倍すればよい。突然無限級数を持ち出すのは詐欺くさい。 |
| webadm | 投稿日時: 2009-8-26 2:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【28】全波整流波電圧のFourier級数展開と波形率、波高率 次の問題は全波整流波電圧のFourier級数展開を求め、その波形率と波高率を求めよというもの。
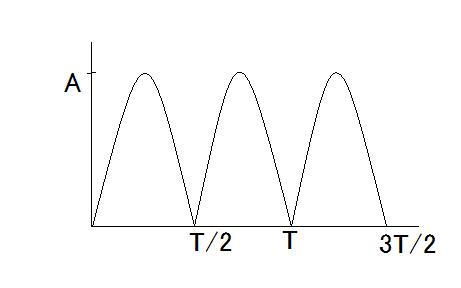 波形を式で表すと e(t)=A*sin(ωt) (0≦t≦T/2) =-A*sin(ωt) (T/2≦t≦T) この波形は遇関数波で、1/4周期毎に対称なのでそのFourier級数展開は e(t)=(1/2)b0+Σbn*cos(nωt) の形をとるはずである。従って b0=(4/T)∫e(t)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)dt =(4*A/T)∫sin(ωt)dt =(4*A/T)*(1/ω-cos(ωT/2)/ω) ここで ω=2π/T を代入すると b0=(4*A/T)*(1/(2π/T)-cos((2π/T)*T/2)/(2π/T)) =(2*A/π)*(1-cos(π)) =4*A/π また bn=(4/T)∫e(t)*cos(nωt)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)*cos(nωt)dt =(4*A/T)∫sin(ωt)*cos(nωt)dt =(4*A/T)*(-((n-1)*cos(((n+1)ωT)/2)+(-n-1)*cos(((n-1)ωT)/2))/((2*n^2-2)ω)-1/((n^2-1)ω) ここで ω=2π/T を代入すると bn=(4*A/T)*(((-cos(nπ)-1)*T)/(2πn^2-2π)) =-(2*A/π)*(cos(nπ)+1)/(n^2-1) =-(2*A/π)*((-1)^n+1)/(n^2-1) (n≠1) =-(4*A/π)/((2m)^2-1) (m=1,∞) ということになる。n=1の場合には別途求める必要がある b1=(4/T)∫e(t)*cos(ωt)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)*cos(ωt)dt =(4*A/T)∫sin(ωt)*cos(ωt)dt =(4*A/T)*(1/2ω-cos(ωT/2)^2/2ω) ここで ω=2π/T を代入すると b1=(4*A/T)*(1/2*(2π/T)-cos((2π/T)*T/2)^2/2*(2π/T)) =(A/π)*(1-cos(π)^2) =(A/π)*(1-(-1)^2) =0 ということになる。従ってFourier級数展開は e(t)=(1/2)*(4*A/π)+Σ(-(4*A/π)/((2m)^2-1))*cos((2m)ωt) (m=1,∞) =(4*A/π)*(1/2-(1/3)*cos(2ωt)-(1/15)*cos(4ωt)-(1/35)*cos(6ωt)-...) ということになる。 なんと整流前の基本波は含まれておらず、偶数次の高調波から成ることがわかる。 波形率は実効値と平均値の比なので 波形率=実効値/平均値 =sqrt((1/T)∫e(t)^2dt)/(1/T)∫e(t)dt (0≦t≦T) =sqrt((4/T)∫e(t)^2dt)/(4/T)∫e(t)dt (0≦t≦T/4) =sqrt((4/T)∫(A*sin(ωt))^2dt/(4/T)∫A*sin(ωt)dt =sqrt((4*A^2/T)∫(1/2-cos(2ωt)/2)dt/(4*A/T)∫sin(ωt)dt =2*A*sqrt((1/T)*(-(2*sin(ωT/2)-ωT)/8ω)/(4*A/T)*(-(cos(ωT/4)-1)/ω) ここで ω=2π/T を代入すると 波形率=2*A*sqrt((1/T)*(-(2*sin((2π/T)*T/2)-(2π/T)*T)/8*(2π/T))/(4*A/T)*(-(cos((2π/T)*T/4)-1)/(2π/T)) =2*A*sqrt(1/8)/(2*A)*(1/π) =π*sqrt(1/8) =π/2√2 ということになる。 また波高率は最大値と実効値の比なので 波高率=最大値/実効値 =A/2*A*sqrt(1/8) =1/2*sqrt(1/8) =1/2*(1/2√2) =√2 ということになる。 |
| webadm | 投稿日時: 2009-8-26 2:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3112 |
【29】全波整流波電圧の負荷電力 次の問題は前問の全波整流波電圧を抵抗に加えた場合に図の電圧計と電流計の指示から負荷電力を求めよというもの
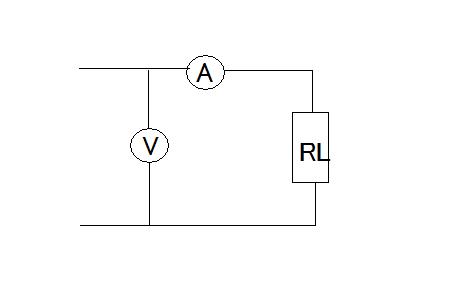 題意では以下の2つの計器について問われている。 (1)熱線型計器の場合 (2)可動コイル型計器の場合 いきなり計器の型が出てきたので困惑してしまう。 調べてみると熱線型とは、後に整流型とかTrue RMS型が現れる以前にあった原始的な交流メーターで、電流をいったん熱(I^2*R)に変換しそれによって熱伝対に発生する電圧から電流の実効値を表示するもの。しかし記憶ではFlukeから熱型と称するディジタルマルチメーターが出ていたと思うのだが、あれは本当に熱型なのだろうか、それともTrue RMSの別名なのだろうか? 一方可動コイル型は本来は直流電流を測るものだが、整流波を加えれば入力信号の平均値を示すことになる。 従って (1)の場合は、電圧および電流とも実効値なので消費電力は Pa=|E|*|I| =sqrt((1/T)∫e(t)^2dt)*sqrt((1/T)∫i(t)^2dt) (0≦t≦T) =sqrt((4/T)∫e(t)^2dt)*sqrt((4/T)∫i(t)^2dt) (0≦t≦T/4) =sqrt((4/T)∫(Em*sin(ωt))^2dt)*sqrt((4/T)∫(Im*sin(ωt))^2dt) =4*Em*Im*sqrt((1/T)∫sin(ωt)^2dt)*sqrt((1/T)∫sin(ωt)^2dt) =4*Em*Im*sqrt((1/T)∫(1/2-cos(2ωt)/2)dt)*sqrt((1/T)∫(1/2-cos(2ωt)/2)dt) =4*Em*Im*sqrt(1/8)*sqrt(1/8) =Em*Im/2 ということになる。 一方(2)の場合指示値は平均値なので電圧と電流の平均値は E=(1/T)∫e(t)dt (0≦t≦T) =(4/T)∫e(t)dt (0≦t≦T/4) =(4/T)∫Em*sin(ωt)dt =(4*Em/T)∫sin(ωt)dt =(4*Em/T)*(1/ω-cos(ωT/4)/ω) ここで ω=2π/T を代入すると E=(4*Em/T)*(1/(2π/T)-cos((2π/T)*T/4)/(2π/T)) =(2*Em/π)*(1-cos(π/2)) =2*Em/π I=(1/T)∫i(t)dt (0≦t≦T) =(4/T)∫i(t)dt (0≦t≦T/4) =(4/T)∫Im*sin(ωt)dt =(4*Im/T)∫sin(ωt)dt =(4*Im/T)*(1/ω-cos(ωT/4)/ω) ここで ω=2π/T を代入すると E=(4*Im/T)*(1/(2π/T)-cos((2π/T)*T/4)/(2π/T)) =(2*Im/π)*(1-cos(π/2)) =2*Im/π 平均値を使って電圧と電流の最大値を表すと Em=Eπ/2 Im=Iπ/2 従って消費電力は Pa=Em*Im/2 =(Eπ/2)*(Iπ/2)/2 =E*I*π^2/8 として導くことができる。 |
| « 1 2 (3) 4 5 6 ... 8 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

