| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-10-1 20:49 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【70】三角パルスのFourier変換 次ぎの問題は以下の様な三角パルスのFourier変換を求めよというもの。
著者とは違った方法で解いてみよう。 この波形は以下の式で表すことができる y(t)=(1/T)(f*f)(t) =(1/T)∫f(t')f(t-t')dt' f(t)=1 (-T/2≦t≦T/2) =0 (-T/2>t>T/2) すなわち幅がTで高さが1の方形パルス同志の合成積に1/Tを乗じたものである。以下の図のように同じ方形パルスが-∞の方から移動してきて+∞に去っていく中でもう一つの同じ形の方形パルスと重なった部分の面積が合成積である。 これのFourier変換は合成積のFourier変換対の公式を用いて導くことができる、すなわち (f*g)(t) <=> F(ω)G(ω) 従ってこの場合 (f*f)(t) <=> F(ω)F(ω) ということになるのでf(t)のFourier変換は以前の問題の解より F(ω)=2*sin(ωT/2)/ω であるので求めるFourier変換は ∫(1/T)(f*f)(t)*exp(-jωt)dt =(1/T)F(ω)F(ω) =(1/T)(2*sin(ωT/2)/ω)^2 =(1/T)4*sin(ωT/2)^2/ω^2 =4*sin(ωT/2)^2/Tω^2 ということになる。 T=1としてプロットしてみると wxplot2d([(4*sin(x/2)^2)/x^2], [x,-10*%pi,10*%pi])$ 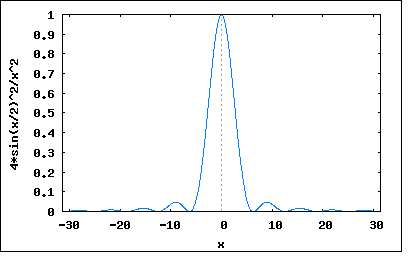 という形になる。 |
| webadm | 投稿日時: 2009-10-1 22:01 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【71】三角パルスによるデルタ関数の近似 次ぎの問題は前問の応用で、三角パルスによってデルタ関数のFourier変換がF(ω)=1になることを導けというもの。
前問の三角パルスの合成積のFourier変換式 F(ω)=4*sin(ωT/2)^2/Tω^2 これは以下のように書き直すことができる F(ω)=4*sin(ωT/2)^2/Tω^2 =T*sin(ωT/2)^2/(ωT/2)^2 これに1/Tを乗じると F'(ω)=(1/T)F(ω) =sin(ωT/2)^2/(ωT/2)^2 =(sin(ωT/2)/(ωT/2))^2 =sinc(ωT/2)^2 従ってT→0とした場合の極限値を求めると lim F'(ω) (T→0) =lim sinc(ωT/2)^2 (T→0) =(lim sinc(ωT/2))^2 =(lim sin(ωT/2)/(ωT/2))^2 =(lim (sin(ωT/2))'/(ωT/2)')^2 =(lim (ω*cos(ωT/2)/2)/(ω/2))^2 =((ω*cos(0)/2)/(ω/2))^2 =((ω/2)/(ω/2))^2 =(1)^2 =1 従って lim F'(ω) (T→0) =1 ということになりデルタ関数のFourier変換となることが確認できた。 これはT→0にするとスペクトルの裾野が無限大に広がって直線になるということを意味する。同時に元の三角パルスはt=0で+∞を取りそれ以外では0に収束するデルタ関数を近似する。 デルタ関数を近似する関数はいくつもあり、面積が1になるような高さが1/Tで幅がTの方形パルスもT→0にするとデルタ関数を近似する。当然ながらそれらの合成積もデルタ関数であるということもわかる。 |
| webadm | 投稿日時: 2009-10-2 9:50 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【72】指数関数のFourier変換 次ぎは指数関数のFourier変換。
これまで直流、正弦波、余弦波、方形パルス、三角パルスなど比較的基本的な波形のFourier変換を求めてきたけれども指数関数もそのひとつ。実は基本関数が一番Fourier変換が求め難いという理由から、Fourier変換対を示すだけですませている本も多い。 負の乗数を伴う指数関数は数学的には優等生で、すべての区間において無限回に微分可能。 しかし積分に関しても優等性かというとそうでもなく、 y(t)=exp(-at) ただし a>0 t≧0の範囲ではy(t)は有界であるがt<0の範囲ではそうではない。Fourier変換は関数の値が有限個の特異点を除いては有界でないと収束しないというディレクレの条件からすると上の関数の場合負のtの範囲に関してはFourier変換が成り立たない。 従って題意では y(t)=exp(-at) (t≧0) =0 (t<0) ただし a > 0 ということになっている。 これならFourier変換が可能なのでやってみることにする F(ω)=∫y(t)*exp(-jωt)dt (t=-∞,+∞) =∫exp(-at)*exp(-jωt)dt (t=0,+∞) =∫exp(-(a+jω)t)dt =-exp(-(a+jω)∞)/(a+jω)+exp(-(a+jω)0)/(a+jω) =exp(0)/(a+jω) =1/(a+jω) ということになる。 スペクトルと位相をプロットするために指数表記に直すと F(ω)=1/(a+jω) =(1/sqrt(a^2+ω^2))*exp(-j*atan(ω/a)) a=1とおいてプロットすると wxplot2d([1/sqrt(1+x^2),-atan(x)], [x,-5,5])$ 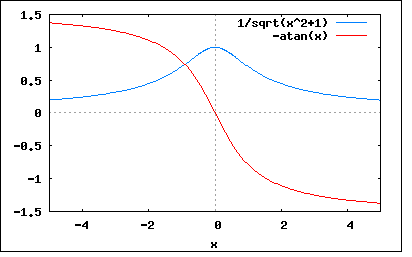 ということになる。 |
| webadm | 投稿日時: 2009-10-2 10:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【73】RC直列回路の伝達関数 しばらくの間Fourier変換に関する公式を解くような問題ばかりでうんざりした人もいるかもしれない。これから先の残りの問題はようやく工学問題に関するもの。
最初のものはRC直列回路の周波数領域での伝達関数を求めよといういきなり習ってもいない伝達関数が出てきた。 伝達関数は制御理論の中心的な概念だけれども長らくの間電気理論とは別の工学理論として発展してきた経緯がある。しかし真空管やトランジスタなどの能動素子を使った電子回路の時代に入ってやおら電気電子と制御理論の間に橋がかかって相互に理論がつながるようになったのはつい近代のことである。また電子回路による制御は連続時間系(いわゆるアナログ)であることは、それ以前の機構式や力学的な制御システムと変わりなかった。それが変わったのはデジタルコンピューターが登場してA/D変換器による連続時間信号を離散時間信号に変換して処理するデジタル信号理論が発展してからである。以降それに基づくデジタル制御やデジタル信号処理があっという間に今日全盛を極めるに至っている。 本書の著者がFourier変換にかなりページ数を多く割いているのも、こうした時代的な背景と著者の読者に対する思い入れがあるのは明らかである。およそ初学者にとっては、電気回路の古典的な理論を学ぶのだけでも大変なのに、教える側としては、それだけでは社会にでてはなはだ不十分であるということを察しているわけだ。 そういう意味ではデジタルコンピュータ登場以前に形作れ、延々と未だにのさばっている古い文部省の学習指導要領体系がすでに「終わっている」と言える。本来ならば早急に制御工学と電気電子回路理論を融合して知識体系として再構成するなどの努力が必要であろう。 話をもとにもどそう。 題意は以下のようなRC直列回路の周波数領域伝達関数を求めよというもの。 あらかじめ題意では上記回路のインパルス応答が以下のように与えられている h(t)=(1/RC)*exp(-t/RC) (t>0) =0 (t<0) インパルス応答とは制御理論で入力信号としてデルタ関数を与えた場合の出力として現れる応答波形のことである。デルタ関数はFourier変換するとすべての周波数が一様に含まれているので、それを入力に与えた場合の出力信号をFourier変換すれば周波数領域の応答(伝達関数)を知ることができるというわけである。 従って、周波数領域での伝達関数を知るには、デルタ関数を入力として与えた場合の出力応答波形をFourier変換すればよいことになる。 従ってそのFourier変換は H(ω)=∫h(t)*exp(-jωt)dt (t=-∞,+∞) =∫(1/RC)*exp(-t/RC)*exp(-jωt)dt (t=0,+∞) =(1/RC)∫exp(-(1/RC+jω)t)dt =(1/RC)(-exp(-(1/RC+jω)∞)/(1/RC+jω)+exp(-(1/RC+jω)0)/(1/RC+jω)) =(1/RC)*exp(0)/(1/RC+jω) =1/(1+jωRC) ということになる。 これは入力周波数が高くなるにつれ出力低下していくローパスフィルターの特性そのものである。 RC=1として周波数と位相特性をプロットしてみると wxplot2d([sqrt(1/(x^2+1)),-atan(x)], [x,-5,5])$ 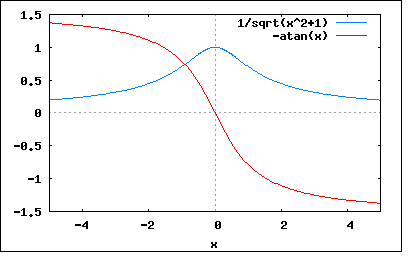 ということになる。こうした周波数と位相特性をプロットしたグラフを制御工学ではボーデ線図と呼ぶ。 伝達関数は出力関数を分子に入力関数を分母とする有理関数である。 その意義は、伝達関数に任意の入力関数式を乗じればそれに対する出力波形に対応する式になり、逆変換すれば時間領域の関数式が得られるという点で制御システムや電子回路の特性を予測するのに欠くことができない概念である。 電子回路や制御回路の設計ではもっぱら意図したような入力に対して意図した出力が得られるように伝達関数を設計もしくは解析できることが不可欠となる。数学的に設計は逆問題、解析は順問題である。学校や参考書では順問題のみを扱い、逆問題は読者の課題ということになる。 本格的な回路の周波数領域の伝達関数を解析するには後に学ぶことになるラプラス変換が使用される。かつてはヘビサイドの演算子法が担っていたが戦後ラプラス変換にすり替わってしまった。ヘビサイドが演算子法を考案した当時はまだ量子物理学は登場しておらずデルタ関数すらなかったが、その積分関数である単位ステップ関数を使って回路の過渡応答を解析する方法を確立した。現在もアナログ回路の時間領域での応答特性を観測するためにステップ入力を与える方法が依然として使われている。これはインパルス信号が理想的だが数学的に机上でしか扱うことができず実回路では実現し得ないことが理由である。机上での解析ではデルタ関数を使って解析が行われる。デルタ関数の変わりに周波数領域の応答特性を測定するための信号源としてスイープジェネレータがある。ただしこれは時間で周波数を変化させるので周波数領域の応答を調べるのには有用だが時間領域での応答を調べることはできない。 |
| webadm | 投稿日時: 2009-10-3 6:49 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【74】理想低域フィルタのインパルス応答 次ぎは理想低域フィルタのインパルス応答を求めよというもの。
理想低域フィルタというのは以下の様に周波数領域でカットオフ周波数より低い周波数のみを通過させそのはそれ以外は遮断するというもの。 題意では周波数領域の伝達関数が以下のように与えられている H(f)=exp(-j2πf*t0) |f|<B/2 =0 |f|>B/2 周波数領域の伝達関数は入力にインパルス信号を与えた際に出力されるインパルス応答波形をFourier変換したものであるというのを思い出せば、それを逆Fourier変換すれば元のインパルス応答波形を得ることができるはずである。 普通に逆Fourier変換をすればいいのだが、著者の解と違った方法でやってみよう。 H(f)の式を各周波数の式に書き直すと H(ω)=exp(-jω*t0) |ω|<W/2 =0 |ω|>W/2 ここで W=2πB/2 =πB ここでH(ω)は以下の2つのFourier変換の合成として表すことができる H(ω)=F(ω)*exp(-jω*t0) F(ω)=1 |ω|<W/2 =0 |ω|>W/2 と書き換えることができる。 これはF(ω)の逆Fourier変換であるf(t)を時間軸上で右方向にt0だけ推移させたもののFourier変換の形である。 F(ω)の逆Fourier変換は f(t)=(1/2π)∫F(ω)*exp(jωt)dω =(1/2π)(∫exp(jωt)dω (ω=0,W) +∫exp(jωt)dω) (ω=-W,0) =(1/2π)((1/jt)exp(jWt)-(1/jt)exp(0) +(1/jt)exp(0)-(1/jt)exp(-jWt)) =(1/2π)((1/jt)exp(jWt)-(1/jt)exp(-jWt)) =sin(Wt)/πt =sin(πBt)/πt =B*sin(πBt)/πBt =B*sinc(πBt) ということになる。 従って求めるインパルス応答は h(t)=B*sinc(πB(t-t0)) =B*sin(πB(t-t0))/πB(t-t0) ということになる。 B=1, t0=1と置いてプロットしてみると wxplot2d([sin(%pi*(t-1))/(%pi*(t-1))], [t,-5,5])$ 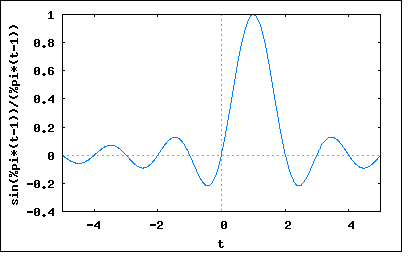 t=t0以前の無限に過去から既に出力が変化していることが見てとれる。入力信号はt=t0でインパルス信号が入るので、それ以前には入力信号は0のはずなので出力が変化するのは矛盾する。これは理想低域フィルタが因果律を満足しないため現実の回路では実現できないと言われる所以である。 ある入力事象が発生する以前には予めその予兆が異次元であるとすればそれが出力に出てくると考えられないこともない。しかしそれはローマカトリックが教えるようにマリアが天使が現れてキリストの受胎を告知した夢を見たという逸話のようなものである。そう考えれと、ある重大な意味を持つ事象は予め計画されていたという意味を持ち、誰がそれを計画したのかという疑問を生み、最終的には三位一体の理論に帰着することになる。自然哲学的には、宇宙はいつ現れたのか?突然現れたとしたら予めそうなる理由があってしかるべきではないかという考えが出てくるのは当然である。この問題は今日なお答えが得られていない。数学や工学理論が今日無味乾燥なものになったのは自然哲学が排除されてしまったためではないかと思われる。今こそ自然哲学と数学や工学を融合して再構成する時かもしれない。そうすれば学ぶのが面白くなる。 著者も珍しく解説に熱を入れているように問題では振幅特性と位相特性を勝手に定義して与えているが、実際の回路やシステムではその2つには依存関係があり、一方を変えると他方も影響を受けて変わってしまうので好きに決めることができないのである。たとえば一定の周波数範囲だけ位相も振幅も変えずに通過させる理想的なバンドパスフィルターなどというのは実現できない。しかし数式上では自由に与えることができるので後の問題で出てくる有名なナイキスト-シャノンのサンプリング定理はそうした理想低域フィルターを利用している。シャノンは連続時間系信号をナイキスト周波数でサンプルした離散時間信号列を理想低域フィルターを通すことによって元の連続時間系信号を復元することができることを数学的に証明した。日本人の染谷氏も同じ頃にまったく独自に同じ理論を本に書いたが大戦中のために知られることはなかった。 |
| webadm | 投稿日時: 2009-10-4 1:11 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【75】理想低域フィルタのステップ応答 次ぎの問題は前問のフィルタに単位ステップ入力を与えた場合の時間領域応答を求めよというもの。
これも著者の解とは違った方法で解いてみよう。 既に前問で理想低域フィルタの周波数領域伝達関数が与えられているので、単位ステップ関数のFourier変換とその伝達関数の積が出力のFourier変換になるので、それを逆Fourier変換すれば時間領域でのステップ応答が得られるはず。 単位ステップ関数のFourier変換は以前の問題ですでにやった通り F(ω)=πδ(ω)+1/jω また理想低域フィルタの伝達関数は H(ω)=exp(-jω*t0) |ω|<πB =0 |ω|>πB 従ってステップ入力に対する時間軸応答は y(t)=(1/2π)∫H(ω)F(ω)*exp(jωt)dω (ω=-∞,+∞) =(1/2π)∫exp(-jω*t0)*(πδ(ω)+1/jω)*exp(jωt)dω (ω=-πB,+πB) =(1/2π)∫(πδ(ω)+1/jω)*exp(jω(t-t0))dω =(1/2π)(∫πδ(ω)*exp(jω(t-t0))dω+∫(1/jω)*exp(jω(t-t0))dω) =(1/2π)(π*exp(0)+∫(1/jω)*exp(jω(t-t0))dω) =1/2+(1/2π)∫(1/jω)*exp(jω(t-t0))dω こっからどうすんだこれ? 第二項目の積分式を変形すると y(t)=1/2+(1/2π)∫(1/jω)*exp(jω(t-t0))dω (ω=-πB,πB) =1/2+(1/2π)∫(1/jω)*exp(jω(t-t0))dω (ω=-πB,0) +(1/2π)∫(1/jω)*exp(jω(t-t0))dω (ω=0,πB) =1/2+(1/2π)∫(1/-jω)*exp(-jω(t-t0))dω (ω=0,πB) +(1/2π)∫(1/jω)*exp(jω(t-t0))dω (ω=0,πB) =1/2+(1/2π)∫(1/jω)(exp(jω(t-t0))-exp(-jω(t-t0)))dω (ω=0,πB) =1/2+(1/2π)∫(2*sin(ω(t-t0))/ω)dω (ω=0,πB) =1/2+(1/π)∫(sin(ω(t-t0))/ω)dω (ω=0,πB) ここで ω=x/(t-t0) と積分変数変換すると dω/dx=1/(t-t0) ∴dω=(1/(t-t0))dx これを代入すると y(t)=1/2+(1/π)∫(sin(x)/x)dx (x=0,πB(t-t0)) ということになる。ふう、やっと形になった。 しかしこれどうやってプロットするんだ、このままの式でMaximaに食わせたら永遠と応答が返ってこないんだが(;´Д`) 積分式を展開していっても永遠に最後の積分項が無くならないし(;´Д`) どうやらこれは正弦積分関数といって初等関数で表すことのできない特殊関数になるらしい。 いろいろな本には波形が描いてあるが、どうやってプロットしたのだろう。昔の人は手で計算したのか? この数値計算方法だけで論文が書けるらしい。 ようやくみつけた級数の近似式でB=1,t0=1としてプロットしてみた wxplot2d([1/2+(1/%pi)*sum(((-1)^(k))*((%pi*(t-1))^(2*k+1))/((2*k+1)*(2*k+1)!), k, 0, 100), simpsum], [t,-5,5])$ 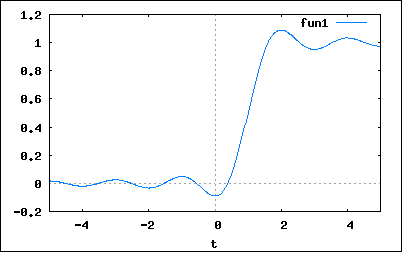 入力はt=0から立ち上がる単位ステップ関数だが、t=0で既に出力が出ていてそれ以前からも変化しているのは因果律に反する。これだけ労力(かなり高次項まで計算しないと|t|が大きくなるにつれ誤差が急拡大する)をかけてプロットしても現実にはあり得ない波形ということになる。不連続点(t0=1)前後にはGibbs現象によるアンダーシュートとオーバーシュートが見られる。それでも畳み込み積分、伝達関数、フィルタリングなどの共通概念を理解するのに役立つ。 このため連続時間系システムの過渡応答解析に用いられるのはもっぱらFourier変換ではなくラプラス変換になっている。ラプラス変換はt<0を扱わないため因果律を満たすためである。後にラプラス変換で同じようなことを勉強するはめになる。 |
| webadm | 投稿日時: 2009-10-4 21:30 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【76】既知のインパルス応答から方形パルス応答を求める 次ぎの問題は以下のように予め時間軸領域でのインパルス応答関数がわかっている回路に方形パルスを入力した場合に出力がどうなるか求めよというもの。
既知のインパルス時間軸応答関数は h(t)=h0*exp(-t/T) (t>0) =0 (t<0) 与える方形パルス関数は x(t)=A (|t|<T/2) =0 (|t|>T/2) これも著者の解とは違うやりかたで解いてみよう。 ストラテジーとしては予めわかっているインパルス時間軸応答関数をFourier変換し周波数伝達関数H(ω)を得る。次ぎに与えられた方形パルス関数を同様にFourier変換し入力周波数スペクトル関数X(ω)を得る。周波数伝達関数と入力周波数スペクトル関数の積H(ω)X(ω)を逆Fourier変換すれば方形パルス入力に対する時間軸応答関数y(t)が得られるはずである。 最初に周波数伝達関数を求めてみよう H(ω)=∫h(t)*exp(-jωt)dt (t=-∞,+∞) =∫h0*exp(-t/T)*exp(-jωt)dt (t=0,+∞) =h0∫exp(-(1/T+jω)t)dt =h0*(-exp(-(1/T+jω)∞)/(1/T+jω)+exp(-(1/T+jω)0)/(1/T+jω)) =h0/(1/T+jω) ということになる。 次ぎに方形パルス入力をFourier変換すると X(ω)=∫x(t)*exp(-jωt)dt (t=-∞,+∞) =∫A*exp(-jωt)dt (t=-T/2,T/2) =-A*exp(-jωT/2)/jω+A*exp(jωT/2)/jω =(A/jω)(exp(jωT/2)-exp(-jωT/2)) ということになる。これはちょうどsgn(t+T/2)-sgn(t-T/2)のFourier変換を意味する。図で表すと sgn(t+T/2)-sgn(t-T/2)が実は方計パルスの式であったことをFourier変換した結果から気づいたわけだ。 従って求める方形パルス応答関数は y(t)=(1/2π)∫(h0/(1/T+jω))((A/jω)(exp(jωT/2)-exp(-jωT/2)))*exp(jωt)dω =(1/2π)∫(A*h0/jω(1/T+jω))(exp(jωT/2)*exp(jωt))dω-(1/2π)∫(A*h0/jω(1/T+jω))(exp(-jωT/2)*exp(jωt))dω =(1/2π)∫(A*h0/jω(1/T+jω))*exp(jωT/2)*exp(jωt)dω-(1/2π)∫(A*h0/jω(1/T+jω))*exp(-jωT/2)*exp(jωt)dω これは周波数スペクトルが(A*h0/jω(1/T+jω))である応答関数を時間軸上で左にT/2と右にT/2それぞれ推移させて後者を符号反転し合成したものであることを意味する。 一方(A*h0/jω(1/T+jω)は(A/2)*sgn(t)関数のFourier変換である(A/jω)とh0*exp(-t/T)のFoureir変換である(h0/(1/T+jω)の積である。従ってその逆Fourier変換は(A/2)*sgn(t)とh0*exp(-t/T)の畳み込み積分であることを意味する。 y(t)=∫(A/2)*sgn(t+T/2)*h0*exp(-(t-t'+T/2)/T)dt'-∫(A/2)*sgn(t-T/2)*h0*exp(-(t-t'-T/2)/T)dt' (t'=-∞,+∞) =(A*h0/2)(∫sgn(t+T/2)*exp(-(t-t')/T-1/2)dt'-∫sng(t-T/2)*exp(-(t-t')/T+1/2)dt') さてここからどうするか sgn(t)=1 (t>0) =0 (t=0) =-1 (t<0) なので sgn(t+T/2)=1 (t>-T/2) =0 (t=-T/2) =-1 (t<-T/2) sgn(t-T/2)=1 (t>T/2) =0 (t=T/2) =-1 (t<T/2) したがって以下の3つの区間 (1) t > T/2 sgn(t+T/2)=1 sgn(t-T/2)=1 (2) -T/2<t<T/2 sgn(t+T/2)=1 sgn(t-T/2)=-1 (3) t < -T/2 sgn(t+T/2)=-1 sgn(t-T/2)=-1 についてそれぞれ考える必要がある。 むう、わかんね〜(´Д`;) 挫折しそ、逆Fourier変換の式から素直にやり直そうかな... y(t)=(1/2π)∫(h0/(1/T+jω))((A/jω)(exp(jωT/2)-exp(-jωT/2)))*exp(jωt)dω 諸悪の根元は (h0/(1/T+jω))(A/jω) という分数の積である。これが畳み込み積分に逆Fourier変換されるのはわかるが、そのアプローチは茨の道だった。 これが部分分数の和に展開できれば楽なのだが そこでまだ習っていないヘビサイドの展開定理にご登場願おう ヘビサイドの展開定理は彼が独自の演算子法を使って微分方程式を変換した結果として出てくる多項式を伴う分数を部分分数に展開し逆変換を容易にするために発見した定理である。 一般的な定理の紹介は他所に譲るとして、ここでは上記の式の展開に焦点をあててやってみよう 最初に以下のような展開が成り立つとする (h0/(1/T+jω))(A/jω)=k1/(1/T+jω)+k2/jω 未知数k1,k2を求めれば良いので両辺に(1/T+jω)(A/jω)を乗じると A*h0=k1*jω+k2*(1/T+jω) ということになる。ここで右辺の第二項を消去するためにjω=-1/Tを代入すると A*h0=k1*(-1/T) ∴k1=-A*h0*T 同様に第一項を消去するためにjω=0を代入すると A*h0=k2*(1/T) ∴k2=A*h0*T ということになる。従って問題の分数式は (h0/(1/T+jω))(A/jω)=k1/(1/T+jω)+k2/jω =(-A*h0*T)/(1/T+jω)+(A*h0*T)/jω =(A*h0*T)*(1/jω-1/(1/T+jω)) ということになる。これでもはや分数の積ではなくなるので逆Fourier変換結果に畳み込み積分は現れなくなる。 そこで既に知っているFourier変換対の公式により 1/jω <=> (1/2)sgn(t) 1/(1/T+jω) <=> exp(-t/T) F(ω)*exp(-jω*t0) <=> f(t-t0) という関係が成り立つ。 従って応答の式は y(t)=(1/2π)∫(h0/(1/T+jω))((A/jω)(exp(jωT/2)-exp(-jωT/2)))*exp(jωt)dω =(1/2π)∫(A*h0*T)*(1/jω-1/(1/T+jω))*(exp(jωT/2)-exp(-jωT/2))*exp(jωt)dω =(1/2π)∫(A*h0*T)*(1/jω)*(exp(jωT/2)-exp(-jωT/2))dω-(1/2π)∫(A*h0*T)*(1/(1/T+jω))*(exp(jωT/2)-exp(-jωT/2))dω =(A*h0*T)*(sgn(t+T/2)/2-sgn(t-T/2)/2)-(A*h0/T)*(exp(-(t+T/2)/T)-exp(-(t-T/2)/T)) =(A*h0*T)*(sgn(t+T/2)/2-sgn(t-T/2)/2-exp(-(t+T/2)/T)+exp(-(t-T/2)/T)) =(A*h0*T)*((1/2)*(sgn(t+T/2)-sgn(t-T/2))+exp(-(t-T/2)/T)-exp(-(t+T/2)/T)) ここで再びsgn関数部分は sgn(t+T/2)=1 (t>-T/2) =-1 (t<-T/2) sgn(t-T/2)=1 (t>T/2) =-1 (t<T/2) なので (1/2)(sgn(t+T/2)-sgn(t-T/2))=0 (t>T/2) =1 (-T/2>t>T/2) =0 (t<-T/2) ということになる。 同様に指数関数部分は exp(-(t-T/2)/T)-exp(-(t+T/2)/T)) =exp(-t/T)*(exp(1/2)-exp(-1/2)) (t>T/2) =-exp(-(t+T/2)/T) (-T/2<t<T/2) =0 (t<-T/2) 従って y(t)=(A*h0*T)*((1/2)*(sgn(t+T/2)-sgn(t-T/2))+exp(-(t-T/2)/T)-exp(-(t+T/2)/T)) =(A*h0*T)*exp(-t/T)*(exp(1/2)-exp(-1/2)) (t>T/2) =(A*h0*T)*(1-exp(-(t+T/2)/T)) (-T/2<t<T/2) =0 (t<-T/2) ということになる。 なんだ簡単じゃないか(´∀` ) A=1, h0=1, T=1 としてプロットしてみると wxplot2d([if t>1/2 then (sqrt(%e)-1/sqrt(%e))*%e^(-t) elseif t>-1/2 then 1-%e^(-t -1/2) elseif t<-1/2 then 0 ], [t,-5,5])$ 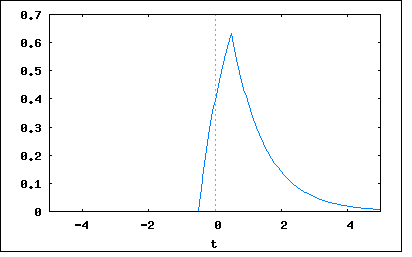 方形パルスが加わるt=-T/2=-0.5までは0でそこから指数関数的に1に近づいていき方形パルスが取り去られるt=T/2=0.5で1-exp(-1)に達しそこから指数関数的に減衰していくというもの。 ところで著者の解を見てみると、いきなり畳み込み積分の式を導出した際に伴う畳み込み積分区間の取り方の根拠がわからないが結果は正しい。 最初にやった逆Fourier変換の式から畳み込み積分を導出する方法が挫折したアプローチを最後まで完遂させるのは読者の課題として残しておこう(´∀` ) |
| webadm | 投稿日時: 2009-10-6 15:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
【77】ナイキスト−シャノンのサンプリング定理 さていよいよ上巻最後の問題にたどり着いた。ふう、長かった。二年ぐらいかかったろうか、途中2回半年ほどアルバイトに精を出すために休んだから続けてやれば1年ぐらいで終わったかもしれない。休むことは知識を熟成するための肥やしにもなったけどね。
小学生の時に自宅でアサガオとかを栽培したことがあって、最初は種を撒いても一日じゃなにも変わらないのに気づいてかなりモチベーションが下がったけど、毎日継続して水をやったり気にかけたりしていると夏の初めにはつぼみが出来て、いつ咲くのかいつ咲くのかと毎日辛抱していたらある朝知らない間に紫色の大輪の花が咲いていて感動した。その後花は萎れたけど、今度は種が出来て、来年また植えて咲かせる楽しみが出来た。そう一日じゃちょっとじゃ結果が出ないことを知った。感動させる大仕事をなし遂げるにはもっと長い期間、もしくは一生涯じゃすまないぐらいの年月がかかるってこともあるって理解できるようになった。それから辛抱強くなったと思う。 それから遠くの学校に寮住み込みで勉強しにいった時、昔姉が庭に植えたスイセンがそのまま土の中に球根のまま放置されているのを発見して、株分けして植え直してあげたところ、春先に芽が出てきてつぼみを付けるまでに育った。けれども一向に咲く気配が見えない。いつ咲くのだろう、春休みが終わったらまた学校の寮に戻らないといけないので花を見ることはできないかも。とがっかりしていたところ、出かける朝にスイセンの花が全部咲いていると母が教えてくれた、まるでこの日の朝家を離れるのを知っていて送迎してくれているように見えた。花はちっともさぼったりしていない。ひとときも休まず準備する努力をするから美しい花を咲かせることができる。人もそうじゃないかな。 話をもとに戻そう。 問題文は 「帯域制限された連続波形y(t)を離散的な値の集合で表現できることを示せ。」 という簡単な一文であるが、これが本書の著者が用意した本章というか本書の最後の問題である。これはどちらかというと電気回路理論の範疇ではなく、ディジタル信号処理理論の範疇なのだが、もはやそういう古い枠組みは古い時代に勝手に線引きされたものなので、もともとは自然科学に境界線など存在しないのだ。そういう意味で本書の著者が読者に求めているものは遙かに高い。いろいろな時代に色々な国や場所で発展した数学や工学、科学、物理学、化学、生物学、地学などありとあらゆるものは皆どっかでつながるのである。 話をまた元に戻そう。 非常に短い問題文だけど、既にディジタル信号処理理論を少しでも囓った人ならその意味することは一目瞭然なのだが、電気回路を1年囓っただけで、著者が意図している解答を出すのは難しいかもしれない。それでも著者はこの問題を読者に問いたいのだ。そして先へ進んでいって欲しいのだ。 題意に答えるには以下を証明する必要がある ・帯域制限された時間軸領域の連続信号がその周波数スペクトルを保存する形で離散的な数列にサンプリングできること ・上記サンプリング数列から元の帯域制限された連続信号が復元できること この2つはナイキストによって予想され、後にシャノンが数学的に証明したナイキスト−シャノンのサンプリング定理そのものである。 さてこれからその証明を追体験することにする。 まず最初に問題文の中に出てくる用語の意味を知っておかなければならない。 「帯域制限された連続波形」とは何か? Fourier変換を学んだ今なら帯域という意味は周波数領域でスペクトルが占有する幅を意味するといえばわかるかもしれない。しかしFourierがFourier級数を発見してからしばらくはその収束条件や積分可条件、極限値などの手付かずだった解析学の問題に飛び火してしばらくそれらの問題が解決するまでは混沌とした歴史が続いた。それらの混濁の時代が終わり宇宙の晴れ上がりのような時代になってようやくFourier級数やFourier変換を安心して使えるようになった。それからようやくFourier変換の応用が急拡大したわけである。 そのとき時代はすでにアナログ変調による無線通信などの技術が開発されてそれまで多重化できなかった電話回線の通信路がちょうどケーブルTVのように一本の同軸ケーブルで複数の会話を通すことが可能になっていた。そこで問題になったのは、一本の回線になるべくたくさんの会話を歪みなく通すにはどうすればよいか?という点である。 AMラジオ放送は互いの占有帯域が重ならないようにラジオ局に対して周波数割り当てが行われている。ちょっとでも隣接すると少なからず混信をうけるからだ。経験上そういうことが確認されるが、その理由は2つの隣接する変調された信号をFourier変換をしてみるとよくわかる。 2つの隣接する基本搬送周波数の変調信号をFourier変換するとそれぞれの信号AM変調は中心にその基本搬送波の線スペクトルその両脇に側帯波とよばれる変調信号のスペクトルが占有している。従って両基本搬送波が近すぎると、互いの側帯波のスペクトルが重なりあってしまい混信が生じ再生された信号は歪むということがわかる。 これらの検討を直流電信,SSB(single side band),DSB(double side band)の変調方式についてそれぞれ検討した結果をまとめたのがナイキストで、その際にSSBはDSBに比べ半分の占有帯域で済むということを示した。それ以来初期の無線通信を使った電話伝送や衛星通信ではSSBが採用され、アマチュア無線でも占有帯域がDSBの半分で済むSSBが主流になった。同時に一本の伝送路で複数の音声信号を通すにはひとつのDSBが占有する2倍の幅の間隔をおいて帯域を割り当てればよいということも示した。これがナイキストレートと呼ばれるものである。当然ながらナイキストの時代にはまだデジタル技術はなかったし通信も直流電信(テレグラフ)が主流であった。しかしこれがデジタル化時代にも通用する重要なヒントになった。直流電信は矩形波のFourier変換からわかるように無限に広いスペクトル領域を占有するので多重化が望めないのは明らかだった。 シャノンの時代になって彼が属していたベル研究所は新しいデジタル技術であるPCM(パルス符号変調)方式の多重化通話伝送が研究されはじめていた。それまでのアナログ時代ではフィルターで帯域をカットしなければならないほど連続時間信号には数学的に無限の情報が含まれているという認識だった。しかしPCMのように一定間隔でアナログ値をデジタル符号に変換すると情報量はその符号のビット数だけになってしまう。シャノンはこのことからひとつの通信路の情報容量をはじめてbit/秒という単位を導入した。これが情報チャネル理論の草分けである理由である。シャノンの論文の目的はノイズが伴う実際の通信路で誤り無く情報を伝送可能なチャネルの情報容量を見出すというものだった。その過程で、ひとつの信号に関する情報量をどれだけはしょれるかという問いに対してサンプリング定理をそれ以前に発表されている第三者の業績を整理して完結な式と理論にまとめたのである。このことからサンプリング定理はシャノン一人の業績に帰着するものではなく、シャノンが引用したナイキストやWhittakerや、その当時しられていないが同様の理論を発表していた人に帰着すべきというのももっともである。従ってそうした考えから、単にサンプリング定理と呼ばれる傾向にある。 シャノンの貢献はナイキストのアナログの時代では情報量という概念すらなかった、ナイキスト自身はそれを信号に含まれる"inteligence"という曖昧な表現をしている。それらはFourier変換して周波数領域で見ると占有幅の広さとして現れてくる程度の認識しかできなかったのはデジタル時代以前であるからしかたあるまい。 これらのことから「帯域制限された」という意味は以下のように解釈することができる 連続時間領域の信号f(t)をFourier変換したスペクトルが以下のように既知で F(ω)=∫f(t)*exp(-jωt)dt (ω=-∞,+∞) しかもF(ω)がWより高い周波数スペクトルを含まないなら F(ω)=0 (|ω|>2πW) ということになり、元の信号x(t)は以下の形で表すことができる f(t)=(1/2π)∫F(ω)*exp(jωt)dω (ω=-2πW,+2πW) これが帯域制限された信号の定義である。 ここでnを任意の整数として t=n/2W と置き換えると f(n/2W)=(1/2π)∫F(ω)*exp(jωn/2W)dω (ω=-2πW,+2πW) と表すことができる。 左辺は帯域制限された信号のサンプル値ということになる。 F(ω)は元の帯域制限されたf(t)のFourier変換そのものであるためf(t)とF(ω)の対応は一意的に決まり、上記のサンプル値もf(t)と一致する。 さってこっからどうすんだ? シャノンの論文では先の積分式はFourier係数そのものだからということを言っているのだが... サンプリングできることは当たり前で、あとはオリジナルのスペクトル形状(まだスペクトルという概念が一般的でなかった当時のナイキストはこれを"shape"と呼んでいる)が保存されているかどうかを確かめる必要がある。それには離散数列をFourier変換して周波数領域で確かめる必要がある。 いろいろ調べるとあるにはあるが困ったことに離散時間信号処理の本のδ(n)はFourier変換や解析学などの数学書に出てくるデルタ関数とは名前も性質もことなるものである点である。 デルタ関数は δ(t)=+∞ (t=0) =0 (t≠0) ∫δ(t)dt=1 と定義されるが有名なデジタル信号処理のバイブルで出てくる似たようなδを使用する単位サンプリング列は δ(n)=1 (n=0) =0 (n≠0) というものだ。無論後者を使えば簡単なのだが、シャノンの時代にはまだそんな概念はなかったから怪しい部分である。離散時間系では時間積分ができないのでデルタ関数では都合がわるいのである。 シャノンの論文では予め帯域制限された信号を扱うという前提なので、理想低域フィルタのshapeと信号の離散時間信号スペクトルの積を逆Fourier変換すれば元の信号が歪みなく再現できるということを言っているにすぎない。 こまったな。 検索すると同じ名前の統計学の理論が数多くヒットする。大きな母集団からどれだけの割合の数を抜き取り検査(サンプリング)すると母集団全体の性質を予測できるかというもの。これも同形の概念だけど、まったく別物なので注意。 調べていくと、どうやらサンプリング定理をどのように人に説明するかはその人の納得した理解方法によって様々であることがわかる。 ベル研の資料にもサンプリング定理が手短に触れられている、その内容は論文のその部分の趣旨を忠実に要約したものであった。それ以上の深入りや詮索はせずにおまえらはさっさと暗記しろという感じ。シャノンが教えたとおり憶えろという感じだ。 それと違って近代では、シャノンが書いたのとは異なる、おそらくそれで納得できなかったり、もっと広い観点でとらえなおそうと試みた結果、様々な解釈が生まれている。 それらの中でいくつか興味深い共通点があるものは、サンプル列の周波数スペクトルがオリジナルの信号のそれとどう違うかという点を納得ゆくように数学的に説明している点。共通してFourier級数やFourier変換と重要な関係のあるポアソンの和公式(Poisson's summation formula)というのを用いている。本当はFourier変換の性質でインパルス列のFourier変換対を解いてみれば、時間領域のインパルス列は周波数領域でもインパルス列になるというそれまで学んだFourier変換の諸性質には出てこなかった驚愕の事実が明らかになるのだが、難しいのか海外の資料には変換対表にのみ結果が掲載されている。その性質を知れば、離散点なサンプル列はオリジナル信号スペクトルを周波数領域上で周期化することがFourier変換の双対性と畳み込みの性質により予測できるのだった。日本でも進歩的な学校ではFourier変換の講義の最後にこのポアソン加公式とサンプリング定理を教えている。 このサンプリング定理をどう自分の納得ゆくように解釈し理解するかがこの章の卒業課題演習のようなものであると思ってそれを自分でもやってみよう。 といいつつ既にこの問題に取り組み始めて4日が経過している。ほとんど不眠不休(夜は横になっているが頭の中では考え続けているので寝ていないことになる)で体がガタガタになって本当に寝込んでしまった。 今朝になってようやくうまくいかない原因に気づいた。 この問題の最初の試練は、サンプリングして点になってしまうとFourier変換しようにも積分値が定まらないので不可積分であるということである。そもそもリーマンの積分条件である、ほとんどの区間で連続でなければならないという条件を満たしていない。ほとんどの区間で不連続だからだ。 そうなるとまず最初にすべきことは、サンプリング後のデータを連続関数として表す必要がある。 これにはDiracのデルタ関数にご登場願うことになる。そもそもデルタ関数は物理学で点電荷や質量点を数学的に扱うために連続関数(分布)に置き換える必要から考案されたものだ。離散時間関数もサンプル点以外は0を取る関数とすればほとんどの区間で連続という条件を満たすので積分が可能になる。 最初に気づけよ(;´Д`) しかし研究すればするほど連続時間系と離散時間系の境界領域の深遠さに驚愕する。ありとあらゆる分野とつながっていそうなところである。いずれにせよ自分で一端は納得した導出方法を見つけられたとしても、将来また立ち戻ってきそうなテーマではある。 数日立ち止まってしまったがそろそろ続きを n/2Wの間隔で並ぶインパルス列を s(t)=Σδ(t-n/2W) (n=-∞,+∞) であらわすとしよう。そうするとサンプリングされた離散信号は連続時間系で表すと x(t)=f(t)s(t) =f(t)Σδ(t-n/2W) =Σf(n/2W)δ(t-n/2W) ということになる。 またこのFourier変換は X(ω)=∫x(t)*exp(-jωt)dt =∫{f(t)s(t)}*exp(-jωt)dt =(F*S)(ω) =∫F(Ω)S(ω-Ω)dΩ とf(t)とs(t)に対するFourier変換の畳み込み積分になることが容易に想像がつく。 f(t)のFourier変換はF(ω)とすると、s(t)のFourier変換はどうなるのだろう? ここが一番立ち止まった原因なのだが、最初に準備としてデルタ関数のFourier変換を知る必要がある ∫δ(t)*exp(-jωt)dt =exp(-jω*0)*∫δ(t)dt =exp(-jω*0)*1 =1 ということなる。それではデルタ関数を時間軸上でシフトした場合にはどうなるか? ∫δ(t-t0)*exp(-jωt)dt =exp(-jωt0) ということになる。これは時間軸上の関数のシフトに関するFourier変換対の公式を用いている。そうせずにτ=t-t0と積分変数変換しても ∫δ(t-t0)*exp(-jωt)dt =∫δ(τ)*exp(-jω(τ+t0))dτ =exp(-jωt0)*∫δ(τ)dτ =exp(-jωt0)*1 =exp(-jωt0) ということになる。 従ってs(t)のFourier変換は S(ω)=∫s(t)*exp(-jωt)dt =∫Σδ(t-n/2W)*exp(-jωt)dt =Σ∫δ(τ)*exp(-jω(τ+n/2W))dτ =Σ∫δ(τ)*exp(-jωτ)*exp(-jωn/2W)dτ =Σexp(-jωn/2W)∫δ(τ)*exp(-jωτ)dτ =Σexp(-jωn/2W) ということとになる。なんだこれは? 再びここで凍り付いたわけだ(;´Д`) 上のFourier変換結果を三角級数に展開すると S(ω)=Σexp(-jωn/2W) =Σ(cos(ωn/2W)-j*sin(ωn/2W)) =Σ(cos(ωn/2W)-jΣsin(ωn/2W) =Σcos(ωn/2W) (n=0,+∞) +Σcos(-ωn/2W) (n=0,+∞) -cos(0) +jΣsin(ωn/2W) (n=0,+∞) +jΣsin(-ωn/2W) (n=0,+∞) -j*sin(0) =Σcos(ωn/2W)+Σcos(ωn/2W)-1 (n=0,+∞) +jΣsin(ωn/2W)-jΣsin(ωn/2W) (n=0,+∞) =2*Σcos(ωn/2W)-1 (n=0,+∞) ということになる。これはなんなんだ? MaximaでW=1,n=0,100,ω=-5,5で近似式をプロットしてみると wxplot2d([2*(sum(cos((n*o)/2),n,0,100))-1], [o,-5,5])$ 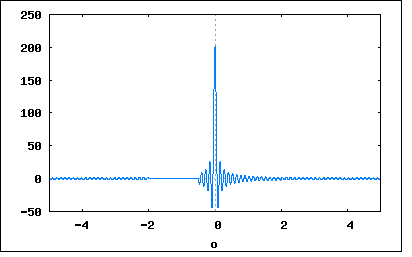 おお、なんかsinc関数ぽい(´∀` ) 今度はω=-50,50に範囲を広げてプロットしてみよう。 wxplot2d([2*(sum(cos((n*o)/2),n,0,100))-1], [o,-50,50])$ 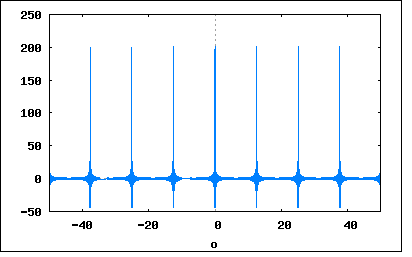 おお、インパルス列な感じ(´∀` ) ほんとのところどうなんだこれは?n=-∞,+∞にするとインパルス列に収束するのか? S(ω)=Σexp(-jωn/2W) (n=-∞,+∞) =2*Σcos(ωn/2W)-1 (n=0,+∞) =Σcos(ωn/2W) (n=-∞,+∞) =1+2Σcos(ωn/2W) (n=1,∞) は完全に偶関数のFourier級数の形をしているので、周期関数であることはまちがいない。 Σexp(-jωn/2W)がこんな三角級数展開になることは個人的には新発見である。 問題は S(ω)=Σexp(-jωn/2W) (n=-∞,+∞) =2*Σcos(ωn/2W)-1 (n=0,+∞) =Σcos(ωn/2W) (n=-∞,+∞) =1+2Σcos(ωn/2W) (n=1,∞) なる級数がインパルス列に収束するか、そしてそれはどういう式で表されるかという点である。 いよいよ核心部分に踏み込むことになる。 インパルス列はデルタ関数の総和で表すことができたが、今度はそのインパルス列のFourier変換もどうやらインパルス列になると予想される。これを証明するには、独立同分布の和が正規分布に収束するという統計学の中心極限定理(CLT:Central Limit Theorem)を用いることになる。 あちこちの文献を見ると、どうもサンプリング周期の逆数がFourier変換結果に入っているようなのだが、なんでだ? ちょっと前に書いた式の導出が怪しくなってきた、また猫味噌う(;´Д`) 一晩考えたがどうやら間違いはなさそうな気がする。 Fourier逆変換して検算してみると (1/2π)∫S(ω)*exp(jωt)dω =(1/2π)∫{Σexp(-jωn/2W)}*exp(jωt)dω =Σ(1/2π)∫exp(jω(t-n/2W))dω ここでτ=t-n/2Wと変数変換すると =Σ(1/2π)∫exp(jωτ)dω ここでデルタ関数のFourier変換対 δ(t) <=> 1 により δ(t)=(1/2π)∫exp(jωt)dω なので =Σδ(τ) =Σδ(t-n/2W) ということになるからである。 さて問題はインパルス列のFourier変換がどういったインパルス列になるかをどうやって導出するかという点である。 更によく検索で調べると、今回発見した Σcos(ωn/2W) (n=-∞,+∞) というのはディリクレ(Dirichlet)核といって、19世紀にディリクレが発見していたらしい。そういえばなんかの本で同じ波形を見た記憶が、その頃はなんの意味があるかわからなかった。 でディリクレ核は周期的に滑らかなデルタ関数に収束することが既に証明されているということもわかった。 でどうすればよいか。 一部の本では以下のFourier変換対が結果だけ示されている Σδ(t-nT) <=> (2π/T)Σδ(ω-n*(2π/T)) 求めていたのはこれなのだが、ではこれはどうやって導出するのか。 ひとつはPoisson summation formula Σf(t+nT) (n=-∞,+∞) =(1/T)ΣF(k/T)*exp(jn*(2π/T)*t) (n=-∞,+∞) ここでf(t)とF(x)はFoureir変換対 f(t) <=> F(x) である。 これを用いればすぐに Σδ(t-nT)=(1/T)Σexp(-jn*(2π/T)*t) ということがわかる。これをFourier変換すると ∫Σδ(t-nT)*exp(-jωt)dt =∫{(1/T)Σexp(-jn*(2π/T)*t)}*exp(-jωt)dt =(1/T)Σ∫exp(-jn*(2π/T)*t)*exp(-jωt)dt これは時間軸推移のFourier変換対 y(t)*exp(jω0*t) <=> F(ω-ω0) と直流1のFourier変換対 1 <=> 2πδ(ω) より 1*exp(jω0*t) <=> 2πδ(ω-ω0) であることから ∫Σδ(t-nT)*exp(-jωt)dt =(1/T)Σ∫exp(-jn*(2π/T)*t)*exp(-jωt)dt =(1/T)Σ2πδ(ω-n*(2π/T)) =(2π/T)Σδ(ω-n*(2π/T)) という結果が得られる。従って以下のFourier変換対が存在することが明らかである δ(t-nT) <=> (2π/T)Σδ(ω-n*(2π/T)) やったよママン(ノ∀`) 同じ結果を得るもうひとつの方法は、シャノンの論文でも用いられているFourier級数の性質を使う方法である、こちらの方が手順は短いがIQが低いと狐につままれたような気がしてならない。 その方法だと周期的に滑らかなデルタ関数は周期関数であるから以下のFourier級数で表すことができるという点から出発する Σδ(t-nT)=ΣCn*exp(jn*(2π/T)*t) ここでFourier係数Cnは Cn=(1/T)∫δ(t)*exp(-jn*(2π/T)*t)dt (t=-T/2,T/2) =(1/T)*exp(-jn*(2π/T)*0) =(1/T)*1 =1/T ということになり Σδ(t-nT)=Σ(1/T)*exp(jn*(2π/T)*t) (n=-∞,∞) =(1/T)Σexp(jn*(2π/T)*t) =(1/T)Σexp(-jn*(2π/T)*t) というPoisson summation formulaを用いたのと同じ結果が得られる。同じ結論を得るのにいくつもの方法がある良い例である。 さて周期インパルス関数(周期デルタ関数、Shah関数、くし型関数)のFourier変換がわかったので、いよいよサンプリングされた離散データ列のFourier変換を導くことにする。 サンプリングされた離散データ列は x(t)=f(t)s(t) =f(t)Σδ(t-nT) ここで T=1/2W で表すことができる。これのFoureir変換は X(ω)=∫x(t)*exp(-jωt)dt =∫f(t)s(t)*exp(-jωt)dt これは関数f(t),s(t)の積のFourier変換なので以下のFourier変換対 f(t)s(t) <=> (F*S)(ω) としてf(t),s(t)のそれぞれのFoureir変換F(ω),S(ω)との畳み込み積分になることが明らかである。 従って X(ω)=∫f(t)s(t)*exp(-jωt)dt =(F*S)(ω) =(1/2π)∫F(ω')S(ω-ω')dω' f(t)のFourier変換はF(ω)そのままでよいとしてインパルス列関数s(t)のFourier変換はさきほど導出した通り周波数領域でインパルス列関数になるので S(ω)=(2π/T)Σδ(ω-n*(2π/T)) これをX(ω)の式に代入すると X(ω)=(1/2π)∫F(ω')S(ω-ω')dω' =(1/2π)∫F(ω'){(2π/T)Σδ(ω-ω'-n*(2π/T))}dω' =(1/T)Σ∫F(ω')δ(ω-ω'-n*(2π/T))dω' =(1/T)ΣF(ω-n*(2π/T)) ということになる。 これは2π/Tの間隔で周期的にF(ω)のスペクトルが無限に繰り返していることを意味する。 ここで最初に与えられた帯域制限の条件(f(t)がWより大きな周波数スペクトルを持たない) F(ω)=0 (|ω|>2πW) を満たすなら、周期的なスペクトルは互いに重なり合わないので元の信号のスペクトルをそのまま保存することになる。 このためには T<1/2Wである必要がある。すなわち制限帯域周波数の2倍以上のレートで信号をサンプルする必要があることを意味する。 残るはサンプルされた離散データ列から元の信号を復元できるかという点。 以前の問題にあったような矩形周波数領域を持つ理想低域フィルタを通せば元の信号のスペクトルが通過することが明らかである。これは矩形領域のFourier逆変換とサンプルされた離散データ列との畳み込み積分に変換されることを意味する。すなわち f(t)=(x*r)(t) <=> X(ω)R(ω)=F(ω) ここで R(ω)=0 (|ω|>2πW) =1 (|ω|≦2πW) なる理想低域フィルタのスペクトル。そのFourier逆変換は r(t)=(1/2π)∫exp(jωt)dω (ω=-2πW,+2πW) =(1/2π){exp(j(2πW)t)/jt-exp(j(-2πW)t)/jt} =(1/2π){exp(j2πWt)/jt-exp(-j2πWt)/jt} =(1/2π){2*sin(2πWt)/t} =sin(2πWt)/πt 従って理想低域フィルタとサンプルされた関数スペクトルの積のFourier逆変換は f(t)=(1/2π)∫X(ω)R(ω)*exp(jωt)dω =(x*r)(t) =(1/T)Σf(n/2W)*sin(2πW(t-n/2W))/π(t-n/2W) =(1/T)Σf(n/2W)*sin(π(2Wt-n))/π(t-n/2W) T=1/2W なので f(t)=Σf(n/2W)*sin(π(2Wt-n))/π(2Wt-n) ということになり、sinc関数とサンプルデータの積の総和によって元の信号が復元されることが示される。 このような級数式はCardinal級数とよばれ古くから知られていたが、それが信号のデジタル化とその復元にかかわるものだという関係が示されたのはシャノンの時代になってからである。いろいろと歴史研究された中ではフランスの数学者であるCauchyがこのことを知っていたという説があるが、引用されているCauchyの論文には直接それに該当する記述は見あたらず謎のまま。Cauchy自身Fourier級数の収束に関して最初の論文を出しているので、あたらずとも遠からずの研究や思索はしていたと思われるが確たる証拠が無い。 ふう、数学の歴史をさかのぼって追体験するような問題だったが、とりあえず自分を納得させることは出来たので良しとしよう。まだ気になる点がいくつもあるが、それは追々。 これにて「詳解 電気回路演習 (上)」を読了。 引き続き「詳解 電気回路演習 (下)」に臨む。 |
| « 1 ... 5 6 7 (8) | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

