| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2007-11-11 23:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題77:温度補償抵抗回路 さてついに直流回路の最後の問題である。がいきなり自分なりに解こうと思ってはまった。
問題は3つの抵抗R1,R2,R3を図の様に接続した回路でR2に流れる電流I2が温度によらず一定になるには3つの抵抗の温度係数α1、α2,α3の関係はどうあらねばならないか導けというもの。 単純に考えるとこの回路全体の合成抵抗の温度係数αが0になるようなα1,α2,α3の関係を導けばいいのではないか。 しかし良く考えたらこれは正しくはない。全体に流れる電流が一定でもR2とR3に流れる電流の配分が変っているかもしれない。そうすると題意とは異なってしまう。 なのでやはり著者と同じようにR2に流れる電流I2に着眼してそれが温度変化にかかわらず一定に補償するためのα1,α2,α3の関係を導く必要がある。 簡単な話I2の式を図のそれぞれの抵抗の温度係数を考慮したものでたてて、それを温度で微分し、得られた微分係数が0となるようなα1,α2,α3の関係を見いだせば良いと思った。 I2=(E*R3*(α3*T+1))/(R2*R3*(α2*T+1)*(α3*T+1)+R1*R3*(α1*T+1)*(α3*T+1)+R1*R2*(α1*T+1)*(α2*T+1)) と表すことができるので、上の式をTで微分すればよい。 (%i75) diff((E*R3*(a3*T+1))/(R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T +1)*(a2*T+1)), T); (%o75) (a3*E*R3)/(R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T+1)*(a2*T+1))-(E*R3*(a3*T+1)*(a2*R2*R3*(a3*T+1)+a1*R1*R3*(a3*T+1)+a3*R2*R3*(a2*T+1)+a1*R1*R2*(a2*T+1)+a3*R1*R3*(a1*T+1)+a2*R1*R2*(a1*T+1)))/((R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T+1)*(a2*T+1))^2 とうことで数学公式の通りのものが出てきた。 問題はTで微分したはずだが微分係数にTが含まれているという点である。 なにか間違っているのだろうか? それぞれの抵抗値は温度によって変化する関数なので数学公式をあてはめても (g(x)/f(x))'=(g'(x)f(x)-g(x)f'(x))/(f(x))^2 ということで分母や分子には元の関数がそのまま現れることになる。 まあそれでも分子が0になる条件を見つければいいのだが、これで同じ結果が出るか謎である。 ちなみに姉妹本の「詳解 電磁気学演習」にもまったく同じ問題が出ているが、著者の解とは異なった表現の答えとなっているが基本的な解法は同じで原始関数である抵抗値R1,R2,R3は温度変化には依存しない定数として扱い、導関数を求める時のみ温度に依存している性質を利用している。 著書の解法は根本的に間違っているような気がするのだが。どうなのだろうか。 ちなみに自分で立てたI2の導関数を整理すると (%i84) factor(%); (%o84) -(E*R3*(a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2* a1*a2*R1*R2*T+a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2))/((a2*a3*R2*R3*T^2+a1*a3*R1*R3*T^2+a1* a2*R1*R2*T^2+a3*R2*R3*T+a2*R2*R3*T+a3*R1*R3*T+a1*R1*R3*T+a2*R1*R2*T+a1*R1*R2*T+R2*R3+R1*R3+R1*R2) ^2 となる。これの分子のTに依存しない要素だけ抜き出すと a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2 これが0となるa1,a2,a3の関係を求めると a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2=0 両辺をR1*R2*R3で割ると a2/R1+a1/R2-a3/R3+a2/R3+a1/R3=0 整理すると a2/R1+a1/R2+(a1+a2-a3)/R3=0 これは著者の解をR1*R2*R3で割って整理したものと同じである。 問題は自分の式で温度に依存する以下の部分である a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2*a1*a2*R1*R2*T これも0でなければならないから a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2*a1*a2*R1*R2*T=0 これを整理すると a3*T^2*(a2*a3*R2*R3+a1*a3*R1*R3+a1*a3*R1*R2)+2*T*(a2*a3*R2*R3+a1*a3*R1*R3+a1*a2*R1*R2)=0 ということになる。従って a2*a3*R2*R3+a1*a3*R1*R3+a1*a2*R1*R2=0 である必要がある。 R1*R2*R3で割ると a2*a3/R1+a1*a3/R2+a1*a2/R3=0 という関係もなりたたないといけないということになる。 これをa3で割ると a2/R1+a1/R2+a1*a2/(a3*R3)=0 これは先の温度に依存しない分子の項から求めた式と部分的に一致しているが最後の a1*a2/(a3*R3)が (a1+a2-a3)/R3とは違っているだけである。 両方の式を満足するには a2/R1+a1/R2+a1*a2/(a3*R3)=a1/R2+(a1+a2-a3)/R3+a2/R1=0 でなければならない すなわち a1*a2/a3=a1+a2-a3 という関係が成り立つ必要がある。 両辺にa3をかけると a1*a2=a1*a3+a2*a3-a3^2 つまり a3^2-a1*a3-a2*a3+a1*a3=0 因数分解できるので (a3-a1)*(a3-a2)=0 という関係が成り立てば良いということになる。 つまりa1=a2=a3なら条件を満たすということか? この考え方はあっているのだろうか? 実際にI2の式にa1=a2=a3としてみたとこで温度項が雲母に残ってしまう。ということでやはり自分の解法はどこか間違っているようだ。 著者の解が正しいかどうかI2の式に代入できる適当な温度係数の値を選ぼうとしてもR1,R2,R3が関係してくるので見つけるのが困難である。やるとするとR1,R2,R3が決まっていて温度係数のうちいずれか一つのみを未知数として関係式から残り1つの温度係数を解くしかないのかもしれない。 実際にやってみよう、R1=1000,R2=2000,R3=3000としてa1=0.01,a2=0.02とした場合に著者の条件を満たすa3を解くと [a3=21/200] という答えが出る。実際にこれらをI2の式に代入してみると (3*E*(21*T+200))/(10*(323*T^2+23100*T+220000)) 全然温度依存している。実際にTを変化させて電流をプロットしてみても 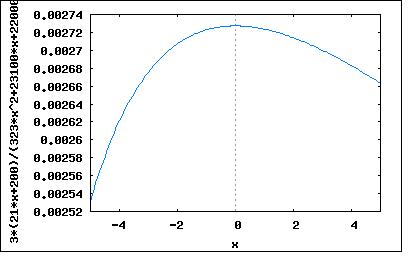 全然補償になっていない。 著者の解は単に一定の温度でI2が最大値を取る温度係数間の関係条件を示しているにすぎない。従って最大値付近では電流の温度変化は確かに少ないが温度によって電流が変化するのは変わらない。 最後の問題で後味を残すことになってしまったが、次ぎの交流回路理論に進むとしよう。 ちなみに温度補償回路はアナログ回路設計ではつきものであるので重要である。極めて短い時間でも回路に流れる電流が増加すれば消費電力が増加しそれが温度上昇を引き起こしそれによって電流が変化するというやっかいな問題が回路が高速になり微少になるにつれ顕在化してくる。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

