| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-12 22:05 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【50】対称三相交流ひずみ波 次ぎの問題は対称三相交流ひずみ波に関するもの。
三相起電力がともに対称で同形の波形で、単に1/3周期ずつ位相がずれている場合以下を証明せよというもの。 (1)基本波が対称三相起電力で (2)第三高調波は各相の大きさが同じであること (3)第五高調波が相回転の方向が基本波と逆の対称三相起電力で (4)第七高調波は基本波と相回転の方向が同じ対称三相起電力である 題意より三相起電力が対称波であることから、基本波と奇数次の高調波からなるひずみ波とみなすことができる。Fourier級数展開で表すと Ea=ΣEn*sin(nωt+θn) (n=1,∞) Eb=ΣEn*sin(nωt+θn-n*2π/3) (n=1,∞) Ec=ΣEn*sin(nωt+θn-n*4π/3) (n=1,∞) (1)基本波のみについて各相を比較すると Ea1=E1*sin(ωt+θ1) Eb1=E1*sin(ωt+θ1-2π/3) Ec1=E1*sin(ωt+θ1-4π/3) 従って基本波は対称三相交流そのものである。 (2)第三高調波について比較すると Ea3=E3*sin(3ωt+θ3) Eb3=E3*sin(3ωt+θ3-3*2π/3) =E3*sin(3ωt+θ3-2π) =E3*sin(3ωt+θ3) Ec3=E3*sin(3ωt+θ3-3*4π/3) =E3*sin(3ωt+θ3-4π) =E3*sin(3ωt+θ3) 従って第三高調波はすべて同相で同じ大きさである。 (3)第五高調波について調べると Ea5=E5*sin(5ωt+θ5) Eb5=E5*sin(5ωt+θ5-5*2π/3) =E5*sin(5ωt+θ5-10π/3) =E5*sin(5ωt+θ5-4π/3-2π) =E5*sin(5ωt+θ5-4π/3) Ec5=E5*sin(5ωt+θ5-5*4π/3) =E5*sin(5ωt+θ5-20π/3) =E5*sin(5ωt+θ5-2π/3-6π) =E5*sin(5ωt+θ5-2π/3) 従って第五高調波は基本波と逆送の対称三相交流である。 (4)第七高調波について調べると Ea7=E7*sin(7ωt+θ7) Eb7=E7*sin(7ωt+θ7-7*2π/3) =E7*sin(7ωt+θ7-14π/3) =E7*sin(7ωt+θ7-2π/3-4π) =E7*sin(7ωt+θ7-2π/3) Ec7=E7*sin(7ωt+θ7-7*4π/3) =E7*sin(7ωt+θ7-28π/3) =E7*sin(7ωt+θ7-4π/3-8π) =E7*sin(7ωt+θ7-4π/3) 従って第七高調波は基本波と同相の対称三相交流である。 |
| webadm | 投稿日時: 2009-9-12 22:23 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【51】対称三相交流ひずみ波(その2) 次ぎの問題は前問の続き。前問の第三高調波とその倍数の高調波が線間電圧に含まれないことを示せというもの。
前問で第三高調波は各相で同相となるということはわかったが、第七高調波以降はどうなるかというと m=3^n次の高調波の場合(n=1,∞) Eam=Em*sin(mωt+θm) Ebm=Em*sin(mωt+θm-m*2π/3) =Em*sin(mωt+θm-3^n*2π/3) =Em*sin(mωt+θm-1^n*2π) =Em*sin(mωt+θm) Ecm=Em*sin(mωt+θm-m*4π/3) =Em*sin(mωt+θm-3^n*4π/3) =Em*sin(mωt+θm-1^n*4π) =Em*sin(mωt+θm) 従って3^n次の高調波はすべて同相で同じ大きさであるので線間電圧の定義より3^n次の高調波に関する線間電圧成分は Eabm=Eam-Ebm=Em*sin(mωt+θm)-Em*sin(mωt+θm)=0 Ebcm=Ebm-Ecm=Em*sin(mωt+θm)-Em*sin(mωt+θm)=0 Ecam=Ecm-Eam=Em*sin(mωt+θm)-Em*sin(mωt+θm)=0 ということになり、線間電圧には3^n次の高調波成分は含まれないことになる。 |
| webadm | 投稿日時: 2009-9-12 23:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【52】対称三相交流ひずみ波(その3) 次ぎの問題は、対称三相交流ひずみ波の相電圧が第三高調波を含む場合、線間電圧の実効値は相電圧のそれの√3倍よりも小さいことを示せというもの。
第三高調波を含む対称三相交流ひずみ波を以下のようにFourier級数展開で表すと Ea=E1*sin(ωt+θ1)+E3*sin(3ωt+θ3) Eb=E1*sin(ωt+θ1-2π/3)+E3*sin(3ωt+θ3) Ec=E1*sin(ωt+θ1-4π/3)+E3*sin(3ωt+θ3) 線間電圧は Eab=Ea-Eb=E1*sin(ωt+θ1)+E3*sin(3ωt+θ3)-(E1*sin(ωt+θ1-2π/3)+E3*sin(3ωt+θ3)) =E1*(sin(ωt+θ1)-sin(ωt+θ1-2π/3)) =E1*2*cos((2ωt+2θ1-2π/3)/2)*sin((2π/3)/2) =2*E1*cos(ωt+θ1-π/3)*sin(π/3) =2*E1*cos(ωt+θ1-π/3)*(√3/2) =√3E1*cos(ωt+θ1-π/3) 従って線間電圧の実効値は |Eab|=√3|E1|/√2 一方相電圧の実効値は |Ea|=sqrt((|E1|/√2)^2+(|E3|/√2)^2) =(1/√2)*sqrt(|E1|^2+|E3|^2) 従って対称三相交流ひずみ波の線電圧と相電圧の実効値の比は |Eab|/|Ea|=(√3|E1|/√2)/(1/√2)*sqrt(|E1|^2+|E3|^2) =√3|E1|/sqrt(|E1|^2+|E3|^2) ここで第三高調波が含まれる場合|E3|>0なので |E1|/sqrt(|E1|^2+|E3|^2) < 1 従って実効値の比は√3倍よりも小さくなる。 |
| webadm | 投稿日時: 2009-9-13 0:08 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【53】対称三相交流ひずみ波(その4) 次ぎの問題は第三高調波を含む対称三相交流ひずみ波起電力と平衡三相4線式回路に関する問題。
各線電流を測定したところすべて同じ読みで |Ia|=|Ib|=|Ic|=|I| 中線の電流は|I0|だった場合、各相の基本波、第三高調波の電流を求めよというもの。 各相の電流をFourier級数展開で表すと Ia=I1*sin(ωt+θ1)+I3*sin(3ωt+θ3) Ib=I1*sin(ωt+θ1-2π/3)+I3*sin(3ωt+θ3) Ic=I1*sin(ωt+θ1-4π/3)+I3*sin(3ωt+θ3) 中線の電流はキルヒホッフの電流則により I0=Ia+Ib+Ic =I1*sin(ωt+θ1)+I3*sin(3ωt+θ3)+I1*sin(ωt+θ1-2π/3)+I3*sin(3ωt+θ3)+I1*sin(ωt+θ1-4π/3)+I3*sin(3ωt+θ3) =I1*(sin(ωt+θ1)+sin(ωt+θ1-2π/3)+sin(ωt+θ1-4π/3))+3*I3*sin(3ωt+θ3) =I1*(sin(ωt+θ1)+sin(ωt)*cos(2π/3)+cos(ωt)*sin(2π/3)+sin(ωt)*cos(4π/3)+cos(ωt)*sin(4π/3))+3*I3*sin(3ωt+θ3) =I1*(sin(ωt+θ1)*(1+cos(2π/3)+cos(4π/3))+cos(ωt)*(sin(2π/3)+sin(4π/3))+3*I3*sin(3ωt+θ3) =I1*(sin(ωt+θ1)*(1-1/2-1/2)+cos(ωt)*(√3/2-√3/2))+3*I3*sin(3ωt+θ3) =3*I3*sin(3ωt+θ3) 従って中点の電流は各相の第三高調波の三倍ということになる。 一方各相のひずみ波電流の実効値は基本波と高調波の実効値から |I|=sqrt(|I1|^2+|I3|^2) で表される。 ここで |I3|=|I0|/3 を代入すると |I|=sqrt(|I1|^2+(|I0|/3)^2) これより基本波の実効値は |I1|^2=|I|^2-(|I0|/3)^2 従って |I1|=sqrt(|I|^2-(|I0|/3)^2) ということになる。 |
| webadm | 投稿日時: 2009-9-13 3:02 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【54】対称三相交流ひずみ波(その5) 次ぎの問題は、前問のような対称三相回路ひずみ波電流が流れているときに中性線の有無による有効電力の相違を示せというもの。
中性線がある場合の有効電力は線間電圧と線電流より Pa=(1/T)∫pdt=(1/T)∫(ea*ia+eb*ib+ec*ic)dt =(1/T)∫((E1*sin(ωt+θ1)+E3*sin(3ωt+θ3))*(I1*sin(ωt+θ1+φ1)+I3*sin(3ωt+θ3+φ3))+(E1*sin(ωt+θ1-2π/3)+E3*sin(3ωt+θ3-3*2π/3))*(I1*sin(ωt+θ1-2π/3+φ1)+I3*sin(ωt+θ1-3*3π/3+φ3)+(E1*sin(ωt+θ1-4π/3)+E3*sin(3ωt+θ3-3*4π/3))*(I1*sin(ωt+θ1-4π/3)+I3*sin(3ωt+θ3-3*4π/3)))dt =(1/T)*(∫(E1*sin(ωt+θ1)+E3*sin(3ωt+θ3))*(I1*sin(ωt+θ1+φ1)+I3*sin(3ωt+θ3+φ3))dt+∫(E1*sin(ωt+θ1-2π/3)+E3*sin(3ωt+θ3))*(I1*sin(ωt+θ1-2π/3+φ1)+I3*sin(3ωt+θ3+φ3))dt+∫(E1*sin(ωt+θ1-4π/3)+E3*sin(3ωt+θ3))*(I1*sin(ωt+θ1-4π/3+φ1)+I3*sin(3ωt+θ3-3*4π/3+φ3))dt) =(1/T)*(∫(E1*I1*sin(ωt+θ1)*sin(ωt+θ1+φ1)+E3*I3*sin(3ωt+θ3)*sin(3ωt+θ3+φ3))dt+∫(E1*I1*sin(ωt+θ1-2π/3)*sin(ωt+θ1-2π/3+φ1)+E3*I3*sin(3ωt+θ3)*sin(3ωt+θ3+φ3))dt+∫(E1*I1sin(ωt+θ1-4π/3)*sin(ωt+θ1-4π/3+φ1)+E3*I3sin(3ωt+θ3)*sin(3ωt+θ3+φ3))dt) =(1/T)*(∫(1/2)*E1*I1(cos(-φ1)-cos(2ωt+2θ1))dt+∫(1/2)*E3*I3*(cos(-φ3)-cos(6ωt+2θ3))dt+∫(1/2)*E1*I1*(cos(-φ1)-cos(2ωt+2θ1-4π/3+φ1))dt+∫(1/2)*E3*I3*(cos(-φ3)-cos(6ωt+2θ3+φ3))dt+∫(1/2)*E1*I1*(cos(-φ1)-cos(2ωt+2θ1-8π/3+φ1))dt+∫(1/2)*E3*I3*(cos(-φ3)-cos(6ωt+2θ3+φ3))dt) =(3/2)*E1*I1*cos(φ1)+(3/2)*E3*I3*cos(φ3) ここで相電圧と線電流の実効値は E1=√2|E1| E3=√2|E3| I1=√2|I1| I3=√2|I3| であるのでそれぞれ代入すると Pa=3*|E1||I1|cos(φ1)+3*|E3||I3|cos(φ3) =3*(|E1|I1|cos(φ1)+|E3||I3|cos(φ3)) ということになる。 他方中性線が無い場合の有効電力は相間電圧と線電流から Pa=(1/T)∫pdt=(1/T)∫(eba*ib+eca*ic)dt =(1/T)∫((eb-ea)*ib+(ec-ea)*ic)dt =(1/T)∫(((E1*sin(ωt+θ1-2π/3)+E3*sin(3ωt+θ3))-(E1*sin(ωt+θ1)+E3*sin(3ωt+θ3)))*(I1*sin(ωt+θ1-2π/3+φ1)+I3*sin(3ωt+θ3+φ3))+((E1*sin(ωt+θ1-4π/3)+E3*sin(3ωt+θ3))-(E1*sin(ωt+θ1)+E3*sin(3ωt+θ3)))*(I1*sin(ωt+θ1-4π/3+φ1)+I3*sin(3ωt+θ3+φ3))))dt =(1/T)∫((E1*sin(ωt+θ1-2π/3)-E1*sin(ωt+θ1))*(I1*sin(ωt+θ1-2π/3+φ1)+I3*sin(3ωt+θ3+φ3))+(E1*sin(ωt+θ1-4π/3)-E1*sin(ωt+θ1))*(I1*sin(ωt+θ1-4π/3+φ1)+I3*sin(3ωt+θ3+φ3)))dt =(1/T)*(∫E1*I1*(sin(ωt+θ1-2π/3)-sin(ωt+θ1))*sin(ωt+θ1-2π/3+φ1)dt+∫E1*I1*(sin(ωt+θ1-4π/3)-sin(ωt+θ1))*sin(ωt+θ1-4π/3+φ1)dt) =(1/T)*(∫E1*I1*sin(ωt+θ1-2π/3)*sin(ωt+θ1-2π/3+φ1)dt-∫E1*I1*sin(ωt+θ1)*sin(ωt+θ1-2π/3+φ1)dt+∫E1*I1*sin(ωt+θ1-4π/3)*sin(ωt+θ1-4π/3+φ1)dt-∫E1*I1*sin(ωt+θ1)*sin(ωt+θ1-4π/3+φ1)dt) =(1/T)*(∫E1*I1*(1/2)*(cos(-φ1)-cos(2ωt+2θ1-4π/3+φ1))dt-∫E1*I1*(1/2)*(cos(2π/3-φ1)-cos(2ωt+2θ1-2π/3+φ1))dt+∫E1*I1*(1/2)*(cos(-φ1)-cos(2ωt+2θ1-8π/3+φ1))dt-∫E1*I1*(1/2)*(cos(4π/3-φ1)-cos(2ωt+2θ1-4π/3+φ1))dt) =(1/T)*(∫E1*I1*(1/2)*cos(φ1)dt-∫E1*I1*(1/2)*cos(2π/3-φ1)dt+∫E1*I1*(1/2)*cos(φ1)dt-∫E1*I1*(1/2)*cos(4π/3-φ1)dt =E1*I1*(1/2)*(2*cos(φ1)-cos(2π/3-φ1)-cos(4π/3-φ1)) =E1*I1*(cos(φ1)-(1/2)*cos(2π/3-φ1)-(1/2)cos(4π/3-φ1)) =E1*I1*(cos(φ1)-(1/2)*(cos(2π/3)*cos(φ1)+sin(2π/3)*sin(φ1))-(1/2)*(cos(4π/3)*cos(φ1)+sin(4π/3)*sin(φ1))) =E1*I1*(cos(φ1)-(1/2)*((-1/2)*cos(φ1)+(√3/2)*sin(φ1))-(1/2)*((-1/2)*cos(φ1)+(-√3/2)*sin(φ1))) =E1*I1*(cos(φ1)+(1/4)*cos(φ1)+(1/4)*cos(φ1)) =E1*I1*(3/2)*cos(φ1) =3*|E1||I1|cos(φ1) というわけで中性線が無いと、第三高調波分だけ有効電力が少なくなる。 式の整理の最後でsin(φ1)項が現れたときにはどうなるかと気が滅入ったが、ちょうど相殺されて消えてくれてほっとした。 |
| webadm | 投稿日時: 2009-9-13 4:13 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【55】対称三相交流ひずみ波(その6) 次ぎの問題は以下のような対称三相交流ひずみ波起電力の相間電圧を導けというもの。
各相の起電力は以下の様に表される e1=√2|E1|sin(ωt)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt) e2=√2|E1|sin(ωt-2π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-4π/3) e3=√2|E1|sin(ωt-4π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-2π/3) 従って相間電圧はそれぞれ e12=e1-e2 =√2|E1|sin(ωt)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt)-√2|E1|sin(ωt-2π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-4π/3) =√2*(|E1|*(sin(ωt)-sin(ωt-2π/3))+|E5|*(sin(5ωt)-sin(5ωt-4π/3))) =√2*(|E1|*2*cos((2ωt-2π/3)/2)*sin((2π/3)/2)+|E5|*2*cos((10ωt-4π/3)/2)*sin((4π/3)/2)) =√2*(|E1|*2*cos(ωt-π/3)*sin(π/3)+|E5|*2*cos(5ωt-2π/3)*sin(2π/3)) =√2*(|E1|*2*cos(ωt-π/3)*(√3/2)+|E5|*2*cos(5ωt-2π/3)*(√3/2)) =√6*(|E1|*cos(ωt-π/3)+|E5|*cos(5ωt-2π/3)) =√6*(|E1|*sin(ωt-π/3+π/2)+|E5|*sin(5ωt-2π/3+π/2)) =√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6)) e23=e2-e3 =√2|E1|sin(ωt-2π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-4π/3)-√2|E1|sin(ωt-4π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-2π/3) =√2*(|E1|*(sin(ωt-2π/3)-sin(ωt-4π/3))+|E5|*(sin(5ωt-4π/3)-sin(5ωt-2π/3))) =√2*(|E1|*2*cos((2ωt-6π/3)/2)*sin((2π/3)/2)+|E5|*2*cos((10ωt-2π)/2)*sin((-2π/3)/2)) =√2*(|E1|*2*cos(ωt-π)*sin(π/3)+|E5|*2*cos(5ωt-π)*sin(-π/3)) =√2*(|E1|*2*cos(ωt-π)*(√3/2)+|E5|*2*cos(5ωt-π)*(-√3/2)) =√6*(|E1|*cos(ωt-π)-|E5|*cos(5ωt-π)) =√6*(|E1|*sin(ωt-π+π/2)-|E5|*sin(5ωt-π+π/2)) =√6*(|E1|*sin(ωt-π/2)-|E5|*sin(5ωt-π/2)) =√6*(|E1|*sin(ωt-π/2)+|E5|*sin(5ωt+π/2)) e31=e3-e1 =√2|E1|sin(ωt-4π/3)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt-2π/3)-√2|E1|sin(ωt)+√2|E3|sin(3ωt)+√2|E5|sin(5ωt) =√2*(|E1|*(sin(ωt-4π/3)-sin(ωt))+|E5|*(sin(5ωt-2π/3)-sin(5ωt))) =√2*(|E1|*2*cos((2ωt-4π/3)/2)*sin((-4π/3)/2)+|E5|*2*cos((10ωt-2π/3)/2)*sin((-2π/3)/2)) =√2*(|E1|*2*cos(ωt-2π/3)*sin(-2π/3)+|E5|*2*cos(5ωt-π/3)*sin(-π/3)) =√2*(|E1|*2*cos(ωt-2π/3)*(-√3/2)+|E5|*2*cos(5ωt-π/3)*(-√3/2)) =√6*(-|E1|*cos(ωt-2π/3)-|E5|*cos(5ωt-π/3)) =√6*(-|E1|*sin(ωt-2π/3+π/2)-|E5|*sin(5ωt-π/3+π/2)) =√6*(-|E1|*sin(ωt-π/6)-|E5|*sin(5ωt+π/6)) =√6*(|E1|*sin(ωt-π/6+π)+|E5|*sin(5ωt+π/6-π)) =√6*(|E1|*sin(ωt+5π/6)+|E5|*sin(5ωt-5π/6)) ということになる。 もともと問題文と著者の図で用いられている記号が合っていないので、図の方にあわせた。 また著者の解答の相間電圧の式には誤記があり eab=eb-ec とあるのは eab=ea-eb とすべきである。 |
| webadm | 投稿日時: 2009-9-13 5:32 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【56】対称三相交流ひずみ波(その7) 次ぎの問題は前問のようなY形三相発電機の線間電圧の波形率および波高率を求めよというもの。
前問の続きのような問題なので、まず線間電圧は前問の解から e12=e1-e2=√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6)) e23=e2-e3=√6*(|E1|*sin(ωt-π/2)+|E5|*sin(5ωt+π/2)) e31=e3-e1=√6*(|E1|*sin(ωt+5π/6)+|E5|*sin(5ωt-5π/6)) 波形率の定義を思い出すと 波形率=実効値/平均値 であるので、e12の実効値と平均値をそれぞれ求めると |e12|=sqrt((√6|E1|)^2+(√6|E5|)^2) =√6*sqrt(|E1|^2+|E5|^2) 平均値は対称波なので半周期分を積分 e12ave=(2/T)∫e12dt (t=0,T/2) =(2/T)∫√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6))dt =(2√6/T)*(|E1|∫sin(ωt+π/6)dt+|E5|∫sin(5ωt-π/6)dt) =(2√6/T)*(|E1|√3T/2π+|E5|√3T/10π) =2√6*(|E1|√3/2π+|E5|√3/10π) =(√2√6/π)*(|E1|+|E5|/5) =(2√3/π)*(|E1|+|E5|/5) ということになる。 従って波形率は 波形率=√6*sqrt(|E1|^2+|E5|^2)/(2√3/π)*(|E1|+|E5|/5) ということになる。 一方波高率の定義は 波高率=最大値/実効値 なので最初に線間電圧の最大値を知る必要がある。 e12をtで微分すると d(e12)/dt=d(√6*(E1*sin(ωt+π/6)+E5*sin(5ωt-π/6))/dt =√6*(ω*E1*cos(ωt+π/6)+5ω*E5*cos(5ωt-π/6)) =√6ω*(E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)) 従って極大極小値をとるのは E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)=0 を満たすtである。 これどうやって解くんだ? この主の三角関数が式に出てくる方程式は三角方程式と呼ぶらしく、高校の数学で習うらしい。憶えてないぞ。 y=E1*cos(ωt+π/6) y=-5*E5*cos(5ωt-π/6) を同時に満たすtとyを求めるというふうに考えることもできる。その解にはy=0となるtもあり得る。それ以外のy≠0なtもあるだろう。 著者の解と違ったアプローチをしようと悩みまくっている。 思いついたのは 上の関数は元々は平面座標上の一次関数を三次元円筒曲面上に写像した3次元螺旋曲線をそれと並行な2次元平面に投影したものと考えることができる。なので元の一次関数に変換して考えれば二元連立方程式を解くだけで済むのではないか? という点である。恐ろしくやっかいなので現在考え中。 小休止して、基本波と5次高調波からなるひずみ波がどんな波形かプロットしてみると wxplot2d([sin(5*x-%pi/6)+sin(x+%pi/6)], [x,-5,5])$ 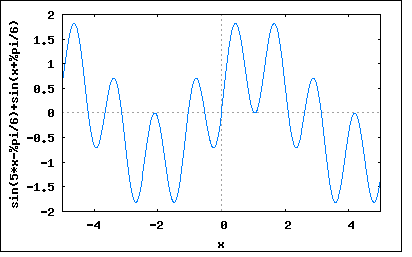 基本波の上に高調波が乗って波打っている、俗に言う「うなり」を生じている。基本波と高調波に微妙な位相のずれがあるので、最大値と最小値は基本波と高調波の最大振れの合計以内に収まる。 複雑な波形だが元は2つの正弦波からの合成である。半径の異なる2つの同心円筒曲面上に描かれた螺旋を極座標面で合成して得られる三次元曲線を平面に投影するとこうなる。2つの異なる周期を持つその三次元曲線を容易に想像することは難しい。ちょうど18世紀以前の天文学者達が天空球平面上で映し出される惑星の奇妙な軌跡から惑星の軌道を思い描くのに多大な年月を要したのと同じである。 さて少しこの問題を探ってみると、驚愕の事実が発覚。たまたまトイレでトイレットペーパーを交換しようとしたときにトイレットペーパーの芯に目をやったら、ちょうど良い具合に芯を構成する紙をつなぎ合わ境界線が二重螺旋を描いている。しかもひとつの螺旋はちょうど芯の両端で一周期になっている。芯の内側を見ると二重螺旋が現れるのは細長い同じ幅の紙のリボンを二重螺旋状にして接合しているためだとわかる。メーカーのロゴが印刷された独立した2つの同一幅の紙のリボンの螺旋がつなぎあわさって円筒が面が構成されている。これを設計したひとは数学が出来る人にちがいない。 更にトイレットペーパーの芯を眺めながら今回の三角方程式の解法を検討すると、それまで予想もしていなかった問題点を発見。螺旋状に巻かれた線を平面に展開すれば直線になるが、それだと二本の異なる螺旋をそれぞれ平面に展開した際の交点(連立方程式の根)はひとつしかない(根がひとつしかない)という疑問があった。しかしよく考えれば、円筒状の同一の螺旋へと写像される平面状の直線は無数にあるということに気づくべきだった。トイレットペーパーの芯を見てすぐにそれを直感した。ひとつの一次直線をある一定の等間隔(円筒の直径に相当する距離)で並行に無数に並べたものを円筒面に写像すると螺旋はたった一本しか現れない。ということは螺旋から平面への逆写像は多価性をもっているということのあらわれである。 そうすると二本のまったく異なる周期を持つ螺旋をそれぞれ平面に逆写像すると二種類の無数に並行する一次曲線の格子になる。従ってその交点は無数にある...orz ということで最初に考えたこのアプローチは従来的な三角方程式の解法と同じ結果を得るだろうと予測される。 一瞬超越関数である余弦関数を線形一次の代数方程式に逆変換できるとおもったのだが甘かった。しかしこれはなんとなく奥深い予感がするので、あせらずに時間をかけて研究したいテーマではある。 今しばらくはこの演習問題を解くのに専念しよう。 話を三角方程式にもどそう。 三角方程式というのは数学用語ではなくて日本独自の受験用語らしい。それも今日のように小子化時代では受験生から嫌われる数学は入学試験科目から外される傾向があるなか死語になりつつあるらしい。 三角方程式を解くにはベクトル図を描くとよいらしい。 E1*cos(ωt+π/6)+5*E5*cos(5ωt-π/6)=0 これを以下の様に書き換えると E1*cos(ωt+π/6)=-5*E5*cos(5ωt-π/6) この条件をベクトル図に描くと 図から 5*E5*cos(5ωt-π/6+π)=5*E5*cos(5ωt+5π/6) =-5*E5*cos(5ωt-π/6) ということがわかる。そこで θ=ωt+π/6 と置くと 5θ=5(ωt+π/6)=5ωt+5π/6 従って E1*cos(θ)-5*E5*cos(5θ)=0 ということになる。 どうすんだこれ。 とりあえずcos(5θ)を展開すると E1*cos(θ)-5*E5*cos(5θ) =E1*cos(θ)-5*E5*cos(2θ+3θ) =E1*cos(θ)-5*E5*(cos(2θ)*cos(3θ)-sin(2θ)*sin(3θ)) =E1*cos(θ)-5*E5*((2*cos(θ)^2-1)*(4*cos(θ)^3-3*cos(θ))-2*sin(θ)*cos(θ)*(-4*sin(θ)^3+3*sin(θ))) =E1*cos(θ)-5*E5*(8*cos(θ)^5-6*cos(θ)^3-4*cos(θ)^3+3*cos(θ)+8*sin(θ)^4*cos(θ)-6*sin(θ)^2*cos(θ)) =E1*cos(θ)-5*E5*(8*cos(θ)^5-10*cos(θ)^3+3*cos(θ)+8*cos(θ)^4*cos(θ)-6*sin(θ)^2*cos(θ)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*sin(θ)^4-6*sin(θ)^2+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*(1-cos(θ)^2)^2-6*(1-cos(θ)^2)+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8*(1-2*cos(θ)^2+cos(θ)^4)-6+6*cos(θ)^2+3)) =cos(θ)*(E1-5*E5*(8*cos(θ)^4-10*cos(θ)^2+8-16*cos(θ)^2+8*cos(θ)^4-6+6*cos(θ)^2+3)) =cos(θ)*(E1-5*E5*(16*cos(θ)^4-20*cos(θ)^2+5)) =cos(θ)*(E1-80*E5*cos(θ)^4+100*E5*cos(θ)^2-25*E5)) =0 従ってこれをcos(θ)について解くと cos(θ)=0 cos(θ)^2=-100*E5/2*(-80*E5)±sqrt((100*E5/2*(-80*E5))^2-(E1-25*E5)/(-80*E5)) =5/8±sqrt((5/8)^2+(E1/E5-25)/80) =5/8±sqrt(25/64+(E1/E5-25)/80) =5/8±(1/4)*sqrt(25/4+(E1/E5-25)/5) =5/8±(1/4)*sqrt((25+4*E1/E5)/20) =5/8±(1/8)*sqrt((25+4*E1/E5)/5) =5/8±(1/8)*sqrt(5+4*E1/5*E5) =(5±sqrt(5+4*E1/5*E5))/8 従って cos(θ)=sqrt(5±sqrt(5+4*E1/5*E5))/2√2 ということになる。 すなわち線間電圧e12が極大極小値をとるのは θ=±π/2 θ=±acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) ということになる(主値)。 線間電圧e12の二次導関数を求めると =d^2(e12)/dt^2 =d^2(√6*(|E1|*sin(ωt+π/6)+|E5|*sin(5ωt-π/6)))/dt^2 =-√6*ω^2*(|E1|*sin(ωt+π/6)+25*|E5|*sin(5ωt-π/6)) θ=ωt+π/6 と置くと d^2(e12)/dt^2 =-√6*ω^2*(|E1|*sin(θ)+25*|E5|*sin(5θ-π)) =-√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) ということになる。 θ=π/2を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(π/2)-25*|E5|*sin(5*π/2)) =-√6*ω^2*(|E1|-25*|E5|) θ=-π/2を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(-π/2)-25*|E5|*sin(-5*π/2)) =√6*ω^2*(|E1|-25*|E5|) 従って |E1|-25*|E5| > 0 の場合 すなわち |E1| > 25*|E5| の場合 θ=π/2で極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) =√6*(|E1|-|E5|) をとる。 逆に |E1|-25*|E5| < 0 の場合 すなわち |E1| < 25*|E5| の場合 θ=-π/2で極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) =√6*(|E5|-|E1|) ということになる。 同様に θ=±acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) の場合も θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) を代入すると d^2(e12)/dt^2=-√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) θ=-acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2) を代入すると d^2(e12)/dt^2=√6*ω^2*(|E1|*sin(θ)-25*|E5|*sin(5θ)) 従って |E1|*sin(θ)-25*|E5|*sin(5θ) > 0の場合 すなわち |E1|*sin(θ) > 25*|E5|*sin(5θ)の場合 θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)が極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) をとる。 |E1|*sin(θ)-25*|E5|*sin(5θ) < 0の場合 すなわち |E1|*sin(θ) < 25*|E5|*sin(5θ)の場合 θ=-acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)が極大値 e12p=√6*(|E5|*sin(5θ)-|E1|*sin(θ)) をとる。 ということになる。 またsin(θ),sin(5θ)ともにπ/2の場合に最大値1を取るため |E1| > 25*|E5| の場合 θ=π/2の極大値 e12p=√6*(|E1|-|E5|) が最大値となる。 他方sin(θ),sin(5θ)ともに-π/2の場合に最小値-1をとるため |E1| < 25*|E5| の場合 θ=acos(sqrt(5±sqrt(5+4*E1/5*E5))/2√2)の極大値 e12p=√6*(|E1|*sin(θ)-|E5|*sin(5θ)) が最大値となる。 従って波高率は上記の2つのケースについてそれぞれ |E1| > 25*|E5| の場合 波高率=最大値/実効値=e12p/|e12| =√6*(|E1|-|E5|)/√6*sqrt(|E1|^2+|E5|^2) =(|E1|-|E5|)/sqrt(|E1|^2+|E5|^2) |E1| < 25*|E5| の場合 波高率=最大値/実効値=e12p/|e12| =√6*(|E1|sin(θ)-|E5|*sin(5θ))/√6*sqrt(|E1|^2+|E5|^2) =(|E1|*sin(θ)-|E5|*sin(5θ))/sqrt(|E1|^2+|E5|^2) ということになる。 著者の解法によるθの式が異なるが、倍角の三角関数の公式より cos(θ)^2=(cos(2θ)+1)/2 ∴cos(θ)=sqrt((cos(2θ)+1)/2) 従って θ=acos(θ)=acos(sqrt((cos(2θ)+1)/2) これに著者のθの解を代入すると acos(θ)=acos(sqrt((cos(acos((1±sqrt(5+4E1/5E5))/4))+1)/2)) =acos(sqrt(((1±sqrt(5+4E1/5E5))/4)+1)/2)) =acos(sqrt((1/4±sqrt(5+4E1/5E5)/4)+1)/2)) =acos(sqrt((5/4±sqrt(5+4E1/5E5)/4)/2)) =acos(sqrt(5/8±sqrt(5+4E1/5E5)/8)) =acos(sqrt(5±sqrt(5+4E1/5E5))/2√2) 従って θ=±acos(sqrt(5±sqrt(5+4E1/5E5))/2√2) とこちらで求めたものと同一であることが確かめられる。 最初違う式が導かれたのでどっか間違っていないかくまなく調べたがこの検証で一安心した。 極大極小値と最大値最小値は意味が異なるので要注意だ。極大極小値は山と谷だがピークやボトムではない点に注意。 ふう、だいぶ長くかかったがこれで対称三相交流ひずみ波の問題は終了。あとはFourier変換に関する問題を残すのみ。 |
| webadm | 投稿日時: 2009-9-18 20:23 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【57】Fourier変換公式の導出 次ぎの問題は、理論のときにすでにやってしまったFourier級数の指数形式の式からFourier変換公式を導けというもの。
"Fourier変換と波形解析"のスレッドですでに古典的なRiemann積分の考え方に基づいてFourier級数の指数形式からFourier変換の公式を導出している。手短に導出するだけならそれで十分であるが適用範囲が厳密ではない。 今日的に厳密にFourier変換の式を裏付けるには、Lebesgue積分の考え方にもとづいてRiemann積分では扱えない広範囲なケースに関してもFourier変換が成り立つことを示す必要がある。 先のスレッドでも書いたが、Lebesgue積分を導入するには、沢山の数学的な準備が必要である。ほとんどそのお膳立てにページを割くことになり、結論的には同じ結果(Riemann積分可能ならLebesgue積分可能)を得るわけである。ただしRiemann積分可能な関数のFourier変換は必ずしもLebesgue積分可能な関数とはならないためRiemann積分でお茶を濁すしかなかった。また通常良く利用される離散Fourier変換ではこうした問題は無関係なため目をつぶっても構わない。 おそらく1966年にスエーデンの数学者Lennart Carlesonが証明する前に執筆されたFourier解析の書物はどれもこうした考え方に基づいていると思われる。すでに数学的な準備をし終えた人ならまだしも、古典的な数学の基礎とRiemann積分を理解した程度の初学者にはつらいものがある。Lebesgue積分では集合論や論理学の前提知識を要求されるのだから教える側も避けたいところだ。 といっても気になるので、Lebesgue積分の考えかたで検証してみよう。 とは言え実のところLebesgue積分の考え方でFourier変換を再構成している本はめったにお目にかからない。Lebesgue積分自体が説明がやっかいであるうえ、Riemann積分なら一行で説明できるところがLebesgue積分だと小冊子分かかってしまうからである。 もともとLebesgueが彼独特の積分の考え方を生み出したのも実のところFourier解析上の諸問題に関する真摯な取り組みからである。 従ってLebesgue積分を知るには彼の学位論文に立ち戻るのが最も早道からもしれない。後生の数学者の要約ではあまりに数学的な応用を意図するあまり元来の意図がまったく見えなくなってしまっている。そうした意味では数学が急速に発展していった19世紀にはまだLebesgueは登場しなかったので、ほとんどが古典的な求積法に基づく積分の考え方で凝り固まっている。しかし新しい積分の考え方でそれらを再構成するにはあまりにも影響範囲が広すぎるので、20世紀に入ってもそのまま再構成されることなく教えられている。 ちなみに学生の時にLebesgue積分を教わった記憶が無い。恥ずかしながら長い間Lbesgueを一般的な読み方とは違った読み方をしていたのは内緒だ。手元の共立出版の数学公式集にもLebesgue積分はおろか群論や論理学などの抽象数学にかんしては一切記載されていない。たぶんに初等数学もしくは古典的解析の範囲しか扱っていない。おそらく現在の学校のカリキュラムはゆとり化で更に範囲が狭まって内容も薄まっているに違いない。もしかして大学に入っても分数を知らない子もいるかもしれない。なにせ数学が試験科目に無いところもあるし。 個人的に興味のあるデジタル信号処理に限らず、最新の科学技術をキャッチアップするにはLebesgue積分の考え方を身につける必要がある。 このままいくと将来日本はハワイやニュージーランドと同じ様に観光地として生き残っていくしかないのかもしれない。土地開発は止めて自然をなるべく残すようにすればそれで生き残っていけるかもしれない、ゼネコンやセメント会社は消滅するかもしれないけど。人工が4分の3に減ればその分CO2排出量も減って25%削減は達成できるだろうし。 話を元に戻そう。 昨日注文してあった「ルベーグ 積分:長さおよび面積」共立出版が届いた。  在庫があったのですぐに届けられた。新品である。共立出版の「現代数学の系譜」シリーズの3巻目にあたり、監修者のことばには「最近、数学がとみに時代の脚光を浴びるようになった。現代社会による数学の役割がいちじるしく拡大されてきたのである。...」 いったい何時の話だろう、と思ったら初版は40年前であり、手元にあるのは1996年に増刷されたものらしい。  はしがきにあるように、Lebesgueの学位論文の翻訳そのものである。これを受理されるまで紆余曲折があったらしい、その間にいくつもの編が追加されている。最初に書かれたのがLebesgue積分そのものである。  論文の序文を見るととても明瞭にその目的が述べられている。後生の数学者の要約ではすっかり省かれてしまっている部分である。ここを読み飛ばしてしまってはなんのことは着いていけないに違いない。 本文の方は、今日見られるLebesgue積分の概要よりももっと具体的な例をあげた説明がなされていてむしろわかり易い感じがする。 以前に別のスレッドで紹介した、Riemann論文集に、Riemann積分が登場する論文も掲載されている。もともとはRiemannがゲッチンゲン大学で教授資格試験のために用意した3つのテーマのうち2番目のものでFourier級数に関するものである。以下がその部分、  Fourier級数の収束の問題を扱うのに積分の定義と適用範囲を伝統的な暗黙の了解のままにしておけないためRiemannが初めて可積分の条件を定義したのである。もともとの論文の目的はそれではないのだが、歴史的に積分可能性の定義をしたのはRiemannが初めてということになった。ゲッチンゲン大学での試験講義ではこれは採択されずガウスのたっての希望で3番目のテーマについて講義することになった。この論文はそれでお蔵入りになるはずだったが、Riemannの没後にRiemann夫人の願いで論文集として日の目を見ることになったといういきさつがある。そうでもなければRiemann積分という言葉も歴史上あり得なかったかもしれない。 Riemann積分は可積分の条件を初めて与えただけで、目的はそれ以外にあったので、厳密で拡張性のあるものではなかった。依然として解析学の世界では古典的な求積法の暗黙の了解が支配的であることには変わりなかった。これが今日も微積分を習うと、ニュートン・ライプニッツ以来から受け継がれている積分の概念をたたき込まれる理由である。 Lebesgueの論文の序文にあるように、こうした問題をジョルダンも早くから指摘していた。しかしジョルダンはそれに代わる新しい積分の概念を提案することはしなかったので、Lebesgueがそれを引き継いだとも言える。Lebesgueは新しい積分を集合の測度(オリジナル仏語mesure、英語のmeasureと同じ意を日本語訳した数学用語、線分の長さを測る巻き尺のメジャーや液体の容積を量る計量カップのメジャーと同じ意味だと個人的には勝手に解釈している)という考えをベースに定義している。線分の長さや平面の面積、三次元の体積などを点集合として扱い、集合の測度を定義することによって線分の長さ、平面の面積、立体の体積にとどまらずn次元への拡張を可能とするものである。 やはりLebesgue積分を知る上ではこの論文は必読だろう。 以前に別のスレッドで紹介した高木貞治の「解析概論 改訂第三版」ではLebesgue積分が追加されている。  後生の数学者のLebesgue積分の扱い方はどれも共通して集合の測度に関する理論の説明に大半の紙面を割いている。これが難解な理由かもしれない。最初これを読んでいたら数日で激しく鬱に襲われたのは言うまでもない。近代物理学や量子物理とかでもLebesgue積分は必修で、頭を悩ませる人が絶えないかもしれない。いたるところでLebesgue積分がツールとして使用されるので、知らないとついていけないのだ。そうした物理数学の本でもLebesgue積分の理論は難しいから定理だけをさっと紹介しているに留まっている。実際に応用するにはやはり本質的な理解が必要だろう。測度とか集合記号が出てきたら前提としてLebesgue積分の理解が必要と思って間違いないだろう。 かなり脇道にそれた感が否めないが、本題に戻ろう。 題意としては既に理論のところで証明している周期関数のFourier級数の複素形式 y(t)=ΣAn*exp(jnωt) An=(1/T)∫y(t)*exp(-jnωt)dt を非周期関数のFourier変換及び逆変換 y(t)=(1/2π)∫F(ω)*exp(jωt)dω F(ω)=∫y(t)*exp(-jωt)dt に拡張せよというもの。 Riemann積分の考え方では、最初のAnの式をy(t)の式に代入して変数変換や区間変換を施すことによって最終的にRiemann和の形にすることでFourier逆変換の式が得られる。元のFourier係数に相当する積分から変化した式をFourier変換の式と置くと最終的な式が得られる。 これと同じ結果をLebesgue積分の考え方で得るにはまだ時間が必要である。これは個人的な宿題とするのと同時に読者の課題としよう(´∀` ) こういった問題を解くだけでも学位論文になりそうなテーマが他にもごろごろしてそうである。数学者は突っ込まれそうなところはなるべく隠す傾向があるので、そういったところをほじくりだして解くだけでも論文のネタは尽きない。それが世の中や後生に役立つかどうかは別として実力の証明にはなる。 なので当面は後続する問題のクリアに集中しよう。 後日この問題に関してなんらかの進展があれば、ここに追記するなり、返信の形で掲載することにする。 |
| webadm | 投稿日時: 2009-9-22 22:54 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【58】Fourier変換の対称性 Fourier変換の諸性質を学んだ際に出てきた対称性(ωとtを取り替えたらどうなるか?)についての問題。
既に以下の記事で解いてしまっているので割愛する。 Fourier変換の諸性質 対称性というのが何のことを言っているのか理解するのが最も難しい点である。 |
| webadm | 投稿日時: 2009-9-22 23:02 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
【59】Fourier変換の時間軸の伸縮 次ぎの問題はFourier変換の諸性質の中で時間軸をのばしたり縮めたりした場合に変換対にどういう変化が現れるか導けというもの。
これも前掲の Fourier変換の諸性質 でやってしまっているので割愛する。 伸縮の係数は正だけでなく負もある。負の場合には波形を左右裏返しにすることを意味する。 |
| « 1 ... 3 4 5 (6) 7 8 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

