| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-5 7:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【37】RLC直列回路に流れる電流と電圧 次ぎの問題は少しひねったもの。
RLC直列回路に以下の様なひずみ波電流が流れるために必要な電圧を求めよというもの。 i=I1*sin(ωt)+I2*sin(2ωt+θ) いきなりこれだとわけがわからないが、基本波と高調波それぞれに対応する定電流源がRLC直列回路と並列に接続されている等価回路を想像すれば答えは自ずと得られる。 線形回路網の重ね合わせの理で、RLC直列回路に対して基本波と高調波のそれぞれの定電流源によって生じる電圧降下を合成すれば等価電圧源の式が得られるはずである。 便宜上基本波と高調波の定電流源、及びRLC直列回路のインピーダンスをそれぞれ極座標標記に直してそれぞれの電圧降下を求めると e1=I1*exp(jωt)*(R+j(ωL-1/ωC)) =I1*exp(jωt)*sqrt(R^2+(ωL-1/ωC)^2)*exp(jφ1) =I1*sqrt(R^2+(ωL-1/ωC)^2)*exp(j(ωt+φ1)) ここで φ1=atan((ωL-1/ωC)/R) e2=I2*exp(j(2ωt+θ))*(R+j(2ωL-1/2ωC)) =I2*exp(j(2ωt+θ))*sqrt(R^2+(2ωL-1/2ωC)^2)*exp(jφ2) =I2*sqrt(R^2+(2ωL-1/2ωC)^2)*exp(j(2ωt+θ+φ2)) ここで φ2=atan((2ωL-1/2ωL)/R) 従って電圧は e=e1+e2 =I1*sqrt(R^2+(ωL-1/ωC)^2)*exp(j(ωt+φ1))+I2*sqrt(R^2+(2ωL-1/2ωC)^2)*exp(j(2ωt+θ+φ2)) =I1*sqrt(R^2+(ωL-1/ωC)^2)*(cos(ωt+φ1)+j*sin(ωt+φ1))+I2*sqrt(R^2+(2ωL-1/2ωC)^2)*(cos(2ωt+θ+φ2)+j*sin(2ωt+θ+φ2)) 従って等価電圧源の正弦波標記は上の式の虚数部から得られ e=I1*sqrt(R^2+(ωL-1/ωC)^2)*sin(ωt+φ1)+I2*sqrt(R^2+(2ωL-1/2ωC)^2)*sin(2ωt+θ+φ2) ということになる。 著者の解も考え方としてはほぼ一緒で、既に知られているRLC直列回路のインピーダンスの絶対値と偏角の公式から同じ結果を得ている。 P.S 等価回路図でうっかりして定電流源を電圧源の記号を使って描いてしまっているのに気づいて図を修正した。 |
| webadm | 投稿日時: 2009-9-4 6:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【36】ひずみ波の検波値 次ぎの問題は題意がつかみづらいひずみ波の検波値に関するもの。
「第二高調波を含むひずみ波を二乗特性をもつ整流器で検波しようとした場合に、被測定端子を反転すると、検波値が元の値と異なることを示し、第三高調波のみを含む場合についても考察せよ。」 これだと何を言っているのかピンとこない。だいたい被測定端子ってどこだということすら説明されていない。 よく吟味すると以下の図のような感じだろうと想像する。いわゆる一石ゲルマラジオと一緒である。 ここで題意に従って第二高調波のみを含む場合 Em1≠0 Em2≠0 Em3=0 とすればよい。 wxplot2d([sin(2*x+%pi/6)+sin(x)], [x,-5*%pi,5*%pi])$ 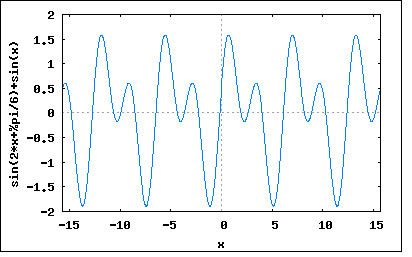 このケースではひずみ波は対称波ではなくなる(対称波となるには奇数次の高調波のみでなければならない)。 従ってひずみ波の正と負の波形は異なるため被測定端子を反対にした場合にはいずれにせよ出力波形は同じにならない。 一方第三高調波のみを含む場合は Em1≠0 Em2=0 Em3≠0 wxplot2d([sin(3*x+%pi/6)+sin(x)], [x,-5*%pi,5*%pi])$ 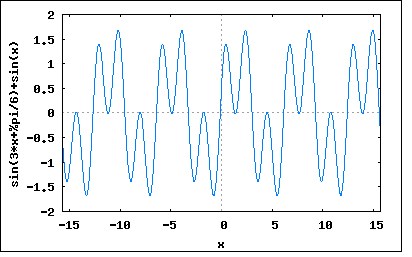 ということで、この場合はひずみ波は対称波となり、正と負側の波形は対称であるため、被測定端子を反対にしても検波出力は同じということになる。 これで十分だが、もっと定量的に示すにはどうどうすればいいのだろうか。 著者の解では第二高調波のみの場合に関しては同じような趣旨で非対称波だから同じにならないとしているが第三高調波のみの場合には瞬時値の式を符号反転したものと位相をπだけ進めた式が等しいことから同じ波形になるとしている。しかし同じことを第二高調波のみを含む場合に適用しても同じ結果が導き出されてしまうのだが e=Em1*sin(ωt)+Em2*sin(2ωt+θ2) -e=-Em1*sin(ωt)-Em2*sin(2ωt+θ2) =Em1*sin(ωt+π)+Em2*sin(2ωt+θ2+π) なので著者の説明では不十分である。対称波かどうか調べるには y(t+T/2)=-y(t) を満たすかどうかを調べれば良い。 これを適用すると e(t+T/2)=Em1*sin(ω(t+T/2))+Em2*sin(2ω(t+T/2)+θ2) =Em1*sin(ωt+ωT/2))+Em2*sin(2ωt+θ2+ωT) ここで ωT=2π を代入すると e(t+T/2)=Em1*sin(ωt+π)+Em2*sin(2ωt+θ2+2π) =-Em1*sin(ωt)+Em2*sin(2ωt+θ2) 従って e(t+T/2)≠-e(t) ということになり、非対称波であることが確かめられた。 一方第三高調波のみを含む場合 e(t+T2/)=Em1*sin(ω(t+T/2))+Em3*sin(3ω(t+T/2)+θ3) =Em1*sin(ωt+ωT/2)+Em3*sin(3ωt+θ3+3ωT/2) ここで ωT=2π を代入すると e(t+T/2)=Em1*sin(ωt+π)+Em3*sin(3ωt+θ3+3π) =-Em1*sin(ωt)-Em3*sin(3ωt+θ3) =-e(t) ということになる。従って対称波の条件を満足する。 P.S 著者の解では整流出力が|e|^2に比例するとしているが、これだと題意がかなり違ってしまうことになる。半波整流ではなく全波整流という意味になる。 これだと第二高調波のみを含む場合でも被測定端子を反転しても整流出力は同じになってしまう。 wxplot2d([abs(sin(2*x+%pi/6)+sin(x))], [x,-5*%pi,5*%pi])$ 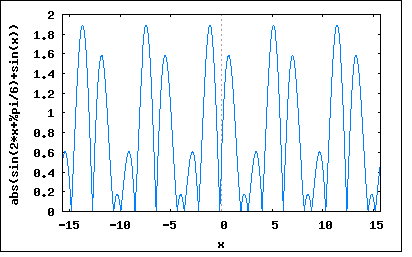 これでは著者の解答と違った結果になってしまうので、おそらく題意としては検波器は半波整流器を意味していると解釈するのが当然だろう。もちろんそうでなければ問題文そのものも変更しなければならなくなる。 P.S 2 もうひとつの考察方法としては、基本波と高調波それぞれの半波整流波形のFourier級数展開を導いて、その合成として整流波形のFourier級数展開を求めて正と負で対称かどうかを調べる方法もあるが、面倒なので読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2009-9-1 11:38 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【35】台形波の波形率と波高率 次ぎの問題は以下のような台形波の波形率と波高率を求めよというもの。
波形を式で表すと e=(A/(π/3))t (0≦t≦π/3) =(3*A/π)*t (0≦t≦π/3) =A (π/3≦t≦2π/3) =A-(A/(π/3))*(t-2π/3) =A-(3*A/π)*(t-2π/3) =A-(3*A/π)t+2*A =3*A-(3*A/π)t =3*A*(1-t/π) =(3*A/π)*(π-t) (2π/3≦t≦π/2) これは0〜πまでの区間しか示されていないのでその区間内での波形率と波高率を求めるしかない。 波形率は実効値と平均値の比であるから 波高率=実効値/平均値 =sqrt((1/π)∫y(t)^2dt)/(1/π)∫y(t)dt (0≦t≦π) =sqrt((2/π)∫((3*A/π)*t)^2dt (0≦t≦π/3) +(2/π)∫A^2dt (π/3≦t≦π/2) )/((2/π)∫(3*A/π)*tdt (0≦t≦π/3) +(2/π)∫Adt) (π/3≦t≦π/2) =sqrt((2/π)*(π*A^2/9)+(2/π)*(π*A^2/6))/((2/π)*(π*A/6)+(2/π)*(π*A/6)) =sqrt(2*A^2/9+2*A^2/6)/(2*A/6+2*A/6) =sqrt(2/9+1/3)/(4/6) =6*sqrt(5/9)/4 =2*sqrt(5)/4 =sqrt(5)/2 =1.12 波高率は最大値と実効値の比なので 波高率=最大値/実効値 =A/sqrt((1/π)∫y(t)^2dt) (0≦t≦π) =A/sqrt((2/π)∫((3*A/π)*t)^2dt (0≦t≦π/3) +(2/π)∫A^2dt) (π/3≦t≦π/2) =A/sqrt((2/π)*(π*A^2/9)+(2/π)*(π*A^2/6)) =A/sqrt(2*A^2/9+2*A^2/6) =1/sqrt(2/9+1/3) =1/sqrt(5/9) =3/sqrt(5) =1.34 ということになる。 あやうく繰り返し波形だと思いこみしてFourier級数展開を導こうとしてはまった。 |
| webadm | 投稿日時: 2009-9-1 10:45 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【34】リアクタンスに流れるひずみ波電流と電圧のひずみ率 次ぎの問題はリアクタンスに以下のひずみ波電流が流れる場合、その電圧と電流のひずみ率を比較せよというもの。
i=I1*sin(ωt)+I3*sin(3ωt) 著者と同じ解き方だと面白くないので、へそ曲がりな方法でやってみよう。 以前の様に線形回路網の重ね合わせを使うと 基本波と高調波のそれぞれの定電流電源に関してリアクタンスによる電圧降下の実効値を求めれば良いことになる。 リアクタンスがキャパシタンスCの場合 X1=1/ωC |X1|=sqrt(X1^2) =1/ωC X3=1/3ωC |X3|=sqrt(X3^2) =1/3ωC 従ってそれぞれの電圧降下の実効値は |E1|=|I1||X1| =(I1/√2)*(1/ωC) =I1/√2ωC |E3|=|I3||X3| =(I3/√2)*(1/3ωC) =I3/3√2ωC 電圧の歪み率keは ke=sqrt(|E3|^2)/|E1| =sqrt((I3/3√2ωC)^2)/(I1/√2ωC) =(I3/3√2ωC)/(I1/√2ωC) =I3/3*I1 電流の歪み率kiは ki=sqrt(|I3|^2)/|I1| =sqrt((I3/√2)^2)/(I1/√2) =(I3/√2)/(I1/√2) =I3/I1 従って電圧の歪み率は電流の歪み率の1/3ということになる。 同様にリアクタンスがインダクタンスLの場合 X1=ωL |X1|=sqrt(X1^2) =ωL X3=3ωL |X3|=sqrt(X3^2) =3ωL 従って電圧のひずみ率は ke=sqrt(|E3|^2)/|E1| =sqrt((I3||X3|)^2)/(|I1||X1|) =(|I3||X3|)/(|I1||X1|) =((I3/√2)*3ωL)/((I1/√2)*ωL) =3*I3/I1 電流のひずみ率は ki=sqrt(|I3|^2)/|I1| =|I3|/|I1| =(I3/√2)/(I1/√2) =I3/I1 従ってインダクタンスの場合は電圧のひずみ率は電流のひずみ率の3倍になる。 P.S 当初の掲載した等価回路図は定電流源が直列に接続されていたが、あきらかにそれは誤りであった。並列にしたものに改めた。 |
| webadm | 投稿日時: 2009-9-1 10:14 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【33】非線形回路とひずみ波 次ぎの問題は捻ってあって、いきなり以下の電圧電流特性を有する非線形回路に正弦波電圧を加えた場合の出力電流のひずみ率を計算せよというもの。
i=a1*e+a2*e^2 e=Em*sin(ωt) 従って流れる電流は i=a1*Em*sin(ωt)+a2*(Em*sin(ωt))^2 =a1*Em*sin(ωt)+a2*(Em^2*sin(ωt)^2) =a1*Em*sin(ωt)+a2*Em^2*(1/2-cos(2ωt)/2) =a2*Em^2/2+a1*Em*sin(ωt)-(a2*Em^2/2)*cos(2ωt) ということになる。 したがってそのひずみ率は ひずみ率=sqrt((a2*Em^2/2)^2)/(a1*Em) =(a2*Em^2/2)/(a1*Em) =a2*Em/2*a1 ということになる。 |
| webadm | 投稿日時: 2009-9-1 9:55 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【32】ひずみ波のひずみ率 次ぎは以下のひずみ波電流のひずみ率を計算する問題。
i=30*sin(ωt)+10*cos(3ωt)+5*sin(5ωt) ひずみ率は高調波の実効値の基本波の実効値の比なので ひずみ率=sqrt(|I3|^2+|I5|^2)/|I1| =sqrt((10/√2)^2+(5/√2)^2)/(30/√2) =sqrt(10^2+5^2)/30 =sqrt(125)/30 =sqrt(5)/6 =0.373 ということになる。 |
| webadm | 投稿日時: 2009-8-31 12:27 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【31】RLC混成回路とひずみ波の電流と電力 次ぎの問題は少し複雑な回路に以下のひずみ波電圧を加えた場合に各部を流れる電流と全体の電力を求めよというもの。
e=Em*(sin(ωt)+h*sin(3ωt)) 以前の問題と同様に線形回路の重ね合わせによって求めることができそうである。 最初にRLC混成回路の基本波、高調波それぞれに対するインピーダンスを求める。 Z1=jωL+1/(1/R+jωC) =jωL+(1/R-jωC)/((1/R)^2+(ωC)^2) =(1/R)/((1/R)^2+(ωC)^2)+j(ωL-ωC/((1/R)^2+(ωC)^2)) =R/(1+(ωCR)^2)+jω(L-CR^2/(1+(ωCR)^2)) |Z1|=sqrt(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2) Z3=3jωL+1/(1/R+3jωC) =3jωL+(1/R-3jωC)/((1/R)^2+(3ωC)^2) =(1/R)/((1/R)^2+(3ωC)^2)+3j(ωL-ωC/((1/R)^2+(3ωC)^2)) =R/(1+(3ωCR)^2)+3jω(L-CR^2/(1+(3ωCR)^2)) |Z3|=sqrt(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2) 従って全体を流れる電流の実効値は基本波と高調波のそれぞれの電流の実効値から |I|=sqrt(|I1|^2+|I3|^2) =sqrt(((Em/√2)/|Z1|)^2+((Em*h/√2)/|Z3|)^2) =sqrt((Em/√2)^2/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+(Em*h/√2)^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)) =(Em/√2)*sqrt(1/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)) ということになる。これはLに流れる電流の実効値でもある。 RとCに流れる電流は基本波、高調波それぞれに関してそれぞれ以下の関係が成り立つ I1=IR1+IC1 IR1*R=IC1*(1/jωC) これをIR1とIC1に関する2元連立方程式として解くと (%i57) e1:I1=IR1+IC1; (%o57) I1=IR1+IC1 (%i58) e2:IR1*R=IC1*(1/(%i*o*C)); (%o58) IR1*R=-(%i*IC1)/(o*C) (%i59) solve([e1,e2],[IR1,IC1]); (%o59) [[IR1=-(%i*I1)/(o*C*R-%i),IC1=(o*C*I1*R)/(o*C*R-%i)]] IR1=-jI1/(ωCR-j) =I1/(1+jωCR) IC1=ωCR*I1/(ωCR-j) =jωCR*I1/(1+jωCR) 従ってそれぞれの実効値は |IR1|=|I1|/sqrt(1+(ωCR)^2) =(Em/√2)/sqrt(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2))*sqrt(1+(ωCR)^2) |IC1|=|I1|*ωCR/sqrt(1+(ωCR)^2) =(Em/√2)*ωCR/sqrt(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2))*sqrt(1+(ωCR)^2) 同様に高調波についても |IR3|=|I3|/sqrt(1+(3ωCR)^2) =(Em*h/√2)/sqrt(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2))*sqrt(1+(3ωCR)^2) |IC3|=|I3|*3ωCR/sqrt(1+(3ωCR)^2) =(Em*h/√2)*3ωCR/sqrt(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2))*sqrt(1+(3ωCR)^2) 従ってRとCを流れる電流の実効値はそれぞれ |IR|=sqrt(|IR1|^2+|IR3|^2) =sqrt(((Em/√2)/sqrt(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2))*sqrt(1+(ωCR)^2))^2+((Em*h/√2)/sqrt(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2))*sqrt(1+(3ωCR)^2) )^2) =(Em/√2)*sqrt((1/(R^2/(1+(ωCR)^2)^2+ω^2/(L-CR^2/(1+(ωCR)^2))^2)*(1+(ωCR)^2)+h^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)*(1+(3ωCR)^2)) |IC|=sqrt(|IC1|^2+|IC3|^2) =sqrt(((Em/√2)*ωCR/sqrt(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2))*sqrt(1+(ωCR)^2))^2+((Em*h/√2)*3ωCR/sqrt(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2))*sqrt(1+(3ωCR)^2))^2) =(Em/√2)*sqrt((ωCR)^2/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)*(1+(ωCR)^2)+h^2*(3ωCR)^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)*(1+(3ωCR)^2)) ということになる。 一方消費電力は Pa=|E1||I1|cosφ1+|E3||I3|cosφ3 =(Em/√2)*((Em/√2)/|Z1|)*Real(Z1)/|Z1|+(Em*h/√2)*((Em*h/√2)/|Z3|)*Real(Z3)/|Z3| =(Em^2/2)*(Real(Z1)/|Z1|^2+h^2*Real(Z3)/|Z3|^2) =(Em^2/2)*((R/(1+(ωCR)^2))/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2*(R/(1+(3ωCR)^2))/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)) =(Em^2/2)*(R/(1+(ωCR)^2)*(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2*R/(1+(3ωCR)^2)*(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)) =(Em^2*R/2)*(1/(1+(ωCR)^2)*(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2/(1+(3ωCR)^2)*(R^2/(1+(ωCR)^2)^2+(3ω)^2/(L-CR^2/(1+(3ωCR)^2))^2)) ということになる。 著者の解では、基本波と高調波に対する合成インピーダンスの等価抵抗と等価リアクタンスをR1,X1,R3,X3と置いて R1=R/(1+(ωCR)^2) X1=ω(L-CR^2/(1+(ωCR)^2)) R3=R/(1+(3ωCR)^2) X3=3ω(L-CR^2/(1+(3ωCR)^2)) |I|=|IL|=(Em/√2)*sqrt(1/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)) =(Em/√2)/sqrt(1/(R1^2+X1^2)+h^2/(R3^2+X3^2)) |IR|=(Em/√2)*sqrt((1/(R^2/(1+(ωCR)^2)^2+ω^2/(L-CR^2/(1+(ωCR)^2))^2)*(1+(ωCR)^2)+h^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)*(1+(3ωCR)^2)) =(Em/√2)*sqrt(1/(R1^2+X1^2)*(1+(ωCR)^2)+h^2/(R3^2+X3^2)*(1+(3ωCR)^2)) |IC|=(Em/√2)*sqrt((ωCR)^2/(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)*(1+(ωCR)^2)+h^2*(3ωCR)^2/(R^2/(1+(3ωCR)^2)^2+(3ω)^2(L-CR^2/(1+(3ωCR)^2))^2)*(1+(3ωCR)^2)) =(Em/√2)*sqrt((ωCR)^2/(R1^2+X1^2)*(1+(ωCR)^2)+h^2*(3ωCR)^2/(R3^2+X3^2)*(1+(3ωCR)^2)) Pa=(Em^2*R/2)*(1/(1+(ωCR)^2)*(R^2/(1+(ωCR)^2)^2+ω^2(L-CR^2/(1+(ωCR)^2))^2)+h^2/(1+(3ωCR)^2)*(R^2/(1+(ωCR)^2)^2+(3ω)^2/(L-CR^2/(1+(3ωCR)^2))^2)) =(Em^2*R/2)*(1/(1+(ωCR)^2)*(R1^2+X1^2)+h^2/(1+(3ωCR)^2)*(R3^2+X3^2)) と簡略化している。 また著者はRとCに流れる電流を求める際に分流則を用いているが、すっかり分流則など忘れてしまったのでこちらの解では回路方程式から同じ結果を導きだしている。分流則を忘れてしまってもキルヒホッフの法則を憶えてさえいれば問題ない。 |
| webadm | 投稿日時: 2009-8-26 4:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【30】波形の同形性 次の問題はある意味奥が深い問題である。
以下のFourier級数展開で与えられた電圧と電流の波形が同形であるか確かめひずみ率を求めよというもの。 e=120*sin(ωt-60°)+60*cos(3ωt-180°)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) なんとなく題意の意味はわかるが、厳密に同形であることを調べるにはどうすればいいのかというのが難問である。 eとiの波形が同形であることを確認するには、eとiの波形の間に1対1の変換が存在することを証明する必要がある。 どうすんだこれ。 実は同形性の問題は奥が深く、信号処理で必ず習うナイキスト・シャノンの標本化定理はナイキストによって予測されていた連続時間系システムと離散時間系システムの同形性を数学的に証明したことに普遍的な意義がある。 デジタルコンピューターの登場と性能向上によって微分方程式の数値解法が開実用的になり、さまざまな物理演算やシミュレーションが連続時間系ではなく離散時間系の差分方程式の計算で行えるようになってきたが、反面現実の連続時間系システムとの同形性を確認しないまま数値だけを鵜呑みにしてしまう傾向が強くなっている。 離散時間系での差分方程式はさまざまな数学的な直交座標系では連続時間系の微分方程式と同形であることが知られているが、現実の世界の空間はさまざまな例外があって数学な空間とは異なることが多い。電磁界シミュレーターとかでは周囲を自由空間で囲まれていることを前提としているが、実際の機器はさまざまな導体や絶縁体で囲まれていたりする。ボールを投げるとボールが進む空間ではさまざまな方向の風にさらされる。恒星から発せられる光は太陽のそばでは巨大な重力によって歪んだ空間を直進し続けるが結果的に外から見ると曲がって進んでいるように見える。一見して予想と違ってみえる現実と理想との間にある未知の変換を施せば、互いの点と点は一対一の対応になるはずである。 信号処理ではこうした変換(標本化関数)がまだ数えるほどしか発見または考案されておらず、2次元や三次元などではほとんど未開拓であるだけに将来的に面白い分野である。 いずれ遠い将来に人間の知覚や認識、思考が連続時間系システムでどのように行われているか明らかになれば、それらはすぐに離散時間系システムで同形のことが可能なはずである。つまり人間の人格そのものをコンピューター内に移すこともいずれ可能になるだろう。 でなんの話だっけ? ああ、波形の同形性ね。 ちょっと熱が出てきたので休んでまた続きを。 前置きが長かったので式を再掲し整理してみると e=120*sin(ωt-60°)+60*cos(3ωt-180°)-30*sin(5ωt-140°) =120*sin(ωt-60°)-60*cos(3ωt)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) 2つの式を見比べると係数が6:1で位相が90°違っていることが定性的にわかる。 これをなんとか形式的に表すことができないだろうか、例えば変換マトリックスと逆変換マトリックスで。 例えばeとiを正方マトリックスで表すと e=([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) i=([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) ここでeからiへの変換マトリックスTが存在すると仮定すると T=([t11,t12,t13],[t21,t22,t23],[t31,t32,t33]) i=T.e Tに逆行列が存在するとすれば e=T^-1.i が成り立つようなTを見つければeとiは同形であると言える。 従って T=e^-1.i で表すことができる。 ここでeの逆行列は e^-1=([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)])^-1 =([1/(120*sin(ωt-60°)),0,0],[0,-1/(60*cos(3ωt)),0],[0,0,-1/(30*sin(5ωt-140°))]) これをiに乗じれば T=e^-1.i =([1/(120*sin(ωt-60°)),0,0],[0,-1/(60*cos(3ωt)),0],[0,0,-1/(30*sin(5ωt-140°))]).([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =([sin(ω+30°)/(6*sin(ωt-60°)),0,0],[0,sin(3ωt)/(6*cos(3ωt)),0],[0,0,sin(5ωt-50°)/(6*sin(5ωt-140°))]) ということになる。これには逆行列も存在し T^-1=([(6*sin(ω-60°))/sin(ωt+30°),0,0],[0,(6*cos(3ωt))/sin(3ωt),0],[0,0,(6*sin(5ωt-140°))/sin(5ωt-50°)]) ということになる。実際に検算してみると T.e=([sin(ω+30°)/(6*sin(ωt-60°)),0,0],[0,sin(3ωt)/(6*cos(3ωt)),0],[0,0,sin(5ωt-50°)/(6*sin(5ωt-140°))]).([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) =([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =i T^-1.i=([(6*sin(ω-60°))/sin(ωt+30°),0,0],[0,(6*cos(3ωt))/sin(3ωt),0],[0,0,(6*sin(5ωt-140°))/sin(5ωt-50°)]).([20*sin(ωt+30°),0,0],[0,-10*sin(3ωt),0],[0,0,-5*sin(5ωt-50°)]) =([120*sin(ωt-60°),0,0],[0,-60*cos(3ωt),0],[0,0,-30*sin(5ωt-140°)]) =e 当たり前だがそういうことになる。 従ってeとiは同型であると言える。 ひずみ率は基本波の実効値と高調波の実効値の比なので ひずみ率=sqrt(|E3|^2+|E5|^2)/|E1| =sqrt((60/√2)^2+(30/√2)^2)/(120/√2) =sqrt(60^2+30^2)/120 =sqrt(3600+900)/120 =sqrt(4500)/120 =10*3*sqrt(5)/120 =sqrt(5)/4 =0.56 同様に電流から求めると ひずみ率=sqrt(|I3|^2+|I5|^2)/|I1| =sqrt((10/√2)^2+(5/√2)^2)/(20/√2) =sqrt(10^2+5^2)/20 =sqrt(100+25)/20 =sqrt(125)/20 =5*sqrt(5)/20 =sqrt(5)/4 =0.56 ということになる。 P.S 同形と同型は異なる。 電圧の式を一部変えて e=100*sin(ωt-60°)-60*cos(3ωt)-30*sin(5ωt-140°) i=20*sin(ωt+30°)-10*sin(3ωt)-5*sin(5ωt-50°) とした場合、eとiは依然として同型であるが、ひずみ率を計算するとそれぞれ異なるので同形ではなくなる。 元の電圧の波形と一部Fourier係数を変えた電圧の波形をプロットしてみるほとんど見かけ上変わらない、同型であるゆえんである。 wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),-30*sin(5*x-(7*%pi)/9) +100*sin(x-%pi/3)-60*cos(3*x)], [x,-5,5])$ 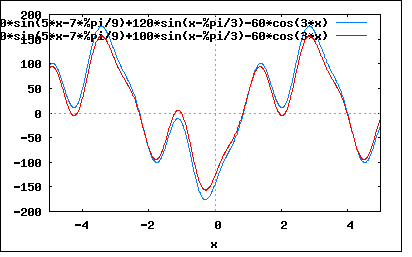 もともとの電圧と電流の波形をプロットして見比べてみると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),20*sin(x+2*%pi*30/360) -10*sin(3*x)-5*sin(5*x-2*%pi*50/360)], [x,-5,5])$ 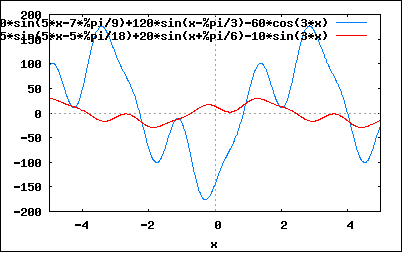 一見するとまるで似ても似つかない。 縦軸を対数表示にすると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),20*sin(x+2*%pi*30/360) -10*sin(3*x)-5*sin(5*x-2*%pi*50/360)], [x,-5,5], [gnuplot_preamble, "set logscale y; set grid;"])$ 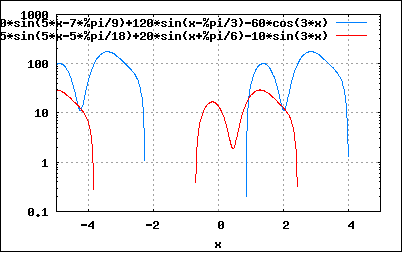 波形のレンジと位相が異なるものの同形の波形に見える。 一方同型だが同形ではない2つの電圧の波形を同様に対数圧縮してプロットすると wxplot2d([-30*sin(5*x-(7*%pi)/9)+120*sin(x-%pi/3)-60*cos(3*x),-30*sin(5*x-(7*%pi)/9) +100*sin(x-%pi/3)-60*cos(3*x)], [x,-5,5],[gnuplot_preamble, "set logscale y; set grid;"])$ 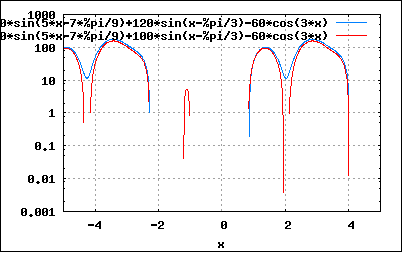 明らかに同じ波形ではないことが見てとれる。 人間の聴力とかは対数圧縮的な機能もっているので小さな音でも大きな音でも微妙にスペクトルが異なる音を聞き分けることができるのかもしれない。 音楽とか書物とかがソフトウェアなどですでにあるものの盗作であるかどうかを問題にするときにも同形性や同型性が問題になってくる。奥が深い問題である。 P.S この問題に真剣に組するとガロア理論に端を発する形式群論とか抽象数学の世界をマスターしないとどっかで行き倒れになりそうである。実際2次元以上の複素数やもっと高次元の同型性判定問題を扱うとなるとほとんど現代でも未踏の領域である。リーマンの生きた19世紀からほとんど進歩していないのだ。というのも難問すぎてみんなさじを投げてしまっているからだろう。グラフ理論なども一時期は盛り上がったが同形性問題に深い深い底なし沼があることがわかってから誰も寄り付かなくなった。恐ろしい世界である。 信号処理も最先端になると群論はむろんリーマン面とか先端数学を知らないとお友達になれない世界。 こんど群論に関しても古本を入手して学んでおくことにしよう。 P.S 2 よく考えれば、スペクトルが相似であれば波形は同形であると言えるのではないか。|I1'|,|I3'|,|I4'|が|I1|,|I3|,|I5|と以下の関係があるとすれば |I1'|=a|I1| |I3'|=a|I3| |I5'|=a|I5| とするとひずみ率は ひずみ率=sqrt(|I3'|^2+|I5'|^2)/|I1'| =sqrt((a|I3|)^2+(a|I5|)^2)/(a|I1|) =sqrt(|I3|^2+|I5|^2)/|I1| 従ってスペクトルが相似な元の波形と相似な波形ではひずみ率は同じになるということになり、すなわち同形であると言える。 一方上記の様にスペクトルが相似でない場合にはひずみ率は異なってしまうので同じ波形ではないということになる。 おそらく音声帯域であればスピーカーでならして耳で聞いてみればスペクトルが相似な同形の波形は同じ音色に聞こえ、そうでないものは異なる音色に聞こえることだろう。 |
| webadm | 投稿日時: 2009-8-26 2:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【29】全波整流波電圧の負荷電力 次の問題は前問の全波整流波電圧を抵抗に加えた場合に図の電圧計と電流計の指示から負荷電力を求めよというもの
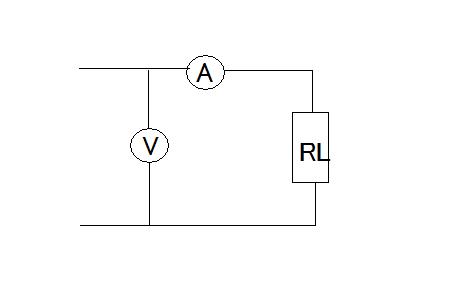 題意では以下の2つの計器について問われている。 (1)熱線型計器の場合 (2)可動コイル型計器の場合 いきなり計器の型が出てきたので困惑してしまう。 調べてみると熱線型とは、後に整流型とかTrue RMS型が現れる以前にあった原始的な交流メーターで、電流をいったん熱(I^2*R)に変換しそれによって熱伝対に発生する電圧から電流の実効値を表示するもの。しかし記憶ではFlukeから熱型と称するディジタルマルチメーターが出ていたと思うのだが、あれは本当に熱型なのだろうか、それともTrue RMSの別名なのだろうか? 一方可動コイル型は本来は直流電流を測るものだが、整流波を加えれば入力信号の平均値を示すことになる。 従って (1)の場合は、電圧および電流とも実効値なので消費電力は Pa=|E|*|I| =sqrt((1/T)∫e(t)^2dt)*sqrt((1/T)∫i(t)^2dt) (0≦t≦T) =sqrt((4/T)∫e(t)^2dt)*sqrt((4/T)∫i(t)^2dt) (0≦t≦T/4) =sqrt((4/T)∫(Em*sin(ωt))^2dt)*sqrt((4/T)∫(Im*sin(ωt))^2dt) =4*Em*Im*sqrt((1/T)∫sin(ωt)^2dt)*sqrt((1/T)∫sin(ωt)^2dt) =4*Em*Im*sqrt((1/T)∫(1/2-cos(2ωt)/2)dt)*sqrt((1/T)∫(1/2-cos(2ωt)/2)dt) =4*Em*Im*sqrt(1/8)*sqrt(1/8) =Em*Im/2 ということになる。 一方(2)の場合指示値は平均値なので電圧と電流の平均値は E=(1/T)∫e(t)dt (0≦t≦T) =(4/T)∫e(t)dt (0≦t≦T/4) =(4/T)∫Em*sin(ωt)dt =(4*Em/T)∫sin(ωt)dt =(4*Em/T)*(1/ω-cos(ωT/4)/ω) ここで ω=2π/T を代入すると E=(4*Em/T)*(1/(2π/T)-cos((2π/T)*T/4)/(2π/T)) =(2*Em/π)*(1-cos(π/2)) =2*Em/π I=(1/T)∫i(t)dt (0≦t≦T) =(4/T)∫i(t)dt (0≦t≦T/4) =(4/T)∫Im*sin(ωt)dt =(4*Im/T)∫sin(ωt)dt =(4*Im/T)*(1/ω-cos(ωT/4)/ω) ここで ω=2π/T を代入すると E=(4*Im/T)*(1/(2π/T)-cos((2π/T)*T/4)/(2π/T)) =(2*Im/π)*(1-cos(π/2)) =2*Im/π 平均値を使って電圧と電流の最大値を表すと Em=Eπ/2 Im=Iπ/2 従って消費電力は Pa=Em*Im/2 =(Eπ/2)*(Iπ/2)/2 =E*I*π^2/8 として導くことができる。 |
| webadm | 投稿日時: 2009-8-26 2:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【28】全波整流波電圧のFourier級数展開と波形率、波高率 次の問題は全波整流波電圧のFourier級数展開を求め、その波形率と波高率を求めよというもの。
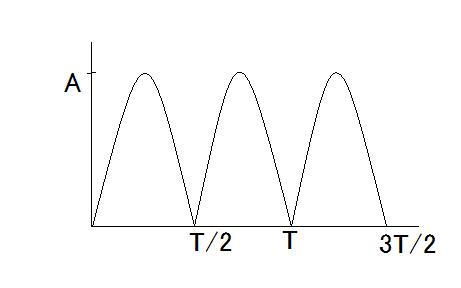 波形を式で表すと e(t)=A*sin(ωt) (0≦t≦T/2) =-A*sin(ωt) (T/2≦t≦T) この波形は遇関数波で、1/4周期毎に対称なのでそのFourier級数展開は e(t)=(1/2)b0+Σbn*cos(nωt) の形をとるはずである。従って b0=(4/T)∫e(t)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)dt =(4*A/T)∫sin(ωt)dt =(4*A/T)*(1/ω-cos(ωT/2)/ω) ここで ω=2π/T を代入すると b0=(4*A/T)*(1/(2π/T)-cos((2π/T)*T/2)/(2π/T)) =(2*A/π)*(1-cos(π)) =4*A/π また bn=(4/T)∫e(t)*cos(nωt)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)*cos(nωt)dt =(4*A/T)∫sin(ωt)*cos(nωt)dt =(4*A/T)*(-((n-1)*cos(((n+1)ωT)/2)+(-n-1)*cos(((n-1)ωT)/2))/((2*n^2-2)ω)-1/((n^2-1)ω) ここで ω=2π/T を代入すると bn=(4*A/T)*(((-cos(nπ)-1)*T)/(2πn^2-2π)) =-(2*A/π)*(cos(nπ)+1)/(n^2-1) =-(2*A/π)*((-1)^n+1)/(n^2-1) (n≠1) =-(4*A/π)/((2m)^2-1) (m=1,∞) ということになる。n=1の場合には別途求める必要がある b1=(4/T)∫e(t)*cos(ωt)dt (0≦t≦T/2) =(4/T)∫A*sin(ωt)*cos(ωt)dt =(4*A/T)∫sin(ωt)*cos(ωt)dt =(4*A/T)*(1/2ω-cos(ωT/2)^2/2ω) ここで ω=2π/T を代入すると b1=(4*A/T)*(1/2*(2π/T)-cos((2π/T)*T/2)^2/2*(2π/T)) =(A/π)*(1-cos(π)^2) =(A/π)*(1-(-1)^2) =0 ということになる。従ってFourier級数展開は e(t)=(1/2)*(4*A/π)+Σ(-(4*A/π)/((2m)^2-1))*cos((2m)ωt) (m=1,∞) =(4*A/π)*(1/2-(1/3)*cos(2ωt)-(1/15)*cos(4ωt)-(1/35)*cos(6ωt)-...) ということになる。 なんと整流前の基本波は含まれておらず、偶数次の高調波から成ることがわかる。 波形率は実効値と平均値の比なので 波形率=実効値/平均値 =sqrt((1/T)∫e(t)^2dt)/(1/T)∫e(t)dt (0≦t≦T) =sqrt((4/T)∫e(t)^2dt)/(4/T)∫e(t)dt (0≦t≦T/4) =sqrt((4/T)∫(A*sin(ωt))^2dt/(4/T)∫A*sin(ωt)dt =sqrt((4*A^2/T)∫(1/2-cos(2ωt)/2)dt/(4*A/T)∫sin(ωt)dt =2*A*sqrt((1/T)*(-(2*sin(ωT/2)-ωT)/8ω)/(4*A/T)*(-(cos(ωT/4)-1)/ω) ここで ω=2π/T を代入すると 波形率=2*A*sqrt((1/T)*(-(2*sin((2π/T)*T/2)-(2π/T)*T)/8*(2π/T))/(4*A/T)*(-(cos((2π/T)*T/4)-1)/(2π/T)) =2*A*sqrt(1/8)/(2*A)*(1/π) =π*sqrt(1/8) =π/2√2 ということになる。 また波高率は最大値と実効値の比なので 波高率=最大値/実効値 =A/2*A*sqrt(1/8) =1/2*sqrt(1/8) =1/2*(1/2√2) =√2 ということになる。 |
| « 1 2 3 4 (5) 6 7 8 » | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

