| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-8-22 20:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【17】キャパシタンスの補正係数(その2) 次ぎは同様に補正係数の計算問題。
前問で基本波の30%の第三高調波と20%の第五高調波をもつ電圧がキャパシタンスCのみの回路に加えられた時のキャパシタンスCの見かけ上どうなるかを示せというもの。 そこで E1=E, E3=0.3*E, E5=0.2*E とした場合のCを前問の式で求めてみると C=(|I|/ω*|E|)*sqrt((E1^2+E3^2+E5^2)/(E1^2+9*E3^2+25*E5^2)) =(|I|/ω*|E|)*sqrt((E^2+(0.3*E)^2+(0.2*E)^2)/(E^2+9*(0.3*E)^2+25*(0.2*E)^2)) =(|I|/ω*|E|)*sqrt((1+0.3^2+0.2^2)/(1+9*0.3^2+25*0.2^2)) =(|I|/ω*|E|)*sqrt((1+0.09+0.04)/(1+9*0.09+25*0.04)) =(|I|/ω*|E|)*sqrt(1.13/(1+0.81+1)) =(|I|/ω*|E|)*sqrt(1.13/2.81) =(|I|/ω*|E|)*0.634 従って見かけ上のキャパシタンスに対して実際のCは46.6%低いことになる。 逆に見かけ上のキャパシタンスをC'とすると C'=C/0.63 =1.577*C 見かけ上のキャパシタンスは実際のCより57.7%大きく見えることになる。 |
| webadm | 投稿日時: 2009-8-22 20:09 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【16】キャパシタンスの補正係数 次ぎの問題は前問と似たようなキャパシタンスの補正係数に関するもの。
以下の電圧がキャパシタンスCに加えられる時にその電圧と電流の実効値を求め、それを用いてキャパシタンスCを表せというもの。 e=ΣEn*sin(nωt+θn) まず電圧の実効値は |E|=sqrt((1/T)∫e^2dt) =sqrt((1/T)∫(ΣEn*sin(nωt+θn))dt) =sqrt((1/T)∫(E1*sin(ωt+θ1)+E2*sin(2ωt+θ2)+...+En*sin(nωt+θn))dt) =sqrt((1/T)∫(E1^2*sin(ωt+θ1)^2+E2^2*sin(2ωt+θ2)^2+...+En^2*sin(nωt+θn)^2+E1*sin(ωt+θ1)*(E2*sin(2ωt+θ2)+...+En*sin(nωt+θn))+E2*sin(2ωt+θ2)*(E1*sin(ωt+θ1)+E3*sin(3ωt+θ3)+...+En*sin(nωt+θn))+...)dt) =sqrt((1/T)*(E1^2∫sin(ωt+θ1)^2dt+E2^2∫sin(2ωt+θ2)^2dt+...+En^2∫sin(nωt+θn)^2dt)) =sqrt((1/T)*(E1^2∫(1/2-cos(2ωt+2θ1)/2)dt+E2^2∫(1/2-cos(4ωt+2θ2)/2)dt+...+En^2∫(1/2-cos(2nωt+2θn)/2)dt)) =sqrt(E1^2/2+E2^2/2+...+En^2/2) =(1/√2)*sqrt(E1^2+E2^2+...+En^2) ということになる。 Cに流れる電流の瞬時値は i=C*de/dt =C*d(ΣEn*sin(nωt+θn))/dt =C*d(E1*sin(ωt+θ1)+E2*sin(2ωt+θ2)+...+En*sin(nωt+θn))/dt =C*(E1*ω*cos(ωt+θ1)+E2*2ω*cos(2ωt+θ2)+...+En*nω*cos(nωt+θn)) =ωC*(E1*cos(ωt+θ1)+2*E2*cos(2ωt+θ2)+...+n*En*cos(nωt+θn)) 従って実効値は |I|=sqrt((1/T)∫i^2dt) =sqrt((1/T)∫ωC*(E1*cos(ωt+θ1)+2*E2*cos(2ωt+θ2)+...+n*En*cos(nωt+θn)))^2dt) =ωC*sqrt((1/T)∫(E1^2*cos(ωt+θ1)^2+4*E2^2*cos(2ωt+θ2)^2+...+n^2*En^2*cos(nωt+θn)^2+E1*cos(ωt+θ1)*(E2*cos(2ωt+θ2)+...+En*cos(nωt+θn)+E2*cos(2ωt+θ2)*(E1*cos(ωt+θ1)+E3*cos(3ωt+θ3)+...+En*cos(nωt+θn))+...)dt) =ωC*sqrt((1/T)*(E1^2∫cos(ωt+θ1)^2dt+4*E2^2∫cos(2ωt+θ2)^2dt+...+n^2*En^2∫cos(nωt+θn)^2dt)) =ωC*sqrt((1/T)*(E1^2∫(1/2+sin(2ωt+2θ1)/2)dt+4*E2^2∫(1/2+sin(4ωt+2θ)/2)dt+...+n^2*En^2∫(1/2+sin(2nωt+2θ2)/2)dt) =ωC*sqrt((E1^2/2+4*E2^2/2+...+n^2*En^2/2) =(ωC/√2)*sqrt(E1^2+4*E2^2+...+n^2*En^2) ということになる。従ってCについて解くと C=√2*|I|/(ω*sqrt(E1^2+4*E2^2+...+n^2*En^2)) 分母と分子に電圧の実効値の式の左辺と右辺をそれぞれ乗じると C=√2*|I|*(1/√2)*sqrt(E1^2+E2^2+...+En^2)/(ω*|E|*sqrt(E1^2+4*E2^2+...+n^2*En^2)) =(|I|/ω*|E|)*sqrt((E1^2+E2^2+...+En^2)/(E1^2+4*E2^2+...+n^2*En^2)) ということになる。ここで(|I|/ω*|E|)が電圧と電流の実効値と等価正弦波の各周波数から計算される見かけ上のキャパシタンスで残りがキャパシタンスの補正係数である。 著者の解は依然として基本波と高調波の実効値の記号と瞬時値の最大値の記号に同じEnを用いていて紛らわしい。本来は e=ΣEmn*sin(nωt+θn) として |En|=Emn/√2 とすべきところだろう。 |
| webadm | 投稿日時: 2009-8-22 12:02 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【15】インダクタンスの補正係数 次ぎの問題は前問に関連するもので、基本波の30%の第二高調波と20%の第三高調波をもつ電圧がインダクタンスに加えられたときのインダクタンスの補正係数を求めよというもの。
電圧を式にすると e=E1*sin(ωt)+(0.3*E1)*sin(2ωt)+(0.2*E1)*sin(3ωt) ということになる。 電圧の実効値は |E|=sqrt((1/T)∫e^2dt) =sqrt((1/T)∫(E1*sin(ωt)+(0.3*E1)*sin(2ωt)+(0.2*E1)*sin(3ωt))^2dt) =sqrt((1/T)∫(E1^2*sin(ωt)^2+(0.3*E1)^2*sin(2ωt)^2+(0.2*E1)^2*sin(3ωt)^2+E1*sin(ωt)*((0.3*E1)*sin(2ωt)+(0.2*E1)*sin(3ωt))+(0.3*E1)*sin(2ωt)*(E1*sin(ωt)+(0.2*E1)*sin(3ωt))+(0.2*E1)*sin(3ωt)*(E1*sin(ωt)+(0.3*E1)*sin(2ωt)))dt) =sqrt((1/T)*(E1^2∫sin(ωt)^2dt+(0.3*E1)^2∫sin(2ωt)^2dt+(0.2*E1)^2∫sin(3ωt)^2dt) =sqrt((1/T)*(E1^2∫(1/2-cos(2ωt)/2)dt+(0.3*E1)^2∫(1/2-cos(4ωt)/2)dt+(0.2*E1)^2∫(1/2-cos(6ωt)/2)dt)) =sqrt(E1^2/2+(0.3*E1)^2/2+(0.2*E1)^2/2) =(1/√2)*sqrt(E1^2+(0.3*E1)^2+(0.2*E1)^2) =(E1/√2)*sqrt(1+0.3^2+0.2^2) 電流の瞬時値は i=(1/L)∫edt =(1/L)∫(E1*sin(ωt)+(0.3*E1)*sin(2ωt)+(0.2*E1)*sin(3ωt))dt =(1/L)*(E1∫sin(ωt)dt+(0.3*E1)∫sin(2ωt)dt+(0.2*E1)∫sin(3ωt)dt) =(1/L)*(E1*(-cos(ωt)/ω)+(0.3*E1)*(-cos(2ωt)/2ω)+(0.2*E1)*(-cos(3ωt)/3ω)) =-(1/ωL)*(E1*cos(ωt)+(0.3*E1)*cos(2ωt)/2+(0.2*E1)*cos(3ωt)/3) 電流の実効値は |I|=sqrt((1/T)∫i^2dt) =sqrt((1/T)∫(-(1/ωL)*(E1*cos(ωt)+(0.3*E1)*cos(2ωt)/2+(0.2*E1)*cos(3ωt)/3))^2dt) =(1/ωL)*sqrt((1/T)∫(E1^2*cos(ωt)^2+(0.3*E1)^2*cos(2ωt)^2/4+(0.2*E1)^2*cos(3ωt)^2/9+E1*cos(ωt)*((0.3*E1)*cos(2ωt)/2+(0.2*E1)*cos(3ωt)/3)+(0.3*E1/2)*cos(2ωt)*(E1*cos(ωt)+(0.2*E1)*cos(3ωt)/3)+(0.2*E1/3)*cos(3ωt)*(E1*cos(ωt)+(0.3*E1)*cos(2ωt)/2))dt) =(1/ωL)*sqrt((1/T)*(E1^2∫cos(ωt)^2dt+(0.3*E1/2)^2∫cos(2ωt)^2dt+(0.2*E1/3)^2∫cos(3ωt)^2dt)) =(1/ωL)*sqrt((1/T)*(E1^2∫(1/2+sin(2ωt)/2)dt+(0.3*E1/2)^2∫(1/2+sin(4ωt)/2)dt+(0.2*E1/3)^2∫(1/2+sin(6ωt)/2)dt)) =(1/ωL)*sqrt(E1^2/2+(0.3*E1/2)^2/2+(0.2*E1/3)^2/2) =(1/√2ωL)*sqrt(E1^2+(0.3*E1)^2/4+(0.2*E1)^2/9) =(E1/√2ωL)*sqrt(1+0.3^2/4+0.2^2/9) 従ってLは L=(E1/√2ω|I|)*sqrt(1+0.3^2/4+0.2^2/9) 分子と分母に電圧の実効値の式の左辺と右辺をそれぞれ乗じると L=(E1*|E|/√2ω|I|)*sqrt(1+0.3^2/4+0.2^2/9)/((E1/√2)*sqrt(1+0.3^2+0.2^2)) =(|E|/ω|I|)*sqrt((1+0.3^2/4+0.2^2/9)/(1+0.3^2+0.2^2)) =(|E|/ω|I|)*sqrt((1+0.09/4+0.04/9)/(1+0.09+0.04)) =(|E|/ω|I|)*sqrt((1+0.0225+0.00444)/1.13) =(|E|/ω|I|)*sqrt(1.027/1.13) =(|E|/ω|I|)*0.953 ということになる。これは|E|/ω|I|で計算される見かけのインダクタンスよりも実際のインダクタンスは4.7%低いことを意味する。誤解を招かないようにすると、高調波になればなるほど電流が流れ難くなるので等価正弦波としての電圧実効値|E|と各周波数ωそれに電流実効値|I|から逆算した見かけ上のインダクタンスは実際のLよりも大きな値となるという意味である。 見かけ上のインダクタンスをL'とすると L'=L/0.953 =1.049*L 従って実際のLよりも4.9%大きいように見えるということになる。 公式を丸暗記していれば何もいちいち瞬時値を二乗平均して実効値を導かなくても良いわけだが、いかんせんIQが低いのですぐ忘れてしまう。これだけ同じことを繰り返せばいい加減暗記してしまうかもしれない。大抵6回繰り返しやれば憶えてしまうものだ。 |
| webadm | 投稿日時: 2009-8-22 11:14 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【14】ひずみ波の実効値 次ぎも実効値に関する問題。
e=ΣEn*sin(nωt+θn) で与えられる電圧がインダクタンスLに加えられた時にその電圧と電流の実効値を求めよというもの。またLを電圧と電流の実効値で表せというもの。 これもひずみ波の実効値の公式を忘れてしまっても、線形回路網の重ね合わせの理と正弦波交流の実効値と忘れなければ導くことができる。 最初にLに加わる電圧の実効値は |E|=sqrt((1/T)∫e^2dt) =sqrt((1/T)∫(ΣEn*sin(nωt+θn))^2dt) =sqrt((1/T)∫(E1*sin(ωt+θ1)+E2*sin(2ωt+θ2)+E3*sin(3ωt+θ3)+...+En*sin(nωt+θn))^2dt) =sqrt((1/T)∫(E1^2*sin(ωt+θ1)^2+E2^2*sin(2ωt+θ2)^2+E3^2*sin(3ωt+θ3)^2+En^2*sin(nωt+θn)^2+E1*sin(ωt+θ1)*(E2*sin(2ωt+θ2)+E3*sin(3ωt+θ3)+...+En*sin(nωt+θn)+E2*sin(2ωt+θ2)*(E1*sin(ωt+θ1)+E3*sin(3ωt+θ3)+...+En*sin(nωt+θn))+...)dt) =sqrt((1/T)*(E1^2∫sin(ωt+θ1)^2dt+E2^2∫sin(2ωt+θ2)^2dt+E3^2∫sin(3ωt+θ3)^2dt)) =sqrt((1/T)*(E1^2∫(1/2-cos(2ωt+2θ1)/2)dt+E2^2∫(1/2-cos(4ωt+2θ2)/2)dt+E3^2∫(1/2-cos(6ωt+2θ3)/2)dt)) =sqrt(E1^2/2+E2^2/2+E3^2/2+...+En^2/2) =(1/√2)*sqrt(E1^2+E2^2+E3^2+...+En^2) ということになる。 一方Lに流れる電流の瞬時値は I=(1/L)∫edt =(1/L)∫ΣEn*sin(nωt+θn)dt =(1/L)∫(E1*sin(ωt+θ1)+E2*sin(2ωt+θ2)+E3*sin(3ωt+θ3)+...+En*sin(nωt+θn))dt =(1/L)*(E1∫sin(ωt+θ1)dt+E2∫sin(2ωt+θ2)dt+E3∫sin(3ωt+θ3)dt+...+En∫sin(nωt+θn)dt) =(1/L)*(E1*(-cos(ωt+θ1)/ω)+E2*(-cos(2ωt+θ2)/2ω)+E3*(-cos(3ωt+θ3)/3ω)+...+En*(-cos(nωt+θn)/nω)) =-(1/ωL)*(E1*cos(ωt+θ1)+E2*cos(2ωt+θ2)/2+E3*cos(3ωt+θ3)/3+...+En*cos(nωt+θn)/n) ということになる。従ってLを流れる電流の実効値は |I|=sqrt((1/T)∫I^2dt) =sqrt((1/T)∫(-(1/ωL)*(E1*cos(ωt+θ1)+E2*cos(2ωt+θ2)/2+E3*cos(3ωt+θ3)/3+...+En*cos(nωt+θn)/n))^2dt) =(1/ωL)*sqrt((1/T)∫(E1^2*cos(ωt+θ1)^2+E2^2*cos(2ωt+θ2)^2/4+E3^2*cos(3ωt+θ3)^2/9+...+En^2*cos(nωt+θn)^2/n^2+E1*cos(ωt+θ1)*(E2*cos(2ωt+θ2)/2+E3*cos(3ωt+θ3)/3+...+En*cos(nωt+θn)/n)+E2*cos(2ωt+θ2)*(E1*cos(ωt+θ1)+E3*cos(3ωt+θ3)+...+En*cos(nωt+θn)+...)dt) =(1/ωL)*sqrt((1/T)*(E1^2∫cos(ωt+θ1)^2dt+(E2^2/4)∫cos(2ωt+θ2)^2dt+(E3^2/9)∫cos(3ωt+θ3)dt)) =(1/ωL)*sqrt((1/T)*(E1^2∫(1/2+sin(2ωt+2θ1)/2)dt+(E2^2/4)∫(1/2+sin(4ωt+2θ2)/2)dt+(E3^2/9)∫(1/2+sin(6ωt+2θ3)/2)dt+...+(En^2/n^2)∫(1/2+sin(2nωt+2θn)/2)dt)) =(1/ωL)*sqrt(E1^2/2+(E2^2/8)+(E3^2/18)+...+(En^2/2n^2)) =(1/√2ωL)*sqrt(E1^2+(E2^2/4)+(E3^2/9)+...+(En^2/n^2)) ということになる。 従ってLは上の式より L=(1/√2ω|I|)*sqrt(E1^2+(E2^2/4)+(E3^2/9)+...+(En^2/n^2)) 分子と分母にそれぞれ電圧の実効値の左辺と右辺を乗ずると L=(|E|/√2ω|I|)*sqrt(E1^2+(E^2/4)+(E3^2/9)+...+(En^2/n^2))/(1/√2)*sqrt(E1^2+E2^2+E3^2+...+En^2) =(|E|/ω|I|)*sqrt((E1^2+(E2^2/4)+(E3^2/9)+...+(En^2/n^2))/(E1^2+E2^2+E3^3+...+En^2)) ということになる。 ここで|E|/ω|I|は実効値から計算される見かけ上のインダクタンスとすると残りの係数はインダクタンスの補正係数と呼ぶ。 著者はひずみ波の実効値の公式をそのまま持ってきているが、基本波それに高調波の実効値の記号とひずみ波の基本波それに高調波の振幅の記号に同じEnを用いているので誤解を招く。本来は |E|=sqrt(|E1|^2+|E2|^2+|E3|^2+...+|En|^2) ただし |En|=En/√2 とすべきところだろう。これでもまだ紛らわしいのだが。 もしくは最初から振幅と実効値の記号を分けて。 e=ΣEmn*sin(nωt+θn) として |En|=Emn/√2 とでもするべきだろう。 |
| webadm | 投稿日時: 2009-8-22 7:06 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【13】ひずみ波の電流 次ぎの問題は図にあるようなひずみ波の電源をLC並列回路につないだ場合に流れる電流を求めよというもの。
理論の時に導いたはずのひずみ波の実効電流の公式などすっかり忘れてしまっているので、おさらいしてみよう。 基本的にひずみ波の回路解析は重ね合わせの理を使用する。 題意では以下の起電力を持つ電源 e(t)=E1*sin(ωt)+E3*sin(3ωt+θ) をLC並列回路につないだ場合に、流れる電流を求めよというもの。 異なる周波数の交流電源が直列につながっていると考えればそれぞれの電源だけがつながった回路を重ね合わせればよいことになる。 基本波のみの場合に流れる電流の瞬時値は e1=E1*sin(ωt) i1L=∫(e1/L)dt =∫(E1*sin(ωt)/L)dt =(E1/L)∫sin(ωt)dt =(E1/L)*(-cos(ωt)/ω) =-E1*cos(ωt)/ωL i1C=C*de/dt =C*d(E1*sin(ωt))/dt =ωC*E1*cos(ωt) 従って基本波のみの場合に全体を流れる電流は i1=i1L+i2C =E1*cos(ωt)*(ωC-1/ωL) 一方第三高調波のみで流れる電流の瞬時値は e3=E3*sin(3ωt+θ) i3L=∫(e3/L)dt =∫(E3*sin(3ωt+θ)/L)dt =(E3/L)∫sin(3ωt+θ)dt =(E3/L)*(-cos(3ωt+θ)/3ω) =-E3*cos(3ωt+θ)/3ωL i3C=C*de/dt =C*d(E3*sin(3ωt+θ)/dt =C*E3*d(sin(3ωt+θ)dt =C*E3*(3ω*cos(3ωt+θ) =3ωC*E3*cos(3ωt+θ) 従ってLとCを流れる電流の瞬時値はそれぞれ iL=i1L+i3L =-E1*cos(ωt)/ωL-E3*cos(3ωt+θ)/3ωL =-(E1*cos(ωt)/ωL+E3*cos(3ωt+θ)/3ωL) iC=i1C+i3C =ωC*E1*cos(ωt)+3ωC*E3*cos(3ωt+θ) =ωC*(E1*cos(ωt)+3*E3*cos(3ωt+θ)) 従ってLとCを流れるそれぞれの電流の実効値は |iL|=sqrt((1/T)∫iL^2dt) =sqrt((1/T)∫(-(E1*cos(ωt)/ωL+E3*cos(3ωt+θ)/3ωL))^2dt) =sqrt((1/T)∫(E1^2*cos(ωt)^2/ω^2L^2+E3^2*cos(3ωt+θ)^2/9ω^2L^2+2*E1*E3*cos(ωt)*cos(3ωt+θ)/3ω^2L^2)dt) =sqrt((1/T)*((E1^2/ω^2L^2)∫cos(ωt)^2dt+(E3^2/9ω^2L^2)∫cos(3ωt+θ)^2dt+(2*E1*E3/3ω^2L^2)∫cos(ωt)*cos(3ωt+θ)dt)) =sqrt((1/T)*((E1^2/ω^2L^2)∫(cos(0)/2+cos(2ωt)/2)dt+(E3^2/9ω^2L^2)∫(cos(0)/2+cos(6ωt+2θ)/2)dt+(2*E1*E3/3ω^2L^2)∫(cos(-2ωt-θ)/2+cos(4ωt+θ)/2)dt)) =sqrt((1/T)*((E1^2/ω^2L^2)∫(1/2+cos(2ωt)/2)dt+(E3^2/9ω^2L^2)∫(1/2+cos(6ωt+θ)/2)dt+(2*E1*E3/3ω^2L^2)∫(cos(2ωt+θ)/2+cos(4ωt+θ)/2)dt)) =sqrt(E1^2/2ω^2L^2+E3^2/18ω^2L^2) =(1/√2)*sqrt(E1^2/ω^2L^2+E3^2/9ω^2L^2) =(1/√2ωL)*sqrt(E1^2+E3^2/9) |iC|=sqrt((1/T)∫iC^2dt) =sqrt((1/T)∫(ωC*(E1*cos(ωt)+3*E3*cos(3ωt+θ)))^2dt) =sqrt((1/T)∫(ω^2C^2*(E1^2*cos(ωt)^2+9*E3^2*cos(3ωt+θ)^2+6*E1*E3*cos(ωt)*cos(3ωt+θ))dt) =ωC*sqrt((1/T)*(E1^2∫cos(ωt)^2dt+9*E3^2∫cos(3ωt+θ)^2dt+6*E1*E3∫cos(ωt)*cos(3ωt+θ)dt)) =ωC*sqrt((1/T)*(E1^2∫(cos(0)/2+cos(2ωt)/2)dt+9*E3^2∫(cos(0)/2+cos(6ωt+2θ)/2)dt+6*E1*E3∫(cos(-2ωt-θ)/2+cos(4ωt+θ)/2)dt)) =ωC*sqrt((1/T)*(E1^2∫(1/2+cos(2ωt)/2)dt+9*E3^2∫(1/2+cos(6ωt+2θ)/2)dt+6*E1*E3∫(cos(2ωt+θ)/2+cos(4ωt+θ)/2)dt)) =ωC*sqrt(E1^2/2+9*E3^2/2) =(ωC/√2)*sqrt(E1^2+9*E3^2) ということになる。 また第三高調波のみで全体を流れる電流は i3=i3L+i3C =-E3*cos(3ωt+θ)/3ωL+3ωC*E3*cos(3ωt+θ) =E3*cos(3ωt+θ)*(3ωC-1/3ωL) 従って全体を流れる電流の瞬時値は上記の重ね合わせで i=i1+i3 =E1*cos(ωt)*(ωC-1/ωL)+E3*cos(3ωt+θ)*(3ωC-1/3ωL) ということになる。 全体を流れる電流の実効値は |i|=sqrt((1/T)∫i^2dt) =sqrt((1/T)∫(E1*cos(ωt)*(ωC-1/ωL)+E3*cos(3ωt+θ)*(3ωC-1/3ωL))^2dt) =sqrt((1/T)∫(E1^2*cos(ωt)^2*(ωC-1/ωL)^2+E3^3*cos(3ωt+θ)^2*(3ωC-1/3ωL)^2+2*E1*cos(ωt)*(ωC-1/ωL)*E3*cos(3ωt+θ)*(3ωC-1/3ωL))dt) =sqrt((1/T)*(E1^2*(ωC-1/ωL)^2∫cos(ωt)^2dt+E3^2*(3ωC-1/3ωL)^2∫cos(3ωt+θ)^2dt+2*E1*E3*(ωC-1/ωL)*(3ωC-1/3ωL)∫cos(ωt)*cos(3ωt+θ)dt)) =sqrt((1/T)*(E1^2*(ωC-1/ωL)^2∫(cos(0)/2+cos(2ωt)/2)dt+E3^2*(3ωC-1/3ωL)^2∫(cos(0)/2+cos(6ωt+2θ)/2)dt+2*E1*E3*(ωC-1/ωL)*(3ωC-1/3ωL)∫(cos(-2ωt-θ)/2+cos(4ωt+θ)/2)dt)) =sqrt((1/T)*(E1^2*(ωC-1/ωL)^2∫(1/2+cos(2ωt)/2)dt+E3^2*(3ωC-1/3ωL)^2∫(1/2+cos(6ωt+2θ)/2)dt+2*E1*E3*(ωC-1/ωL)*(3ωC-1/3ωL)*∫(cos(2ωt+θ)/2+cos(4ωt+θ)/2)dt)) =sqrt(E1^2*(ωC-1/ωL)^2/2+E3^2*(3ωC-1/3ωL)^2/2) =(1/√2)*sqrt(E1^2*(ωC-1/ωL)^2+E3^2*(3ωC-1/3ωL)^2) ということになる。 間違いを犯し易いのはLとCに流れる電流の実効値の合計が全体を流れる電流の実効値と考えてしまいがちな点。実効値は定義上あくまで瞬時値から二乗平均として求めなければならない。重ね合わせの理が有効なのは瞬時値だけである。 著者の解では最初に個々の電源単独での電流の実効値を求めたものの、それをひずみ波の実効値の式に適用すると誤った解になってしまうのに気づいて、途中でLとCを流れる電流は位相が180°異なるというもっともらしい理由から別の電流の実効値の式を持ち出してきてそれに基づいてひずみ波の実効値の公式にあてはめて最終的な結果を得ている。いささか結論が先にあって、それに合うような個々の電源に関する電流実効値の式をでっち上げたとも見える。 それに第三高調波の電圧の式に誤記がある。本来は e3=E3*sin(3ωt+θ) とあるべきところが e3=E3*sin(ωt+θ) となっている。 |
| webadm | 投稿日時: 2009-8-21 10:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【12】ノコギリ波のFourier級数展開(その4) 次ぎは再びノコギリ波のFourier級数展開の応用問題。
以前の問題で出てきたノコギリ波をちょうどすべての値が正になるように直流バイアスを加えたような波形。 これをFourier級数展開するのは単純であるが、それだと著者の解と変わりばえしないので、へそ曲がりな方法でやってみよう。 前にもやった重ね合わせを使った方法でいく。 この波形は以前の問題に出てきた奇関数波のノコギリ波の振幅を半分にし、位相をT/2進めたものに正の直流バイアスを重ねたものと等しい。すなわち f(t)=Σ(2*A/π)*((-1)^n+1/n)*sin(nωt) =(2*A/π)*(sin(ωt)-(1/2)*sin(2ωt)+(1/3)*sin(3ωt)-...) これに対して直流バイアス信号 g(t)=A/2 を重ね合わせると y(t)=(1/2)*f(t+T/2)+g(t) =(1/2)*(2*A/π)*(sin(ω(t+T/2)-(1/2)*sin(2ω(t+T/2))+(1/3)*sin(3ω(t+T/2)-...)+A/2 =(A/π)*(sin(ω(t+T/2))-(1/2)*sin(2ω(t+T))+(1/3)*sin(3ω(t+T/2)-...)+A/2 ここで T=2π/ω を代入すると y(t)=(A/π)*(sin(ωt+π)-(1/2)*sin(2ωt+2π)+(1/3)*sin(3ωt+3π)-...)+A/2 =(A/π)*(-sin(ωt)-(1/2)*sin(2ωt)-(1/3)*sin(3ωt)-...)+A/2 =A/2-(A/π)*(sin(ωt)+(1/2)*sin(2ωt)+(1/3)*sin(3ωt)+...) ということになる。 なんだ簡単じゃないか。 もう一つの題意として、実効値をFourier係数から求めたものと波形から求めたものを比較してみろというものがある。 Fourier係数から実効値を求めるには、電源の重ね合わせと同じなので周波数領域から求めた実効値という意味で|y|ωとすると |y|ω=sqrt((A/2)^2+Σ((-A/nπ)/√2)^2) =sqrt(A^2/4+(A^2/2π^2)Σ(1/n^2)) ここで無限級数展開の公式より Σ(1/n^2)=π^2/6 なので |y|ω=sqrt(A^2/4+(A^2/2π^2)*(π^2/6)) =sqrt(A^2/4+A^2/12) =sqrt(3*A^2/12+A^2/12) =sqrt(4*A^2/12) =sqrt(A^2/3) =A/√3 ということになる。 一方時間領域から実効値を求めると |y|t=sqrt((1/T)∫y(t)^2dt) =sqrt((1/T)∫(A*t/T)^2*dt) =sqrt((1/T)*(A^2/T^2)∫t^2dt) =sqrt((1/T)*(A^2/T^2)*(T^3/3)) =sqrt(A^2/3) =A/√3 ということになり、周波数領域から求めた実効値と時間領域から求めた実効値は一致する。 これはFFTアナライザーなどで入力信号の実効値を周波数領域のスペクトルから求めるのにも使用されている。 P.S 本方法の嵌りどころはf(t)とg(t)の重ね合わせの際にf(t)の位相をずらすことにある。f(t)+g(t)でも時間軸上の繰り返し波形は同じだが位相が異なりスペクトルの極性が変わってしまう。 y(t)=f(t)+g(t) =A/2+(A/π)*(sin(ωt)-(1/2)*sin(2ωt)+(1/3)*sin(3ωt)-...) これをプロットしてみると wxplot2d([(sin(3*x)/3-sin(2*x)/2+sin(x))/%pi+1/2], [x,0,4*%pi])$ 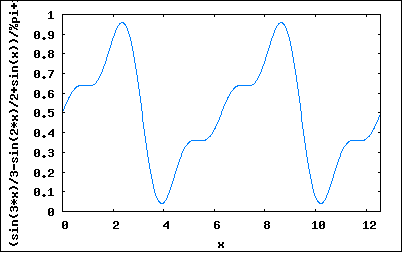 位相がずれているだけ。 一方位相を予めT/2進めたものは wxplot2d([(-sin(3*x)/3-sin(2*x)/2-sin(x))/%pi+1/2], [x,0,4*%pi])$ 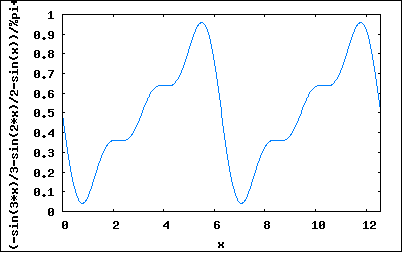 三次の高調波までなので収束が甘いが、題意のノコギリ波に近づいていることは確か。 異なるのはFourier係数の符合だけで絶対値は同じである。位相に関する情報がFourier係数の符合に現れていることになる。一般のFFTやスペクトルアナライザで表示するとどちらも同じ線スペクトルを表示することになる(RMS表示であるため)。反面位相に関する情報は失われる。 他の解法としては、以前の問題で最初に出てきたノコギリ波のデューティ比を100%にしたものとしてFourier級数展開を求めることができる。この場合は任意のデューティ比のノコギリ波のFourier級数展開を求めてディーティ比を100%と置く事になるので面倒くさい。しかしながらディーティ比を買えた場合に周波数領域のスペクトルがどのように変化するのか解析することができる。 |
| webadm | 投稿日時: 2009-8-20 8:03 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【11】台形波のFourier級数展開 次ぎもFourier級数展開の問題。以下の様な台形波をFourier級数展開する。
波形は明らかに奇関数波なので奇関数の基本波と高調波のみでFourier級数展開されることは想像に難くない。 それだと著者の解と同じなので面白くないので、別の方法でやってみよう。 以前の問題でもやった重ね合わせの理で求めてみよう。 問題の台形波はデューティ比50%の矩形波に以下のノコギリ波を重ね合わせたものと考えることが出来る。 この波形も奇関数波でかつ対称波である。 最初に矩形波のFourier級数展開を導くと奇関数波でかつ対称波なので奇数次の高調波からなり b0=bn=0 従って an=(4/T)∫f(t)*sin((2m+1)ωt)dt (0≦t≦T/2) =(8/T)∫f(t)*sin((2m+1)ωt)dt (0≦t≦T/4) =(8/T)∫A*sin((2m+1)ωt)dt (m=0,∞) =(8*A/T)∫sin((2m+1)ωt)dt (0≦t≦T/4) =(8*A/T)*(1/(2m+1)ω-cos((2m+1)ωT/4)/(2m+1)ω) ここで ω=2π/T を代入すると an=(8*A/T)*(T/2π(2m+1)-Tcos((2m+1)π/2)/2π(2m+1)) =4*A/(2m+1)π 従って矩形波のFourier級数展開は f(t)=(4*A/π)Σ(sin((2m+1)ωt)/(2m+1)) =(4*A/π)*(sin(ωt)+sin(3ωt)/3+sin(5ωt)/5+...) ということになる。プロットしてみると、 wxplot2d([(4*(sin(5*x)/5+sin(3*x)/3+sin(x)))/%pi], [x,-5,5])$ 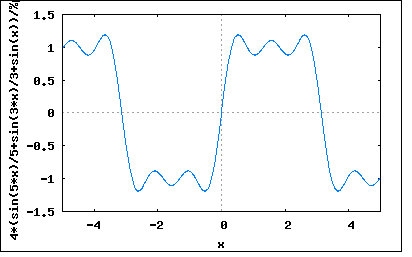 一方重ね合わせるノコギリ波のFourier級数展開も奇関数波でかつ対称波なので g(t)=-(A/τ)*(τ-t) =-f(τ-t) (0≦t≦τ) =0 (τ≦t≦T/4) 従ってFourier係数は an=(8/T)∫g(t)*sin((2m+1)ωt)dt (0≦t≦T/4) =(8/T)∫(-A/τ)*(τ-t)*sin((2m+1)ωt)dt (0≦t≦τ) =-(8*A/Tτ)∫(τ-t)*sin((2m+1)ωt)dt =-(8*A/Tτ)*(τ/(2m+1)ω-sin((2m+1)ωτ)/(2m+1)^2*ω^2) ここで T=2π/ω を代入すると an=-(4*A/πτ)*(τ/(2m+1)-sin((2m+1)ωτ)/(2m+1)^2*ω) =-4*A/(2m+1)π+(4*A/(2m+1)^2*πω^2τ)*sin((2m+1)ωτ) =(4*A/π)*(-1/(2m+1)+sin((2m+1)ωτ)/(2m+1)^2ωτ) ということになり g(t)=(4*A/π)Σ(-1/(2m+1)+sin((2m+1)ωτ)/(2m+1)^2ωτ)*sin((2m+1)ωt) と表すことができる。 τ=π/8としてプロットしてみると wxplot2d([(4*((8*sin((5*%pi)/8)*sin(5*x))/(25*%pi)-sin(5*x)/5+(8*sin((3*%pi)/8)*sin(3*x))/(9*%pi) -sin(3*x)/3+(8*sin(%pi/8)*sin(x))/%pi-sin(x)))/%pi], [x,-5,5])$ 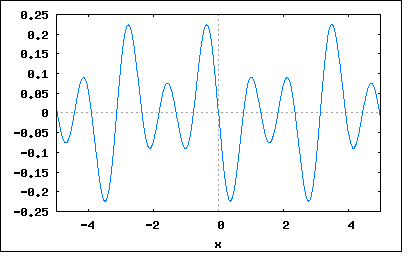 題意の台形波は上記2つの関数の合成なので y(t)=f(t)+g(t) =(4*A/π)Σ(sin((2m+1)ωt)/(2m+1))+(4*A/π)Σ(-1/(2m+1)+sin((2m+1)ωτ)/(2m+1)^2ωτ)*sin((2m+1)ωt) =(4*A/π)Σ(sin((2m+1)ωτ)/(2m+1)^2ωτ)*sin((2m+1)ωt) =(4*A/πωτ)*(sin(ωτ)*sin(ωt)+(sin(3ωτ)/3^2)*sin(3ωt)+(sin(5ωτ)/5^2)*sin(5ωt)+...) ということになる。これは著者の解と同じ。 5次までの高調波をプロットしてみると wxplot2d([(32*((sin((3*%pi)/8)*sin(3*x))/9+sin(%pi/8)*sin(x)+sin((5*%pi)/8)/25))/%pi^2], [x,-5,5])$ 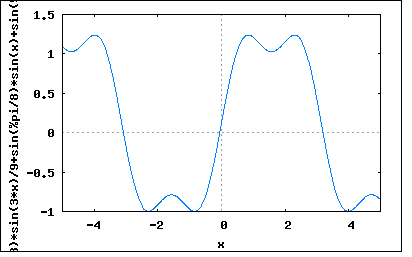 ちょっと収束が甘いけど台形に近づいてはいる。 P.S 良く見るとg(t)のFourier級数展開はy(t)-f(t)の形をしている。つまり極性を反転した矩形波に目的の台形波を重ね合わせたものになっている。考えてみれば当たり前だが。 |
| webadm | 投稿日時: 2009-8-20 6:58 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【10】ノコギリ波のFourier級数展開(その3) 前問の続きで、前問で得られたFourier級数展開の信号をRL直列回路に加えた場合の抵抗Rで消費される電力を求めよというもの。
ひずみ波の消費電力はFourier級数展開の基本波と高調波の振幅を起電力とする電源が重ね合わされたものと考えることができる。 回路に流れる電流の実効値は各電源毎に流れる電流の実効値の重ね合わせで表すことが出来るので I=(1/2)b0/R+Σ(an/(√2*sqrt(R^2+n^2*ω^2*L^2))+bn/(√2*sqrt(R^2+n^2*ω^2*L^2))) 前問では b0=bn=0, an=-(2*A/nπ)*(-1)^n であったので I=Σ(-(2*A/nπ)*(-1)^n/(√2*sqrt(R^2+n^2*ω^2*L^2))) 従って抵抗Rで消費される電力も重ね合わせの理によって Pa=Σ((-(2*A/nπ)*(-1)^n/(√2*sqrt(R^2+n^2*ω^2*L^2)))^2*R) =(2*A^2*R/π^2)*Σ(1/(n^2*(R^2+n^2*ω^2*L^2))) ということになる。 |
| webadm | 投稿日時: 2009-8-19 2:40 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【9】ノコギリ波のFourier級数展開(その2) 以前にも出てきたノコギリ波のFourier級数展開問題。こんどのはどちらかというとデューティ比が100%の三角波ともいうべきもので、これを半波整流すると前に出てきたノコギリ波になる。
通常通りFourier級数を解析的に求めるだけだと著者の解法とまったく変わりないので、違う方法でやってみよう。 Fourier級数もFourier変換と同様に重ね合わせ(Superosition)が適用できる。すなわち y(t)=f(t)+g(t) の場合そのFourier級数とFourier係数は y(t)=(1/2)b0+Σ(an*sin(nωt)+bn*cos(nωt)) an=(2/T)∫y(t)*cos(nωt)dt =(2/T)∫(f(t)+g(t))*cos(nωt)dt =(2/T)∫f(t)*cos(nωt)dt+(2/T)∫g(t)*cos(nωt)dt bn=(2/T)∫y(t)*cos(nωt)dt =(2/T)∫(f(t)+g(t))*cos(nωt)dt =(2/T)∫f(t)*cos(nωt)dt+(2/T)∫g(t)*cos(nωt)dt と表されるので、Fourier係数はそれぞれの関数のFourier係数の和となる。 前のノコギリ波の場合は f(t)=(2/T)*A*t (0≦t≦T/2) =0 (T/2≦t≦T) これは半波整流された正極性の部分だけだが、逆極性の分は g(t)=0 (0≦t≦T/2) =-(2/T)*A*(T-t) =-f(T-t) と表すことができる。題意のノコギリ波はこの2つの関数の合成として表すことができるので y(t)=f(t)+g(t) 既にf(t)に関するFourier係数は前の問題で求めているので、g(t)に関するFourier係数を求めて合成すれば良いことになる。 a'n=(2/T)∫g(t)*sin(nωt)dt (T/2≦t≦T) =(2/T)∫(-(2/T)*A*(T-t))*sin(nωt)dt =(2/T)∫(-2A+(2/T)*A*t)*sin(nωt)dt =-(4*A/T)∫sin(nωt)dt+(2/T)∫(2/T)*A*t*sin(nωt)dt (T/2≦t≦T) =-(4*A/T)*(cos(nωT/2)/nω-cos(nωT)/nω)+(2*A/T)*((sin(nωt)-nωT*cos(nωt)/n^2ω^2-(2*sin(nωT/2)-nωT*cos(nωT/2))/2*n^2*ω^2)) ここで ω=2π/T を代入すると a'n=-(2*A/πn)*(cos(πn)-cos(2πn))+(A*T/2π^2*n^2)*(sin(2πn)-sin(πn)+πn*(cos(πn)-2*cos(2πn))) =(2*A/πn)*(1-(-1)^n)+(A/π*n)*((-1)^n-2) =(A/πn)*(2-2*(-1)^n+(-1)^n-2) =-(A/πn)*(-1)^n (n=1,∞) また b'0=(2/T)∫g(t)dt (T/2≦t≦T) =(2/T)∫(-(2/T)*A*(T-t))dt =(2/T)∫(-2A+(2/T)*A*t)dt =-(4*A/T)∫dt+(4*A/T^2)∫tdt =-2*A+3*A/2 =-A/2 同様に b'n=(2/T)∫g(t)*cos(nωt)dt (T/2≦t≦T) =(2/T)∫(-(2/T)*A*(T-t))*cos(nωt)dt =(2/T)∫(-2A+(2/T)*A*t)*cos(nωt)dt =-(4*A/T)∫cos(nωt)dt+(4*A/T^2)∫t*cos(nωt)dt =-(4*A/nωt)*(sin(nωT)-sin(nωT/2))+(2*A/n^2*ω^2*T^2)*(2*nωT*sin(nωT)+2*cos(nωT)-nωT*sin(nωT/2)-2*cos(nωT/2)) ここで ω=2π/T を代入すると b'n=(2*A/πn)*(sin(πn)-sin(2πn))+(A/π^2*n^2)*(2πn*sin(2πn)+cos(2πn)-πn*sin(πn)-cos(πn)) =(A/π^2*n^2)*(cos(2πn)-cos(πn)) =(A/π^2*n^2)*(1-(-1)^n) =2*A/π^2*n^2 (n=1,3,5,...) =0 (n=2,4,6,...) 従ってg(t)のFourier級数展開は g(t)=-A/4+(A/π)*(sin(ωt)-sin(2ωt)/2+sin(3ωt)/3+...)+(2*A/π^2)*(cos(ωt)+cos(3ωt)/3^2+...) それに対して前の問題で求めた正極性側のFourier級数展開は f(t)=A/4+(A/π)*(sin(ωt)-sin(2ωt)/2+sin(3ωt)/3+...)-(2*A/π^2)*(cos(ωt)+cos(3ωt)/3^2+...) 従ってこの2つの合成波のFourier級数展開は y(t)=f(t)+g(t) =(2*A/π)*(sin(ωt)-sin(2ωt)/2+sin(3ωt)/3+...) ということになる。 Fourier係数をプロットすると wxplot2d([-(2*(-1)^n)/(%pi*n)], [n,1,5], [nticks,1])$ 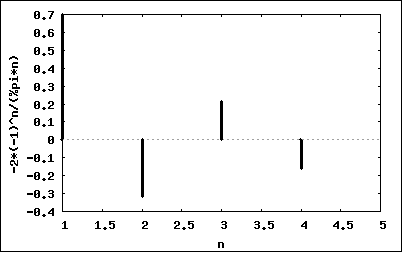 ということになる。 これは普通のスペクトルアナライザで表示されるものとは異なって極性が正と負がある。通常の測定器ではパワースペクトルを測定しRMS値で表示するためスペクトルはすべて正の値になる点に注意。その場合はすべての線スペクトルが2*A/πnの漸近線上にプロットされることになる。 P.S いつものことながら面倒な定積分はMaximaを用いて求めた。 重ね合わせを用いれば結構面倒な波形のFourier級数展開も容易に出来ることになる。 |
| webadm | 投稿日時: 2009-8-18 9:46 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
【8】奇数次高調波のみの波形 次ぎの問題ははなはだ曖昧な問い。
基本波、第三高調波、第五高調波からなる波形が時間軸上のある点で対称となるとき、その波形はどのように表されるか? というもの。問題は対称という意味が曖昧なのだが、ひずみ波で波形が対称性となるのは ・対称波 ・奇関数 ・偶関数 の3種類である。それぞれについて可能性を調べてみよう。 対称波という意味であれば y(t+T/2)=-y(t) となる点があるはず。 y(t)=(1/2)b0+Σ(an*sin(nωt)+bn*cos(nωt)) とすれば、基本波と第三高調波、第五高調波からなる場合 y(t)=(1/2)b0+a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+b1*cos(ωt)+b3*cos(3ωt)+b5*cos(5ωt) と表すことができる。一方対称となるためには y(t+T/2)=(1/2)b0+a1*sin(ω(t+T/2))+a3*sin(3ω(t+T/2))+a5*sin(5ω(t+T/2))+b1*cos(ω(t+T/2))+b3*cos(3ω(t+T/2))+b5*cos(5ω(t+T/2)) ここで T=2π/ω を代入すると y(t+T/2)=(1/2)b0+a1*sin(ω(t+π/ω))+a3*sin(3ω(t+π/ω))+a5*sin(5ω(t+π/ω))+b1*cos(ω(t+π/ω))+b3*cos(3ω(t+π/ω))+b5*cos(5ω(t+π/ω)) =(1/2)b0+a1*sin(ωt+π)+a3*sin(3ωt+3π)+a5*sin(5ωt+5π)+b1*cos(ωt+π)+b3*cos(3ωt+3π)+b5*cos(5ωt+5π) =(1/2)b0-a1*sin(ωt)-a3*sin(3ωt)-a5*sin(5ωt)-b1*cos(ωt)-b3*cos(3ωt)-b5*cos(5ωt) 従ってb0=0の場合 y(t+T/2)=-y(t) が成り立つので y(t)=a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+b1*cos(ωt)+b3*cos(3ωt)+b5*cos(5ωt) wxplot2d([sin(5*t)+cos(5*t)+sin(3*t)+cos(3*t)+sin(t)+cos(t)], [t,-5,5])$ 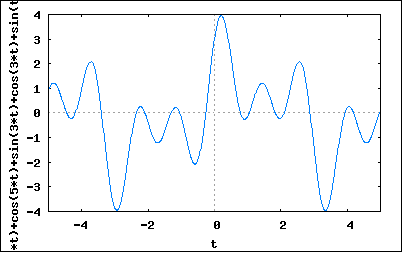 ということになる。 今度は奇関数波である場合を検討してみよう。 奇関数では y(t)=-y(-t) が成り立つ必要から -y(-t)=-(1/2)b0-a1*sin(-ωt)-a3*sin(-3ωt)-a5*sin(-5ωt)-b1*cos(-ωt)-b3*cos(-3ωt)-b5*cos(-5ωt) =-(1/2)b0+a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)-b1*cos(ωt)-b3*cos(3ωt)-b5*cos(5ωt) 従ってb0=b1=b3=b5=0であれば題意の条件を満たす。 y(t)=a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt) wxplot2d([sin(5*x)+sin(3*x)+sin(x)], [x,-5,5])$ 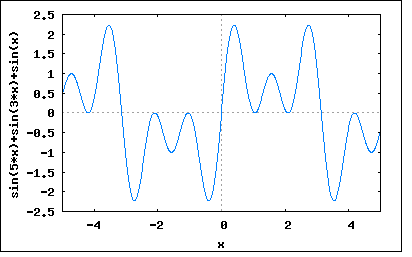 残りの偶関数の可能性をチェックしてみよう。 偶関数なら y(t)=y(-t) が成り立つ必要があるので y(-t)=(1/2)b0+a1*sin(-ωt)+a3*sin(-3ωt)+a5*sin(-5ωt)+b1*cos(-ωt)+b3*cos(-3ωt)+b5*cos(-5ωt) =(1/2)b0-a1*sin(ωt)-a3*sin(3ωt)-a5*sin(5ωt)+b1*cos(ωt)+b3*cos(3ωt)+b5*cos(5ωt) 従ってa1=a3=a5=0なら題意の条件を満たすことになる。 y(t)=(1/2)b0+b1*cos(ωt)+b3*cos(3ωt)+b5*cos(5ωt) wxplot2d([cos(5*x)+cos(3*x)+cos(x)], [x,-5,5])$ 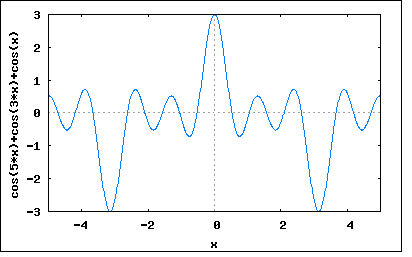 著者の解では題意をある時間を原点として点対称となる奇関数の意と解釈し、それだけを検証している。 P.S あとで良く考えたら対称波の検証の際に-y(t)とy(t+T/2)を比較すべきところをy(t)とy(t+T/2)と比較してしまっていた。訂正してお詫びする。 |
| « 1 ... 4 5 6 (7) 8 » | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

