| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-7-29 8:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
定K形帯域フィルタの設計 次は定K形帯域フィルタに関する問題。
公称インピーダンスR=600[Ω]、遮断周波数fl=1[kHz],fh=10[kHz]の定K形帯域フィルタを設計せよ。 というもの。 定K形帯域通過フィルタ(半回路)についてスクラッチから解析してみよう。 定K形フィルタなので であるのは一緒。帯域通過フィルタの場合には、Z1はすくなくともひとつ以上の共振点をもつLC直列回路となり、Z2はその逆回路でひとつ以上の反共振点を持つLC並列回路という構成になる。Z1が決まれば上の関係式から自ずとZ2も定まることになる。 従ってL1,C1,L2,C2とRの間には以下の関係が成り立つ 問題は帯域通過フィルタの場合には遮断周波数が2つ以上存在するということだ、それはどうやって定まるのだろうか? とりあえず影像インピーダンスを求めてみる必要がある。上記の式に基づいて以下構成の定K形帯域通過フィルタの影像インピーダンスを解析することにする。 上の回路の影像インピーダンスを四端子定数から導出すると ということでZi1の零点と極はZi2の極と零点に対応する。ω=0を除いた極と零点の周波数(ω1,ω3)が影像インピーダンスが実数と純虚数の境界点となる遮断周波数ということになる。ω1<ω<ω3の範囲ではZi1,Zi2はともに実数をとり通過域となる。それ以外では純虚数となり減衰域となる。ほとんどの参考書では遮断周波数(ω1,ω3)の式は複雑なので示していない。 同様に四端子定数から影像伝達定数を求め、減衰定数と位相定数を解析すると ということになる。 (2011/9/3) 影像伝達定数の式を導出時の形式を維持するように修正した。sqrt((o^2-o1^2)*(o^2-o3^2))=sqrt(o^2-o1^2)*sqrt(o^2-o3^2)は実数関数では常に成り立つが複素関数では常に成り立つとは限らないからである。境界周波数ω1,ω3は影像伝達定数の不連続点であるため解析接続を行う必要があった。このことに関して触れている書物は見あたらない。 従ってω1,ω2,ω3の関係からC1,L1,C2,L2は ということになる。整然と式が導出されるのはなんとも不思議でトリッキーだ。特にω1ω3=ω2^2という関係はなかなか気づかない。 これで公称インピーダンスRと2つの遮断周波数が与えられれば素子定数が定まることになる。 ということになる。 よく見たら問題文では周波数特性は問われていなかった。おそらく大変だからだろう。 確認のために減衰定数と位相定数をプロットしてみよう。 意図した通りである。厳密には遮断周波数近傍では実際の素子定数で計算すると微妙な計算誤差(実数を浮動小数に変換することによる誤差に起因する)があるが無視できる範囲である。 P.S 手元の複素関数論や複素解析の本を読み直してみたら、0≦ω≦ω1、ω1≦ω≦ω3それにω3≦ωのそれぞれの範囲で連続で正則な関数がω1とω3の不連続点で接続することは解析接続のことだと了解した。それまでは具体例が示されていないため(数学の本ではめったに具体例を挙げることはない)釈然としなかったが、そういうことだったのかと。ω1やω3は不連続点で一種の特異点であるが、前後の領域でそれぞれ正則な関数が同じ値をとるため、"除去可能"な特異点と呼ばれることも初めて意味を理解した。 |
| webadm | 投稿日時: 2011-7-31 0:28 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
続:定K形帯域フィルタの設計 前問は帯域通過フィルタであったが、今度は帯域除去フィルタ。
公称インピーダンスR=600[Ω]、遮断周波数fl=1[kHz]、fh=10[kHz]の定K形帯域除去フィルタを設計せよ。 帯域除去フィルタは帯域通過フィルタの逆回路であるので、同じ遮断周波数と公称インピーダンスを持つ前問の回路のZ1,Z2を取り替えればいいだけである。 本当かどうか検算のために、スクラッチから定K形帯域除去フィルタを解析してみよう。 定K形フィルタの条件式と回路構成から なる関係が成立する。 定K形帯域除去フィルタの回路から伝送行列を導くと ふう、Maximaに頼らずに自分でやったら式がすっきりした形となった。Maximaは有理式の分子の式を因数分解が苦手のようだ。 これまでとは違うのは、開放電圧伝達係数(A)の分母が4次式となっており、二次式の自乗となっている点である。この時点でs^2=-ω^2であっても自乗されるため分母は常に正の値となる点に注意が必要だった。 この点に気をつけて影像インピーダンスの式を導出すると 従ってZi1,Zi2ともにω=0とω=∞で公称インピーダンスRと等しくなり、ω1,ω2,ω3に零点と極をそれぞれ持つ。 著者が理論のところで示している影像インピーダンスの式とはMaximaを使って整理すると互いに同じ式であることは確かめることが出来た。しかしどうやったら著者の示す式様なエントロピーの低い式に変形する試みは失敗に終わっている。それは読者の課題としよう( ´∀`) 同様に注意を払いながら伝送行列の影像伝達定数から減衰定数と位相定数を導くと (2011/8/27)絶対値表記を止めてω>ω2の場合のケースを修正。トリッキーだが、Ln(j)=jπ/2,Ln(-j)=-jπ/2であることを利用した。Lnは複素自然対数関数(ln)の主値を与える関数である。 (2011/9/4) 解析接続される区間が臨界各周波数(ω1,ω2,ω3)でオーバーラップするように訂正。f1,f2,f3,f4が区間D1,D2,D3,D4でそれぞれ正則な関数であるとすると、それらが区間D1∪D2∪D3∪D4で解析接続された正則な関数fであるためには、D1∩D2(≠φ)でf1=f2、D2∩D3(≠φ)でf2=f3、D3∩D4(≠φ)でf3=f4でなければならない。 素子定数はω1,ω2,ω3の関係式から魔法的に導かれ ということになる。 これで計算をしてみると ということになる。これは著者の解答と一致している。 周波数特性をプロットしてみると なんと著者が理論解説のところで図示しているプロットとは異なったプロットになってしまう。 おそらく著者が示す減衰域でのβ=π(f0<f<fhの場合)は間違いである。正しくはβ=-π/2でなければならない。 この件に関する決着をつけるのはまたしても読者の課題としよう( ´∀`) |
| webadm | 投稿日時: 2011-8-6 9:22 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
対称定K形フィルタ 次は理論のときにおさらいした対称T字およびπ形の定K形フィルタに関する解析問題。
下図に示す対称T形および対称π形フィルタの影像パラメータおよび減衰定数、位相定数を求めて、通過域、減衰域を示し、影像インピーダンスを遮断周波数を用いて表せ。ただし、Z1,Z2はいずれも純リアクタンスでZ1Z2=R^2の関係が成立するものとする。 今度は著者ともValkenburgとも違うやりかたでアプローチしてみよう。 対称定K形フィルタの伝送行列をFとした場合、その行列に関してゼロでない固有値λ、固有ベクトルxが存在すると仮定すると ということになる。従って対称定K形フィルタの伝送行列の固有値から影像伝達定数が得られたことになる。一方影像インピーダンスZiは上で解いた固有値を元の固有値固有ベクトル方程式に代入して固有ベクトルの成分に関して解けば ということになる。これで行列の固有ベクトルから影像インピーダンスを導くことができるのを確認できた。 あとは具体的な回路の4端子定数を求めて上記の式に代入し影像伝達定数から減衰定数と位相定数を解析すればよいことになる 対称T字形の伝送行列は 従って影像パラメータはそれぞれ ここでZ1はリアクタンスであるので、複素平面の虚軸上の値のみをとる。従ってZ1^2は0から-∞の値をとることになる。影像インピーダンスZiは実数と純虚数の範囲をとり、その境界点が遮断周波数ということになる。 一般的な定K形フィルタを考えると低域/高域通過フィルタの他に帯域通過/阻止フィルタも含まれる。前者の場合は、Z1は容量性リアクタンスか誘導性リアクタンスのどちらかかしか取らないのでZ1^2/4R^2=-1を満たす点は1つだが、後者はZ1が容量性リアクタンスを取る領域と誘導性リアクタンスをとる領域の場合でそれぞれにZ1^2/4R^2=-1を満たす点が存在することに注意を払わなければならない。それと減衰域で影像インピーダンスは純虚数になるが、複素べき根関数は多価関数なので二乗根の場合正負両方に分岐が生じる。減衰域での影像インピーダンスをプロットした例が参考書では少ないのはこのためだ。 定K形低域フィルタの場合、Z1=jωL、Z2=-j/ωCとすると遮断周波数ω0は ということになる。題意の通りに影像インピーダンスを遮断周波数を用いて表すにはZ1^2/4R^2を遮断周波数を用いて表す必要がある 高域フィルタの場合Z1=-j/ωC,Z2=jωLとして同様に計算すると ということになる。表現的には同一だが、Ωのが低域と高域でとで互いに逆数の関係になっている点に注意。 帯域通過フィルタの場合、Z1=jωL1-j/ωC1、Z2=1/(jωC2-j/ωL2)とすると 従って影像インピーダンスは ということになる。これは著者が理論の際に示している表現と等価である。ω2をうまく消去したのね。自分でやってみないとわからない。 同様にして帯域阻止フィルタの場合Z1=1/(jωC1-j/ωL1)、Z2=jωL2-j/ωC2とすると 同様に影像インピーダンスは ということになる。従って低域フィルタと高域フィルタの関係と同様に帯域通過と帯域阻止のΩは逆数の関係になる。 減衰定数αと位相定数βは少しやっかいだ。標準化された角周波数Ωを使って書き直すと (2011/8/25) だいぶここから先で詰まってしまっていた理由が判明してきた。何度も著者や先人のアプローチをなぞって終わりにしようかと誘惑にかられたが、理由がわかれば光が見えてきたも同然。 先に導出した影像伝達定数(θ)式は他の参考書では扱われていないユニークなものである。これは良く見ると ということでacosh(A)=θ=ln(A±√A^2-1)ということだった。これは数学公式集とかには必ず載っているが、±のところが一般には+になっている点が異なる。大抵の参考書の公式は実数関数としての逆双曲線余弦関数であるので結果も実数でしかも1より大きくなければならないということになるためだ。ここのところはほとんどの公式集では説明が省略されている。高木貞治の「解析概論」では実数関数だがcoshの逆関数の導出手順が説明されている(54. 指数関数と三角関数との関係 対数と逆三角関数)。手元にある工学者向けの複素解析の指南書「現代工学のための複素関数の微分と積分」では数学の複素解析本では華麗にスルーしている変な複素関数や式が例題として出てくるし、突然前触れもなく双曲線関数の逆関数の式が出てくる。そこには先に求めたのと同じ表現が出てきている。 引用:
これはまさしく高木貞治の「解析概論」にある通り、複素対数関数の主値(principal values)のみをとる対数関数をLogと頭文字を大文字としている。±の部分は多価関数である二乗根関数の値そのものであるので、そのままになっている。ところがやっかいの種である。どちらも解としてあると他方は矛盾する結果をもたらす。このあたりの議論はめったに本では見かけないが、検索すると実は数値計算の分野では良く知られている問題であることがわかる。数値計算ではすべての関数は一価関数でないと都合が悪い。そこでFortranやその他今日ありとあらゆる言語や数値計算プログラミングの世界では複素関数もすべて一価関数としてライブラリ化されている。その際に問題となるのがどのような分岐選択(branch cuts)をするかという点。それによってはシステムが異なると同じ結果が得られないことになる。嵌ったのはまさにここである。実は複素逆関数だけで一冊の本が出ているぐらい込み入って間違いを犯しやすいのだった。そこに嵌って抜けられなかった。 Reasoning about the elementary functions of complex analysis 以下の式は連続な実数や複素数領域ではどれも等価だが、離散的な実数値や複素数を取る浮動小数点表示の計算機で計算するときにはある条件では意図しない異常な値を返すことになる 最後の式はKahan氏によって提案されているものでひとつ前の式にある特異点z=-1を解消しその近傍でオーバーフローを引き起こし誤った結果をもたらすのを回避している。数値計算屋さんなら誰しも知っていることかもしれないが素人には区別がつかない。 The complex inverse trigonometric and hyperbolic functions なんの話だっけ。ああ、分岐選択の話ね。さてどうやって±を+にすればいいんだっけ。 検索で良く見つかるのはどれも実数関数としてのものであるがそのトリックが複素関数でも使える ということになる。つまり受動素子から成る二端子対回路の影像減衰定数は常に正で負になることは無い(回路に流入する電力より流出する電力が多くなるわけがない)からという理由で負号は排除できたということになる。一般的には依然としてcoshの複素逆関数の主値は二価であるが計算機プログラム(Maxima等)では一価関数で正の値のみ返すという具合。本当かどうかは読者の判断に委ねよう( ´∀`) さていよいよこれでT字形回路の周波数特性を解析することになる。影像インピーダンスの解析の時と同様に標準化された角周波数Ωを用いて書き直すと ということになる。よく見るとαのLn表現は2acosh(Ω)と同値であることがわかる。同様にβのatan表現はasin(Ω)と同値である、それを確かめるのは読者の課題としよう( ´∀`) (2011/9/4) 解析接続される3つの定義区間が境界点となる遮断周波数でオーバーラップしてなかったので訂正。区間D1,D2,D3でそれぞれ正則な複素関数f1,f2,f3が解析接続される場合、D1∩D2(≠φ)なる区間でf1=f2、D2∩D3(≠φ)なる区間でf2=f3でなければならない。 引用:
それにしても著者の解(i)はどう見ても間違いだろうというところが見受けられる。αが負を値を取るように示されている。これは絶対おかしいだろう。βが-πとなった時点でsin(β/2)は-1なのでcosh(α/2)は正の値をとらないといけない。しかも各区間が解析接続されてないし(;´Д`) これで標準化された角周波数Ωですべての対称T字定K形フィルタの周波数特性が得られることになる。 さてこれでやっと対称T形が終わった。あと対称π形が残っている(吐血) といっても既に対称回路の伝送行列に関する影像インピーダンス及び影像伝達定数は共通なので対称π形の定Kフィルタ回路の4端子定数のうち開放電圧減衰係数(A)さえ判ればあとは同様に事は進むと思われるのでさっさと終わらせてしまおう。 右の回路の伝送行列を導くと 従って開放電圧減衰係数(A)はT字回路と同じなので影像伝達定数は共通ということになり、標準化された角周波数Ωで統一的に表されることになる。 対称π形回路の影像インピーダンスは4端子定数BとCより ということになる。これはT字回路の場合とは零点と極がちょうど逆の関係にあることを意味する。 更に詳しい解析は読者に委ねよう( ´∀`) P.S 著者やValkenburg他多くの書では王道的なアプローチとして影像伝達定数の式を導いた際に という関係があることに着目し、双曲線関数の諸公式を利用して という関係式を得て、Ωに対するθの実数部(α)と虚数部(β)の挙動を解析する方法をとっている。 かつて直流回路で有限抵抗ラダー回路の解析の解で双曲線関数が登場して以来、双曲線関数は宿敵になっているので、なるべく対決を避けるために、あえて双曲線関数を使わないアプローチをとってみたが、裏街道を通って都を目指すようなもので思い返せば茨の道だった(ノД`) 結局は王道を通っても裏街道を通っても同じ結論に辿りつくのだが、王道を歩んできたはずの著者ですら最後にとんでもない間違いを犯して全部を無駄にしてしまっている。裏街道はもっと多難で、方向を誤る難所がいくつもあることがわかった。結果的に複素双曲線関数が複素対数関数に包含される以下の意味を理解した。 引用:
複素双曲線関数を用いた解析を避けて、むしろ難しい複素対数関数を用いた解析は振り返るとこちらが正道だろうという気がしてならない。双曲線関数を用いた解析は複素対数関数を使って最終的な答えを得てみたら逆双曲線関数や逆三角関数だったということで、もっと近道があるに違いないと戻って探して見つけた(それこそもってあまった)方法という気がしてならない。それでも著者やValkenburgですら道を誤る。かなり神経を使うのは確かで、何度も投げだそうと考えた。これは我々が複素関数に慣れていないという現れでもある。慣れてしまうと、「解析概論」や「現代工学のための複素関数の微分と積分」にあるようなトリックを理解することができる。 もってあまったような複素対数関数を使った定K形フィルタの解析は他では見あたらないので、オリジナル性が高いものと自負している(touch wood!) 結局は行き着くところ双曲線関数が待ち受けているということは、我々の住む宇宙は双曲線関数と密接なつながりがあるということを意味しているのだろうか? これも読者の永遠の課題としよう( ´∀`) P.S ここまでの演習問題ではいやと言うほど数学の複素関数解析で必ず教わる解析接続、多価関数について実践的に学ばされる結果となった。数学書を読んだり学生の時に講義を受けたときには具体例が無いためまったく実感がなかったが、ここにきて古典フィルタ理論でその理解が試されるとは予想もしなかった。 すでにいくつかの演習問題のところで後で高木貞治の「解析概論」や寺沢寛一の「数学概論」を読み返して数学的な視点を得て見直すべきところは訂正した。 おもしろいことに「解析概論」と「数学概論」の複素解析の部分を読み比べてみると、両者はその立ち位置がまったく異なっていることに気づかされる。 「解析概論」は数学者である高木貞治が書いたものであるから、数学者の卵もしくは数学の教養を得ようとする学生に向けられていることがわかる。特徴的なのは、第5章の"63. 解析的延長"と題された解析接続に関する記述が数ページに渡るほど熱の入れようなのに対して、「数学概論」は数学者でない寺沢寛一が自然科学を学ぼうとする学生や社会人向けに書かれたものなので、解析接続についてはどこの本にも見られるように1ページ程度にあっさりと触れているだけである。 「解析概論」の解析接続に関する記述は、証明のやり方やWeierstrass批判にまで突っ込んでいる最も高木貞治らしさが出ている部分のひとつでもある。これは是非とも読んで欲しいところではある。苦労して定K形フィルタの影像伝達定数の解析をやってみたら、これがまさに解析関数の解析延長(解析接続)そのものだったというのが読んで合点した次第。今は体に染みいるように書いてあることが良く理解できる。 引用:
一方「数学概論」の同じテーマの扱いも「解析概論」に負けずおとらずである。前者は後者が深く踏み込んでいない部分について多くのページを割いている。同じ第5章にある"5-8 多価関数の岐点"では多価性について数学者は決してしない具体例を挙げて解説している。年代的には後者は前者よりもずっと前に書かれているので、当然ながら敬意を払って記述範囲の棲み分けをしたと思われる。「解析概論」では明確には区別されていない代数的岐点、対数的岐点や、まったく登場しないRiemann面も異例の詳しさで説明されている。ちょうど「解析概論」で現代的に見ると残念な部分を補完しているように見える。 古典フィルタ理論を学ぶ時には「解析概論」や「数学概論」を一度読み直してみる良い機会かもしれない。いや必読に違いない。 手元には複素解析本の原典とも言うべきCOURANTが編纂した複数の複素解析書とHURWITZの楕円関数論の本を合本した分厚い古本がある。時々それを眺めるのだが(ドイツ語なので良く読めない)それには「解析概論」や「数学概論」に出てくるトピックス(元ネタ)が詳しく述べられているのが見てとれる。 |
| webadm | 投稿日時: 2011-8-29 2:14 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
対称π形高域フィルタ 次の問題は対称π形高域フィルタの影像インピーダンスと遮断周波数を求める問題。
回路の伝送行列を求めると 従って影像インピーダンスは ということになる。遮断周波数は影像インピーダンスが実数と純虚数をとる領域の境界点の角周波数ω0から ということになる。 |
| webadm | 投稿日時: 2011-8-30 16:35 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
対称T形帯域フィルタ 次は対称T形帯域フィルタの通過域を求める問題
ただしL=0.5[H],C=0.2[μF]とする 最初に解法のアプローチがいくつあるか考えることにしよう。 通過域はfl,fhの2つのクリチカル周波数を境界点としてfl≦f≦fhなる範囲である。 ひとつのアプローチはfl,fhがそれぞれ影像インピーダンスが実数と純虚数をとる領域の境界点であるのでそれを求める方法。これは著者が既に使用して答えを得ている。 もうひとつないだろうか? 以前の問題でたまたま対称T形帯域フィルタの解析の時に副産物として発見した境界周波数の以下の関係を利用する方法があった( ´∀`) これを使えば楽勝じゃないか( ´∀`) 境界角周波数ω0,ω1,ω2をそれぞれ境界周波数f0,fl,fhで書き直すと 上の式からfl,fhが解けることになる。 ということになる。 これに題意の素子定数を当てはめると ということになる。1uFは10^-6 Fであることに注意。 なんだ簡単じゃないか( ´∀`) |
| webadm | 投稿日時: 2011-8-31 17:17 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
3素子フィルタ 次の問題は初めて聞く3素子フィルタの影像インピーダンスをプロットし、遮断周波数を求めよという問題
ただしL=30[mH],C1=1[uF],C2=0.1[uF]とする。 今までの問題通り影像インピーダンスの解析問題であるのだが、定K形フィルタではなく3素子フィルタということだが、どちらも影像インピーダンスに基づいたフィルタであるのには違いない。 すでに伝送行列を求めて4端子パラメータから影像インピーダンスを導くアプローチは著者が解を示しているので、それ以外の方法でやってみよう。 影像インピーダンスは2端子対回路に共通なので、3素子回路のように素子数が少ない回路の場合には、影像インピーダンスを開放駆動点インピーダンスと短絡駆動点インピーダンスから求める方法を使ってみよう。 3素子フィルタは非対称回路なのでそれぞれの端での影像インピーダンスが異なる。Z1f,Z1s,Z2f,Z2sをそれぞれ端子対の開放および短絡駆動点インピーダンスとすると、それぞれの端子対の影像インピーダンスZi1,Zi2は ということになる。 回路からZ1f,Z1s,Z2f,Z2sを求めて上の式に代入すると ということになる。上記の式から影像インピーダンスが実数と純虚数をとる境界点はs=0とs=∞を除いたそれぞれの影像インピーダンスの零点と極であることは自明で ということになる。 従って遮断周波数は題意の素子定数を代入すると ということになる。 影像インピーダンスを周波数fを横軸にプロットしてみると (2011/9/4) 解析接続が明確になるように表記し直した。 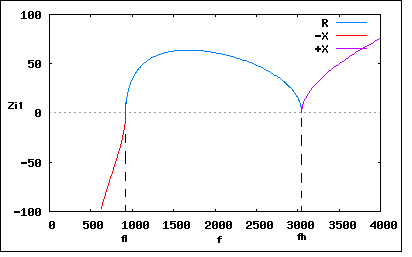 通過域ではちょっと卵の殻を半分に切ったようなカーブを描く。著者のプロットは左右対称な放物線のように描かれているが実際には対称ではない。減衰域では影像インピーダンスは純虚数をとり、同じ平面には本当は描けないが、虚数部をプロットしてみた。f<flでは容量性リアクタンス、f>fhでは誘導性リアクタンスとなり、f=0,∞に極を持つことに注意。 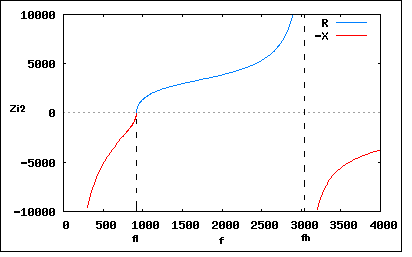 Zi2も通過域では影像インピーダンスが実数値をとり、f=flが零点でf=fhが極になる。減衰域ではともに容量性リアクタンスを取り、f=0に極を、f=∞に零点を持つ点に注意。 そういえば3素子フィルタを考案したのは誰なのだろう。この回路は逆向方向の影像インピーダンス特性はf=∞に零点を持つので高周波的にはよろしくない、どちらの方向でもf=∞に極を持つ対称T字回路にして使うのが良いだろう。そうするとシリーズに入っているLC共振回路はQの鋭い水晶発振子やセラミック共振子が使える。 これは今も随所で使われている3端子フィルタの原理そものでなかろうか。どことなく周波数特性も似ている。3素子フィルタの起源についても読者の自由研究課題としよう( ´∀`) P.S 解析接続の視点から見直して後半部分を書き改めた。影像インピーダンスの式は更に(例えばは標準化された周波数を用いて)書き直しても同じ結果が得られることを確かめるのは読者の課題としよう( ´∀`) P.S 次の問題で躓いた時にふと思い出したように開いてみたドイツの理論電気学の教科書に3素子フィルタの元ネタを偶然発見した。最初対称回路だったので気がつかなかったが、二等分すれば問題の回路と同じで3素子となる。 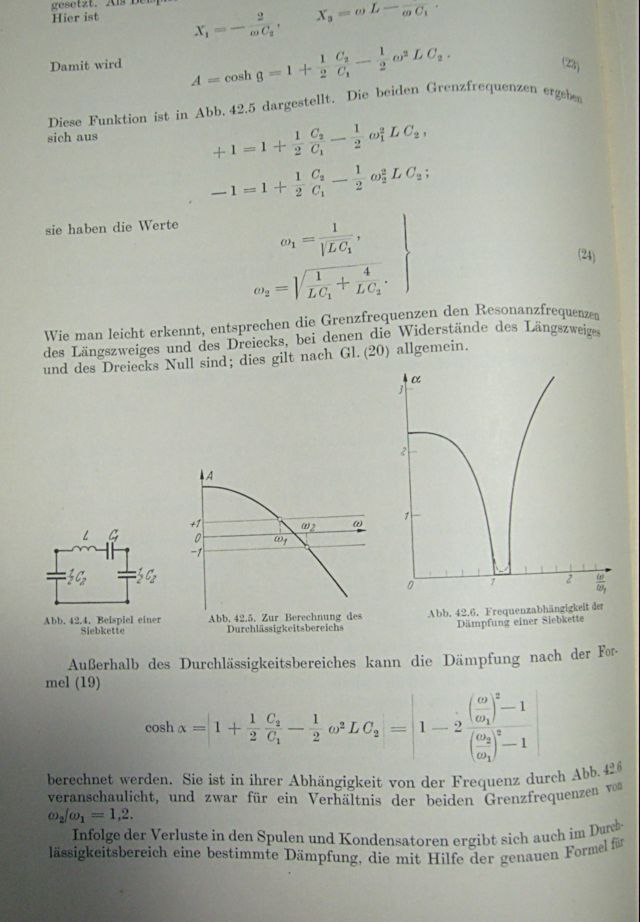 このドイツ定番テキストのすごい点は、巻末に載っている参考図書がすべてドイツ語の図書ばかり。戦前からそういう雰囲気は強かったけど、国粋主義をぷんぷん感じる。ドイツに遊学した数学者の高木貞治もそれをいやと言うほど体感したのだろう、そうした趣を批判しているが、「解析概論」ではまったく参考図書を挙げず、すべて持論であるかのようなテキストを書くという国粋主義に陥っている。当時はそういう雰囲気があったのがうらやましいと思うこともあるが、それが開戦を迎合する土壌を作ったという見方もできる。 本当に電気や電磁気学を学ぼうとする時にはドイツの理論電気学の教科書を座右に置くのも悪くないかもしれない。今も改版されて増刷されている。 |
| webadm | 投稿日時: 2011-9-4 22:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
続:3素子フィルタ 次の問題も3素子フィルタに関するもの。
上記の回路の遮断周波数をfl,fhとしたいとき、L,C1,C2をどのように選べばよいか、ただしf0=√(fl・fh)のときの終端抵抗をRとする。 というもの。一見すると前問の回路の逆回路のように思えるが、実は違う。前問の回路もそうだったが、定K形フィルタ回路から一素子(Lを)省いたような回路である。この話は昔Cauerの人となりと業績を紹介をした際に"従来知られているものよりもLがひとつ少なくてすむ"とかそのまま伝えられるまま書いた憶えがある。もしかしてそのことかもしれない。Cauerの著書や特許で出てきたものかもしれない。その追跡は読者の自由研究課題としよう( ´∀`) さて、問題であるが、題意が前問の逆問題である。今度は遮断周波数を与えられて、素子定数を求めるもの。同じようにはいかない。 ストラテジーとしては ・回路の影像インピーダンスから遮断周波数と素子定数の関係式を導く ・上記関係式と題意で与えられた条件から素子定数を解く というのが考えられる。と思ったらこれはすでに著者がやっている。 なので別のアプローチを考えよう。 ・回路の影像伝達定数から遮断周波数と素子定数の関係式を導く ・上記関係式と題意で与えられた条件から素子定数を解く というのをやってみよう。 影像インピーダンスと違って、影像伝達定数はどちらの方向でも同値なのでこちらの方が楽かもしれない。 回路の伝送行列をまず求めると 従って影像伝達定数は ということになる。従って通過域と減衰域の境界点が遮断周波数なので、影像伝達定数が純虚数(通過域)から複素数(減衰域)の境界角周波数(ω1,ω2)が遮断角周波数なので という関係式が得られる。 これだけでは未知数(C1.C2.L)に対して方程式がひとつ足らないのでまだ解けない。 わがんねー(ノД`) 著者の解は自分でも確認して魔法的に式の中から虚数単位が消滅するのを確認。 やっぱりf0で影像インピーダンスがRと同値になる条件を使うしかないのかな。 こっから余談。前問の逆回路のように見えるこの問題の回路は、実は前問の回路と同じく帯域通過特性を持っている。顕著な違いと言えば片方の影像インピーダンスがちょうど逆数になっていて、flとfhが前問では零点なのに対してこの問題の回路では極である。反対方向の影像インピーダンスはどちらも同じ様な特性で、flが零点、fhが極と共通している。 それが判ったからといってヒントが得られるわけではないけど、たった3素子の回路でも紙の上で解析すると1ページの計算用紙の裏と表を使っても足らない。それくらい面倒である。それだから大学では古典フィルタ理論を教えなくなってきたのかもしれない。教えてもついていけない学生ばかりだとすればなおさら。人の事は言えないが。 しかし本当に影像インピーダンスを計算しないと解けない問題なのだろうか、そこが問題だ。 しばらく見てなかったドイツの古い理論電気学の教科書に確かいろいろなフィルタ回路の周波数特性の一覧表が書いてあったと思い出し、開いてみたら同じところで3素子フィルタの元ネタが あった( ´∀`) 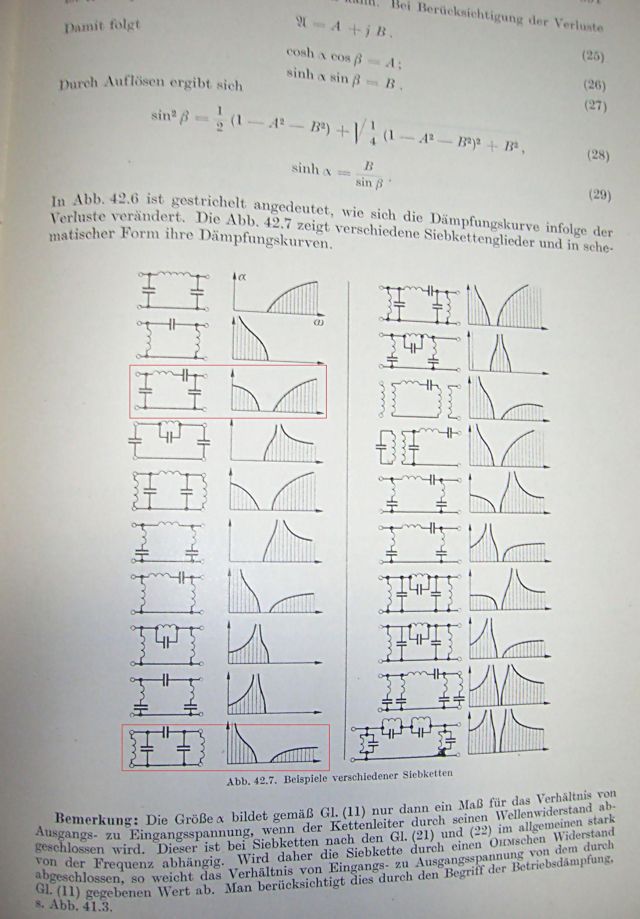 この教科書の巻末の参考文献リストはドイツ人によるドイツ語の書物だけだが、そこに戦後になってからようやく出版された有名なCauerの線型フィルタ理論の書や、線型フィルタを発見しドイツで先駆的な役割を果たしたWagnerの文献も載っている。おそらくそのどちらかから引用したものとおもわれる。つまりWagnerの頃に後のCauerやZobelのように意図的に導出できないにしろLBF,HPF,BPF,BEFがリアクタンス回路で構成できることが判っていたのである。理論的な裏付けはCauerをはじめ後生の人たちによってドイツと北米とで独自に行われていった様子がうかがい知れる。その間に第二次世界大戦があった。 対称π形回路なのですぐに気づかなかったが、一覧表の中に様々な対称形フィルタ回路の減衰特性があり、問題の回路と同じ帯域通過特性を持ち逆L字回路に二等分可能である。 良く考えたら、3素子フィルタ回路は誘導M形フィルタのZ1とZ2を入れ替えたような回路でもある。ということは3素子フィルタというのは実は誘導M形フィルタの帯域通過版なのだろうか。すなわち3素子フィルタは帯域通過形の定Kフィルタをプロトタイプとする誘導M形フィルタではなかろうかという仮説である。それを調べるのは読者の課題としよう( ´∀`) 前は記述が難しいので良く読んでなかったが、以前の問題で発見したような事が視点や表現は異なるものの解説されていた。 そこでアイデアが思いついた、対称回路にしてしまえば、両端で同じ影像インピーダンスになるのだから 2つの半回路を接続し対称π形回路にすればf0で影像インピーダンスZiがRに等しくなるのなら、反対側から見た駆動点インピーダンスもそれと等しくなるはずである。そこからもうひとつの条件式が導かれる。 ずいぶんと見通しが良い方法じゃないか( ´∀`) 厳密的な意味では影像インピーダンスを用いていないとは言えないのだが、アプローチとしては異なるのでよしとしよう。 上の回路図の電源から見た駆動点インピーダンスを求めると ということになる。これをRに関して解くと という驚くべき関係が成り立つことになる。この時点でもうLについて解けたも同然( ´∀`) 先のω1、ω2,の関係式に順次代入して残りの素子定数について解くと ということになる。 やったよママン(ノД`) 諦めずに続けた甲斐があったよ。長い便秘が解消した気分( ´∀`) P.S 著者は影像インピーダンスの条件式から最初にLを導いているが、こちらのアプローチではLについて解くよりも暗算でも出来る程度に楽であったからだ。 |
| webadm | 投稿日時: 2011-9-10 19:28 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
反定K形フィルタ? 次の問題は容量性か誘導性いずれかのみからなるフィルタ回路に関するもの。
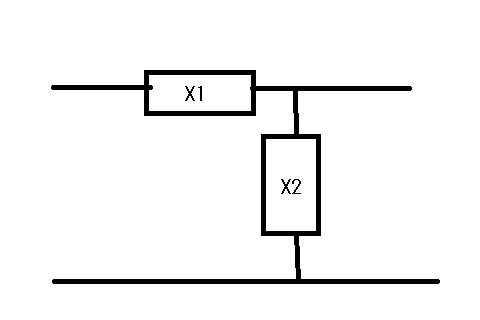 X1,X2がともに容量性もしくは誘導性リアクタンスの場合、以下の条件を満たす時にフィルタ特性を有することと、通過域と遮断周波数を求めよというもの。 リアクタンス素子のみから成る二端子対回路は、そのインピーダンス行列が歪Helmite行列(行列要素がすべて純虚数)になることから、どちらも数学的には共通の性質を有することは容易に想像できる。 特に著者はこの回路が何と呼ばれるかは教えてくれていないが、勝手に定K形フィルタとはZ1Z2が負の実数になることから反定K形フィルタと呼ぶことにしよう。本当はどうなのかは謎、定K形フィルタの一種に数えてもよいのかもしれない。Z1Z2が定数になるという意味では一緒だから。 実務でも高周波回路ではコンデンサだけからなるフィルタ回路は有用である。インダクタンスは作るのが面倒だし、内部抵抗と浮遊容量結合を伴うので、理想的なインダクタンスとはならないからだ。コンデンサそのものも実際には漏れコンダクタンスを伴うしリード線がインダクタンスを持つが、チップコンデンサならそうした要素は低減できる。なので挿入損失の少ない実用的な高周波フィルタができる。 フィルタ特性を有するか否かは映像伝達定数の減衰定数を調べればすぐにわかる。映像伝達定数は二端子対回路であれば4端子定数を使って共通に表され ということになる。従って遮断周波数は通過域と減衰域の境界点の条件 を満たすリアクタンスX1をとる周波数ということになる。X1が誘導性リアクタンスの場合 ということになる。同様にX1が容量性リアクタンスの場合 ということになる。 著者の解と同じようにはなったが、途中で矛盾点に気づいた。 題意のX1,X2がリアクタンスだとすると、X1,X2は共に誘導性もしくは容量性のいずれかで正か負の実数をとるからX1X2は常に正の実数となる。しかし題意ではX1 X2=-R^2と負の実数をとるとしている。これが第一の矛盾点である。 しからば題意のX1,X2がインピーダンスだと解釈すると、X1,X2は共に誘導性もしくは容量性のいずれかで正もしくは負の純虚数となり、X1X2は常に負の実数となるのでX1X2=-R^2としても矛盾はない。しかしそうすると、今度は映像伝達定数が常に実数となってしまう第二の矛盾点を生じる。回路はフィルタ特性ではなく減衰器の特性を持つことになってしまい題意に即さない。 この問題は題意に矛盾点があり、その矛盾の故に数式上ではフィルタ特性が得られるというものである。 実際にキャパシタもしくはインダクタンスだけを用いて回路のような逆L字回路を構成すると、それはちょうど抵抗で逆L字回路を構成したのと同様にフィルタではなくアッテネータの特性を示すことになる。 変な問題で頭を悩ましてしまった。頭が変になるところだったよ(;´Д`) P.S 嘘だと思ったら著者の解の映像インピーダンスの式がX1<Rの時にどんな値をとるか計算してみるとよい。映像インピーダンスが負の実数(負性抵抗)をとることを確認できるだろう。それはそうした映像インピーダンスを持つ二端子対回路が受動素子だけでは実現できないことを意味する。これが第三の矛盾点である。 すなわちこの問題の題意は ・2つの負性抵抗からなる逆L字回路はフィルタ特性を有する ということを確認しその遮断周波数を求めよということだったというわけである。これはちょっとひねり過ぎていないだろうか? |
| webadm | 投稿日時: 2011-9-12 4:11 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
対称格子形回路 前問はひどかったが、今度はまともな問題。
以下の様な対称格子形回路はどのようなフィルタとなりうるかというもの。 対称格子形回路にはそれと等価な対称T形もしくは対称π形回路が存在することを二端子対回路の時にちらっと学んだ記憶がある。つまり対称二端子対回路には平衡形と非平衡形の2つのトポロジーが存在するということである。 問題の対称格子形回路と等価な開放および短絡駆動点インピーダンスを持つ以下の対称T字回路が存在すると仮定すると それぞれ回路の開放および駆動点インピーダンスが等しいことから これをZ1,Z2に関する連立方程式として解くと ということになる。後のはZ2に負の係数が伴うなので受動素子では実現できないため除外する。 これは以下の回路と等価であることを意味する 等価な対称π形回路も存在するだろうか、それを確かめるのは読者の課題としよう( ´∀`) 対称T字回路なら伝送行列も簡単に得られる。 従って影像伝達定数は ということで大変なことになったが、ω0が減衰域と通過域の境界点の周波数になるので、それが遮断周波数ということになる。 回路としては高域通過フィルタ特性を有していて、減衰域のω∞に減衰極を有する。ω2で通過域での位相定数が-π/2となる。ω∞とω2はω0を中心にω1で決まるちょうど対称位置の関係にある。 素子定数C0,C,Lをそれぞれω1<ω∞<ω0<ω2の関係を保つように決めて周波数特性をプロットしてみると あれ妙だな。ω=0が極にならない。 著者の解を見てみると、coshθの式の導出の途中で間違えていて、どう考えてもZ2+Z1をZ2*Z1として勘違いして計算しているが、偶然の誤りからω=0、ω∞に極を持つ特性の式が得られてしまっている。 引用:
これは明らかに著者のミスである。著者が流用している第二章問題【30】の結果から計算しなおしても、こちらのアプローチで得た結果と一致する。 どうすんだこれ(´Д`;) 仕方ないので、基本に戻って4端子定数の条件から直接伝送行列の要素を導いていこう。 ということになる。なんだ合ってるじゃないか( ´∀`) 以前の問題で紹介したドイツの参考書の各種フィルタ特性の一覧表のなかに、上の等価回路と同じ反回路を対称π形回路にしたものが載っている。それを見るとやはりω=0は減衰極ではなく有限値をとる。 不思議だがプロットしてみよう C=1[F],C0=10[F],L=1[H]とした場合、 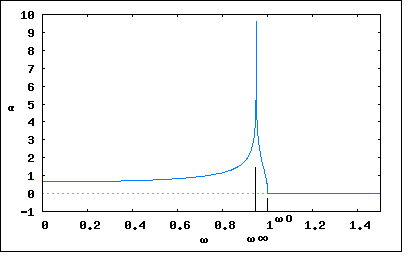 ということになる。これを正解としよう。 プロットに負のαの領域が含まれているように表示されているが、これはαの零点近傍で計算誤差が生じているためで、拡大していくとどんどん誤差は小さくなる。 これは高域フィルタと言えるのだろうか、特性的には確かにフィルタだけど。減衰量が極を除いては微々たるものだ。どちらかというとノッチフィルタに近いものがある。そういえば、対称格子形回路はブリッジ回路だった。それだ。 P.S 通勤バスに乗っている間に思い返してみたら気づいたのだが、上の等価回路はC0≧Cの場合だが、C0<Cのケースがすっぽり抜けていた。 問題の対称格子形回路はC0=0の場合は、2つのLC直列共振回路がシリーズに入った二端子対回路となる。C0が0でない場合に、C0≧Cのケースでは先の解析通りの周波数特性になるが、C0<Cの場合は状況が一変する。まず減衰定数の極ω∞が虚軸上に移る。依然としてω=0は極ではない。周波数特性はどうなるのだろう。 基本的にωが実数のみを取る以上、分母が0となることはなく極が現れないことになる。C0<Cの場合の減衰定数をプロットすると 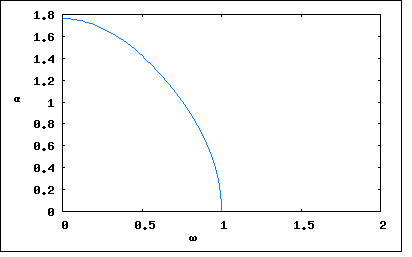 ということになる。ω0が零点であることには変わりない。 C0=Cの場合のみω=0に極を持つ。 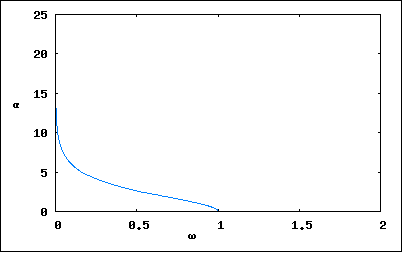 なんとも奇妙な回路である。更なる研究は読者の課題としよう( ´∀`) |
| webadm | 投稿日時: 2011-9-17 9:39 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3095 |
対称T形低域フィルタ ふう、このところ立て続けに難問が続いたが、今度は一見すると易しそうな問題。
以下の対称T形低域フィルタの影像パラメータを求め、遮断周波数をωlとするとき、ω≪ωlが成立する範囲での遅延時間τを求めよというもの。 見たところ逆L字形回路に二分割すると定K形フィルタだというのがわかる。確か以前の問題で既に解析済みである。 念のために伝送行列を求めると 対称回路なので、伝送行列の固有値と固有ベクトルから影像パラメータを導くと ということで理論のとこで学んだ対称T形定Kフィルタそのものであることが確認できた。 あとは題意にある遅延時間だが、これの定義はどうしたものだろう? 位相遅延(τp)という定義であれば、位相定数をωで割ったもの。 群遅延(τg)という定義であれば、位相定数をωで微分したものである。 位相定数が関係しているが、区間によって異なるが、ω≪ωlに限ってしまえば通過域なので ということになる。 このような限定した位相変位区間での線型近似はアナログ信号処理回路では良く用いられるテクニックである。線型近似できれば、対応する線型回路が存在するためシンプルな実現可能な回路で設計できるしその解析も容易である。しかし想定よりも大きく位相が広範囲に変化する場合には、そうした回路は当初の意図した通りには動作しないので注意が必要である。 位相遅延や群遅延もフィルタ回路の重要な特性である。一般にそれらは平坦であるのが好ましい。 |
| « 1 (2) 3 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

