| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-11-5 10:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:断続部の有るRL直列回路 RL並列回路の問題が続くと思いきや、RL直列回路に逆戻り。
今度は電圧を加えた時と取り去った後の過渡現象を解析するもの。 図の回路において、t=0でスイッチS1を閉じ、ついでt=TのときスイッチS2を閉じると同時にスイッチS1を開くものとする。この回路に流れる電流iおよびインダクタンスLの端子電圧eLを求め、これを図示せよ。 というもの。 これは比較的簡単かもしれない。 まずはt<Tの場合 Lに流れる電流をiとしてその電圧降下をuとすると という関係が成り立つ。 従って第一の式を微分したものに第3の式を代入するとuに関する線型同次一階微分方程式が得られる これを解くとuの一般解は ということになる。初期条件としてt=+0の時にu(+0)=Eとおけば特別解は ということになる。今度はこれを最初の式に代入すればiが解ける ということになる。なんだ簡単じゃないか(´∀` ) 残るはt>Tの場合、電源電圧がEから0に変化したのと同じ意味なので電流iに関して以下の関係が成り立つ 同次形なのでこれの一般解は ということになる。特別解は初期条件としてt=+Tの時にi(+T)がそれ以前のi(T)と等しいと置けば ということになる。従ってuは ということになる。 E=R=L=T=1としてuとiをそれぞれプロットしてみると 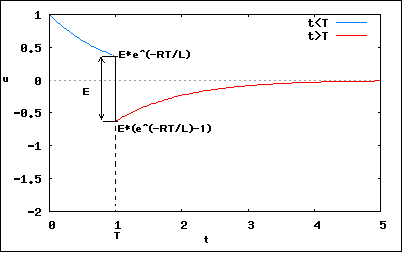 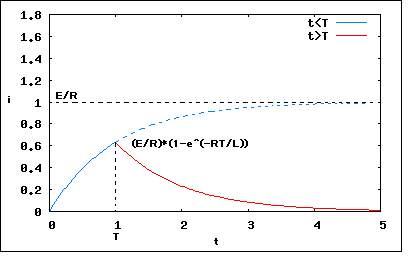 ということになる。 P.S t>Tの場合にuに関する微分方程式をたてても導けるはずだがどうもうまくいかなかった。これは読者の課題としよう(´∀` ) (続く) |
| webadm | 投稿日時: 2011-11-5 20:42 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
まだまだ:断続部の有るRL直列回路 更に続くRL直列回路、いささか食傷気味
しかしこれはスイッチング回路の面白い問題。 図の回路において、電流iがi1に達したときスイッチを開き、iがi2に低下したときに閉じることを繰り返すものとする。十分に時間が経過した後のスイッチを開閉する周期Tを求めよ。 というもの。 面白いだけにちょっと難しい。 スイッチを閉じると定常電流がE/(R1+R2)からE/R2に変化するのでそこへ向かって連続的に電流が増加していく。電流がi1に達すると今度はスイッチが開いて定常電流E/(R1+R2)に向かって電流が連続的に減っていきi2に達すると再び電流が増加していく。i1,i2も有限時間内に達する必要から定常電流値とは異なる必要がある。つまり定常状態でスイッチが開閉するわけではないのだ。つまり という関係になる。 スイッチが閉じている間は以下の関係が成り立つ これを解くと一般解は ということになる。初期条件としてt=+0の時にi=i2とすると ということになる。また電流がi1に達するt=T1には以下の関係が成り立つ 従ってi2からi1への遷移時間T1は ということになる。 一方スイッチが開いている間は以下の関係が成り立つ これを解くと一般解は ということになる。初期条件としてt=+T1でi1と等しいとおくと ということになる。t=T2で電流が再びi2に達するとすると以下の関係が成り立つ 従ってこれをT2に関して解くと ということになる。 従って周期TはT2であるので上の式に先のT1の式を代入すると ということになる。 R1=R2=L=1,i1=0.8,i2=0.6とした場合のグラフをプロットすると 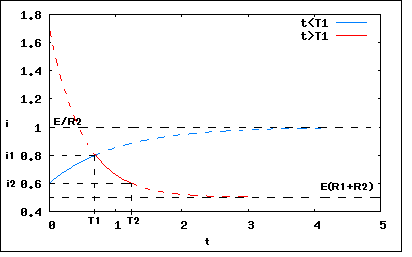 グラフをプロットする関係上もあって、著者とは別解となった。 |
| webadm | 投稿日時: 2011-11-6 1:32 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
もうひとつの:断続部の有るRL直列回路 どんだけあるんだRL直列回路の問題。過渡現象の演習問題は全部で69問あるが前半はRL回路とRC回路で閉められている。
定常状態にある次の回路のスイッチをt=0で開いたとき、R1,R2を流れる電流i1,i2を求め、t=0の前後の様子を図示せよ。 というもの。簡単そうだがどうだろう。 定常状態ではスイッチは閉じているのでR2,Lには電流が流れない。定常電流はE/R1である。 スイッチを開くとLには以前の電流0を保とうとする電圧が急激に発生し電流は0に戻る。そして連続的に時間とともに新しい定常電流E/(R1+R2)にまで増えていく。 というのが予想されるが、それを確認する必要がある。 t=0でスイッチを開いた以降は以下の関係が成り立つ uに関する同次1階微分方程式を解くと ということになる。初期条件としてt=+0でu(0)=Eと置くと ということになる。 従って電流iは ということになる。 電流のグラフとしてはt<0では定常状態であるのでE/R2一定値となり、t>0については上の式の値をとる。E=R1=R2=L=1としてプロットすると 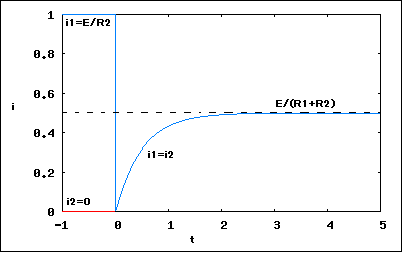 ということになる。 |
| webadm | 投稿日時: 2011-11-6 2:44 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
またしても:RL直列回路 次はRL並列回路の問題かと思ったら問題文を読むとRL直列回路のことだった。
図のようなRL直列回路が定常状態にあるとき、t=0でスイッチを開いたときに流れる電流とそれによって抵抗R1内で消費されるエネルギーを求めよ。 というもの。 スイッチを開いた直後では以下の関係が成り立つ uに関する同次微分方程式を解くと一般解は 初期条件としてスイッチが開かれた直後のt=+0ではそれ以前にLに流れていた電流E/R1は急変せずに流れ続けようとするためu(+0)=E(R1+R2)/R1という電圧がLの両端に発生する(逆起電力とも呼ばれる) ということになる。従って電流iは ということになる。 抵抗R1で消費されるエネルギーは瞬時値電力を積分することで とうことになる。 P.S 結局のところインダクタンスの物理的な性質をわきまえていないと数式だけでは初期条件とかを決めることができない。インダクタンスは弾み車(フライホイール)みたいなもので急には動かないし急には止まらない性質を持っている。 それでは定常状態でLに極めて大電流を流していたとすると、回路を開放したとたん一体何が起こるのであろうか? その予想は読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2011-11-6 6:17 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
鎖交磁束不変の理 次もRL直列回路なんだろうけど2つ並列になっているからそうとも言えない。
図の回路が定常状態にあるものとする。いまt=0でスイッチを開くとき流れる電流を求めよ。 というもの。 ううむこれは今までのように一筋縄ではいかないかも。 既にわかっている条件としては、定常状態での電流である。問題は駆動電源が取り去れれた後にそれらの電流がどう変化するかという点。 物理的にはインダクタンスに流れる電流は不連続的には変化しない。しかしスイッチが開くとL1とL2が互いに電流の流れを阻止するような形で閉回路が構成される。すると電流が今まで通りの値から連続的に変化しようとしてもそうはいかないことになる。 どうすんだこれ(;´Д`) ひとつのアイデアとしては、定常状態でL1,L2に蓄えられているエネルギー量がわかれば、それが開放されてR1,R2で消費されるエネルギーと等しいという関係から積分方程式をたてることができる。それを微分すれば微分方程式になる。なんだそれ(;´Д`) もうひとつは連立微分方程式をたてて解くというもの。重ね合わせでL1,L2どちらか一方しかない場合を考えてどちらも成り立つような解を求める。そのなの習ってないぞ。 これまではLに流れる電流は急激には変化しないと言ってはばからなかったが、どうやらこのケースは例外のようだ。スイッチを開いた直後に残った閉回路に流れる電流はどこで計っても同じになるはずである。とするとL1とL2に流れる電流はスイッチを開く前と不連続となる。 やっぱどうすんだこれ(;´Д`) 手元の電気学会「過渡回路解析」の"8.4 波形の連続性について"を読むと最後にこの問題の回路にあてはまる興味深い示唆が書かれている。 引用:
という理由でほとんどの本ではややこしいことに時間とページを費やしたくないのでこの例外的なケースを華麗にスルーしているわけである。 インダクタンスの磁束とキャパシタの電荷は(インダクタンスの電流とキャパシタの電圧は)不連続には変化しないとだけ習っていると、このケースで矛盾を突きつけられることになる。 手元の尾崎弘「大学課程 電気回路(2)(第3版)」の"3.8 初期値の決定、その他解法に対する注意"に"[1]鎖交磁束不変の理とコイルを含む回路の初期値決定"として以下のことが述べられている 引用:
その後にも重ね合わせの理を使った解法や、これまで何度か出てきた断続部の有る回路を補償定理を使って解く方法が示されている。 鎖交磁束不変の理(principal of constant flux linkages)についてはValkenburgの「Network Analysis」の最初の方のインダクタンスパラメータが最初に登場するところで歴史的経緯を交えて説明されているが、回路系では磁束の総和が不変である意味ということに関してはその後も触れられていない。演習問題にもこの特殊なケースに該当するものが無いことから割愛されていることは明らか。 Valkenburgの「Neetwork Analysis」よりずいぶん後に書かれた(参考文献としてValkenburgの著書が載っている)R.E.SCOTT「Linear Circuit Part1/Time-Domain Analysis」は分厚い本だが、磁束に関しては最初と後の方で二カ所しかない。後の方では一般的なFaradayの法則である磁束の変化と起電力は比例するという関係を述べているにすぎない。磁束の総量については触れていない。 ということで著者の解にもこのあたりは詳しく解説されているので、著者とは違う方法で解くことにしよう。 寝ながら考えたら朝方答えができた(´∀` ) スイッチが開いた直後は以下の関係が成り立つ 従ってuに関する同次微分方程式の一般解は ということになる。ここまでは誰でも一緒。 さて問題は未定係数Kを割り出すための初期条件をどうやって決定するか。 ここで今までのインダクタンスが一つだけの回路の問題を振り返ると、どうやって電源が取り去られた後のインダクタンスに発生する電圧の初期値を決定していたかを思い出そう。 これまではインダクタンスがひとつしか閉回路上に無ければ、それ自身に流れていた電流と不連続が生じないように電流を流そうとする電圧が発生するとしていた。実はこれは答えは同じでも厳密には正しくはないというのが今回判明した。 厳密には、閉回路内のインダクタンスには閉回路内の磁束の総和に不連続が生じないように電流を流そうとする電圧が発生するというのが正しい。この定義によって以前の問題の結果が変わることはない。この現象(自己誘導)を発見したのがHenryでインダクタンスパラメータの単位のHはそこから来ている。 閉回路内にインダクタンスがひとつだけのケースでは、以前にそのインダクタンスが生成していた磁束が電源が取り去さることによって失われることになるので、その磁束に不連続が生じないように電流を長そうとする電圧が瞬時的に発生することになる。 閉回路内にインダクタンスが複数ある場合には、その総量が失われるので、その総和の変化に比例した電圧がインダクタンス全体の和として発生することになる。 と考えればよかったのである。 従って初期条件としてt=+0で閉回路内のL1,L2の磁束の総和が保たれるだけの電流を流そうとする電圧がL1とL2の合計で発生するすればよい。 そこで閉回路内の磁束の総和φ-0はL1とL2の磁束をφ1,φ2とすると、それ以前t=-0に流れていた電流が互いに逆方向なのでその差となる ということになる。t=+0で閉回路を流れる電流をi+0とするとそれによって生じる磁束の総和φ+0は上記と等しいとおくとL1とL2に発生する電圧の総和u+0は ということになる。だいぶ持って余ったやり方だがこれで初期条件が決定したのでuの特別解は ということになる。従って電流iは ということになる。 ちゃんとできたじゃないか(´∀` ) P.S 以前からインダクタンスは弾み車みたいなものと比喩してきたが、このケースをそれで比喩することは出来ない。よく磁束を力学のモーメント(質量と速度の積)と類比させて説明している本を見かけるが、それは単一のインダクタンスに関してであって、このケースのようにある瞬間に2つの別々の向きに励磁されていたコイルが逆向きに接続された閉回路を構成する場合に、力学上でどう比喩すべきか悩んでしまう。互いに逆向きに回転する大きさ(インダクタンス)と(回転速度)の違う弾み車がある瞬間に共通の軸で回ることになったというのとは違う。ちょうど同じ乾電池を2個同じ向きに、1個を逆向きに直列接続した場合に全体では一個分にしか見えないというのも電気の不思議さを物語っている。鎖交磁束不変の理もこれと同じことである。 更に厳密に考えると回路が変化した時点で各素子の両端での電界が急変するのでなんらかのエネルギーが自由空間に放射される(無視できる量かもしれないが、スイッチを開いた瞬間にラジオにノイズが受信されると思われる)。電気回路理論の講義ではそのことは無視しスルーするしかない。 電気の歴史の中では力学との類似な現象が発見されるについれ力学と同じであれば理論的に統一できるという期待が半ばあった。しかしながらそれは別ものであることが次第に明らかになってきた。電気と磁気の性質は座標系によらないが、ニュートン力学は座標権によってその修正されなければならないことも判明した。統一されれば美しいが、現実はそうはうまくいかない。更に新しい視点から見れば、電磁気も力学も重力も、なんだみな同じじゃないか(´∀` )ということになる日もやってくるかもしれない。 |
| webadm | 投稿日時: 2011-11-8 5:08 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続:鎖交磁束不変の理 次もインダクタンスが2つあって、同じ閉回路を構成するように変化する時の過渡現象を解析する問題。
定常状態にある図の回路のスイッチをt=0で開いた。この回路に流れる電流を求めよ。 というもの。 スイッチを開いた以降は以下の関係が成り立つ uに関する同次微分方程式を解くと一般解は ここまでは前問と一緒。 初期条件としてスイッチを開いた直後(t=+0)の鎖交磁束はスイッチを開く直前(t=-0)の鎖交磁束と変わらない(鎖交磁束不変の則)とおくと ということになる。従って特別解は ということになる。従って電流iは ということになる。 式の表記は違うが著者と同一解である。今回はMaximaが珍しく上手に因数分解してくれた。 せっかくだから上の式が著者の解と同値であることを確かめるのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2011-11-8 7:42 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:鎖交磁束不変の理 次の問題もおそらく鎖交磁束不変の理の理解を確かめる問題だと思われる。
図の回路において、t=0のときインダクタンスLに電流i=Iが流れている。いまt=0でスイッチを左側に切り替えて直流電圧E1をIと逆方向に加え、T秒後の電流が-Iになるようにしたい。E1の値をいかに設定すればよいか。 というもの。 単純に与えられたパラメータから過渡現象を解析するだけの問題ではなく、パラメータを意図した動作をするように設計する問題である。 いずれにせよ過渡現象は解析する必要がある。 スイッチが左側に切り替わった時(t=+0)には以下の関係が成り立つ uに関する同次微分方程式を解くと一般解は ということになる。 ここで初期条件としてt=+0で鎖交磁束不変の理により、t=-0の鎖交磁束とt=+0の鎖交磁束は同じとおくと ということになる。従って電流iは ということになる。 ここで問題の題意を忘れると点数がもらえない。t=Tでi=-IとなるためのE1を決定する必要がある。その場合以下が成り立つ必要がある これをE1について解くと ということになる。またしても出たな宿敵双曲線関数(;´Д`) P.S この問題は閉回路中に単一のインダクタンスしかないので、以前やったように回路が変化した直後はそれ以前に流れていた電流Iを維持するための電圧が発生するとしてもよい。 最初の方程式をたてる際にE1の極性を正にしてもやっても構わない。その場合、最終的にE1が逆極性であることが判明する。 |
| webadm | 投稿日時: 2011-11-10 7:26 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
またひとつの:RL直列回路 次もRL直列回路の問題。
理論のときに最初に考えたモデルに立ち戻るような問題。 RL直列回路に図のような周期2T、電圧Eの方形波e(t)を加えた。(2n-1)T≦t≦2nTと2nT≦t≦(2n+1)Tにおける電流iを求めよ。またt=(2n-1)Tとt=2nTにおける電流i2n-1とi2nの比がR,L,Tの値によって定まる一定値になることを示せ。 というもの。ちなみに回路図を描いてみると、左右どちらの表現でも良い。 左はe(t)なる関数で方形波を表したもの。右はスイッチを2Tの周期で交互に切り替えるもの。 いずれにせよ電圧EをRL直列回路に加えて定常状態を待たずに1T後に電圧0を加え(短絡する)、こちらも定常状態を待たずにT後再び電圧Eに戻すを繰り返す。最初の題意は電圧E印可後から取り去るまで、取り去った後から再印可までの電流iを求めよという典型的な過渡現象解析。 題意でわかりずらいのは後の部分で、電圧が瞬時的に切り替わるタイミングでの過渡電流の比がR,L,Tで決まる一定値となることを証明せよというもの。これは電流iが解けていればそれぞれのタイミングでの電流値を求めてその比を計算してみればわかるかもしれない。 まずは電流iを解析するのが先決だ。 といっても以前にあった問題のようには簡単にはいかない気がする。 というのも以前の問題では初期状態が定常状態とその直後の過渡現象を扱うケースがほとんどだったが、この問題ではそうではない。過渡状態が繰り返すことになる。t=∞になれば過渡項は0になって挙動もほぼ同じ現象の繰り返しとなるのだろうが、t=∞になるまで計算するのは無理がある。 なんとか数学的視点から見通しよく最終的な答えを導き出せないものだろうか。工学の主目的はそこにある。 視点を変えてみると、この回路は一種のフィルタ回路である。 二端子対回路として見ると、内部にLがシリーズに一個入っていて、出力端をRで終端したものと考えることができる。Rの両端の出力電圧は回路に流れる電流i=i1=i2に比例すると考えることができる。 あるいはLとRを逆にしてもへそ曲がりだが同じ回路である。この場合、出力を終端するLの両端には電流の微分に比例した電圧が生じることになる。 あるいはもっと単純に見れば出力端を短絡した二端子対回路と見ることも出来る。 しかしこれらは複素周波数を使ったLaplace変換には都合が良いが、結局のところRL直列回路のような一階の常微分方程式のレベルではあまりありがたみがない。これらの考察は複数のエネルギーを蓄積する素子が同じ閉回路に存在する二階の常微分方程式の演習問題で再考しよう。 今朝通勤バスの中でまさに驚くべき解法を見いだした(´∀` ) t=(2n-1)Tとt=2nTに関する電流iの比率を知る必要があるのだから最初に電流iの式を得る必要があるのは確か。しかし1つの式だけで良い。というのもtをパラメータとする電流iの式が解ければどちらのタイミングの値もtを同じ式に代入すれば決定するからである。ということは式は共通の式ひとつあればいいことになる。 ならばわざわざ解を計算で求めずともよいのでは? と思ったけど甘かった。問題を解くには解決の一歩手前が見通しつけばあとはそこへ辿りつくだけのことになるのだが、そこへたどり着く道々に伏兵が潜んでいた(´Д`;) 解決の一歩手前というのは電流iを求める際には一階の非同次微分方程式の解の公式があるのでそれが該当する。伏兵が潜んでいたのは、部分積分を解決するために矩形波の導関数がどうしても必要になってくる。この段階でδ関数とかいう電気回路理論の範疇を超えた概念を持ち出すのは適切ではない。思いついたのはその方法なのだが簡単だけで現時点では封印せざるを得ない。 著者は電気回路理論で使用する数学の帰納法を使って解決の一歩手前までもってきている。くやしいがこれを真似するわけにはいかないのだ。 なんとかややこしい計算抜きで答えにたどり着けないだろうか。 とりあえず途中まで書いてしまおう。 題意のRL直列回路では以下の関係が成り立つ これは一階の非同次常微分方程式なので一般解は公式により ということになる。初期条件としてt=+0でi(+0)=0とすると ということになる。 ここで題意よりe(t)は であるからして。 従ってi2nとi2n-1の比は計算せずとも一目瞭然で ということになる。 著者は途中のi2nとi2n-1の式まではあっているが、最後にその比を求める際に誤りを犯していて、指数が(R/L)Tと正の値で振幅が時間と共に増大する(発散する)という誤った結論になってしまっている。学生の頃に古典で学んだ徒然草の「高名の木登り」を思い出した。 厳密な電流iの式については級数の収束問題を解決する必要があり、見通しの良く示すことが出来なかった。それは読者の課題としよう(´∀` ) P.S 級数の収束問題は最後の式の()内の積分項が収束するかの問題である。もし収束しないとそれに対する四則演算は意味をなさない。幸いなことに電気回路特に受動素子のみから成る線型回路網では一部の例外を除いては電流および電圧は一様収束する(与えられた時間で有界値内の値が一意的に確定する)ことが経験的にわかっているので、それを前提にして議論を進めることも可能である。しかし例外があるので(電圧や電流の値が有界値でなく不確定)その場合には注意が必要である。 著者の様に数学的帰納法を使うのが常套手段だが、それ以外に今まで学んできた数学の範疇では上巻のひずみ波とフーリエ変換で出てきた畳み込み積分なら許容範囲である。 不完全な解答のままで終わるのは忍びないので、畳み込み積分を使って()内の積分項が収束することを示すことにしよう。 と思ったもののよくよく考えたら積分の収束問題は相変わらず残ることに気づいた(;´Д`) この問題はある意味今まで通り過ぎてきた数学の歴史上の問題点に向かい合うことを余儀なくする。何が難しいかというと、電源電圧の関数e(t)が単純な等式で表すのが難しいという点にある。e(t)は有限個の不連続点(t=nTの位置)を持つため連続関数ではないが、不連続点が有限個であればRiemann積分可能である。次に難しいのはe(t)には極限値が存在しない点である。t=∞での極限値を求めようとすると不確定である。これは正弦関数や余弦関数のような超越関数と同じである。かといってFourier級数で簡単に表せるかというとそうではない。そもそも微分方程式の解がいつもy=f(x)みたいな陽関数として表されるとは限らない。この問題はそれに該当するので難しいのだ。 さて問題の難しさが判明した時点で選択肢は2つある、(1)諦める、(2)継続して考える、である。大抵の電気回路本は最初からこの種の難しい問題は華麗にスルーしてしまうので選択の余地すらない。例外的に「詳解電気回路演習」は読者にこの問題で挑戦状を突きつけている。この問題を解くには知恵が必要である。 以前に紹介した「エレガントな問題解決(The Art and Craft of Problem Solving)」には数学的な問題解決方法として、(1)結論の一歩手前の段階を見る、(2)手を動かす、(3)希望的観測、(4)簡単にする、(5)ルールを変える、など視点を柔軟にする方針が紹介されている。それと数学的帰納法、演繹法、変数変換、背理法などの数学テクニックを組み合わせて多くの問題が解けることを例示している。 i2nとi2n-1の比については結論の一歩手前を考えることによってバス通勤途中でアイデアが生まれた。しかしそのやり方は結論としては正しいが数学的には厳密に言うと間違っている。どこが間違っているかというと積分が収束しない限りそれを含む式の値が定まらないのでそれらの四則演算は不定であると言わざるを得ない。この致命的なflawを補う必要がある。それは問題の元来の難しさに立ち戻ることを意味する。 いろいろ検索で調べたり、新しく本を買い求めたりしてみたが、ずばり同じ問題を扱ったものは見あたらない。どの本の著者もこの問題を避けていると言わざるを得ない。ならばなおさら挑戦し甲斐があるというもの。 おそらく19世紀の時代にはこの問題は難問だったと言えよう。ただ一人Oliver Heavisideだけが果敢に挑戦し、正しい結果が得られる当時の数学では証明不能だった演算子法を編み出した。これは数学界への挑戦状ともなり、BromwichがHeavisideから演算子法について詳しく特性を教えてもらい、丹念に数学的に調べ上げて今日知られるラプラス変換と対応することを示した。 この問題の難しさの理由に積分(級数)の一様収束問題をあげたが、これについてWhittaker,Watson「Modern Analysys」を読むと、驚くべきことに脚注に級数の一様収束について理解が曖昧な読者はBromwich「Infinite Series」にあるOsgoodによる図解が理解を助けるだろうと推奨している。この本は出版当時にHardyも絶賛していたこともあって現在も増刷されて手に入れることができる。やはり手にいれて読んでおくべきかもしれない。 様々な困難を伴うこの問題を解決するためには、問題を簡単にするということを試していなかった。問題文そのままで取り組むと難しいが、既に知っていることや解いている問題に近づけるように簡単にすれば何か光が見えてくるかもしれない。 そこで今朝寝床で考えて思いついたのが、重ね合わせの理を使うことに立ち返るということである。そうすると視点が柔軟になり、同じ問題がもっと簡単な問題に見えてくるのが不思議だ。 それは矩形波の電圧源を以下の様に時間と極性の異なる同じステップ関数の線型結合(重ね合わせ)で置き換えることである。これは他には見られないユニークな視点である。 ステップ関数は基本的な過渡現象の最初に必ず登場するし周知のものだ。今回はそれがT時間ずつ時間シフトし、極性が交互に変わる複数(無限数)の電源が直列に接続された等価電源に置き換えることができる。ステップ状の電源電圧変化はこれまで扱ってきたので簡単そうである。あとはそれぞれの電源について解を求めて重ね合わせればできそうである。 他にもFourier級数で表すという方法も考えられるが、実数領域では三角関数の線型結合になり、複素領域では指数関数の線型結合になるのでかなりややこしい。それは読者の課題としよう(´∀` ) (2011/12/23) 大分間が開いてしまったが、その間に考えが問題から離れていたわけではなく、銀行預金が底をつきそうなのでアルバイトの仕事をしたり忙しかったのだ。仕事はやり遂げたが未だ報酬が支払われていない(;´Д`) 川崎駅のLazona内に丸善があるのを知ってそこで面白い微分方程式の本(佐藤光「微分方程式の基礎と応用」サイエンス社)を見つけたのでなけなしのお金を叩いて買って通勤途中のバスの中で読み解いていたり。過渡現象解析の理解には微分方程式に関する達観を必要とすると感じたからだ。この本は比較的ページ数は少ないが、理系で扱う応用問題に取り組めるレベルまで基礎から急勾配斜面を道案内してくれる。特に第三章までの基礎編は必要最小限のものだけを厳選して組まれており、式の誘導には適度のジャンプがあり、そのギャップを埋めるのは良い数学トレーニングになる。理解できない場合には何か基礎的な数学知識や観点が欠けていることを意味するので、それを別途学んだりすることで行間がつながるとしっかりとした理解が構築される仕組みである。おそらく第三章までは著者の長年の大学での講義の結晶であると思われる。 その先の応用については著者自身にとっても筆が進まなかったと序文に告白しているように、道は険しかったと見える。ラプラス変換へ読者を導くためには数学者としてはBromwichが辿ったように複素積分を理解しなければならないというセオリーに基づくのが無理があったのかもしれない。歴史的にはHeavisideの演算子法が先なのだがそれは数学者としてはその存在を認めるわけにはいかない。しかしそうするとLaplace変換の本来の目的、複素積分をほとんど回避して微分方程式が代数的に解く、を初期の段階で見失ってしまう。Heaviside自身はBromwichの仕事(Bromwich積分もしくは逆Laplace変換)の研究に必要な演算子法の知識を惜しみなく提供しつつも自らはBromwichが進める積分法は面倒という結論をとうの昔に出していたと思われる。やはり積分法をつかわずして高階微分方程式が解ける演算子法は当時あまりに先進的であったと言える。 今のところ第4章の複素積分の初歩で躓いていてその先の応用は斜め読みしているだけだけど、高木貞治「解析概論」の後半に出てくる特殊な解析関数(Γ関数、Bessel関数、Beta関数)は元々微分方程式の解と密接な関係があるものだと知った。「解析概論」は微分方程式論は完璧にスルーしている点で問題だと言われている理由がそれでわかった。Bessel関数は昔お世話になった社長さんが数学好きで学生の頃の物理の実験で円盤上に砂を乗せて振動を与えると一定の周波数で模様が現れるという現象を説明するために独自に微分方程式をたてて解いた結果をレポートで出したところ先生にほめられてBessel関数による解とかいろいろ教えてもらったという話しを聞かされたことがある。なるほど物理学と微分方程式はきってもきれない。そういう実験とレポートは学生の中に優れた才能を持つ人を見いだす(逆にアピールする)格好の機会なのかもしれない。と思った。 第4章以降はそれまで無かった誤植(というより明らかに原稿上のミス)が見つかった。著者は単位ステップ関数を式と文章でs(t)とU(t)と混用している。おそらくs(t)はLaplace変換のsと混同するので一般的なU(t)に修正したと思われるが、一部の式や文章で修正前のs(t)が残っていて文章と式とで矛盾が生じる残念な結果となっている。その点を除けば、理論過程のジャンプを読み手が埋める努力をしていけば最短で高度な問題への微分方程式の応用が出来る水準に到達できる良い本である。増版はされているが改訂がまだなのはその評価の高さを物語るのかもしれない。 なんの話しだったけ、ああ、重ね合わせの理を使った別解ね。 難しい問題を解くには「問題を簡単にする」というストラテジーがあるのはもうみんな知っているよね。これは相撲で言えば「自分の相撲を取る」ことは勝利につながるのと一緒。誰も自分の苦手な戦い方をしても勝てる気がしないのと同じ。数学者だったCauerはは、ナチス独裁政権下で数学で飯が食えないと工学分野の仕事で家計を支えた。その際にも苦手な工学の土俵で戦うのではなく、得意の数学の視点から工学の問題を見ることによって見事な成果を次々と生み出した。Fosterのリアクタンス関数(有理形関数)を連分数展開するとLCラダー回路が出来上がるCauerトポロジーや、楕円関数フィルター、線型受動素子回路方程式はすべてAfine変換群をなすという達観など最たるもの。 同じことはできないものの、自分の得意な土俵がどこなのか知っていれば、そこに問題を持っていくのも手である。電気回路理論を学んだのであれば重ね合わせの理を知っているので、線型受動回路であればそれが使える。回路解析は簡単になる。数学をエンジニアリングするという考えかたもある。 そこで先の複数の時間シフトした単位ステップ関数の線型結合(重ね合わせ)で問題の回路の電源を等価に置き換えた場合 という回路イメージとなる。これは以前ひずみ波で学んだ重ね合わせの理で回路を流れる電流が個々の電源単独の時に流れる電流を総和することによって得らることを意味する。 したがって という関係が成り立つ。 それぞれの電源に関する微分方程式の一般解は既に学んだ公式により ということになる。 またt=nTでin(nT)=0と初期条件を置くことによって特解は ということになる。 従ってi0(t),i1(t),i2(t),...とそれらの総和であるi(t)をそれぞれ想定してプロットしてみると、 となることが予想される。 電流は入力の変化によって立ち上がりと立ち下がりを繰り返しE/Rを上限とする範囲内に一様収束する連続関数であることが見て取れる。(n-1)TからnTまでの範囲では正則で、期間T毎に正則でない点を有するが解析接続によって全区間で連続な解析関数とみなせる。 波形は2T周期で繰り返しているように見えるが、厳密には周期関数ではない、すなわち である。 詳しくは先の問題の解答に答える形で議論しよう。 最初に危惧したように前述の重ね合わせの理で合成された電流i(t)が という交代級数で表されるため、級数の発散という疑念を解消しなければならない。プロットからそれが一様収束することが自明だが、この問題は級数の収束という数学の知識を試す意図もあるので、厳密に判定しておくべきだと思われる。 ちなみに上の式でn=0,1,2,3,4についてE=R=L=T=1としてMaximaでプロットし7てみると驚愕の事実が判明 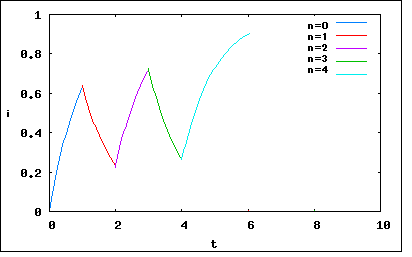 予想外に時間とともに波形が上の方へせり上がっていっていく様子がうかがえる。i(2nT)/i((2n-1)T)は予想通り1より小さいのが確認できる。 級数式を更に整理すると と書き直すことができる。 ついでに手元の回路シミュレータで同じ条件でシミュレートしてみると ほぼMaximaでプロットしたのと同じ結果であることがわかる。 先の級数式からi(2nT)、i((2n-1)T)は ということになる。 従ってi(2nT)とi((2n-1)T)の比は明白で ということになる。 できたじゃないか(´∀` ) 最後に級数が収束するかどうか確かめておこう。 手元にある昭和19年の数学古書、岡田良知「級数論」岩波書店、の"第四章 一般の級数"によれば、 引用:
とある。まさに最後のライプニッツの定理があてはまる。 従って級数は収束するので、それを含む四則演算が成立し結果は正しいということになる。 ふう、ながったよママン(ノД`) |
| webadm | 投稿日時: 2011-12-29 5:39 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RL直並列回路 次の問題はRL直列並列回路に関するもの
上のようなRL直並列回路において、t=0でスイッチを閉じて直流電圧Eを加えるとき、抵抗R1,R2,R3を流れる電流i1,i2,i3を求めよ。 というもの。 ストラテジーとしてはいくつかあり ・i1,i2,i3に関する連立微分方程式をたててそれを解く ・L1,L2,L3の電圧降下をu1,u2,u3として連立方程式をたてそれを解く ・i1に関して駆動点から見て回路全体の合成抵抗Rと合成インダクタンスLのRL直列回路に関する微分方程式を解く、また同様にi3に関して出力端から見た等価電圧源と内部インピーダンス(R0とL0)のRL直列回路に関する微分方程式を解く、残るi2はi1=i2+i3の関係から導く というものが考えられる。単純に連立方程式をたてて解くやりかたは既に著者が示しているので、それとは別の方法でやってみよう。 あまのじゃくだけど、RL直並列回路をもっと簡単なRL直列回路の問題にする最後のアプローチに挑戦してみよう。少なくとも問題は簡単になるはずだ。 上の2つの閉回路について微分方程式をとけばよいのだが、もっと簡単にするために、下記のように2つのRL直列回路の問題として考える。 i1に関しては入力電源から見て回路の駆動点インピーダンスは合成抵抗Rと合成インダクタンスLの直列回路と等価に見えるはずである。 またi3については等価電圧源回路に置き換えることによって、出力インピーダンス(R0とL0)と等価電圧源E0・U(t)のRL直列回路にほかならない。 i1とi3がわかればi2はその差分であるので自動的に決まる。 これならば既に交流回路で学んだ方法が使え、RL直列回路に関する微分方程式だけを解けばよいので見通しが良い。 i1,i2,i3の定常電流は定常解析により定まるのでだいたいの過渡応答の予想がつく。線型素子回路ではいずれにしても指数関数の線型結合となることが判っているからである。ちょっとずるいかもしれないが、工学的な視点ではそういった予測は解の一歩手前を考えるのに重要である。 へそまがりなアプローチをやってみると、王道的なアプローチからは死角になって見えないでいたいろいろな理論の側面を発見することができる。 最初に複雑な回路を2つの一端子対回路と電源の閉回路の問題として考えるアイデアは突飛でもないものだが、いきなりそこに躓きの石があることに遭遇する。 駆動点から見て等価な一端子対回路という考え方は悪くなかったが、それが等価なRL直列回路になるという仮定がまずかった。以前学んだ定常解析の手法で駆動点インピーダンスの式は ということになる。これは複素周波数sの有理形関数である。s=jωを代入すれば交流回路理論で学んだおなじみのインピーダンスの式になる。s=σ+jωを代入するとそれは次に学ぶLaplace変換によって複素周波数領域に変換された電圧入力に対する電流出力の伝達関数である。これに同様に電圧入力関数をLaplace変換して複素周波数領域の関数として乗じれば、結果は複素周波数領域の電流出力関数となる。それを時間領域に逆変換すれば時間領域での解が得られるというもの。しかしここではLaplace変換はまだ使わない。 定常解析は周波数領域の解析であるためそのままでは時間領域の結果を導くことにはならない。頭の良い人から見れば、「そんなの最初から判っているじゃん、普通しないよ、ばーかばーか」と言われるのがおちである。 しかし面倒な微分方程式の解法を避けてこの裏道に迷い込んで見ると、ふとHeavisideが横を通り過ぎて先へ進んでいったような不思議な感覚を覚える。彼もかつてここを通っていったのではないだろうか。現代的に考えれば、周波数領域と時間領域とでは基底が異なるだけで同一の回路の写像である。周波数領域で同じ特性を持つ回路は時間領域でも同じ過渡応答をする。なぜならどちらも同じ回路なのだから(´∀` )そう考えれば、周波数領域の結果と時間領域での結果は互いに一対一の写像関係が存在するということが確信できる。19世紀にはこれはまだ証明されていなかったが、Heavisideはこのことを確信していたに違いない。それは間違ったアプローチだった結果は正しかった。 その話しとは別に上の複素有理形関数を第一Cauer(連分数)展開してみると ということになる。つまり回路的には と等価ということになる。元々6素子だったのが、4素子に減っている。 どうしてこうなるのだろうか?4素子に展開された複素インピーダンス関数の式ににそれぞれ素子定数の式を代入してみれば元の有理形関数の式になることで等価であることが確認できる。良く考えればL1と直列だったR1は並列回路内に含めてしまうことができる。また並列回路部分も鎖交磁束不変の理からすれば閉回路内のインダクタンスはひとつあれば済むことになる。 元々多項式は任意の基底を選ぶことによって幾通りにも表すことができる。最も都合の良い多項式を表す標準基底(Hironaka's standard basis)というのが局所環上に存在することは日本の数学者広中平祐が特異点消失理論の際に証明していたが、実際にそれを多項式環上で求める最初のアルゴリズムが近年になってオーストリアの大学院生ブッフバーガー(Buchberger)によって発見された。グレブナー(Gröbner)指導教授に敬意を表すためブッフバーガーのアルゴリズムで求められる基底はグレブナー基底(Gröbner basis)と名づけられた。こちらが昨今は有名である。Maximaにもグレブナー基底を求める機能が実装されている。 受動素子のみから成る回路も同じで、まったく同じ極と零点を持つのであればそれは素子構成が異なってもそれらは全て等価な回路である(物理的な構成方法は異なっているが)。これなどは標準的な抵抗やコンデンサが標準数の数列に基づいた素子定数のものしか一般には販売されていないので、必要な素子定数の素子を複数の素子を組み合わせて構成するのはよく行われることだ。実際それが可能だ。単純な回路であっても素子定数が標準で用意されているものと大きく異なる場合には、標準の素子定数のものを複数組み合わせて等価な回路を構成するしかない。通所これらは機械的にはできないので、設計者が試行錯誤しながら構成や素子を選定することになる。近年発見された代数幾何学のアルゴリズムを使えばこれらもコンピュータプログラムで出来るのかもしれない。あるいはもう実用化されているのかもしれない。 単純に見える6素子のRL直並列回路だが、たかが駆動点インピーダンス関数だけを見ても複数のイデアルの加減乗除からなる係数を持つ多項式から成ることが見てとれる。Maximaでは式の複雑さが扱える限界に近い。 そんな普段は目にすることがない電気回路理論の側面を見ることができたりするのも脇道にそれたおかげである。 さて話しを元にもどそう。複素周波数領域で見ると駆動点インピーダンス関数はもっと少ない素子数で構成される回路と等価であることが判明した。同時に単純にはRL直列回路にはならないということも。駆動点インピーダンス関数が抵抗(R)とリアクタンス(X)で表せるというのとRL直列回路になるというのを勘違いしていたのは大失敗だった。いずれにせよその抵抗RもリアクタンスXも周波数の関数であるので、そのまま時間領域で使うことはできない。 どうすんだこれ(;´Д`) これだと回路が簡略化されたものの素子定数はめちゃめちゃ複雑なので、元の6素子回路で計算したほうが簡単な気がする。一端子対回路として考えるアプローチには変わらない。 ちなみに前述の式を第二Cauer展開してみると、素子数は同じ4素子だが直列部と並列部が異なる構成の回路になることが確認できる。直列部はRのみとなり、並列部は片方がLのみ残りがRL直列回路というもの。これは直列部のL成分が並列回路に移動したとものと考えることができる。 いずれにせよ、この問題を解くには連立一階微分方程式を解かねばならないのは明らかである。演算子法やLaplace変換を用いない限り。 (2012/1/1) ふう、給湯器が復活したので数ヶ月ぶりで湯船につかり全身の骨髄に溜まった疲れが滾々と湧き出てしばらく寝てしまった。 もう少し脇道にそれた議論をしてみよう。 前出の複素周波数による駆動点インピーダンス関数はその零点と極によってその特性がきまるのは以前一端子対回路で学んだ通り。先の駆動点インピーダンス関数の零点は有理形関数の分子の式が0となるsを求めればよく ということになる。受動素子のみからなる一端子対回路のインピーダンス関数は正実関数なので、その零点と極は常にs平面の左半面にのみ存在することになる。インピーダンス関数の零点は回路的にどういう意味を持つのだろうか? 既に知っている単純なRL直列回路について複素周波数領域での零点を求めると ということだった。これは過渡応答の際の時定数そのものである。つまり複素周波数領域の零点の実部が時間領域での時定数に一対一で対応すると仮定すれば、解析が簡単な複素周波数領域での特異点を知れば時間領域での解も自ずときまるのではないかという予想がたてられる。 問題のRL直並列回路は受動素子のみからなるので駆動点インピーダンス関数は正実関数となり、常にb^2≧4acの関係が成り立つと考えて良いことになる。 このことを頭に入れて駆動点に流れる電流i1(t)を求めてみることにしよう。 回路を流れるi1,i2,i3のうち線型独立なのはその2つのみなので、閉回路電流i1,i3についてのみ考えればよいことになる。以下の関係が成り立つ (2012/1/3)微分方程式の誤りを訂正 これを見通し良くするために線型代数の行列表記に書き直すと ということになる。これは定係数線型非同次2元連立一階微分方程式のベクトル表記ということになる。 どうすんだこっから(;´Д`) 既に理論の時にRCL直列回路の解析で定係数線型同時二階微分方程式が登場した際に同じように線型代数のベクトル表記を用いた。あのときには一階と二階の導関数をそれぞれ線型独立な未知関数として連立微分方程式に書き直して解いたのだがそれと基本的には同じである。 一階の微分方程式であることには代わらないので、i1かi3に関する微分方程式が得られれば既に学んだ定係数非同次一階微分方程式の解法手順を使って解くことができる。問題は前述の方程式のままではi1とi3が混じり合っているのでそれを分解しないといけない点である。 解法のアプローチとしては2つあり、 ・オーソドックスな微分方程式の解法を用いる ・モダンな線型代数学を用いる 第一のアプローチは既に著者が一例を示しているが、一端1変数微分方程式に分離できれば一階微分方程式の解法が使えるのでこれは説明するまでもない。 第二のアプローチは予め線型代数の知識が無いとつらいが、近年の微分方程式論の本には必ず取り上げられておりむしろこちらが今後は有用である。こちらのアプローチで行ってみよう。 最初にまず以下の同次微分方程式で解を求める必要がある。非同次微分方程式の一般解は同次微分方程式の解を含んでいるからである。 未知のベクトルxが未知の関数の拡張と見なすと、これの一般解は既に知っている という形になっていると予想される。しかし問題は行列Aを指数とする指数関数という新たな概念が必要になってくるという点である。実は歴史的には線型代数のスペクトル分解や固有値問題も連立微分方程式の解法問題が発端である。なので先に線型代数を学んでも微分方程式のここの話しを知らないと単なる教養ということになってしまう。 この議論を扱っている数学書はさっさと線型代数の成果を使って先へ進んでしまうのだが、ここでは少し寄り道をすることにしよう。 上のベクトル表記の解が問題の同次一階微分方程式の解であると仮定すれば、解の式を同次部分方程式に代入してみると が成り立つので確かに解である。ここまでに勝手に行列Aを指数にもつ指数関数が体kの元を指数にもつ指数関数の拡張であると見なして議論を進めてきたが、具体的な解を得るには厳密に定義する必要がある。 その前にベクトル表記の同次微分方程式を独立した2つの変数分離形に分離できないだろうか?そうすれば積分するだけで解が得られる。 これにはやはり線型代数の行列の対角化もしくは標準化、あるいはスペクトル分解と呼ばれる定理を使用する。行列Aに関して以下の関係が成り立つ正則行列Pが存在すると仮定する ここでp1,p2は互いに線型独立なベクトルである。この正則行列Pを用いて元のベクトル表記の同次微分方程式を変数変換と行列の性質を使って巧妙に書き換えると ということになる。これでようやくy1とy2に関する独立した同次一階微分方程式が得られるのであとは変数分離して両辺を積分すると ということになる。 なんだ簡単じゃないか(´∀` ) だがしかしこっから先が見通しが真っ暗(;´Д`) 行列の固有値はいいのだけど、固有ベクトルがわかんね。 予想によるとi1の解の時定数は駆動点インピーダンスの零点の実数部になるはずだからmaximaでインピーダンス関数の分子の式の零点を求めると ということになる。Maximaで得られる式はfactorが不完全なので一部手でfactorしてあるが等価な式である。著者の解にある特定方程式の根とも一致している。 しかしこちらが建てた方程式の係数行列Aの固有値を求めると上の零点の式と違うのだ。何か決定的な誤りがあるのだろうか? (2012/1/3)決定的な式の誤りを見つけた(;´Д`) どうもR1があまりに関与してないと思ったら最初に建てた式を整理したところでR1の項がひとつ落としてしまっていた。それで係数行列Aの内容が誤ったものになり固有値が違ってしまっていたのだ。 これでもう大丈夫だ。 係数行列Aの固有値を導くと ということになる。これは既に承知の駆動点インピーダンスの零点と同値である。 次にそれぞれの固有値に関する固有ベクトルを導くと 従って同次微分方程式の一般解は ということになる。 次にいよいよ最終的な非同次微分方程式の解を導くことになる。 X(t)を同次微分方程式の基本行列、u(t)を未知のベクトル関数としてx*(t)=X(t)u(t)が非同次微分方程式の解を表すとすると ということになる。この形はどっかで見覚えがあるな。 具体的に計算してみると だめだ('A`)マンドクセ どうすんだこれ(;´Д`) 最初に出てきた行列を指数にもつ指数関数を考えてみよう。 係数行列の固有値が相異なる2つの実数λ1,λ2を持つケースで以下が成り立つ射影行列P1,P2が存在する 射影行列には以下の面白い性質がある つまり相異なる射影行列の和は単位行列となり、自分自身をべき乗しても変わらないが、相異なる射影行列の積はゼロ行列となる。これは行列を指数にもつ指数関数の展開時に大変都合が良い。 問題の係数行列Aの射影行列を計算してみると ということになる。 ここで行列の指数関数は射影行列を用いて ということになる。これも見覚えがある。 これが同次微分方程式の基本解ということになるので、非同次微分方程式の一般解は定数変化法によって ということになる。なんだみんな同じじゃないか(´∀` ) 今度こそ計算できるかな。 だめだ('A`)マンドクセ 結局Maximaで扱えないぐらい複雑な多項式になってしまうので手作業でトリッキーな式の因数分解をしないと手に負えないことがわかった。 あとはいいところまで行った同次微分方程式の一般解の不定定数項を初期条件t=+0を与えて割り出してみよう。 だめだc1,c2を解いても式が複雑すぎて以降扱いきれなくなる。 どうすんだこれ(;´Д`) 実はMaximaには連立微分方程式を解く機能が備わっているらしい。しかしほとんどだめぽい。駄目もとで試してみたら一応解けた(;´Д`) e1:L[1]*diff(i[1](t),t,1)+R[1]*i[1](t)+L[2]*(diff(i[1](t),t,1)-diff(i[3](t),t,1))+R[2]*(i[1](t)-i[3](t))=E e2:L[2]*(diff(i[1](t),t,1)-diff(i[3](t),t,1))+R[2]*(i[1](t)-i[3](t))-L[3]*diff(i[3](t),t,1)-R[3]*i[3](t)=0 desolve([e1,e2],[i[1](t),i[3](t)]) しかし式があまりにここに載せるには長すぎる。手操作で置換整理したところだいたいあってそうだがsinhの項だけうまい因数分解が見つからない。 Maximaなかなかやるじゃないか( ̄ー ̄) 自分で計算するとどれも正解に到達しそうに見えなかったのに。 実はこの問題の回路を手元の回路シミュレーターでシミュレーションしようとしたところ意図した通りにいかなかった。原因はどの経路もインダクタンスが直列に接続されている点にある。インダクタンスに限らずキャパシタンスも同じだた同一の閉回路中に複数のリアクタンス素子があると困るらしい。初期状態でインダクタンスはショート状態とすると一応シミュレーションできるが、初期電流0だと怒られてシミュレーションしてくれない。確かに2つのリアクタンス素子が直列になっていると、その電圧降下は不定である。しかも初期電流が0とあればなおさらである。つまり2つのリアクタンス素子が直列に接続されていた場合、その中点の電圧はどうやって計算するかという問題である。電流が流れないと電圧が発生しないのだからやっかいだ。 L1のみ初期短絡という設定にしてシミュレーションした結果は以下の通り i1がi2とi3の和になっているのが見て取れる。RL直並列回路は一般的にβ≧0となりRLC直列回路のような振動は発生しない。これは零点が負の実軸上にある限りそうである。もちろんL1,L2,L3のいずれかが負のインダクタンスとかであればその限りではない。 実際にはシミュレーションで使用した素子定数(R1=1,L1=1,R2=2,L2=2,R3=5,L3=5)だとちょうどβ=0となり臨界減衰の特性を示す。驚いたことに著者の解はこの条件を除外している。β=0の場合は特性方程式の根が重根となるので、解も異なってくるのだ。シミュレータでうまくいったので、Maximaでプロットしようとしたら0による除算が発生して計算できない(;´Д`) 著者の解もβ>0のケースのみに限定している。実際には適当に選択した上のような素子定数でβ=0となってしまうのだった。 しかたないので、R1を0.99にちょっとずらしてβ≠0となるようにしてプロットしてみた。 これは著者の式に基づいてプロットしたものなので、当然ながらシミュレーション結果とよく一致している。 Maximaで上と同じ素子定数で先ほどたてた連立微分方程式を解くと、素子定数が確定しているので係数がすべて数値となった解が得られる。これを同様にプロットすると というわけでMaximaで解いた結果はあっているということになる。どうやったら式が綺麗に整理されるやら。 先の途中まで整理した式で同じようにプロットしてみたら、似てもにつかぬ波形になりましたとさ(;´Д`) 先ほどのdesolveで得られる式を整理したものではなく、定数だけを数値に置き換えていった式だとちゃんと期待通りの結果が得られるので、どっかで式の整理を間違えたということに。 微分方程式の本でも代数的関数的に微分方程式を解いている例を示しているのは一般解までで、例題とかでは定数はすべて実数値で与えられているので計算がそれほど面倒なことにはならない。たかが6素子の回路でも係数の多項式はありとあらゆる要素の加減算とべき根が出現してわけがわからなくなる。とても頭に記憶して暗算で式を整理などは無理がある。紙の上でも間違いが多発してどうにもならない。 そんな事情は数学者の関知するところではないので、19世紀にはいって微分方程式論は非線形方程式の解の存在に関する問題の方が重要で実際問題計算などどうでもよかったのだ。やはりHeavisideの演算子法の登場は技術者にとっては朗報であったことは明らかである。なにしろ微分方程式論は方程式をたてることができる程度知っていればよく、それ以外は代数的な式の操作に関する知識以外は必要ないのだ。 この問題は試験にでたら、解答を暗記でもしてないかぎり落とすしかないかもしれない。最終解に到達するのにとても時間がかかるし完全に答えるには臨界減衰(β=0)と過減衰(β>0)の2つのケースについて解く必要がある。「時間ねー」という事態に陥るのは必至である。 でも半分ぐらいまでやったら半分ぐらい点をもらいたいぐらいだよね(;´Д`) ということでこの問題は中途半端なところで一端終止符を打つことにしよう。いつも完璧というわけにはいかない。 間違いに気づいたら、後日訂正するかもしれない。 自信のある読者は自ら別解を試みられるとよい(´∀` ) P.S 著者の解の式は過減衰(指数関数項が複数)のケースだが、Maximaで解いた結果は臨界減衰となっている(指数関数項がひとつ)が見た目上は区別がつかない。ほとんど臨界に近い過減衰だからだろうか。 しかしシミュレータが無かった昔の人の苦労が忍ばれる問題であった。今ならこれ以上難しい問題を机上で解析するというのは誰もやりたがらないかも。しかし解析をやらないと素子定数が一意的に決定できないという逆問題がある。どこが特性に敏感な素子なのかも予め予測できていないと試行錯誤では設計が終わらない。 P.S "The Art and Craft of Problem Solving"に"問題が難しすぎるなら、簡単な問題を解くとよい”と書いてあったのを思いだして、行列の要素が式だと難しいので予め素子定数値を代入してどの数学書の演習問題にあるように数値行列にしてみたら解の姿が良く見えるのではないかと夕食後に微分方程式をたてるところから始めて実際に以下の数値を代入してみた L1=2,L2=2,L3=5,R1=1,R2=2,R3=5,E=1 すると驚愕の事実が判明した。 なんと適当に標準数列から順番に選んだ素子定数によって係数行列は綺麗に対角化されてしまうという事実が判明した。偶然なのか出題者が暗に意図していたのかは謎。これによって非同次一階線型連立微分方程式は独立した2つの非同次線型一階微分方程式に分離されることになる。 これは簡単すぎて暗算でも解ける。公式によりそれぞれの非同次微分方程式の一般解は 初期条件としてt=0でi1=0,i3=0を与えると特定解は ということになる。従ってi2は ということになる。 これらはシミュレーションやMaximaでのプロットとよく一致する。 ということでアプローチは間違っていないが、係数を記号式のままにするとたちどころに扱い難い代物になってしまうのが敗因だった。 それにしてもまったくうまいこと係数行列が単位行列になってしまう瞬間を目の当たりにしたときは感動した。出題者がこの問題に込めた秘密の暗号を見つけたような気分である。 数式を処理するのが面倒なら最初に適当に数値を代入して数値行列にしてしまうと結論が見えて良いかもしれない。 |
| webadm | 投稿日時: 2012-1-11 8:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
相互誘導回路 次の問題は久々に登場する相互誘導回路の過渡現象解析
以下のような相互誘導回路で、t=0で一次側のスイッチSを閉じて直流電圧Eを加えるとき、開放されている二次側に誘起される最大電圧を求めよというもの。 最後に相互誘導回路の問題をやったのは上巻のどこだったか。もう詳しいことは忘れてしまった。微分方程式をたてるためには相互誘導回路を数式モデルにしないといけない。幸いなことに等価回路だけは記憶に残っていた。それを使うと以下のように考えることができる。 これならば微分方程式は簡単にたてられるだろう。2つの閉回路(といっても二次側はオープンなので閉回路と言えるかどうかは疑問だが、電流0流れている閉回路と考える)について以下の関係が成り立つ ここでi2=0であるのでdi2/dt=0となり ということになる。第一の式はi1に関する定係数形非同次一階微分方程式ということになる。これは公式によってi1の一般解は ということになる。初期条件としてt=0でi1=0を与えれば ということになる。 一方二次側の開放端電圧e2は ということになる。従ってe2はt=0において最大値をとり ということになる。 |
| « 1 (2) 3 4 5 ... 7 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

