| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2012-1-11 10:52 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続:相互誘導回路 次も相互誘導回路の問題
以下の回路におけるインダクタンスL1に直流電流I0が流れているとき、t=0でスイッチを閉じれば各回路にどのような電流が流れるか示せというもの。 これも以下の等価回路で考えてみることにする。 2つの閉回路に関して以下の連立微分方程式が成り立つ これを線型代数のベクトルで表すと ということになる。 係数行列Aの固有値は ということになる。従って同次微分方程式の一般解は射影行列を使用して ということになる。 従って非同次微分方程式の一般解は上記の基本解を用いて ここでt=0の時にi1=I0,i2=0なる初期条件を与えると各電流は ということになる。 もってまわった解き方だけど、線型代数と連立微分方程式を用いて解くという別解を示したかっただけだ。物理学や工学では線型代数と連立微分方程式は重要かつ不可欠になるので一緒に学ぶとよい。というか線型代数だけ学んでもなんのことやらさっぱり頭に入らないけど、連立微分方程式と一緒に学ぶとそういうことだったのかと問題の発端がわかるのである。 P.S よく見るとi2の解が不可解である。t→∞でi2→M*I0/L2となってしまう。電源が取り去られた後も電流が永遠に流れ続けるというのはあり得ない。著者の解も同じ結果だったので安心していたが、どっか間違ってないか? 試しにMaximaで問題の連立微分方程式を解かせてみると、やっぱり同じ結果が得られる(;´Д`) どうなってるんだ。誰も疑問に思わないのかこれ? でもよく考えたらこれで正解なのかもしれない。というのも二次側の閉回路には抵抗が含まれていないのでエネルギーを消費しない。つまりL2とそれを含む閉回路が電気抵抗がゼロの超伝導体でできているとすれば起こり得ることである。 電気回路理論に出てくるインダクタンスは理想インダクタンスなので内部抵抗はゼロである。つまり超伝導体で出来ていると考えてよいし、配線も抵抗器を除いては超伝導体でつながっているとみなしてよい。 そういえば永久磁石なんていうのも、一度電磁誘導で磁性をもたせるとそのまま磁力を保持するというのも不思議だよね。原子か分子レベルで電流がループ状に永久に流れているとでも考えないと説明がつかない。 Faradayは最初電磁誘導の実験をする際に予め直感で二次側に電流が流れ続けることを予想していたが観測事実はそれを否定するものだった。その代わりそれまで知られていない相互誘導現象を確認できた。しかしFaradayの時代にもしも超伝導材料があったら、話しは違っていたかもしれない。Faradayの最初の予想が実は正しかったのだ(´∀` ) |
| webadm | 投稿日時: 2012-1-14 21:44 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:相互誘導回路 次も相互誘導回路の問題。前問では二次側の閉回路で電力が消費されない特殊なものだったが、今度は実験室で再現できる二次側でも電力が消費されるもの。
以下の回路のスイッチをt=0で閉じた。一次側と二次側の電流を導けというもの。 これも以下の等価回路で考えることにしよう。 t>0で以下の関係が成り立つ これを例によってベクトルで表すと ということになる。従って同次微分方程式の基本解を求めるために係数行列Aから固有値を求めると ということになる。従って定係数形連立非同次微分方程式の一般解は係数行列の指数関数を用いた公式により ここで初期条件を予めt=0でi1=i2=0を与えると不定積分項は定積分に置き換わり未定ベクトルcは初期条件となり特解は ということになる。行列の指数関数は前問と同様に射影行列の性質を用いて導くことが出来る。固有値は2つの異なる実数であることから ということになる。 計算を簡単にするために解の式を畳み込み積分の形に書き換えると ということになる。おろ著者の解答とは似てもにつかない。 しかしこれはMaximaで解いた結果と一致している。怪しいのは著者の解だということになる。ちなみに著者の解を元の微分方程式に代入してみると解ではないことがわかる。著者がどこでどう間違ったのかを見いだすのは容易ではない。それを見つけるのは読者の課題としよう(´∀` ) Faradayが実験した時もこれと同じ回路だった。λ1,λ2とも負の実数なのでt→∞でi1,i2は0となる。これはFaradayの期待とは反したが相互誘導作用があることだけは確かめることができた。同時期にHenryも相互誘導と自己誘導の発見をしたが発表が遅かったので相互誘導の発見者はFaradayとなった。Faradayは数学的な専門知識を持ってなかったので、後にMaxwellが補うことになる。 E=R1=L1=1,L2=R2=M=1としてプロットしてみると 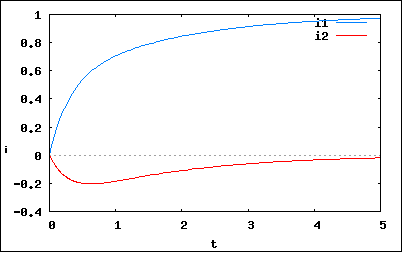 ということになる。この考察も読者の課題としよう(´∀` ) Maximaを使うと手で解くのがばからしいぐらいに簡単に連立微分方程式が解けてしまう。実はここまで到るのにさんざんな苦労をした。以前の問題では記号式をむやみに展開してしまって処理しきれなくなったので、今回はなるべく展開しないようにやり直したところ線型代数の性質で簡単に式が導出できることを発見した。これはちょっとオリジナル性が高いかもしれない。 やはりこれからは線型代数だろう。 P.S 通勤途中で道々考えていたら、行列の指数関数を積分するのではなく、それを展開した後に積分するアプローチがあることに気づいた。すなわち なんだか疲れてきたのでこれ以降は読者の課題としよう(;´Д`) そのかわりといってはなんだけど、Heavisideが現代に蘇ったならこの問題を以下の様に簡単に解いてしまうだろう。 Heavisideの抵抗オペレータ(演算子)で最初の連立微分方程式を書き直すと ということになる。すなわち抵抗演算子行列Fの逆演算子行列F^-1を両辺に乗じれば ということになる。もし抵抗演算子Fに対する逆演算子F^-1が一意的に決まるなら解がたちどころに得られることになる。このことはHeaviside没後20世紀になってHilbert空間での線形作用素論として裏付けがなされた。その先見性を評価したドイツのGöttingen大学はHeavisideに名誉博士号を贈与している。欧米では作用素はOperatorであり演算子と同じ意味のものであるが、日本の数学界では区別するために作用素と名付けている。物理数学では依然として演算子と呼ばれている。 では実際に逆演算子を求めてみよう。まずは演算子行列の逆行列を計算するとこれは簡単に 逆演算子に変換するにはpに関する部分分数に展開し 1/(p-a)を対応表から(1/a)(exp(at)-1)に置き換えれば逆演算子行列は ということになる。従って解は ということになる。積分計算なしに解が代数操作でいとも簡単に得られてしまった。やはり驚くべき洞察ということにつきる。 ここで気がつくのは、演算子法の場合初期問題を考慮するステップが無いという点。例えばt<0でスイッチがONでt=0でスイッチがOFFする初期条件の解を求める場合には更にステップが必要である。そうした注意点を除けば、電気回路や線型システムの工学問題は簡単に解が得られてしまうのだから、物理や工学の分野では驚きを持って歓迎されたのは言うまでもない。Cambridgeの数学者だけが嘲笑しただけだった。「傲慢は知識の妨げである」というのはイギリスの詩人Byronの名言である。Byronの娘AdaはBabbageの解析機関開発資金を公募するためにすばらしいプレゼンテーションを行った、世界で最初の女性プログラマとも言われているが、むしろ解析機関開発ベンチャーのCEOだったと言える。 なんの話しだったっけ、ああ演算子法ね。 これほど苦労して解にたどり着けない隘路がいくつも潜んでいる連立微分方程式だけど、演算子法を使うと見通しよく解に最短で辿りつけることは驚愕の事実である。それが実感できるのは19世紀の数学水準で同じ問題を解いてみないとわからない。Heavisideの演算子法はベクトル解析に通じ、多次元の微分方程式を見通しよく解くために必要な共通の概念に基づいていると言える。 P.S 今時Heavisideの演算子法を使っても歓迎はされないだろう。戦後になって演算子法は欧米諸国ですべてLaplace変換に差し替えられてしまったので今日教科書にも出てこない。しかしそれではLaplace変換の有難味が良く伝わらないのではないだろうか?演算子法が最初に提供した微分方程式のシステマティックな解法という驚きを追体験することは依然として価値があると思うからである。 個人的には演算子法について「演算子法と其応用」和田重暢 著、「第一級無線技士用 電気回路(下巻)」室住熊三 著それに共立「数学公式 改訂増補 附関数表」で学んだ。これらのいずれも、非同次微分方程式の右辺には単位ステップ関数(Heaviside関数)の積であることを忘れないようにその旨式にも太字で"1"と書かれている。これまでの演習問題でも右辺に定数が現れる非同次微分方程式には単位ステップ関数であるU(t)を記載するようにしてきたが、以降は書かれているものとして省略することにする。必要な場合には再度記載するようにするつもりである。 実のところ非同次微分方程式では右辺が関数であるのが一般的なので、定数というのは厳密には正しくない。定数x単位ステップ関数が正しい。この意味は理解が有る程度進まないとわからないかもしれない。むしろ過去無限大の時間から定数というのは積分が無限大になるので都合が悪い。 ということで今後右辺に定数ベクトルが現れた場合には、定数・U(t)の意味で解釈して欲しい。 |
| webadm | 投稿日時: 2012-1-22 3:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
まだまだ:相互誘導回路 次もRL直並列回路の問題
以下の回路において、t=0でスイッチを閉じるとき、一次側、二次側を流れる電流を求めよ。ただしL1L2≠M^2とする。 というもの。これも以下の等価回路で考えてみよう。 t>0で以下の関係が成り立つ これをMaximaで解くと と解ける。ちゃんと著者の解と同様に双曲線関数を使った表現になっている。 以下の様に連立微分方程式をたてても同じ結果が得られる これだけではさすがに答案にならないのでHeavisideの抵抗オペレータを使って上記の回路方程式を書き直すと ということになる。従って解は演算子法を使って導くと ということになる。これを更に整理すると ということになる。著者の解と同じ様に変形するのが大変だった。解自身は演算子法を使用することで積分計算を一切せずに得られている。 E=L1=R1=M=1,L2=R2=2としてプロットしてみると 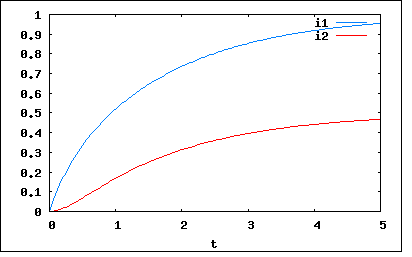 ということになる。i2の立ち上がり部分に注目すると異なる時定数(1/λ1,1/λ2)もつ指数関数の合成(線型結合)であることがわかる。 演算子法があまりに最強すぎて問題がぬるぽに見える(´∀` ) |
| webadm | 投稿日時: 2012-1-22 23:50 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RC直列回路 今度はRC直列回路の過渡現象解析問題
以下のRC直列回路において、t=0でスイッチを閉じて直流電圧Eを加えるとき、流れる電流iおよび電荷qを求めこれを図示せよ。また任意の時間T1における電流の接線が定常電流I=0と交わる時間をT2とするとき、その差τT2-T1は時刻T1に関係なく常にRCとなることを証明せよ。さらにt=0では電圧Eは抵抗のみに加わりキャパシタンスには加わらないことを示せ。ただし、t=0におけるキャパシタンスの初期電荷は0とする。 電流iと電荷qに関して以下の関係が成り立つ これをHeavisideの抵抗オペレータを使って書き換えると ということになる。pは微分演算子、1/pはp^-1で積分演算子。 従って演算子法で解を導くと ということになる。p/(p+a),1/(p+a)は変換表によりそれぞれexp(-at),(1/a)(1-exp(-a))へと変換した。 i,qをそれぞれE=C=R=1とおいてMaximaでプロットしてみると 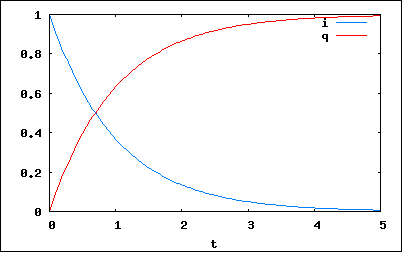 ということになる。 3つめの題意が難しいかもしれない。 任意の時刻T1における電流の接線の傾きは電流の導関数から 従って接線がT2で時間軸と交わる条件よりτは ということになる。 t=0でのCの電荷は0である題意で与えられているのでt=0におけるCによる電圧降下は0となり、電源電圧Eはすべて抵抗に加わることになる。 |
| webadm | 投稿日時: 2012-1-23 1:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続:RC直列回路 次は前問の続きのような問題
RC直列回路にt=0で直流電圧Eを加えた。抵抗RとキャパシタンスCの端子電圧eR,eCが等しくなる時刻Tは時定数τ=RCのみに依存することを確かめよ。ただし、キャパシタンスCに初期電荷はないものとする。 以下の関係がt>0で成り立つ これをHeavisideの抵抗オペレータとベクトルで表すと ということになる。従って解を演算子法を使って導くと ということになる。従ってeR=eCとなる条件t=τは ということになり、CとRだけできまる。 |
| webadm | 投稿日時: 2012-1-23 4:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:RC直列回路 次もRC直列回路の問題。ただし以前の問題とは初期条件が異なる。
キャパシタンスCの初期電荷がQなるRC直列回路に対し、時刻t=0で直流電圧Eを加えるとき、流れる電流iを求めこれを図示せよ。 初期値問題として解くのが一般的で著者の解答もそうであるが、別解で解いてみよう。 線型回路なので重ね合わせの理が成り立つ。電源を取り除いてCに蓄えられた電荷がスイッチを閉じることによって流れだす電流と、今までの様に初期電荷が0の時に電圧が加えられた場合に流れる電流の合成が実際に回路に流れる電流である。 左の回路で以下の関係が成り立つ これをHeavisideの抵抗オペレータを使って書き直すと ということになる。 従って演算子法を使って解を導くと ということになる。 従って以前の問題で求めた右側の回路の解と重ね合わせの理で ということになる。 グラフに電流をプロットする場合にQの値によって3通りに描かれる。CE-Q=0の場合は電流値が常に0となるので割愛するとして、CE-Qが正か負かで二通り描く必要がある。 E=C=R=1として、Qを2(CE-Q<0)と-2(CE-Q>0)の場合についてMaximaで電流iをプロットしてみると 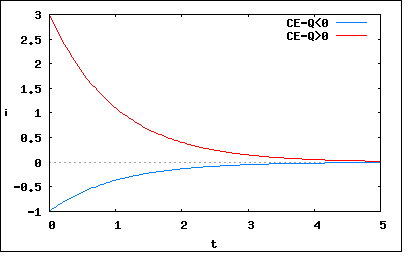 ということになる。 |
| webadm | 投稿日時: 2012-1-24 9:31 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
まだまだ:RC直列回路 次も前問の続きのような問題。
キャパシタンスCを電池Eで充電し、抵抗Rを通じて放電した。充電時の電圧と放電を開始してから15秒経過したときのキャパシタンスの電圧を比較したところ、その比は0.1であった。抵抗Rの値はいくらか。ただし、C=40[uF]とする。 キャパシタンスの電圧降下をeとして、初期状態の電荷は電圧Eで充電してあるためCEである。スイッチをR側に切り替えると放電が開始してRで消費される。従って以下の関係が成り立つ これをHevisideオペレータとベクトルで書き直すと ということになる。従って演算子法を使って解を導くと ということになる。 従って題意のe(15)/e(0)が0.1になる条件を満足するRの値は ということになる。 P.S 前問からすでに連立方程式の片方が微分方程式でなくなっているが、これは線型システムの状態方程式と呼ばれる。別々の方程式だが連立しているため、ベクトルを使って一緒に表すと大変見通しが良くなるため工学では多用されている。解を求める場合にも線型代数の手法が使える。更にHeavisideの演算子法を組み合わせるともはや敵無しといった感じに見える。 |
| webadm | 投稿日時: 2012-1-27 7:27 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
もうひとつの:RC直列回路 次も前問と似たような問題。
キャパシタンスCを電圧Eで充電し、抵抗Rを通じてT秒間放電したところキャパシタンスの端子電圧はE1に減少した。キャパシタンスCを求めよ。またE1=E/εなるに要する時間Tを導け。 というもの。 今度はCが未知定数となる。εは自然対数の底(exp(1))のことと思われる。 RC直列回路の放電電圧特性は前問で既に解いているので、それを利用しよう。別解で放電電流特性を求めていれば、Rの両端の電圧降下は回路上Cの両端の電圧降下と等しいので、e=Riとしてもよい。 題意よりT時間経過した時点で以下の関係が成り立つ 従って自然対数に変換するとCは ということになる。 またE1=E/εなる条件は ということなので、 ということになる。 |
| webadm | 投稿日時: 2012-1-29 0:18 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
またまた:RC直列回路 次もRC直列回路の問題だが少し毛色が違っている
RC直列回路に直流電圧Eを加えるとき、抵抗Rおよびキャパシタンスに供給される電力Pr,Pcを求めよ。またキャパシタンスにWc=CE^2/2のエネルギーを蓄えるには同僚のエネルギーを抵抗Rで消費しなければならないことを証明せよ。 というもの。 これまでは電流、電圧、電荷に関するものだったのが、電力とエネルギーに関するものに拡大されている。電力は電流と電圧もしくは電流か電圧の双線型形式で表され、エネルギーは電力の時間積分で表されることを思い出す必要がある。 電流の解はこれまでの結果より ということになる。従って抵抗RとキュパシタンスCに供給される電力はそれぞれの電圧降下に電流を乗じた瞬時値電力として ということになる。 従って抵抗Rで消費されるエネルギーとキャパシタンスCに蓄えられるエネルギーはそれぞれに流入する電力を時間積分して ということになる。 従ってt→∞でキャパシタンスCにCE^2/2のエネルギーが蓄えられるから、それまでに抵抗Rで消費されるエネルギーは と同じであることが確かめられる。 |
| webadm | 投稿日時: 2012-1-29 0:45 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
電荷量不変の理 次もCR直列回路の問題だがCが2つ直列に接続されていてそれぞれのCについて解析するというもの。
キャパシタンスC1,C2,を左図のように直列に接続し直流電圧Eで充電する。つぎにこれらのキャパシタンスを右図のように接続するとき、C1,C2の電荷の時間に対する変化を示す式を導出せよ。 というもの。 これはやっかいな問題である。というのも2つのキャパシタを直列につなぐと全体としては2つのCの合成容量をもったひとつのキャパシタとして等価であるが、その中間点についてはフローティングノードと呼ばれ電位が前後のキャパシタの電荷に依存し不確定となるためである。 回路シミュレータとかではこうした回路を解析できないものが多い。シミュレーターはキャパシタの初期状態を短絡かオープンのいずれかであることを前提としているので、いずれの場合でも中間点の電位は計算不能か現実と異なる。すなわちこうしたフローティングノードについてはシミュレーションができない。それでも解析的には厳密解が存在する。 左の回路で以下の関係が成り立つ これをHeavisideオペレータとベクトルで表すと ということになる。これを演算子法で解くと ということになる。過渡解が得られていないが、これは演算子法に限らない。というのも初期条件をq1(0)=q2(0)=0とするとt=0で電流が不定(無限大)となり、瞬時(t=+0)に定常状態になるためである。 従ってC1,C2の電荷はそれぞれ等しいということになる。当たり前のことのように出てきた結論だが容量が違っても蓄えられる電荷は等しいというのは不思議に見える。しかし定常状態では電流が流れないのだからC1とC2の電荷はバランスしていなければならない。という意味ではこれで正しい。 難しいのは右の回路の解析である。典型的な初期値問題だが、未知の関数が3つある点が今までの問題と異なる。 IQが低いので即座には関係式を導くことができない。問題を易しくして考えてみる価値がある。 例えばC1=C2の場合は右の回路ではどうなるか? C1とC2の充電後の電圧v1,v2は ということで等しくなり、Rには電流が流れないことになる。またC1,C2に蓄えられた電荷も初期状態のまま変化しないことを意味する。 つまりこれは答えの一歩手前を見たことになる。関数q1,q2,i1は共通してC1=C2の条件でゼロとなる項を含んでいることが明らかである。つまりq1,q2,iはそれぞれ以下の形をしていることが予想される これとは別に右の回路でキルヒホッフの電圧則から以下が成り立つ あと2つどうすんだこれ(;´Д`) 問題をややこしくしているのはC1とC2の極性が逆向きだから。これがもし充電時と同じ向きであれば、合成容量のCがRに接続された形になるので以前に解いた問題と同じRC直列回路となる。この場合にはCの電荷が尽きるまでRに電流が流れ続けることになる。 ところがC1とC2の極性が向かい合わせになっていると話しは違ってくる。どちらか電圧の高い方が低い方を充電する形で電流が流れる、そして電圧の低い方が充電されて電圧が等しくなるまで電流が流れ続ける。この場合は電荷が尽きるまで電流が流れるということはない。ここが大きな違いだ。 もはや単純な微分方程式の立式ではなく物理現象のモデル化という難問である。数学の本をいくら調べても参考になる答えは得られないだろう。自分で考えるしかない。 ややこしいことに片方のキャパシタは放電し、もう片方は充電されるということで互いの電圧が等しくなるまで電荷量が変化していく。更にややこしいことに、間に抵抗Rが入っているのでそこで電力が消費される。それは2つの電荷量の変化にどんな影響を与えるのだろうか? 難しい事を憶えてしまうと知識が邪魔をして簡単な問いに答えられない典型例である。 電気理論の初歩に立ち返ると、電流iは電圧の高い方のキャパシタC2が低い方のキャパシタC1を充電するために電荷を放出する速度に比例する。元来はC1とC2は直列に接続され電池で充電されたのだが、その際も同じ電流が流れて同じ量の電荷が充電されたことになる。これで最初にC1とC2が同じ電荷を持つという疑問は解消する。 良く考えると、キャパシタを直列に接続して充電した場合、電荷量は同じだが、電圧はキャパシタの容量に反比例する。より容量の大きいキャパシタは電圧が低くなり、容量の少ないキャパシタは電圧が高くなる。 ううむ今ひとつわからない。小学生だった頃に掛け算の99を全部言えないと下校させてもらえなかった時のことを思い出した(;´Д`)出来た子はさっさと帰るのに最後に残った落ちこぼれ組の一人だった。99はその後そろばん教室に通って自然に身に付いたけどね。無理矢理暗記というのがあの頃から苦手だった。 なんの話しだったっけ、ああ、残る2つの方程式ね。さながら電荷量と電流に関する式をたてればいいのだけれども、さっさとできない自分がここに居る。 (2012/2/2) 思考錯誤の上にようやくたどり着いたのは以下の関係式 C1に充電された電荷をC1の電荷から差し引けばC1の初期電荷となり、C2から放電された電荷をC2の電荷に加えればC2の初期電荷になるという簡単な理屈である。当たり前と言えば当たり前過ぎて思いつかなかっただけだった。 上の式から電流iを消去することも可能だろうけど、うまくいかなかったのでそれは読者の課題としよう(´∀` ) 上の関係式をHeavisideオペレーターとベクトルで書き直すと これを演算子法で解くと ということになる。 これは最初に予想した通りの関数の形になっている。 この問題は以下の図の様にC1とC2を口径の異なるが同量の水を蓄えたタンクに置き換えて、2つのタンクの底を水車をのあるパイプでつないだと考えるとわかりやすい。 q1,q2がそれぞれのタンクに蓄えられた水の体積(電荷量)とすれば、それをタンクの断面積(静電容量)C1,C2で割れば水位(電圧)が得られ、その差があるためタンクからタンクへ水(電荷)が移動する。C1から流れ出した水はC2に移動するだけで失われない。移動する際に途中にある水車を回転させる仕事をする(電力を消費する)。抵抗Rは水の移動に必要な時間を引き延ばす効果を与える。R=0だと瞬時に水が移動してしまうからである(理想流体の場合)。現実には流体は粘性がありそれ自身で移動抵抗を発生する。 なんだ簡単じゃないか(´∀` ) ふうこれでやっとぐっすり眠れる。 P.S 別解のアプローチとして他にも検討したのが、重ね合わせの理を用いるものと、C1,C2から合成される単一のCがRと並列に接続されるように回路を簡単にして、移動する電荷の量だけを考えるというもの。どれも途中までやって諦めたので、後は読者の課題としよう(´∀` ) P.S 水タンクのモデルは判りやすいが、新たな疑問を生み出すことになる。実際に実験してみると、水位が同じになった後もゆっくりと振動したり水が逆流したりすることが観測されるかもしれない。電気回路でも現実のキャパシタで容量の大きな電解コンデンサや電気二重層コンデンサなどの場合、同様に電圧が一緒になってもわずかな揺り戻しが観測できるかもしれない。水は理想流体ではなく均一に移動するわけではない、同様に現実のキャパシタも高誘電体になればなるほど、電荷が均一に蓄えられているわけではない。電荷の移動の速度が速いと移動速度が場所によって異なる。それが後で揺り戻しが起きる原因となる。キャパシタでは誘電回復とか呼ばれている特性である。現実の受動素子は実は皆非線形素子なのである。 |
| « 1 2 (3) 4 5 6 7 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

