| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2012-5-7 2:09 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RLC直並列回路 前問で基本的なRLC素子の組み合わせの回路はお終いで、これからはその応用というか直並列混成回路の問題。
図の回路に直流電圧Eを加えるとき、回路に流れる電流が非振動的となるような抵抗Rの臨界値を求めよ。ただし、抵抗Rが無限大のときの過渡電流は振動的であるものとする。 というもの。 RL直列回路とRC並列回路がシリーズ接続された回路に電源電圧Eがステップ入力されると考えることができる。 以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 従って題意の非振動的となる臨界値のRは以下の条件を満足する必要がある ということになる。この式から2箇所存在することになる。 またC,R,L,rはそれぞれ正の実数であり、Rは無限大であってはならないことから第二の式には更に以下の条件が加わる 従って最終的なRの条件は ということになる。2つめの解は括弧内の条件を満たす場合のみ存在する。 具体的な例としてr=C=L=1の場合には最初の解のみ存在し、r=C=1,L<1/4とした場合には2つの解が存在することになる。 残念なことに著者はRの解を求める際にRの多項式の一次項の係数が負なのを見落としており、まったくとんちんかんな結論を導きだしてしまっている。それがなければ、分子と分母が約分できる式になって上記の様な結果になるはずだった。 P.S 過減衰、臨界減衰、不足減衰を判定する判別式を幾何学的にとらえると面白い。r,C,L,Rの4変数関数であり、その零点が臨界減衰条件となる。簡単にr=C=1,L=1/5としてRを正の範囲で変化させると、2つの零点があるのを確かめることができる。Rが0に近い方の点は関数値の変化が急峻でMaximaでは実軸と交わるあたりをプロットすることができない。臨界減衰点は不足減衰領域と紙一重である。0から遠い点は幾分なだらかで零点の存在が確認できる。後者は第二の解である。4変数の組み合わせによって無数に臨界減衰点が存在すると思われるが、それを計算で求めるのは容易ではないことはすぐわかる。 |
| webadm | 投稿日時: 2012-5-8 8:31 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続:RLC直並列回路 次もRL/RC混成回路の問題
以下のような定常状態にある回路のスイッチをt=0で開いた。流れる電流を求めよ。 というもの。 定常状態なので、Lには電流が流れCには電流が流れていないということになる。つまりLには鎖交磁束がCには電荷が蓄えられた状態で均衡していることになる。 従ってこの問題はLとCに初期エネルギーがそれぞれ蓄えられた状態を初期条件とする初期値問題である。 定常状態でLに流れる電流はE/RLであることは明らか。従ってLに蓄えられている鎖交磁束はL*E/RLということになる。 一方Cの両端の電圧は電流が流れていない状態で電源電圧と均衡しているのでEということになる。従ってCに蓄えられている電荷はC*Eである。 これらを初期条件とすればスイッチを開いた後に残る閉回路内で以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。途中の式は長く収まりきれないので省略した。確認するのは読者の課題としよう( ´∀`) この結果が正しいことは先の積分方程式を両辺微分して得られる連立同次微分方程式を初期値問題として解くことによっても確かめられる。これはMaximaで以下の様に簡単にできる。 はっきり言おう、断続部の無い問題ではMaximaが最強だ(´∀` ) 上記は過減衰のケースで臨界減衰の場合には以前の問題のように極限操作によって ということになる。 残る不足減衰のケースではべき根が純虚数になるので ということになる。 C=L=E=1,RL=RC=1/2とすると振動的になるのでプロットすると 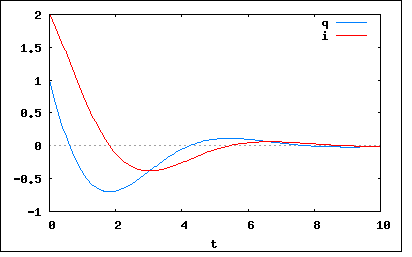 ということになる。 回路シミュレータで同じ条件でシミュレートした結果も厳密解とよく一致している。 RL=RCだと電流の第二項が消滅してしまうので、RL=1/2,RC=0として第二項が残るようなな回路にすると 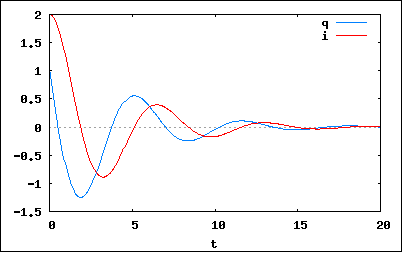 ということになる。抵抗値を減らしたので時定数が長くなり静定までに要する時間が長くなり、消費される電力も少なくなるのでより振動的となっている。 よく見ると電流/電荷の零点は常に他方の極大極小点と一致している(sinとcosの関係だから当然)。電流の零点は磁束の零点であり電荷極大極小点、逆も真なり。典型的な調和振動子である。 こうしてみると現代では回路の過渡応答の厳密解を解析的に求めるよりもシミュレータで動かしてみたほうが簡単だし速いしグラフも綺麗じゃんということになる。しかしまったく解析が不用かというとそうではなく、シミュレーターの結果が妥当かどうかは人間の判断によるので、やはり最後は解析で有る程度の当たり外れを判定する必要は残る。 |
| webadm | 投稿日時: 2012-5-12 18:14 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:RLC直並列回路 次の問題もRLC直並列回路だが少し捻ってある
以下の回路のスイッチを閉じた瞬間から常に電池Eを流れる電流が一定であるにはR1,R2,L,Cの間にどういう条件が必要か。 というもの。 回路は一見すると前問と同じ、RL直列回路とRC直列回路が並列接続されたもの。 電池Eに流れる電流はRL直列回路とRC直列回路それぞれに流れる電流の和であるから、今まで学んだ結果から暗算でも求めることができる。しかし題意はその電流が一定になる素子定数の条件を求めよというものである。 すぐにこの問題は回路が定抵抗回路となる条件を問うているのがわかる。 ストラテジーとしては、直接回路の複素周波数領域でのインピーダンスが定抵抗となる素子定数の条件を直接求めてしまう方法と、過渡電流の解からそれが時間に依存しない定数となる素子定数条件を求める方法がある。 著者は後者の方法なのでそれとは別解でやってみよう。 問題の回路の複素周波数領域でのインピーダンスは ということになる。 従ってインピーダンスが複素周波数に依らず定抵抗となる条件は、第1項がゼロである必要から ということになる。 すなわち ということになる。 なんだ簡単じゃないか( ´∀`) 著者はR1=R2とR1/L=1/CR2とだけの結論だが、実際には美しい関係式が潜んでいることを見落としている。 P.S 演算子法を使った別解もある 電池に流れる電流i,Lに流れる電流i1,Cに流れる電流i2の間に以下の関係が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと 解を求めるまでもなくこの時点でi(t)が定数になるための条件は第一項と第二項の和がゼロになる必要から ということになる。すなわち ということになる。 ちなみにこの√(L/C)は単位が抵抗と同じΩであることから、特性インピーダンス(characteristic impedance)と呼ばれる。特性インピーダンスという用語を最初に用いたのはHeavisideである。一定値の特性インピーダンスを持つ伝送路をその特性インピーダンスで終端することによって長距離でも歪みなく信号を伝える同軸ケーブルの原理を発明したのもHeavisideである。 |
| webadm | 投稿日時: 2012-5-13 1:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RL直列回路(交流入力) 次はRL直列回路に戻って今度は直流電源入力ではなく交流電源入力の問題
RL直列回路にt=0で正弦波電圧e=Em sin(ωt+θ)を加えた場合の(1)電流iを求めよ。(2)電流の過渡成分が0となるための条件を示せ というもの。 以下の関係が成り立つ これをHeaviside演算子で書き直すと これを演算子法で解くと ということになる。久々に三角関数の加法定理を使った。 ここで題意の過渡電流は第二項の指数関数を伴った過渡項でありt→∞で0に収束する項のことである これがゼロになる条件はsin項が0になる条件 ということになる。 R,Lは共に実数で≠0であるとすればφはωによって、0≦φ<π/2の範囲の値を取る。θが、nπ≦θ<(n+1/2)πであれば少なくとも過渡電流はゼロとなるωが必ずひとつ存在することになる。(n+1/2)π≦θ<2nπの範囲では条件を満たさないばかりか、定常状態での最大電流がスイッチを入れた瞬間に流れてしまう可能性があるということになる。 これは何に役立つのだろう。電力システムとかで遮断器を投入する際に上記の条件を満たすタイミングで遮断器を投入すれば有害な過渡電流が流れずに綺麗に電力回路がつながることになる。負荷が定抵抗回路でない限りは交流電源を投入する場合、上記の条件を考慮しないと意図しない過渡電流が流れるということを意味する。零相投入(θ=0)ではだめなのだ! |
| webadm | 投稿日時: 2012-5-13 22:24 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続:RL直列回路(交流入力) 次は前問の逆問題
抵抗R=75[kΩ]とインダクタンスL=30[mH]の直列回路に周波数f=50[kHz]の正弦波電圧を加えるとき、過渡電流を生じないためにはこの正弦波をどのような位相で加えればよいか。 というもの。 前問では過渡電流を生じさせない条件を導いたが、今度はそれを利用して、交流電源の位相θを決定するというもの。 予め与えられた素子定数からφを計算すると ということになる。 従って前問の過渡電流を生じさせない条件より ということになる。 著者はn=0に関する解しか与えていないが、実際にはそれと逆相になる点も解である。 |
| webadm | 投稿日時: 2012-5-13 23:03 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
続々:RL直列回路(交流入力) 次も前々問の続きで少し捻った問題
RL直列回路に正弦波電圧を加える場合、電圧が0となった瞬間に加えるときと、電圧が最大になったときに加えるときでは電流の最大値の比はどうなるか。ただし、抵抗Rの値はLのそれにくらべて十分小さいものとする。 というもの。 これは零相投入と最大値投入の比較論に関する問題である。既に零相投入では過渡電流を避けることが出来ないというのは知っているの。 問題はそれだけではなく、RとLの関係にある前提条件がついているところである。R≪Lということである。 この条件を適用して前々問の電流の式を電圧が0と最大値の時のそれぞれについて導くと ということになる。 これをEm=L=f=1でプロットすると 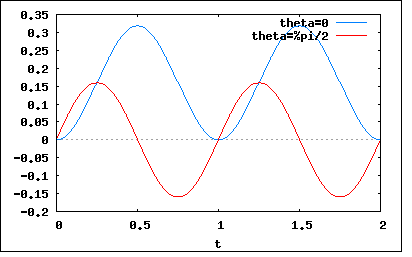 ということになる。 これは極大点を求めるまでもなく最大値は 従って両者の比は ということになる。 零相投入すると最大値で投入するよりも倍の最大電流が流れるという驚愕の事実が証明されたことになる。 直感的には零相投入の方が良い気がするが、実はそれは誘導性負荷に関してはまったくの誤りであるということが判明したことになる。 回路シミュレーターで2つの電源投入パターンに関してシミュレーションしてみると ということになる。零相投入した場合、電流が永続的な過渡電流によって+側に完全にシフトして脈流になってしまっているのがわかる。それに対して最大値で投入した場合には過渡電流の影響はまったく見られず正弦波交流のままとなっている。 この結果から誘導性負荷に交流電源を接続する際の位相が不適切だと、定常時の倍の最大電流が流れるということがわかる。回路にフューズが挿入してある場合、2倍の定格でないと吹っ飛ぶことになる。 昔は真空管のラジオやテレビがあって、皆電源トランスを備えていた。それらは商用交流電源から見ると誘導性負荷のため、ラジオやテレビのヒューズの定格を決めるのには、上記の考慮が必要になる。そうでないとスイッチを入れるタイミングによってはフューズが即飛んでしまうことになるからである。 今日的には家電製品は皆半導体回路になってしまったので、もっと事態は複雑である。ヒューズとかは無いのが多いのではないだろうか。パソコンとかでフューズが飛んだとかいう話しは聞いたことがない。その代わり火を噴いたとか、爆発したとかいうのはよくある。 電力回路とかで誘導性負荷と並列に力率改善用コンデンサを必要に応じて接続することがあるが、何の工夫もしないと想定外の電流が流れることになる。こうした力率改善用コンデンサは電力需要家の設備になるので、投入時の位相を制御するような高度な装置の導入は望めない。したがって、過大な電流が流れた時にそれを制限するためにコンデンサの端子に低インダクタンスだが大電流が流せるコイルを直列に接続してあることが多い。これによって過渡的に大電流が流れた際にコイルに電流を投入前の状態に保とうとする逆起電力が発生することになる。コイルのインダクタンスはそれ自身がその後悪影響を及ぼすような大きなエネルギーを蓄積することはない低い値に設計される必要がある。 |
| webadm | 投稿日時: 2012-5-14 8:11 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RC直列回路(交流入力) 今度はRC直列回路の交流入力に関する問題
図のようなRC直列回路にt=0から正弦波電圧e=Em sin(ωt+θ)を加えるとき、抵抗RおよびキャパシタンスCの端子電圧はどうなるか。また過渡現象を生じないための条件を示せ。ただし、この回路は静止状態であるとする。 というもの。 以前のRL直列回路と異なるのは問われているのが電流ではなくRとCの端子電圧である点。それと静止状態とは、Cの初期電荷が0ということだと解釈しよう。 抵抗Rの端子電圧VrとキャパシタンスCの端子電圧に関して以下の関係が成り立つ ということになる。 これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 ω=C=R=Em=1としてプロットしてみると 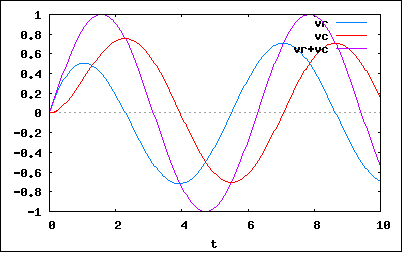 ということになる。過渡現象が現れているのが見てとれる。 回路シミュレーターの結果も厳密解と一致している。 従って過渡現象を生じない条件は、上記の解の過渡項が消滅すればよいので ということになる。 ω=C=R=Em=1のケースではatan(1/ωCR)=φ=π/4であるので、上記の条件を満たすθはπ/4と5π/4ということになる。 θ=π/4としてプロットしてみると 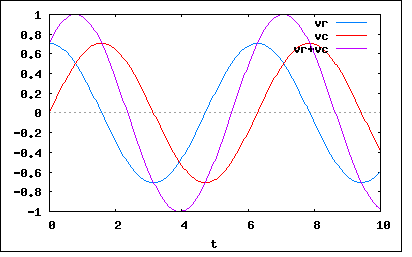 綺麗に過渡現象が消滅し定常状態と変わらないのが見てとれる。 回路シミュレーターの結果も厳密解と一致している 著者は何を勘違いしたか、題意で求められている電圧ではなく電流の解を求めてしまっている。過渡現象が起こらない条件はあっているが、これだと点数は半分しかもらえない。 P.S 部分積分を計算した後、分母の(ωCR)^2+1を開平して係数として残るようにしないと振幅がωや素子定数に依存しないという誤った解が導き出されてしまう。このあたりが演算子の非可換性と併せて演算子法の落とし穴でもある。解法としてはストレートで線型代数による連立方程式の解法とシームレスにつながるのだが注意を怠り安易な道を選択すると落とし穴に墜ちる。この辺りは後にLaplace変換を学ぶ際にでも整理することにしよう。 この種の問題の解を実際の回路と測定器だけを使って試行錯誤的に見いだすのは困難である。例えある素子定数での条件が見いだされたとしても、それと異なる素子定数での解はその結果から直接導くことはできない。解析的な手法が依然として不可欠なのはこの理由による。 |
| webadm | 投稿日時: 2012-5-19 19:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
LC直列回路(交流入力) 今度はLC直列回路の交流電源版
LC直列回路に正弦波電圧Em sin(ωt+θ)を加えるとき、流れる電流iおよび電荷qはどうなるか。ただし、この回路は静止状態にあるものとする。 というもの。 以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 部分積分とEularの公式、それに微分が出来れば解が得られるとはいえ、たかがLC直列回路の解析にこれほど長い数式を扱わなければならないので公式の記憶違いもあってなかなか難航した。 最終的な解は想像を超えた形をしている。 LC直列回路は純粋なリアクタンス回路なのでエネルギーを消費する抵抗がないためt→∞で消滅する過渡項が無い。 Em=C=L=1,ω=2、θ=0としてプロットすると 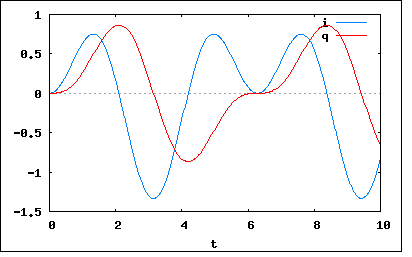 ということになる。 一瞬目を疑うが、式の上だと周期の異なる2つの正弦波が重なりあってうねりを生じている。 回路シミュレーターで同じ条件を試してみると、厳密解と一致している。 |
| webadm | 投稿日時: 2012-5-23 4:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RLC直列回路(交流入力) 次はRLC直列回路の交流版
静止状態にあるRLC直列回路にt=0で正弦波交流を加えるとき、流れる電流iおよび電荷qを求めよ。 e=Em sin(ωt+θ) というもの。 前問に回路にRが挿入された形。現実のLC直列回路は実際には内部抵抗を伴うのでRLC直列回路となる。 以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと (2012/5/26) この問題に至って計算がかなり困難になっている。これまでも直流電源の場合には似たような逆演算子の形は登場したが、今回は電源が正弦波交流ということで直流の場合と違って定数ではなく積分の外に出すことができない。これが計算を複雑にしている。 まずは以下の共通の積分を計算しておこう ということになる。 従って解は 式の最初の部分はすぐに三角関数の合成定理を思いついて簡単に整理できたが、残りの部分を著者の解と同様に整理するのにかなり時間を要した。多項式を分解して整理し直せば同じ合成が適用できるという事実を発見してなんとか見通しがたった。mimetexが扱い切れないので後半の処理は以下に示す。 ということになる。 だいぶ式を操作する過程で転記ミスや誤記が頻発してなかなか確信のもてる結果が得られなかったが、検算にMaximaを使用するなどしてやっと最終形にたどりついた。 この時点で著者の電流に関する最終解に明らかな誤り(転記ミス)があるのを発見した。 ここまでは過減衰のケースなので、以前にもやったようにこれをベースに臨界減衰と不足減衰のケースの解を導くことができる。 臨界減衰のケースの解は、過減衰の解をβ=sqrt((R/(2*L)^2-1/(C*L)→0へ極限以降することにより ということになる。 不足減衰のケースはβ=jγと置き換えればよく ということになる。 θ=0,ω=1,Em=C=L=1,R=10とおいて過減衰のケースをプロットしてみると 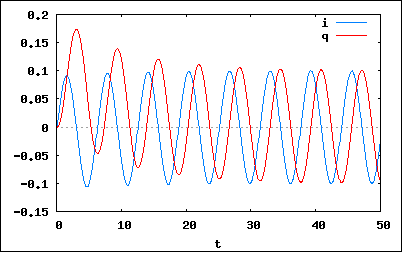 ということになる。 同じ条件で回路シミュレーターによる結果も上の厳密解とよく一致している。 意外にも電流は定常時とほとんど変わらないが、過渡現象は電荷によく現れている。 今度は同じ回路でR=2として臨界減衰についてプロットしてみると 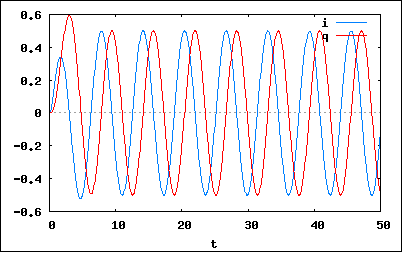 ということになる。過減衰のケースより早く定常状態に至っていることがわかる。 最後に同じ回路でR=1,L=2として不足減衰についてプロットしてみると 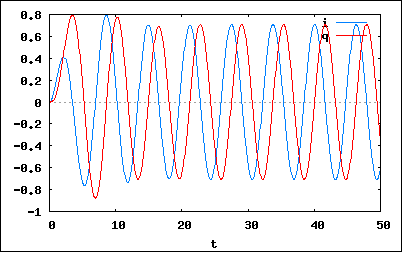 ということになる。電源よりも幾分長い周期で振動が見られアンダーシュートとオーバーシュートが確認できる。 ここにきて、たかがRLC直列回路とはいえ電源が時間の関数になるだけで、解析は困難を極めるようになった。回路シミュレーターではほとんど労力なく同じ結果を得ることができる点で現代の技術者は恵まれすぎているのかもしれない。 |
| webadm | 投稿日時: 2012-5-28 23:28 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
RL直並列回路(交流入力) 次も面倒そうな交流入力のRL直並列回路の問題。
下図の回路でt=0でスイッチを閉じたときの電流を求めよ。ただしe=Em sin(ωt+θ)とする。 というもの。 以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ここまでくると、共通の積分項だけ計算すれば、あとはスケール係数が異なるだけだとわかる。積分項の計算は前問の公式がそのまま使える。だが('A`)マンドクセ Maximaは最初の微分方程式が式が複雑すぎて解けないとギブアップしている。検算が簡単に出来ないじゃないか(´Д`;) 共通の積分項について予め公式を求めてしまおう 同様に ということになる。 (2012/6/16) ここまでの結果は以下が成り立つことをMaximaで検算済みであり正しい結果である。 なんだか前問のおさらいみたいになってしまったが、これらの変換公式を先の途中までの解に適用すれば...('A`)マンドクセ (2012/6/17) 著者の解には誤植はあるものの、解法自身は答えの一歩手前である定常解を定常解析で得た後、残る過渡解を同じ回路で直流入力のケースの以前の問題の一般解の式を適用して求めており妥当である。最後の答えは定常解が最初に見通していたのと違っていたり誤記(ほとんどは原稿ミスだと思われる)が多いが、大筋ではあっていると思われる。 問題は演算子法で正しく導いたはずの上の結果が、どうしても著者の結果と一致しないことにある。定常項は一致しているが、過渡項が微妙に違う。 可能性としては演算子法での導出にflawがあるということになるが、あるとしたら演算子の適用順序だろうか。ううむ、わかんね(;´Д`) 以前の直流入力の同じ回路の問題も投げ出したけど、これも投げだしそうな雰囲気。 (2012/6/20) もうそろそろ諦めたほうがよいかもしれない。以前にも同じ回路で直流ステップ入力の場合にも式が複雑になって諦めたが、今回は入力が正弦波のステップ入力と更に複雑になっている。 古い演算子法の本には、これまで用いたストレートなアプローチとは違った短縮アプローチが紹介されている。この問題で言えば、入力関数がステップ関数と正弦波関数の積であるので、予めそれらを演算子表現に変換してしまうというもの。正弦波は超越関数であるが、Eulerの公式で指数関数表現に書き換えることができる。指数関数は更に演算子pの有理関数に置き換える事が出来る。しかし事はそれほど簡単ではない。ちょっとやってみるとわかる。 と書き直すことが出来るので、これを最初の作用素方程式に代入すると 従って演算子法で解くと もはや部分分数に分解してやるには複雑過ぎるので、Heavisideの展開定理にご登場願おう(;´Д`) N(p),M(p)が互いに既約なHeaviside演算子pの多項式でM(p)/N(p)が部分分数に展開できる場合、以下が成り立つ ここでpkはN(p)の零点(根)である。 従って先の解の分母の演算子多項式の零点は であるからして...('A`)マンドクセ (2012/7/23) 今頃になって、上のMの式に転記ミス(ωpcosθをωcosθとしていた)があることに気づいた...orz なので修正した上で、もう一度やり直す必要があるため、従来の途中までの式は一端取り下げた。Maxima上ではM(0)/N(0)=0となっていたので初期の頃はMを正しく入力していたと思うが、後に何度かやり直した際に誤った式を参照するようになっていたのでどこまで合っているか定かでなくなった。 ということになる。(2012/7/31) 電流i3は上の式でR3をR2へL3をL2、φ2をφ3へI2mをI3mに置き換えるだけなので、長いので割愛。 ふう、ようやく著者の解法が導こうとしていたのと同じ結果が得られた。長かったよ(ノД`)ママン まるで数式と関数のジグソーパズルだった。IQが低下しているので式が丸ごと頭に入りきらずに、Maximaで計算した式を紙の上に書き写しそれから手作業でパズルを解いた。 苦労して解いた割りには、過渡解は単調に定常解へと遷移していく、驚くほどの結果ではなかった。大きな電源トランスをもった機器に電源を入れた際に最初ぶーんという音がして次第に小さくなっていく理由がこの式に表されている。電源を入れた直後は電磁石を作りだすような片方向の電流が流れ、次第に交流電流になっていくためだ。 実際に解の式をプロットしてみたり、シミュレーターの結果と比較するのは読者の課題としよう( ´∀`) 著者の解法は、最初に答えの一歩手前を定常解と定係数系常微分方程式の一般解の公式から求め、巧妙に積分定数を求めるエレガントな方法だが、最後に示された解の式は最初に提示された答えの一歩手前とは誤記誤植によってまったく正解からほど遠いものになっている。ゲラ刷りがノーチェックだったのか、著者の原稿段階で既に誤記があったかどちらかだろう。著者のとった方法も実際にやってみると最初にあっさり書かれている定常解を導くのも苦労する。 演算子法でも同じ結果が得られることが示せてよかった。前半部でとった畳み込み積分への帰着アプローチにはどこか数式操作にケアレスミスがあるに違いない。基本的には同じ結果が得られるはずだ。それにしてもストレートなはずの演算子法は素子が増えただけでだいぶ困難を極める。それでもまだ解が解析的に求められるから受動素子回路のみの回路は簡単である。これが能動素子を伴う電子回路だとそもそも解析的には解けないという事実が待ち受けている。 P.S この問題の回路と双対なCR回路が存在する。電圧が電流にLがCにRがGに直列が並列に、並列が直列に、電圧源が電流源に置き換えることによって双対な回路になる。 いずれにせよ試験で100点満点をとらせないための問題としては好都合である。毎年互いに双対な回路を交互にだせる。 |
| « 1 ... 3 4 5 (6) 7 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

