| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2016-7-26 20:20 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 自分の数学を持つことの勧め 前の議論の最後を再掲して続きを、
それぞれの双対基底は定義から以下の関係が成り立つことが要請される、 また先の基底変換の関係から以下の関係が成り立つ、 この2つの関係式より 従ってやや強引だが、双対基底に関する以下の座標変換の関係式が得られる これは行列表記の濫用だが、良く見るとこれは前出の反変ベクトル成分が受ける座標変換の関係式とまったく同じ形をしているのは注目すべき点である。 これで準備は整ったようだ。 (2016/7/30) ふう、あじー(;´Д`) 夏風というか新手のウイルスに感染したらしく下痢と喉の炎症、鼻水が止まらない状況。 なるだけ横になっていたいけど、眠れないし、眠っても鬱になる夢でうなされるし(;´Д`) 昔カウンセラーから鬱っぽいいやな夢は思い出さないようにってアドバイスを受けたことが記憶に残っています。 それでも思いだすと、今の職場で進捗が悪くてなんとか少しでも進展を見いだして報告したら、「高い金もらっていながら、結果はそれだけか、品質保証のかけらもないな」的な批判かパワハラ的な言葉を投げつけられて一気に気が滅入って自信とやる気を喪失、頭が真っ白になったところで、その人が実際にはそこには居ない昔の会社の同期の顔だったので疑問が生じました、それに批判されている品質保証に関してとっくに別プロジェクトで対策ツールが出来てだいぶ前から使われているし、なんかおかしい?と気付いたところで目が覚めて、夢だったことが判明。 また危うく鬱症状再発の危険を逃れたのでした。 みんなも不快指数の高い日はメンタル的に弱くなるので気をつけようね。 さて話を元に戻そう。 手元のテキストではすべからく、ここからの展開はテンソルの言葉(添え字表示)を使って簡潔に結果だけ示しているが、ここでは例によって泥臭い計算を行うことにする。この方がちゃんと結果が導出できるし、確かめることもできる。 ここで先の基底変換の結果を代入すると ということになる。(実際の計算は紙の上でやると転記ミスが絶えないので Maximaを使ったのはご容赦) 従って上の結果から基底変換行列式に関して再び以下の既知の関係式を得ることが出来る。 以前に一般の斜交座標系における基底ベクトルのスカラー三重積の関係から導いた結果と同じである。 ここで重要なのは、座標変換後の式に計量テンソルの時には無かった基底変換行列の行列式が出てくる点である。 正規直交系から一般の座標系への基底変換ではD=1、D'が基底変換行列の行列式と同値であるのと、更に正規直交系の間の直交変換ではD'=1となるため真相が隠れてしまっていた。 一般の斜交座標系の間の基底変換を考えることで、やっとそのことがあらわになるわけである。 さてこれで少なくともLevi-Civitaテンソルが計量テンソルとは違う座標変換を受けることが明らかになった。 最後にLevi-Civitaテンソルが一般の斜交座標系の間の基底変換でどのような変換を受けるか計算してみればいいことになる。 ここまでの結果をLevi-Civitaテンソルとテンソルの言葉(添え字記法)を使用して、慣れないEinsteinの総和記法を用いずに書き直すと、 ということになる。 従ってLevi-Civitaテンソルは以下の座標変換を受けることになる、 従ってLevi-Civitaテンソルは、真性テンソルではなく、重み1の相対テンソルまたは擬テンソル、もしくはテンソル密度に分類されることになる。 もともとε'ijkとεijkは同一の成分を持つので上の結果は結局ε'ijk=εijkでもあるわけで、真性テンソルの場合の成分の変換式と比較しやすいように上のようにわざわざ変換行列式を展開しているわけである。このあたりが一番納得がいかないかもしれないが、意図がハッキリすれば納得する。普通のテキストでは数式の意図は隠しているのでますます理解困難である。 重みのあるテンソルは狭義のテンソルの定義をLevi-Civitaテンソルのような擬テンソルも包含できるように拡張した概念だということが判る。 とうとうテンソル代数の最終章まで自分数学で辿りついたことになる。他にも枝葉的な議論(Levi-Civitaテンソルは計量テンソルによる添え字の上げ下げの関係にない等)があるが、それは読者の課題としよう(´∀` ) ここまでの議論は学校の講義とかではコマ数が足らないのと、それの応用は大学院でやることになっているので、この種の議論は大学院まで先延ばしするということになる。大学院に入ると何故か知っていることを前提に応用の議論が始まるのはお約束。 結局自分で納得するまで自分の手と頭を使って理解するしかないんだよね。 自分数学で大事なことはいかに有名な著者や優れていると評判のテキストでも、その内容でしっくりこないものがあったら、自分に正直に自分のやり方で同じ結果を導出できるかチャレンジすることである。 大御所が書いたものだから間違いはないだろうけど、どうやってそうした結論が出てくるのか導出方法までは書いてないことが大半なので、納得いかなければ自分で導出するのが一番である。 ということで、ここまで来てもまだテンソル代数の議論の範疇であり、まだベクトル解析やテンソル解析はこれからの議論である。 普通のテキストではここまでの議論の様に直線座標系でのベクトル代数やテンソル代数の話をして、すぐに曲線座標系での解析の議論に入る。 しかし以前に書いた通り、直線座標系と曲線座標系との間の座標変換は、直線座標系内での座標変換と違って線形ではないという事実はほとんど直接触れられていない。 ここに大きなギャップがあるので、まるで曲線座標系(もしくは特種な直交曲線座標系)でご破算で願いましてはと言って、最初から議論をやり直されているように写るのは当然である。 森さんの「ベクトル解析」のように、このギャップを埋めるために直線座標系での比例関係が、曲線座標系でも局所的に成り立つということを納得させるために、ほとんど大半のページ数を割いている。 数学的な観点だと、最初から議論を最も一般的な複素数での曲線座標系で始めるべきだということになる。確かにそうすれば途中の特種な座標系の結果も包含しているので、特種から一般へという手間はかからない。しかし最初のハードルが高すぎるので数学者でない限り無理だろう。 初学者はやはりGaussのやり方に習って、特種から一般への議論展開をするのがよさそうである。 学校では様々の教える立場と流儀の違いによって、ここでやったように直線座標系(正規直交系と一般の斜交座標系)でテンソル代数を議論するのと、テンソルとかを持ち出さないで直線座標系でも曲線座標系でも局所的な正規直交座標系でのみ議論するやり方がある。 前者のやり方は以前に参考書として紹介した岩堀長慶「ベクトル解析」に見られる。それ以外の薄い、お手軽なベクトル解析の入門書はいずれも後者のやり方になる。後者では基底ベクトルは全て単位ベクトルになるので、擬ベクトルとか擬テンソルとかの面倒な概念は持ち込む必要がなくなる。つまり観光バスにのって見所だけ短時間に見て回るということになるので見て回る者にとっては本当に隅々まで見たわけではない。 ということで、ここからはこれまでの議論を一般の斜交座標系からシームレスに直交曲線座標系への一般化にチャレンジすることになる。 いろいろなテキストを見る限りでは、ここまでの斜交座標系での議論で発見した数学的な対象が直交曲線座標系でも存在することが判っているので、うまくつながるのではないかと目論んでいる。 (2016/8/15) 元々の電磁気学をマスターするというモチベーションには変わりないが、だいぶ脇道街道をまっしぐらという感じが否めない。 ここらで、少し方向を電磁気学の方に向けないといけないだろう。 それと併せて、ここまでの成果を最大限に生かして、ベクトル解析へシームレスにつなげていくことにも挑戦しよう。 大抵のテキストは正規直交座標系でのベクトル代数のおさらいをした後に、直ぐにベクトルの微分を導入するか、ある媒介変数の関数としてベクトルを定義し直しているが、どれも議論のショートカットであることには変わりない。 何故微分なのかとか、なぜ新たな媒介変数の関数としてベクトルを定義し直さないといけないのかという意図に関しては一切触れていない。 それでは納得行かないままであるので、ここではそのギャップを埋めることを考えることにする。 今までベクトル代数で対象にしてきたのは、大きさも向きも延々に固定された動かないベクトルであった。 動かないままのベクトルで何が都合が悪いのだろうか? そう考えると、動かないままのベクトルが動いているように見える状況があることに気付く。 それは相対性理論に関係するのだけど、ある座標系(正規直交座標系でなくても局所線形ならなんでも良い)上に動かないベクトルが存在するとする(それは電位勾配ベクトルでも良い)。 その座標系上の任意の位置からベクトルを観測すると、それは永遠に動かないので一定の方向と大きさを保っている。 ところが、それとは別の座標系があって、先の座標系に対して相対的に座標の原点が時間と供に移動しているとする。その移動する座標系の任意の点から先の座標系にある動かないはずのベクトルを観測すると、向きが時間と供に変化しているように見える。 従ってある座標系上の動かないはずのベクトルは、別の座標系からは動いているベクトルに見える。それは時間を媒介変数としたベクトル関数そのものである。 そう考えると、とりあえず相対的に移動している座標系は何であれ、そこから動いているように見えるベクトルに関して解析が可能になる。 これでお膳立ては出来た。 後で図を書いてアップロードすることにしよう。 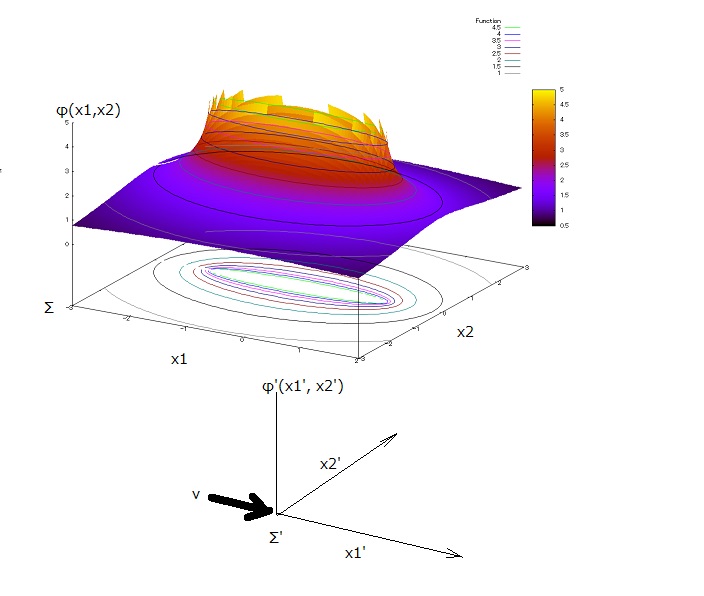 以前に演習問題を解いた時にMaximaを使って描いた静電ポテンシャルの等高線図を流用することにした。 北米のMonument Valleyにあるような景観を表すポテンシャル関数φを座標系Σ上で描き、それとは別に速度vで平行移動するもうひとつの座標系Σ'を考えた場合、Σ'上でポテンシャル関数φを観測すると、時間と供にΣ'座標系上の関数値は変化することになる。 これはMonument Valley内で車を走らせながら、景色を眺めたのと一緒で、時間と供に風景が近づいては後ろへ過ぎ去って行くように見えるのと一緒である。 これはEinsteinの相対性理論以前では、こちらが移動すれば周りの物は一緒に移動していない限り、こちらが移動しているのを逆の向きの速度で近づいて通り過ぎて行くというGalilei相対で説明でき、それで終わってしまっていた。 ところがポテンシャルが静電場である場合にはそれだけでは済まなくなることは、FaradayやMaxwellの仕事によって明らかだった。 以前に疑問に思って書いたことがあるが、如何にして電磁気学はNewton力学の反証となったのかという点がここに来てハッキリしてくる。 座標系Σ上では静電場しか存在しないのだが、移動する座標系Σ'からその静電場を観測すると、空間の静電ポテンシャルが時間と供に変化するので、時間と供に変化する磁場が現れるということである。 この議論はいきなり変動する電磁場の議論へと飛びすぎているのだが、正統なアプローチであると思われる。 扱っているのは静電場だけなのだが、別の慣性系から見ると静電場が時間と供に変化し、それに伴ってFaradayの電磁誘導則に従って時間と供に変化する磁場が現れることになる。 逆に座標系Σ上に静磁場があって、それを慣性系Σ'から観測すると、空間の磁場が時間と供に変化するので、元々は存在しないはずの電場が現れることになる。 もし座標系Σ上に静電場と精磁場が存在した場合、慣性系Σ'からそれを観測した場合、単純にそのどちらもが速度vで近づいてくるというGalilei相対性だけで説明できるものだろうかという疑問が沸く。 この疑問にアプローチして後に特種相対性理論と呼ばれるものを打ち出したのがEinsteinである。 Einsteinの示した慣性系Σ'から座標系Σ上の電磁場を観測した場合に慣性系Σ'上での電磁場がどう表されるかという式は複雑で、元の電場と磁場の成分が入り交じった複雑な形になり、およそGalilei相対のように単純に同じ形では物理現象が表せないというパラドックスを示すことになった。 Newton力学が正しいと信じれば、座標系が違うと物理現象が異なった形で表さなければならなくなる電磁気学はどっか根本的に間違っているという主張を裏付けることになる。 それにNewton力学の作用反作用の法則も電磁場では成立しない可能性がある。 後の一般相対性理論によってNewton力学が一般相対性理論の近似であって、厳密には修正を受けるべきものであることが明らかになるわけであるが。 こうした点は話が飛んでややこしくなるので普通のテキストでは絶対に触れないところであるが、電磁気学を理解する上で重要な点でもあるし、電磁気学を学ぶ上での不屈なモチベーションにもなる。 最終的にはこの疑問を自らの手で解決することにして、さしずめ座標系Σと座標系Σ'の原点が異なっていて動かないという特種な条件の下で、座標系Σ上のベクトル場が座標系Σ'上でどう写るか考えることにしよう。 最初に思い当たるのが、もし座標系Σ上のベクトル場が均一のものであったなら(空間のどの点をとってもベクトルの向きと大きさが一定なら)、座標系Σ'の空間上のどの点でも同様にベクトルの向きと大きさが一定に見えるはずである。 実際に実験室内で上記の様な均一な電磁場を作ることは容易ではない(十分な距離を置いて離れた二枚の無限大の面電荷もしくは平行した無限長の線電荷の作る電場は局所的に均一であると見なすことが出来るかもしれないが、一般には均一ではない)。 ここでは仮に均一な電場が得られたと仮定して話を進めることにする。 2つの座標系ΣとΣ'が供に正規直交座標系である場合には、ベクトル場が均一であれば、その大きさは座標系が変わっても保たれる。唯一ベクトルの向きだけは、座標系の回転によって変換を受けると予想が付く。 それを計算で確かめてみることにしよう。 (続く) |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| » |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

