| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2024-4-10 4:51 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
もうひとつの:直線上の点電荷と電気力線 2個の電荷 +mq(m>2)と-q とがあるとき、+mq から出発した電気力線のうち一部は -q に入りその他は無限遠に行く。-q に入るものと入らないものとの境界の電気力線は、+mq をどのような角度で出発するか? 電荷が 4q と -q のときはその角は60°になることを示せ。
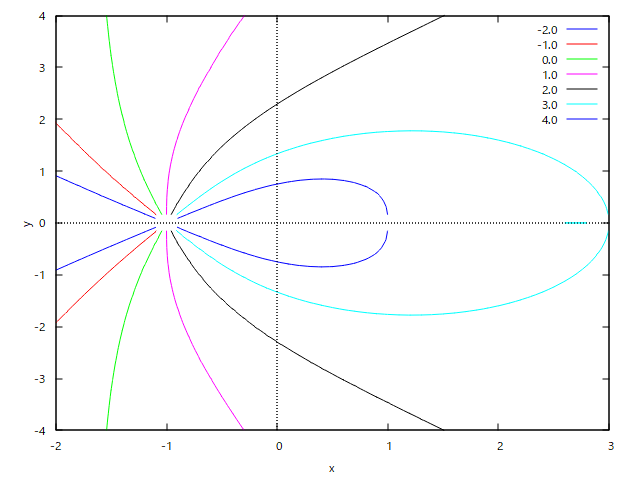 というもの。 これも前問で出てきたように、電気力線の点電荷の出発点の位置と、無限遠点で電気力線の陰関数が同値であることを利用することになる。 また上のプロットでは、右の点電荷(-q)から離れたところで2つの電気力線が鉢合わせしているように見えるが、著者の図ではそこのところがぎりぎりx軸上で無限遠点に曲がって並行に進み、決して同じ点電荷から出発した異なる電気力線は交わらないということを示している。 -q に入るものと入らないものとの境界の電気力線の条件ってなんだろう? ヒントとしては、電気力線の出発点は+電荷の点になるけど、電気力線は無数にあってそれぞれ全方位のいずれかの角度で出発することになるので、出発時の角度がひとつひとつの電気力線で異なっているということになる。 一方で無限遠点も無数にあり、点電荷からみて全方位の方向に無限遠点があることになるけど、-電荷の方向に向かった電気力線は(1)-電荷に到着するもの、(2)-電荷からそれて無限遠点に向かうもの、の2種類に分かれることになる。ぎりぎり-電荷に向かわずに無限遠点方向に逃げていく電気力線の無限遠点はx軸に並行となる(2つの点電荷を結ぶ直線に平行になる)ということが言える。 ということで電気力線の陰関数としては電気力線の出発点の角度と電気力線上の無限遠点と+電荷を結ぶ線分と2つの点電荷を結ぶ線分の角度を用いたものである必要がある。 上記の陰関数は前々問で出てきた気がする。 これだよな。しかしこれだと+mqからみた-q方向の無限遠点は0°方向になるので、sin値は0で矛盾するよな。 cosで書き直してみるテスト、 ということになる。 これを使ってみよう。 q1=mq, q2=-q として、+mpからθの方向で出発した電気力線が、-q方向に向かうもののぎりぎりで無限遠点に向かう電気力線では+mq, -qどちらか見ても電気力線の無限遠点は0°方向になることから、 ということになる。 題意のm=4を代入すると、 ということになる。 著者の解法とは異なるアプローチでもできたじゃないか(´∀` ) |
| webadm | 投稿日時: 2024-4-9 21:13 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
それでも:直線上の点電荷と電気力線 等量同符号の2個の電荷が2点におかれたとき、一方の電荷から両者を結ぶ直線に対してαの角で出る電気力線は無限遠ではどのような角度となるか、α=0°、90°、180°のときの値はいくらか?
というもの。 これは前問の結果を利用して、q1=q2としてαをそれぞれ代入して計算すればいいことになる。 α=0°の場合、 α=90°の場合、 α=180°の場合、 ということになる。 ぬるぽ(´∀` ) |
| webadm | 投稿日時: 2024-4-9 17:55 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
またまた:直線上の点電荷と電気力線 +q1,+q2 の電荷が A,B にあるとき、A 点から BA に対してαの角で出る電気力線は無限遠では BA に対して次の角をなすことを示せ。
というもの。 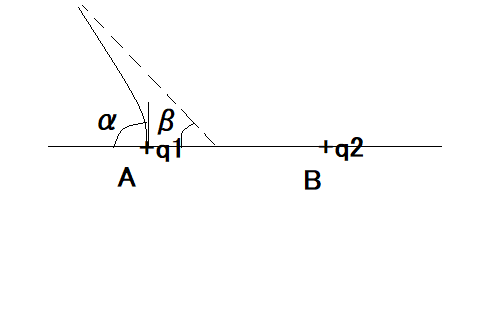 これも直線上の点電荷と電気力線問題のバリエーションで、2点電荷が同符号かつ電荷量が異なる場合に関するもの。 ストラテジーとしては前問の結果を応用して、同一電気力線上の2点(A,無限遠点)で下記の電気力線が満たす条件式が同値となることを利用すればいいことになる。 すなわち、 という関係が成り立つことになる。 両辺を開平して、βについて解けば、 ということになる。 なんだ簡単じゃないか(´∀` ) 前問と違って、ABではなくBAと成す角であることに注意が必要だった。 |
| webadm | 投稿日時: 2024-4-8 3:49 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
まだまだ:直線上の点電荷と電気力線 +q.-qの二つの電荷が点A,Bにあるとき、+qからABに対してθ1の角で出発した電気力線がABの垂直二等分面と交わる点をPとし、∠PAB=αとすると、次の関係のあることを示せ。
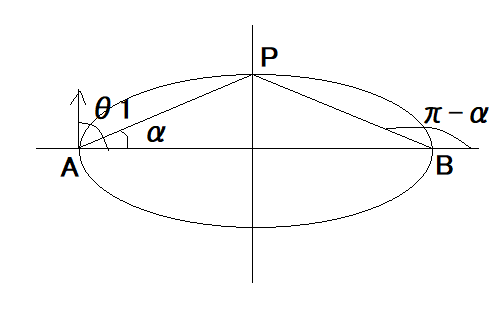 またしても直前上の2点電荷が成す電気力線に関する問題。よく考えつくよな。今度も電界と電気力線が等価な概念であることを導く解答を探してみよう。 著者の問題説明のための図が誤解を招き易い。 ∠PAB=αの場合、その場合のみ∠PBA=αとなるので、その補角はπ-αとなるので、Pが電気力線上の他の点の場合にはそれは成立しないという点である。 なのでこの問題は一般的なケースではなく、PがAB間の中点を通る平面と電気力線の交点にある場合のみの特赦なケースを扱うものであることに注意する必要がある。 この問題を解くヒントは、直線上の点電荷と電気力線の最初の問題の時に考えた、立体角のことを思い出す必要がある。 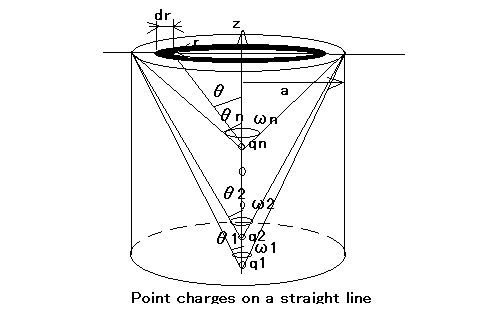 電荷qnに関するθnと電荷qnからθnが描く円盤を見た立体角ωnの関係は下記の通りだった。 従って本題意に即した形だと、 ということになる。 問題は題意の式ではα/2という半角が出てくるのだが、三角関数の2倍角の公式を当てはめて考えると、 これを先の立体角の式に代入すると、 ということで題意の式にもあるsin(α/2)でも表すことができることが解る。 話は変わるが、上と良く似た議論が昔読んだことがある、「場の古典論」ランダウ、リフシツ著の第7章の57節にある「広い光線束による結像」に出てくるのを思い出した。 つまるところ、点電荷から出る電束と電気力線の構図は、工学系(ひとつもしくは複数のレンズ)で物体から放たれる光を結像する構図と相似であるためと考えられる。 地球上の生命は人類がそれに気付くずっと何億年も前に眼球としてその理論を実用化していたのには驚かされる。 話を元にもどそう。 直線上の点電荷と電気力線の最初の問題では任意の電気力線が満たす以下の条件式を導出する問題だった。 この問題では、同一電荷量だが異符号な2点電荷が成す電気力線上の2点(A, P)において、上記の式が同値となることを利用すれば良いことになる。 すなわち、 が成り立つことになる。 ここで、先の2倍角の公式を使って二分の一角表現に書き換えると、 という関係が成り立つ。 両辺を開平すれば題意の式が得られる。 P.S 先にcosを二倍角の公式を使ってsin^2の表現にしても同じ結果が得られるはずである。 が同一電気力線上の任意の点で成り立つはずである。 従って、同一電気力線上の2点(A,P)において、 が成り立つことになる。 両辺を開平すれば、題意の式が得られる。 やればできるじゃないか(´∀` ) 2倍角のcosだけでなく、後で二倍角のsinの公式が必要になってくるのが面倒だけどな。 |
| webadm | 投稿日時: 2024-4-3 18:59 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
続々:直線上の点電荷と電気力線 異符号の電荷、+q, -qが2dだけ離れた点、A, B におかれているとき、ABの垂直二等分線上でABと面との交点Oから距離hの点を通過する電気力線はAからどのような方向に出るか?
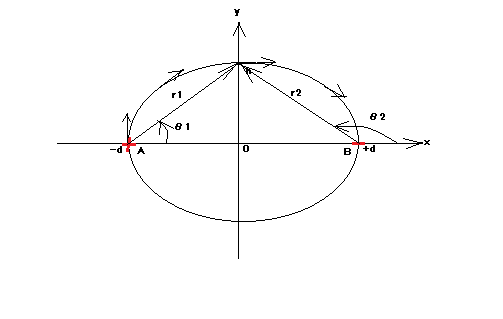 というもの。 これも前問の続きのような問題。今度は具体的に電気力線の形状について問うもの。 前問では電気力線の接線の傾き(微分係数)を導出したが、それを応用できそうである。 (2024.4.5) ふう、また寒くなってきたね( ´д`) さっきまで解答を入力してプレビューしながら内容を確認していたら、突然ブラウザーがエラーページを表示して途中まで編集していた内容が失われた罠(;´Д`) まあ昔からそういうことは時々あったけど、今回は式が途中で複雑になるので、latexのエラーと戦いながらようやく投稿しても良いかなと思える最終確認だったけど、やってしもうた(;´Д`) 再度入力しなおし。 まあ、Maximaの方には式は残っているので、それを元にまたLatexで入力し直せばいいんだけど。作業中の情熱は冷めた罠(;´Д`) なんの話だったっけ? ああ、電気力線の形状の話ね。 失われた作業を思い出して書いてみよう。 幸いにしてサーバーのmathtexのログには、作業中にレンダリングしたLatexテキストがログとして保存されていたのでそれを再利用することにしよう、一番時間がかかったのはそこだから。 前問で電気力線上の座標(x,y)近傍での微分係数が以下の形となることを得た、 これはとどのつまり電気力線の接線の傾き(tan)そのものなので、傾きをθとすると以下の関係が成り立つ。 これだと分母が0になると収束しないので、そうした特異点の無いcosかsinを使用したほうがよさげ。 上のθをcosθに代入して整理すると、 これを見ると一見複雑そうだけど、前問で用いた意図的に1で除するテクニックを使い、点電荷と電気力線上の座標(x,y)を結ぶ線分の長さをr1,r2, 線分とx軸の成す角度をθ1,θ2とすると、 つまるところ、電気力線上の電界のx成分/電界強度ということになる。ファラデーにはこれが見えていたんだろうね、数学的な知識はなくても直感的に電界の姿を電気力線として感じ取ったのは天才のなせる技と納得。 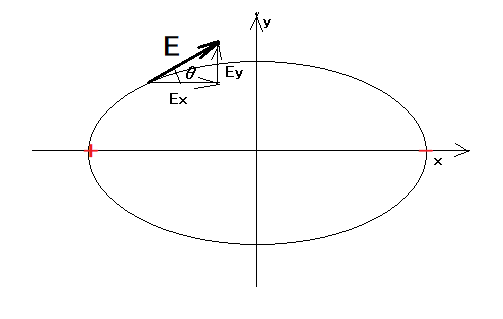 これなら電界強度が無限大になる点電荷のある座標でもcosθ=0となって、電気力線はx軸との垂線方向を向いていることが得られる。 同様に2つの点電荷の中点のy軸上の距離hの座標(0,h)では、題意の条件(点電荷が違いに異極性の場合)Ey=0となることから、|E(0,h)|=Ex となるため、cosθ=1となり、電気力線の向きはx軸に平行となることがわかる。 著者の解答を見ると、上と同じ2点の電気力線の線分の向きを割り出しているが、最後のB点に関しては触れていない。 なぜなら、B点(d, 0)では分子と分母とも0になってしまって値が収束しないため言及を避けたと思われる。 もともと点Aと点Bに関しては上下2つの電気力線の共通の始点と終点であるため、2つの電気力線上の線分の向きのy方向は互いに逆向きなので、近傍といってもどちらも含んでしまう問題がある。 この疑問を解決するのは読者の課題としよう(´∀` ) P.S 後で見直して気付いたんだが、電気力線も電界も、勾配を下る方向が正の向きなんだよな。それで電界成分が+とーで逆じゃね?と思ったんだが元々電位勾配と電界の勾配は符号が逆に定義されているので、間違いではなかったのでした。 |
| webadm | 投稿日時: 2024-3-3 22:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
続:直線上の点電荷と電気力線 x軸上の2点(-d,0,0),(d,0,0)に等量の2電荷がおかれたときの電気力線は、
で与えられることを示せ、ただし両電荷が同符号ならば+、異符号ならば-をとる。 というもの。 もちろん前問の結果を利用すれば容易いが、別のアプローチはないかね? なかなか思いつかないので、問題文の意味が正しいか実際に電気力線をMaximaを使って描画してみようじゃないかと、 (1) 2つの点電荷が互いに逆極性の場合 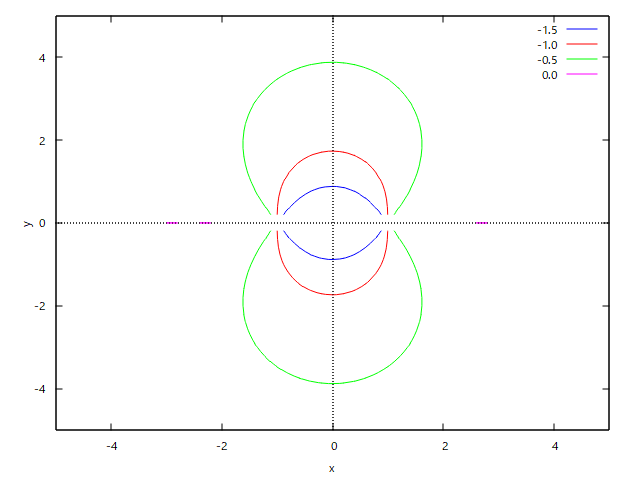 点電荷が置かれている(1,0)と(-1,0)では電気力線の式の分母が0になって計算できないので、ちょうどそこを通る力線は計算しないように描画範囲を微調整する必要があった。 互いに逆極性だと引っ張りあうので、互いの電気力線が重なりあって+極からー極へ向かう(電気力線の定義上そういう流れ)。 上はz=0のx-y平面上で見た電気力線になるが、三次元では曲面である。 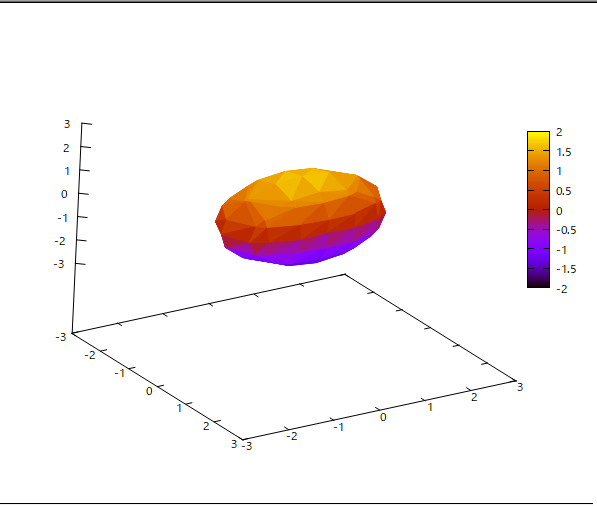 Maximaで同じ電界ベクトル場を別の方法で描画すると、 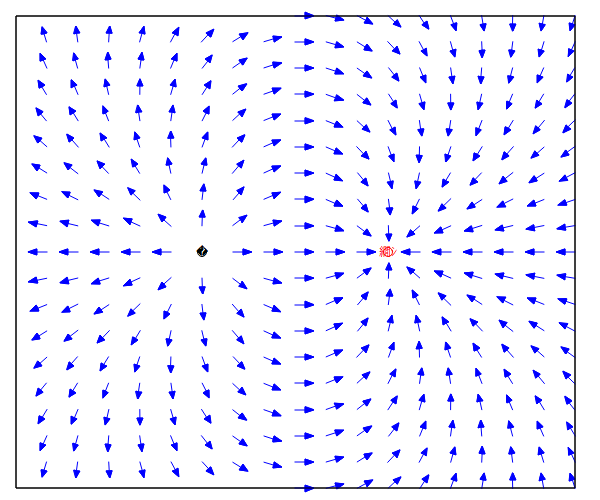 ということになり、描画されている電界ベクトルは電気力線上の接線の方向と一致してしていることがわかる。 (2) 2つの点電荷が互いに同極性の場合 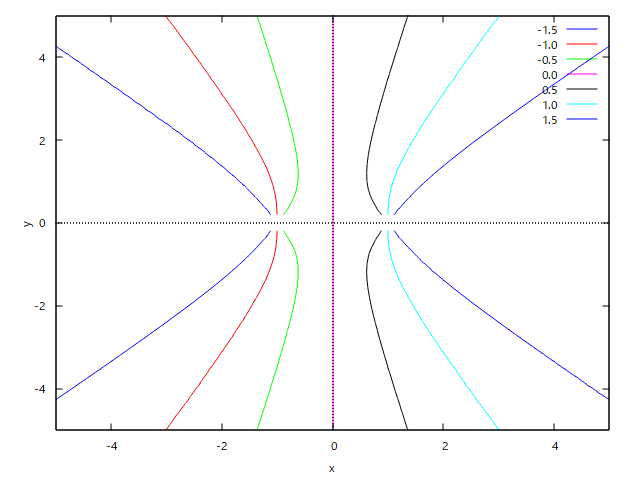 同じ極性だと反発しあうので、それぞれの電気力線は交わることなく、無限遠点に向かうのが良くわかる。 上はz=0のx-y平面上の電気力線だが、3次元では曲面になる。 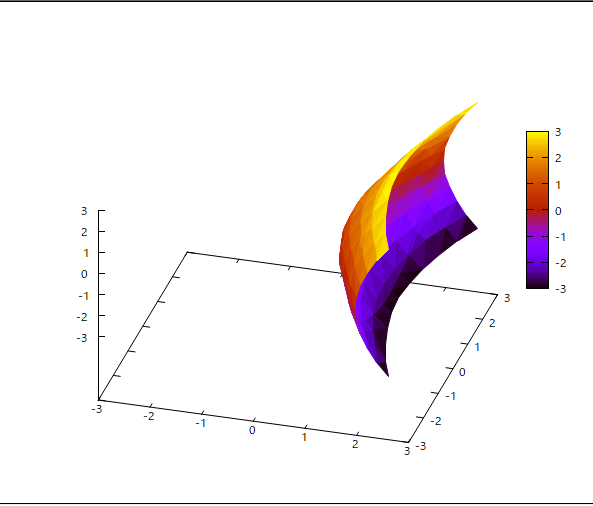 同様にMaximaでベクトル場を苦労して描画すると、 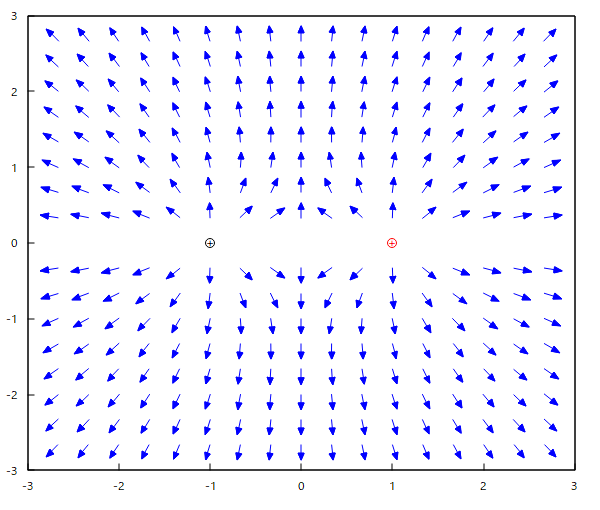 互いに同じ極性だと、縦軸と横軸で電界が0になるところがあり、そうすると正規化の際にベクトルの大きさが0になってゼロ除算が発生するので、そこだけ描画を避ける必要があった。 確かに電気力線を表しているな。 ということは解説の時に学んだ電気力線の微分方程式の解がこれだということを示せばいいんだな。 代数的な証明は後回しにして、電気力線上で接線を引くとその傾きは電界の向きと平行であることをMaximaでプロットして確かめてみよう。 さて時間稼ぎで回り道をしてきたが、そろそろ本題に取りかからないといけない。 アプローチとして思いつくのは、 (1) 一般の電気力線の微分方程式を境界条件を与えて解くと題意の式が解として得られることを示す。 (2) 等電位線の方程式を与えて、それと直交する曲線(電気力線)が満たす微分方程式を解いて題意の式が解として得られることを示す。 (3) 等電位曲面の方程式を与えて、それと直交する曲面(電束面)が満たす微分方程式を解いて題意の式が解として得られることを示す。 どちらかというと(1)が易しそうだが、(2)も電位の式は簡単なので脈はあるな。厳密には(3)なんだろうけど、難し過ぎる( ´д`) 厳密に考えると、 考え中。 題意の電気力線の方程式は、陰関数という形をしている。 多くの曲線はx座標を与えると複数のy座標を持つため、一価関数という形で表すことができないためである。 題意の式は任意の電気力線上の座標が満たす必要条件を示すことになる。 グラフを描いてわかるのは、電気力線上の任意の接線の傾きは電界ベクトルの方向と一致しているということである。 なので題意の式を微分すると電界の成分が得られるのであれば、それは電気力線の方程式の必要条件の一つを満足することになる。 更に題意の式で描かれる曲線と直交する任意の曲線は等電位線と一致することがもうひとつの必要条件である。 かなり数学上はレアで、重箱の隅みたいな議論になるので、薄い数学書では扱っていないか、とりあえず触れておくだけという参考書籍が多いのが事実である。 なので最近の電磁気学の書籍では、電気力線の議論には深入りせず、Maxwell方程式で出てくる電束密度に触れるだけで話題にもださないという傾向があるようだ。 (2024.04.02) ふう、今朝夢で一瞬答えの一歩手前まで解いた気がしたので、思い出して計算してみた。 3次元だと難しいので、z=0のx-y平面の電気力線に関する陰関数の局所微分係数が下記の電気力線の微分方程式と等価であることを示す。 題意の電気力線の方程式をz=0のx-y平面の曲線に限定して、以下のように陰関数として定義する。 電気力線上の任意の座標(x,y)近傍では、yをxの一価関数gとして扱うことができるとすると、 これをxで微分すれば、 ということになる。 これをdg/dxについて解いて、y=g(x)と置き換えれば、電気力線上の接線の傾きであるdy/dxを得ることになる。 面倒なのでMaximaで解くと、 ということになる。 上の結果の分子と分母をそれぞれ以下の式で割る(意図的に1で除する)ことで分子と分母はそれぞれ、電界のy成分とx成分となる。これが今朝の夢で見たヒント。 これはz=0のx-y平面上の電気力線の微分方程式と等価であるから、題意の式は電気力線を与えていることを示す。 やったよママン(ノД`) 3次元表現で同じことを示すのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2024-2-29 2:22 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
直線上の点電荷と電気力線 一直線上に並んだ点電荷(q1,q2,...,qn)の作る電気力線は、その上の一点と各電荷を結ぶ直線が、一直線となす角を(θ1,θ2,...,θn)とするとき、次の方程式で表されることを示せ。
というもの。 これは題意の解釈が難しいな。 電気力線は電場が存在する場所であればどこでも存在するので、電場内の任意の一点をとっても上の関係式が成り立つことを示せということだろうか? 問題文では点電荷がどのような間隔で並んでいるかも言っていないし、各電荷の極性も任意ということになる。 直線上の点電荷の作る電場は、各点電荷が作る電場の重ね合わせとして得られるが、上記の配置条件が与えられていないので直線上にあるという設定条件だけで、後は任意の定数ということで電場の式を考えるしかないな。 いまいち答えの一歩手前が見えない罠(´Д`;) 題意の式から、qiの符号は正負もありなので右辺の定数は0のケースも含まれると考えられる。 また、θiも点電荷が並ぶ直線上の点電荷が存在しない場所では、cosθiがすべて1もしくは-1となるので、その場合に題意の式が成り立つことも明らか。 残るは、直線上以外の電気力線上の任意の点においてで題意の式が成立するかを証明すること。 とりあえず、直交座標系で考えてもいいけど、点電荷は一直線上に並んでいるので、それらが作り出す電界は直線の周りで対象であるので、円筒座標系で考えると以下の様な図になる。  ここで、ω1,ω2,...,ωnはそれぞれ点電荷q1,q2,...,qnから見た直線に対して軸対象な電気力線を横切る円盤の立体角とする。 θ1,θ2,...,θnは点電荷q1,q2,...,qnからみた円盤の円周と直線の成す角度となる。 角点電荷から見た円盤上の半径rにある微少幅drの円環の微少立体角dωは、 ということになる。 従って任意の点電荷qnから円板全体を見込む立体角は ということになる。 ここでようやくcosθnなる要素が出てきたので、これがヒントだな。 さてこっからどうやって答えの一歩手前まで持っていくんだ(;´Д`) 著者の回答をチラ見すると、軸対象な同じ力線の数は距離によらず不変であることを利用している。 ならば、同じ力線の束が通る円盤の電束密度も同様に距離によらず不変であるとも言える(´ー` ) 各点電荷から出る電気力線が通る円盤上の電束密度は、各電荷から見た円盤の立体角より、 ということになる。 従ってすべての点電荷による円盤上の電束密度は、 従って、題意の関係が成り立つことが明らか。 まあ、著者の解とは電気力線の数が不変か、電束密度が不変かの違いでしかないけどな(´∀` ) 勘違いし易いのが、電束密度(electric flux density)というのは元来総電荷を含む球体表面積で割ったものなので、誘電率が関係しないのはわかる。またそれは同じ球体を通る電界に誘電率を乗じたものであることもわかるが、電気力線の数となると、電束密度を誘電率で割った値となるのが腑に落ちない点だ。それはとどの詰まり電界と等しいということか?どうやらそうらしい。 もともと電気力線は、クーロン力の強さは電気力線の数に比例するようにファラデーによって概念的に生み出されたものなので、クーロン力が強い⇒電気力線の数が多いから⇒電界が強いから、ということになる。 まあ、これで良しとしよう。 |
| webadm | 投稿日時: 2024-2-28 19:27 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
続々:静電張力 半径aの導体球を真中で折半し、もとのように重ねたものに電荷Qを与えるとき、両半球をくっつけておくのにどれだけの力が必要か?
というもの。 元の問題文にはtypoがあり、問題の意味がタダでさえわからないのに、更にわからなくしている罠(´Д`;) 今回の問題は球殻ではなく、導体の完全な球体を上下真っ二つに切断して、再度すり合わせた状態(無帯電)に電荷Qを加えると球体表面に一様に分布した電荷によって静電張力が発生し、それぞれの半球を引き離す力が発生することになる。無重力状態であることを仮定するとそれぞれの半球は静電張力が互いを引き離す方向へ働くので、ほおっておくとくっつけてあった半球は離れてしまうことが予想される。 半球を引き離そうとする静電張力の成分と逆の力を加えれば打ち消し合って半球はくっついたままになるということに。 なので、題意の意味は、2つの半球をすり合わせた球体に電荷Qを加えた場合に、半球を引き離す方向の静電張力成分を求めよ、というのと等価であると考えられる。 ようやく出発点が見えたな、先は長いが(´Д`;) 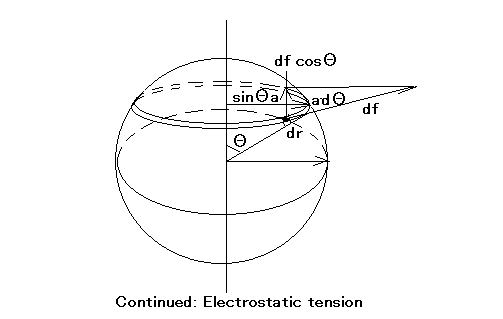 ということになる。 これは半球に関する値で、半球が2つあるので、両方でそれぞれ逆方向に同じ力を加える必要があるということになる。 著者の解答を見ると、cosΘsinΘの積分をsinΘを置換して積分しているように見える。より簡単な加法定理を使って積分しても同じ結果が得られることを確かめるのは読者の課題としよう( ´∀`) |
| webadm | 投稿日時: 2024-2-28 0:51 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
続:静電張力 半径rのシャボン玉に電気量を与えたら半径がRになった、与えられた電気量はいくらか? 表面張力をT,大気圧をp0とする。
というもの。 これも前問と同様に静電張力の問題。 前問では電位Vを与える条件だったが、今回は与えた電気量を半径の変化量から導出する問題。 前問では関係式から電気量である総電荷Qの代わりに電位Vを用いるように書き換えていたが、この問題ではその必要が無い。 前問で得られた以下の関係式の電位Vを電気量Qを使った表記に置き換えると、 ということになる。 できたじゃないか( ´∀`) |
| webadm | 投稿日時: 2024-2-26 23:43 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3094 |
静電張力 表面張力T, 半径rの帯電しないシャボン玉に、電位Vを与えたところ、シャボン玉の半径がRになったとすれば、Rとrの間にどのような関係があるのか、シャボン玉を導体と考え、大気圧をp0とする。
というもの。 シャボン玉を導体と考えるというのはおいておいて、シャボン玉ぐらいに極めて薄い導体薄膜の球体に電位Vを与えたと考えれば、なんらかの電荷に表面が帯電し、薄膜表面の微小表面電荷はそれ以外の表面の電荷によってクーロン力を受けることは解説のところで学んだ通り。 この問題では更に導体薄膜には無停電状態で予め表面張力Tと大気圧p0に抗するだけの内部圧力を持っていると考えられる。 さて、表面張力って何かね(;´Д`) そっからがスタート地点だな、残念ながら認めざるを得ないな。 調べたらかなり奥が深い罠(;´Д`) 著者の解答をチラ見したところ、表面張力Tの場合のシャボン玉内外の圧力差は4T/rと当たり前のように使ってるけど、これってどうやってそうなるの? わけわかんない罠(;´Д`) すこし、わかった( ´∀`) 広島大学の戸田先生の表面張力、表面自由エネルギーという資料に書かれている内容を参考にすると、 単位面積(幅x, 長さy)の石鹸液膜の表面張力に関して以下の関係が成り立つ ここで、wrは単位面積の石鹸液膜を長さy方向にdyだけ力Fで引っ張って広げる仕事量で、γは単位長さあたりの表面張力。2という係数は表面張力が働く石鹸液膜の裏と表があるため。 裏表で表面張力を考える必要があるところがみそな。 同じ考え方でシャボン玉のように表面張力で内外の圧力差があっても表面張力によって形状を保っている場合の球薄膜について以下の関係が成り立つ、 半径Rの球薄膜では内外の圧力差は、 ということになる。 それで4という謎の係数が出てくるわけね。 分子のdAと分母のdV1はそれぞれ約分する前に微分しないといけないのがみそだった。 これで題意の通り表面張力をTとした場合のシャボン玉の内外の圧力差は4T/rということになる。 ということで題意に即して、大気圧をp0、シャボン玉内の圧力をp、表面張力をTとすると無帯電状態では半径rを保つため以下の関係が成り立っていることになる。 ここで、電位Vを与えて帯電させることで、シャボン玉表面に一様に分布した電荷によって、静電張力が発生し、シャボン玉を膨らませる方向に力が発生し、それによって半径がRに伸びてシャボン玉内の容積が増えるためシャボン玉内の圧力が下がりp'となり、大気圧との圧力差と表面張力+静電張力が釣り合う状態に遷移すると考えられる。 静電張力は解説のときに導出したけど、電荷の面密度σで表してたと思うが、シャボン玉が膨張すると表面積が増えて面密度も下がるよな、どうすんだこれ(;´Д`) ひとひねりが必要になるぽい。 静電張力を学んだ導体の解説のところの最初に、ガウスの法則の式を面積で微分して、以下の電荷が一様に分布した表面近傍の電界強度の式を導出している。 これを利用すれば、表面積が変わってしまうと値が変わる電荷面密度σの代わりに総電荷が変わらなければ不変な電界強度で置き換えることができることに気づく。 すなわち、電位Vを与えた際に静電張力で半径がRに膨張したシャボン玉の内外の圧力差は、 あとは、表面近傍の電界強度Enを電位Vと半径Rの関係式に置き換えればいいことになる。そうすれば答えの一歩手前までくるはず。 更にひとひねりが必要だな。 シャボン玉に与えられた総電荷は変わらないので、シャボン玉表面の電界強度と電位に関して以下の関係が成り立つ。 これを先の圧力差の関係式に代入すると、 ということになる。 残るは邪魔なp,p'を消去するだけなんだが。 最後のひとひねりが必要ぽい。 理想気体の場合、膨張して体積が変化しても以下の関係が成り立つ。 という関係が成り立つことになる。 3つ4つぐらい捻りが必要だったじゃん。 これは試験には出ないな、たぶん(´д` ) 最後の理想気体の式は、後に学ぶ静電容量と電荷や電圧との関係と相似していて興味深い。 今日のコンデンサマイクはその性質を利用して、一定の電荷を蓄積したコンデンサに音圧を加えた場合の静電容量の変化をコンデンサの電位の変化に変換している。他の従来方式のマイクと比べて周波数特性に優れている。 |
| « 1 (2) 3 4 » | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

