Gan's blog - フォーラム

メイン > > 電磁気学理論おもちゃ箱 > 電気力線とGaussの定理演習問題

« 1 2 (3) 4 »

投稿者	スレッド
webadm	投稿日時: 2024-2-26 22:19
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	まだまだ：n重同心球殻半径a,b,c(a＜b＜c)の三同心導体球殻の内球と外球とを接地して中球に電荷Qを与えたとき、内球、外球上の電荷を求めよ。というもの。接地しているのに電荷が誘導されるのかという長年の疑問に答えが出す問題。問題文では電位は出てこないが、n重同心球殻の結果を応用することを意図したものであることは明らか。外球と内球は接地して電位は0になるものの、中球の電荷によって静電誘導される電荷量を求める問題となる。外球と内球は接地してあるから、電荷は無限大の面積の設置面に分布して電荷分布は0に限りなく近くなるけど、静電誘導によって電荷が生じる事実は変わらないということに。各球殻の電位は、n重同心球殻問題の結果から、 $\begin{eqnarray}<br />V_{1}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=1+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_1}\sum_{m=1}^{1}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_3}Q_{3}+\frac{1}{r_2}Q_{2}+\frac{1}{r_1}Q_{1}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{c}Q_{3}+\frac{1}{b}Q+\frac{1}{a}Q_{1}\right)\nonumber<br />\\&=&0\nonumber<br />\\V_{2}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=2+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_2}\sum_{m=1}^{2}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_3}Q_{3}+\frac{1}{r_2}\left(Q_{2}+Q_{1}\right)\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{c}Q_{3}+\frac{1}{b}\left(Q+Q_{1}\right)\right)\nonumber<br />\\V_{3}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=3+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_3}\sum_{m=1}^{3}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_3}\left(Q_{3}+Q_{2}+Q_{1}\right)\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{c}\left(Q_{3}+Q+Q_{1}\right)\right)\nonumber<br />\\&=&0\nonumber<br />\end{eqnarray}$ V1とV3の関係式を連立方程式として、Q1,Q3について解くと、 $\begin{eqnarray}<br />Q_1&=&-\left(\frac{Q\,a\,c-Q\,a\,b}{b\,c-a\,b}\right)=-Q\left(\frac{c-b}{c-a}\right)\frac{a}{b}\nonumber<br />\\Q_3&=&-\left(\frac{Q\,b-Q\,a}{b\,c-a\,b}\right)c=-Q\left(\frac{b-a}{c-a}\right)\frac{c}{b}\nonumber<br />\end{eqnarray}$ ということになる。連立方程式を解くにはmaximaを用いたのは内緒だ( ´∀｀) ちなみにこの問題も３重同心球殻コンデンサの問題と考えることもできて、中核と外殻と中核と内殻との間にそれぞれ形成される２つのコンデンサの並列接続とみなすことができ、理論的には２つのコンデンサの合成静電容量とコンデンサに蓄積される電荷総量から中核の電位を導出することが可能であると考えるが、それは読者の課題としよう( ´∀｀)

webadm	投稿日時: 2024-2-26 21:38
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	またまた：n重同心球殻半径a,bの同心導体球殻の外球殻bを接地し、内球殻aの電位をVにしたとき、両球面間の中心からrの位置の電界を求めよ。というもの。これも電位が出てくるので、先のn重同心球殻の結果を応用することを出題者は意図していることは明らか。先のn重同心球殻の結果をn=2, r1=a, r2=b, V1=Vとした場合、以下の関係が成り立つ。 $\begin{eqnarray}<br />V_{1}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=1+1}^{2}\frac{1}{r_m}Q_{m}+\frac{1}{r_1}\sum_{m=1}^{1}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_2}Q_{2}+\frac{1}{r_1}Q_{1}\right)\nonumber<br />\\&=&V\nonumber<br />\end{eqnarray}$ ここで、r1=a, r2=b, 内球の電荷Q1をQ、および外殻内面に内球の電荷で静電誘導されるQ2=-Qと置き換えてQについて解くと、 $\begin{eqnarray}<br />V&=&\frac{1}{4\,\pi\,\epsilon_0}\left(-\frac{1}{b}Q+\frac{1}{a}Q\right)\nonumber<br />\\Q&=&4\,\pi\,\epsilon_0\,V\left(\frac{a\,b}{b-a}\right)\nonumber<br />\end{eqnarray}$ ということになる。従って、外殻と内球の間の電界はガウスの法則から、 $\begin{eqnarray}<br />\oint_{S}{\bf E_{inner}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{inner}}\cdot\,{\bf n}\,dS=E_{inner}\oint_{S}dS=E_{inner}\,4\,\pi\,r^2=\frac{Q}{\epsilon_0}\nonumber<br />\\E_{inner}&=&\frac{1}{4\,\pi\,\epsilon_0\,r^2}Q\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0\,r^2}4\,\pi\,\epsilon_0\,V\left(\frac{a\,b}{b-a}\right)\nonumber<br />\\&=&\frac{V}{r^2}\left(\frac{a\,b}{b-a}\right)\nonumber<br />\end{eqnarray}$ ということになる。著者の解答には題意にはない電位の式も導いているが、この問題は後続する節で学ぶ同心導体球殻コンデンサに関する問題でもあり、その場合の静電容量Cは先の内球の電荷Qと電位Vの式より、 $\begin{eqnarray}<br />C&=&\frac{Q}{V}=4\,\pi\,\epsilon_0\left(\frac{a\,b}{b-a}\right)\nonumber<br />\end{eqnarray}$ であることがわかる。

webadm	投稿日時: 2024-2-26 21:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	続々：n重同心球殻半径a,b(a＜b)の同心球殻の外球殻に電荷Qを与え、内球殻aの電位をVにするためには、内球殻にいくらの電荷を与えればよいか？というもの。これはn重同心球殻で各球殻に既知の電荷を与えた場合の各球殻の電位を導出した結果を応用して、目的の電位にするためにどのような電荷を与えればよいかを逆に問う問題。任意のn重同心球殻の各球殻電位、 $\begin{eqnarray}<br />V_{l}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=l+1}^{n}\frac{1}{r_m}Q_{m}+\frac{1}{r_l}\sum_{m=1}^{l}Q_{m}\right)\nonumber<br />\end{eqnarray}$ ２重同心球殻の半径をr1=a, r2=bとして、外球殻の電位Q2=Qとした場合に、内球殻の電位V1=Vとするための内球殻の電荷Q1について解けばよいことになる。 $\begin{eqnarray}<br />V_{1}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=1+1}^{2}\frac{1}{r_m}Q_{m}+\frac{1}{r_1}\sum_{m=1}^{1}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_2}Q_{2}+\frac{1}{r_1}Q_{1}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{b}Q+\frac{1}{a}Q_{1}\right)=V\nonumber<br />\end{eqnarray}$ これをQ1について解くと、 $\begin{eqnarray}<br />Q_1&=&\frac{4\,\pi\,\epsilon_0\,V\,a\,b-a\,Q}{b}\nonumber<br />\\&=&a\,\left(4\,\pi\,\epsilon_0\,V-\frac{1}{b}Q\right)\nonumber<br />\end{eqnarray}$ ということになる。この結果が先のV1の式を満足することは容易に確認できる。

webadm	投稿日時: 2024-2-26 20:37
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	続：n重同心球殻全問で球殻が(1)2個のとき、(2)3個のときの結果を示せ。というもの。全問の結果である任意のn重同心球殻の各球殻電位、 $\begin{eqnarray}<br />V_{l}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=l+1}^{n}\frac{1}{r_m}Q_{m}+\frac{1}{r_l}\sum_{m=1}^{l}Q_{m}\right)\nonumber<br />\end{eqnarray}$ を使用する。 (1) n=2についてそれぞれ各球殻の電位は、 $\begin{eqnarray}<br />V_{1}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=1+1}^{2}\frac{1}{r_m}Q_{m}+\frac{1}{r_1}\sum_{m=1}^{1}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_2}Q_{2}+\frac{1}{r_1}Q_{1}\right)\nonumber<br />\\V_{2}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=2+1}^{2}\frac{1}{r_m}Q_{m}+\frac{1}{r_2}\sum_{m=1}^{2}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\frac{1}{r_2}\left(Q_{1}+Q_{2}\right)\nonumber<br />\end{eqnarray}$ (2) n=3についてそれぞれ各球殻の電位は、 $\begin{eqnarray}<br />V_{1}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=1+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_1}\sum_{m=1}^{1}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_3}Q_{3}+\frac{1}{r_2}Q_{2}+\frac{1}{r_1}Q_{1}\right)\nonumber<br />\\V_{2}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=2+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_2}\sum_{m=1}^{2}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_3}Q_{3}+\frac{1}{r_2}\left(Q_{1}+Q_{2}\right)\right)\nonumber<br />\\V_{3}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=3+1}^{3}\frac{1}{r_m}Q_{m}+\frac{1}{r_3}\sum_{m=1}^{3}Q_{m}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\frac{1}{r_3}\left(Q_{1}+Q_{2}+Q_{3}\right)\nonumber<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2024-2-23 10:25
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	n重同心球殻互いに絶縁された半径r1,r2,...,rn(r1＜r2＜...＜rn)のn個の同心球殻があり、各球殻に電荷Q1,Q2,...,Qnを与えた場合の各球殻の電位V1,V2,...,Vnを求めよ。これは最初の二重同心球殻問題を一般化したものだな。予め各球殻には最も中心に近いものから順にQ1,Q2,Q3,...,Qnの電荷が帯電していて、球殻の半径はr1,r2,r3,...,rnという具合になっている場合、 (1) 最も中心に近い球殻の内部の電界は0 (2) 球殻の隣接するすぐ外側の球殻には静電誘導によって内面には内球の逆極性の電荷が表面にはそれを打ち消す内球と同じ電荷が加わる (3)上記の連鎖で最も外側の外球には全内球に予め与えられていた電荷の総和の逆極性の電荷が、表面には全内球に予め与えられていた電荷の総和が静電誘導で加わるということになる。問題は各球殻の電位を求めよという点。電界なら各球殻表面の電荷から決定できるけど、電位はどうすんだ？　電界を積分すると無限遠点の電位が積分定数として出てきてしまうし。幸いにして一番外側の球殻が作り出す電界は表面からの距離の二乗に反比例するので無限遠の距離では電界は0となり、表面の電位は表面の電荷で決まる。一番外側の球殻の電位が既知となれば隣接する内側の球殻との電位差は内側の球殻の電荷と距離によって定まるので、外側の球殻の電位から電位差を差し引けば隣接する内側の球殻の電位となる。上記を順次内側の球殻に関して電位を計算し、最終的に中心に一番近い球殻表面の電位が求められる。それを式で整理すると、 $\begin{eqnarray}<br />\oint_{S}{\bf E_{outer}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{outer}}\cdot\,{\bf n}dS=\oint_{S}\,E_{outer}\,dS=E_{outer}\oint_{S}dS\nonumber<br />\\&=&E_{outer}\,4\,\pi\,r^2=\frac{1}{\epsilon_0}\sum_{m=1}^{n}Q_{m}\nonumber<br />\\E_{outer}&=&\frac{1}{4\,\pi\,\epsilon_0\,r^2}\sum_{m=1}^{n}Q_{m}\nonumber<br />\\V_{n}&=&-\int_{\infty}^{r_n}E_{outer}dr=-\int_{\infty}^{r_n}\frac{1}{4\,\pi\,\epsilon_0\,r^2}\sum_{m=1}^{n}Q_{m}=-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n}Q_{m}\int\frac{1}{r^2}dr\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n}Q_{m}\Big[\frac{1}{r}\Big]_{\infty}^{r_n}=\frac{1}{4\,\pi\,\epsilon_0\,r_n}\sum_{m=1}^{n}Q_{m}\nonumber<br />\\V_{n}-V_{n-1}&=&-\int_{r_{n-1}}^{r_{n}}E_{n-1}dr=-\int_{r_{n-1}}^{r_{n}}\frac{1}{4\,\pi\,\epsilon_0\,r^2}\sum_{m=1}^{n-1}Q_{m}dr=-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-1}Q_{m}\int_{r_{n-1}}^{r_{n}}\frac{1}{r^2}dr\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-1}Q_{m}\Big[\frac{1}{r}\Big]_{r_{n-1}}^{r_{n}}=\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-1}Q_{m}\left(\frac{1}{r_{n}}-\frac{1}{r_{n-1}}}\right)\nonumber<br />\\V_{n-1}&=&V_{n}-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-1}Q_{m}\left(\frac{1}{r_{n}}-\frac{1}{r_{n-1}}}\right)=\frac{1}{4\,\pi\,\epsilon_0\,r_n}\sum_{m=1}^{n}Q_{m}-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-1}Q_{m}\left(\frac{1}{r_{n}}-\frac{1}{r_{n-1}}}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_n}Q_n+\frac{1}{r_{n-1}}\sum_{m=1}^{n-1}Q_{m}\right)\nonumber<br />\end{eqnarray}$ 同じように隣接する内球殻の電位は、 $\begin{eqnarray}<br />V_{n-1}-V_{n-2}&=&-\int_{r_{n-2}}^{r_{n-1}}E_{n-2}dr=-\int_{r_{n-2}}^{r_{n-1}}\frac{1}{4\,\pi\,\epsilon_0\,r^2}\sum_{m=1}^{n-2}Q_{m}dr=-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-2}Q_{m}\int_{r_{n-2}}^{r_{n-1}}\frac{1}{r^2}dr\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-2}Q_{m}\Big[\frac{1}{r}\Big]_{r_{n-2}}^{r_{n-1}}=\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-2}Q_{m}\left(\frac{1}{r_{n-1}}-\frac{1}{r_{n-2}}}\right)\nonumber<br />\\V_{n-2}&=&V_{n-1}-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-2}Q_{m}\left(\frac{1}{r_{n-1}}-\frac{1}{r_{n-2}}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_n}Q_n+\frac{1}{r_{n-1}}\sum_{m=1}^{n-1}Q_{m}\right)-\frac{1}{4\,\pi\,\epsilon_0}\sum_{m=1}^{n-2}Q_{m}\left(\frac{1}{r_{n-1}}-\frac{1}{r_{n-2}}\right)\nonumber<br />\\&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\frac{1}{r_n}Q_n+\frac{1}{r_{n-1}}Q_{n-1}+\frac{1}{r_{n-2}}\sum_{m=1}^{n-2}Q_{m}\right)\nonumber<br />\end{eqnarray}$ ということになる。従って任意のn重同心球殻の各球殻電位は、 $\begin{eqnarray}<br />V_{l}&=&\frac{1}{4\,\pi\,\epsilon_0}\left(\sum_{m=l+1}^{n}\frac{1}{r_m}Q_{m}+\frac{1}{r_l}\sum_{m=1}^{l}Q_{m}\right)\nonumber<br />\end{eqnarray}$ ということになる。ここでは前節の電界の強さと電位の解説に出てきた、電界内の２点間の電位差の考え方、 $\begin{eqnarray}<br />V_{A}-V_{B}&=&-\int_{B}^{A}{\bf E}\cdot\,d{\bf r}\nonumber<br />\end{eqnarray}$ を思い出す必要があった。 P.S 前節を読み返すと初版と最新版とでは数式の記述が等価ながらまったく異なっていることが判明。最新版は平易な記号と表現を使用するように改訂されているのがわかる。

webadm	投稿日時: 2024-2-21 4:19
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	まだまだ：２重同心球殻前々前々問で内球を接地し、外球に+Qの電荷を与えられた場合はどうなるか？これはまた悩むな（；´Д｀）前々問とでは内球を接地したかしないかの違いでしかない。答えが同じなら問題を出す意味が無いはず、わがんね（；´Д｀）著者の解答例をのぞき見するとますますわからん（；´Д｀）どうもこの種の問題はずっと後に学ぶ静電容量の時に扱うのが普通らしい。内球を接地しない場合には外殻内の空間の電位はゼロではないものの一定のため電界が0だが、内球を接地すると内球の電位が0となって外球内面との間で外球表面の電位と同じ電位差が生じることになる。内球表面に誘導される電荷を-Q'とすると、外球内面に+Q'の電荷が、外球表面には-Q'の電荷が加わることになるため、外球外の電界は $\begin{eqnarray}<br />E_{outer}&=&\frac{Q-Q'}{4\,\pi\,\epsilon_0\,r^2},\left(r>c)\nonumber<br />\end{eqnarray}$ ということになる。外球内面と内球表面の間の電界は、 $\begin{eqnarray}<br />E_{inner}&=&-\frac{Q'}{4\,\pi\,\epsilon_0\,r^2},\left(a<r<b)\nonumber<br />\end{eqnarray}$ ということになる。従って、外球表面の電位(Vc)と外球内面の電位(Vb)は導体なので等しく、内球は接地しているため電位(Va)は0になることから内球と外球との電位差(Vab)から以下の関係が成り立つ $\begin{eqnarray}<br />V_c&=&-\int_{\infty}^{c}E_{inner}dr=\Big[\frac{Q-Q'}{4\,\pi\,\epsilon_0\,r}\Big]_{\infty}^{c}=\frac{Q-Q'}{4\,\pi\,\epsilon_0\,c}\nonumber<br />\\V_{a}&=&V_b-V_{ab}=V_c-V_{ab}\nonumber<br />\\&=&\frac{Q-Q'}{4\,\pi\,\epsilon_0\,c}-\int_{b}^{a}E_{inner}dr=\frac{Q-Q'}{4\,\pi\,\epsilon_0\,c}-\Big[\frac{Q'}{4\,\pi\,\epsilon_0\,r}\Big]_{b}^{a}\nonumber<br />\\&=&\frac{Q-Q'}{4\,\pi\,\epsilon_0\,c}-\frac{Q'}{4\,\pi\,\epsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)=0\nonumber<br />\\Q'&=&Q\frac{a\,b}{\left(b-a\right)\,c+a\,b}\nonumber<br />\end{eqnarray}$ ということになる。これを先の電界の式に代入すれば、 $\begin{eqnarray}<br />E_{outer}&=&\frac{Q}{4\,\pi\,\epsilon_0\,r^2}\left(1-\frac{a\,b}{\left(b-a\right)\,c+a\,b}\right)=\frac{Q}{4\,\pi\,\epsilon_0\,r^2}\left(\frac{\left(b-a\right)\,c}{\left(b-a\right)\,c+a\,b}\right)\nonumber<br />\\E_{inner}&=&\frac{Q}{4\,\pi\,\epsilon_0\,r^2}\frac{a\,b}{\left(b-a\right)\,c+a\,b}\nonumber<br />\end{eqnarray}$ ということになる。まあ、なんとか著者の解をなぞったんだけど、どこ参照しても帯電した内球を接地後も電荷がある程度残る理由にごにょごにょ感があるよな。外球を接地した場合には電荷も０になるのに。この種の同心球問題は試験に必ず出るぽい（´ー｀　）

webadm	投稿日時: 2024-2-21 2:09
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	またまた：２重同心球殻前々前問で外球を接地し、内球に+Qを与えた場合はどうなるか？むむ、新しく接地という概念が登場した。接地すると無限大の大地に電荷が逃げるので外殻表面の電荷分布は限りなく０になり、電界も電位も0となることになるが、内球の電荷Qによる静電誘導で外殻内側に-Q、外殻外側にQの誘電電荷が発生することは変わらない。 $\begin{eqnarray}<br />E_{outer}&=&0,\left(r>c\right)\nonumber<br />\\\oint_{S}{\bf E_{inner}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{inner}}\cdot{\bf n}dS=\oint_{S}E_{inner}\,dS=E_{inner}\,4\,\pi\,r^2=\frac{Q_1}{\epsilon_0}\nonumber<br />\\E_{inner}&=&\frac{Q}{4\,\pi\,\epsilon_0\,r^2},\left(b>r>a, Q_1=Q\right)\nonumber<br />\end{eqnarray}$ ということになる。接地とか静電誘導とか解説のときに説明しておいて欲しいよな（；´Д｀）

webadm	投稿日時: 2024-2-21 1:54
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	続々：２重同心球殻前々問で外球のみに+Qの電荷を与えた場合はどうなるか？これも続きの問題。前々問でQ1=0, Q2=Qと置換すればいいだけ。 $\begin{eqnarray}<br />\oint_{S}{\bf E_{outer}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{outer}}\cdot\,{\bf n}dS=\oint_{S}E_{outer}\,dS=E_{outer}\,4\,\pi\,r^2=\frac{Q_1+Q2}{\epsilon_0}\nonumber<br />\\E_{outer}&=&\frac{Q_1+Q_2}{4\,\pi\,\epsilon_0\,r^2}=\frac{Q}{4\,\pi\,\epsilon_0\,r^2},\left(r>c,Q_1=0,Q_2=Q\right)\nonumber<br />\\\oint_{S}{\bf E_{inner}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{inner}}\cdot{\bf n}dS=\oint_{S}E_{inner}\,dS=E_{inner}\,4\,\pi\,r^2=\frac{Q_1}{\epsilon_0}\nonumber<br />\\E_{inner}&=&\frac{Q_1}{4\,\pi\,\epsilon_0\,r^2}=0,\left(b>r>a, Q_1=0\right)\nonumber<br />\end{eqnarray}$ ということになる。ぬるぽ（´ー｀　）

webadm	投稿日時: 2024-2-21 1:47
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	続：２重同心球殻前問で内球のみに+Qの電荷を与えた場合はどうなるか？という前問の続き。前問では外球が予めQ2で帯電してあったが、それが無い場合ということになる。前問での結果で、Q1=Q,Q2=0とするだけなので、 $\begin{eqnarray}<br />\oint_{S}{\bf E_{outer}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{outer}}\cdot\,{\bf n}dS=\oint_{S}E_{outer}\,dS=E_{outer}\,4\,\pi\,r^2=\frac{Q_1+Q2}{\epsilon_0}\nonumber<br />\\E_{outer}&=&\frac{Q_1+Q_2}{4\,\pi\,\epsilon_0\,r^2}=\frac{Q}{4\,\pi\,\epsilon_0\,r^2},\left(r>c,Q_1=Q,Q_2=0\right)\nonumber<br />\\\oint_{S}{\bf E_{inner}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{inner}}\cdot{\bf n}dS=\oint_{S}E_{inner}\,dS=E_{inner}\,4\,\pi\,r^2=\frac{Q_1}{\epsilon_0}\nonumber<br />\\E_{inner}&=&\frac{Q_1}{4\,\pi\,\epsilon_0\,r^2}=\frac{Q}{4\,\pi\,\epsilon_0\,r^2},\left(b>r>a,Q_1=Q\right)\nonumber<br />\end{eqnarray}$ ということになる。ぬるぽ（´ー｀　）

webadm	投稿日時: 2024-2-20 21:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	２重同心球殻半径aの導体球を内半径b、外半径c(a＜b＜c)の導体球殻で包み、内球にはQ1,外球にQ2の電荷を与えた場合の電界を求めよ。これはキャベンディシュがクーロン力の逆二乗則を裏付ける測定実験に使われた装置にインスパイアされているのは明らか。後にマックスウェルがクーロンの逆二乗則を方程式として確定するために更に高精度な測定を更に改良された同様の実験装置で測定を行ったことが知られている。これもガウスの法則を使わないと導出が困難なので良問。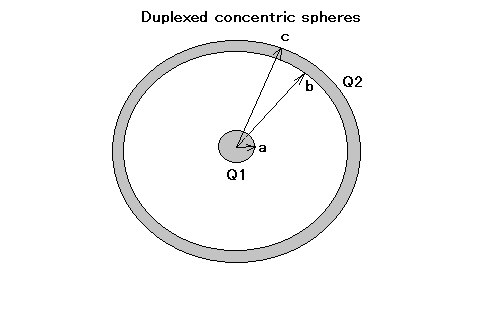この問題はガウスの法則を使うけどそれだけでは解けない。キャベンディッシュやマックスウェルがやったように、予め内球と外殻はそれぞれ別の場所でQ1とQ2に帯電させた後、ゆっくりと内球を外殻の中心に移動したと考えられる。外殻はそのために半球で開く構造になっていて、内球が中心に移動したら半球を閉じて密閉するという感じ。これによって内球の電荷Q1によって外殻の内側に静電誘導が発生し、内球と逆極性の-Q1が誘電されることになる。一方で外殻に帯電した電荷はQ2から変化してはいけないので、外殻の外側には内側に誘電されたのと逆極性のQ1の電荷が誘電される。従って内球が外殻の中心に移動して半球を閉じて球殻になった状態では、外殻表面の電荷はQ1+Q2となり、外殻内側の電荷は-Q1、内球の電荷はQ1のままということになる。これによって外殻の外から見た二重同心球殻の総電荷はQ1+Q2から変わっていないことになる。これらをまとめると、 $\begin{eqnarray}<br />\oint_{S}{\bf E_{outer}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{outer}}\cdot\,{\bf n}dS=\oint_{S}E_{outer}\,dS=E_{outer}\,4\,\pi\,r^2=\frac{Q_1+Q2}{\epsilon_0}\nonumber<br />\\E_{outer}&=&\frac{Q_1+Q_2}{4\,\pi\,\epsilon_0\,r^2},\left(r>c\right)\nonumber<br />\\\oint_{S}{\bf E_{inner}}\cdot\,d{\bf S}&=&\oint_{S}{\bf E_{inner}}\cdot{\bf n}dS=\oint_{S}E_{inner}\,dS=E_{inner}\,4\,\pi\,r^2=\frac{Q_1}{\epsilon_0}\nonumber<br />\\E_{inner}&=&\frac{Q_1}{4\,\pi\,\epsilon_0\,r^2},\left(b>r>a\right)\nonumber<br />\end{eqnarray}$ ということになる。著者は求められていない電位まで導出しているが、電位が重要になるのは、これが蓄電器として機能するという観点の場合で、まだ静電誘導や誘電体に関して解説されていないので、ここでは電界だけが問題となる。

« 1 2 (3) 4 »

スレッド表示 | 古いものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を