| ����å�ɽ�� | ��������Τ��� | ���Υȥԥå� | ���Υȥԥå� | ���� |
| ��Ƽ� | ����å� |
|---|---|
| webadm | �������: 2012-12-18 5:18 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3088 |
ʬ�������ϩ�β��ϸ��� �����Ƥ��ޤä��ǽ��ϡ�
��äȼ㤭����Heaviside������é��Ĥ�����Heaviside�Ϥ������鹹���ż����ؤ�����������櫓�Ǥ��뤬������Ϥ�����ñ�ˤϤ����ʤ����ɡ���뤳�Ȥˤ��褦�� ���Ū�ˤ�ʬ�������ϩ�β��ϸ��ݲ��Ϥ�Heaviside�ˤ�ä������줿�Τ��ǽ��������̳��Ǥ�ʬ�������ϩ�������Ϥ�����ΤäƤ����Ȥ�������Ǥ���Ω�ĵ���¿���Τǡ�����Ū�������Ϥ���Dz��ϲ��Ϥϸ�˳ؤ֤��ȤˤʤäƤ��롣 ʬ�������ϩ�������ŵ���ϩ�����ΰ��ֺǸ�ʤΤϡ����ѿ��ؿ���ʪ���̤�ɽ���ʤ���Фʤ�ʤ�����Ǥ��롣ʬ�������ϩ�������ϤǤϡ������֤Τ߰����Τǻ��֤˰�¸������ʪ���̤�ü�������Υ�δؿ��ˤʤ롣����ϴ��ÿ��ؤǽ�ʬ��������Ǥ��롣 �Ȥ������Ȥǣ��ѿ��ؿ��Ȥʤ����ʬ�Ȥ�������ʬ�Ȥ������ѿ��ؤ������Ȥʤ롣 ʬ�������ϩ�������Ϥ��Ѥ����Τ�Ʊ����ϩ��ǥ뤬���ϲ��ϤǤ���Ѥ���뤬�������ϤȰ�äƤ��줾���ʪ���̤���ϩ��ΰ��֤ȡ����֤ȤΣ��Ĥ��ѿ���ȼ�ä��ؿ���ɽ����롣 �ޤ������դ��������μ郎���ꤽ�����������ù��װƤˤʤ餺��ɬ��Ƚ��褦�ˤʤ�ȿ����ƿʤळ�Ȥˤ��褦�� |
| webadm | �������: 2012-12-18 5:22 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3088 |
�����������Ȥ��β� ���Ԥ������ϤΥڡ��������Ƥ��ʣ���ʤ��褦�ˤ��Ƥ��뤬�������ǤϤ����餤�Τ���ˡ��Ƥ���ϩ��ǥ뤫��ͤ��뤳�Ȥˤ��褦��
��������������ϩ��ñ�̶�֡ʭ�x)�ˤĤ��ƶ����ǥ��ͤ��� ñ�̶�֤�ñ��Ĺ���������ϩ����R�ȥ����������L��ľ��ˡ�ñ��Ĺ������Υ���ѥ�����C��ϳ�̥����������G���������³���줿��L����ϩ���������ΤȤߤʤ��� ñ�̶�֤κ�ü�ΰ���x�ȱ�ü�ΰ���x+��x�Ǥ���ϩ����ή���Ű��ˤϰʲ��δط�������Ω�ġ� ���줬ʬ�������ϩ�β��ϸ��ݻ��ˤ���������������Ǥ��롣 ���Ƥ��ä��餬������� �ɤ���������ä���ʡ��������� ��������Ρּ����ʳؼԤΤ���ο��س����������ǡˡפ�����ʬ�������ΤȤ������ɤ�Ǥߤ롣 z��x�����y�δؿ��Ǥ���Ȥ� ���֤��ȡ����α��ؿ�ɽ�� ����̤ˣ��Ĥ��ѿ��˴ؤ���쳬����ʬ�������Ȥ����� �¤��������ʬ��������i(t,x)��v(t,x)�Σ��Ĥ�̤�δؿ�����ʤ�ϢΩ����ʬ�������ʤΤǡ������ʤ�פ����ʤ��Ȥ�������Ϥޤ�櫓�Ǥ��롣 ���ÿ��ؤǤ�̤�δؿ����ҤȤĤ���������ʬ���������������äƤ��ʤ��� �ʤΤǤ��ä�����ϱ��ѿ��ؤ����Ƥˤʤ�櫓�ǿ��ؽ����ˤ����ʤ��ʤ롣 ���ϢΩ����ʬ��������ˤϴ��˳ؤ��Laplace�Ѵ���s�ΰ�˰ܤ��Ƥ��ޤäƹͤ�����ˡ������ޤdzؤ�Ǥ����μ��ȥ�����쥹�ˤĤʤ��ä�Ƚ��䤹�����⤷��ʤ��� �����������ơ�����Ȥϰ㤦��ƻ���ܻؤ��Ƥߤ뤳�Ȥˤ��롣 ���ȥ�ƥ����Ȥ��Ƥϡ����Ĥ��뤫�⤷��ʤ� (1) ̤�δؿ�i(t,x)��v(t,x)�����줾����Ω��������ʬ�������ˤʤ�п��ؤ��ܤ˽Ƥ�������Dz�Ϥ� (2) ̤�δؿ�i(t,x)��v(t,x)�ϸߤ��˰켡��Ω�ʤ顢�������ʬ�Ȥ���̤�δؿ��٥��ȥ��ҤȤ�������ơ�����˴ؤ���������������˽�ľ���Ʋ� ���ƤǤ��뤫�ʡ� ��Ϥ������Ȥ�������ƥ��˥å��������ˤʤäƤ��ޤä�����ʬ�������ϩ���Τ�Τ⥢���ǥ��Ȥ��Ƥ������Ȥ���������Υƥ��˥å��Ǥ���ΤǤ褤�������� (1)�ˤĤ��Ƥޤ�����Ȥ�Ǥߤ褦 �����������ؿ�ɽ���η������������ ��켰��x������ʬ��������t������ʬ����� ������̤�δؿ���Ϣ³�ǰʲ�������Ω�ĤȤ���� ��켰��������L��褸����Τ������� �Ȥ������Ȥˤʤ롣 ����˸��δ���������������R��褸����Τ������� �Ȥ������Ȥˤʤꡢv(t,x)�˴ؤ�������ʬ������������줿 �������������� �Ȥ������Ȥˤʤ롣 i(t,x)�˴ؤ���Ʊ�ͤˤ���� �������롣 v(t,x)��i(t,x)���줾�������ʬ�������ϼ¤Ϥޤä���Ʊ�����Ƥ��롣�����郎�ߤ��˰ۤʤ�ΤDz�ϼ����Ȱۤʤ뤳�Ȥ�ͽ�ۤ���롣 �긵�ˤ���Whittaker & Watson "A COURSE OF MODERN ANALYSIS"��CHAPTER XVIII "THE EQUATIONS OF MATHEMATICAL PHYSICS"�ˤϾ�μ���G=0�Ȥ��������ʲ����ͤ��ſ�������"The equation of telegraphy"�Ȥ��ƾҲ𤵤�Ƥ��롣 L,K,R�Ϥ��줾��ñ��Ĺ������Υ��������������ѥ��������»���Ǥ��롣 ���Ʊ�������긵�ˤ����������ּ����ʳؼԤΤ���ο��س����������ԡפ��ſ��������Ȥ��ƾҲ𤵤�Ƥ��롣�������γ�����ǥ����顼��ֻҤα�ư�Ҥ���Klein-Gordon��������Ʊ�����Ǥ���ȽƤ��롣 ��ǰ�ʤ���ϳ�̥�����������θ�������ˤĤ��ƤϤɤ��Ҥ�̵������������������� �����Heaviside��1876ǯ����ʸ�����������Τ�Τǡ����λ��Ϥޤ�ϳ�̥����������G����θ����Ƥʤ��ä�����1887ǯ����ʸ�Ǥϰʲ����ͤ� �����Τ���褦��ϳ�̥����������G��ޤ���ˤʤꡢ�����Τ�����������ԡ�����̵����ϩ�ξ�郎������Ƥ��롣 ���ȤϤ������ؤζ��ʽ��̤�˲Ф褤���Ȥˤʤ롣 ����������ʬ�������β�ˡ������¾��ǰ��̤�ؤ�Ǥ���Ǥϲ�ǯ��ˤʤ뤫�狼��ʤ��ʡ��������� �Ȥꤢ������ʬ�ǹͤ��ơ��狼��ʤ��Ȥ������Ф���Ĵ�٤뤳�Ȥˤ��褦�� �긵���ŵ��ز��ԡ֥���ѥ����ǡ��ŵ����إݥ��åȥ֥å��פˤ�ʬ�������ϩ�������ϤΤߤDz��ϱ������Ϥϳ䰦����Ƥ��롣¾�ˤ�Ǻܤ��ʤ���Фʤ�ʤ����Ȥ�¿�����ơ�����Ū�ˤϽ�Ȣ�ζ�Ū�Ȥʤä�ʬ�������ϩ�β��ϱ������Ϥϳع��Ǥⶵ���Ƥ��ʤ��Ȥ���������Τ��⤷��ʤ����Ĥޤ��ˤϽФʤ��ȡ� ��������Ϥꤳ���ϺǸ�ޤǴӤ��̤��٤��������� �����ܤˤ���Ƴ�Ф��줿�ſ��������ϰʲ��η���������ʬ�������ΰ��Ȥʤ롣 �Ȥ���� �����ܤǤ�s�ι��ޤ�������ʬ�������β�ˡ�㤬���Ĥ⤢�뤬���ſ��������ˤ�s�ιब¸�ߤ��ʤ������ᤸ���ʡ��������� �ʲ����ſ�������������ܤε����ȤäƱ��ؿ�ɽ�����Ƥߤ�� �Ȥ������Ȥˤʤ롣 �¤ϻ����ܤ��ɤ߿ʤ��ȡ����θ���그������������ʬ�������Ȥ����Τ��ФƤ��롣 a,b,c������Ȥ��� ��ɽ�����Τ������Ǥ��롣 �ſ����������η����˽�ľ����... ���ᤸ���쳬������ʬ�ब�ʤ������ʡ��������� ����ݡ� �����ɤ߿ʤ�ơ��裱���Ϥζ���������ΤȤ������ſ�����������ä��о줹�롣 ����ϸ��θ��꿶ư�μ� �Ȥ��ƺǽ�˽ФƤ��ơ��ſ��������Ȥ�Τ�����ȽƤ��롣 ��������ʬ�������ϩ�������Ϥλ��ˤ���äȿ��줿�Τ�פ��Ф����� �Ǥ⤳���ϳ�̥����������G=0�μ��Ǥ��롣 �����ܤǤϾ�μ��ΰ��̲�Ƴ����Ƥ��롣���������ʣ����Ĺ�����ȤʤäƤ��롣 �ޤ��Ƥ�ϳ�̥����������G���θ������Ϥ�ä�ʣ���ˤʤ뤳�Ȥ�ͽ�ۤ��ʤ��ʡ��������� �����ܤǤϤ���ʳ����ſ����������̷���������̤β�ˡ��������Ƥ��뤬�����β�����ʤ�������Ǥ����ѤǤ��롣 �ɤ����������ʡ��������� �����������ͽ���ɤ�Ǥߤ��ɽ����ˡ���ޤ��ޤ��Ǥ��ʤ����Ȥ�Ƥ��äƤⵤ���դ��ʤ����Ȥ����롣 ��Ĥ�����ʬ�����(round d)��Ȥ�ɽ����ˡ�ȡ���Ƴ�ؿ���ɽ����ˡ�����롣�ɤ����Ʊ�����Ȥ�Ƥ���Τ��������ܤϰ�äƤ��롣 �㤨�С���ϩ���Ű�V(x,t)�˴ؤ���ϳ�̥�����������θ�����ſ��������� �Ȥ����������������Ƴ�ؿ�ɽ���ˤ���� ��Ƴ�ؿ���ź�����Ϥɤ��ѿ�������ʬ������Τ����Ƥ��롣���äƴؿ�̾����ʸ��ɽ���ˤ���������ʤ��� ���������ϩ�β��ϸ��ݤξ��ˤϡ����̤�δؿ��ϻ���t�δؿ��ʤΤǡ��켡���Ǥ��뤬��ʬ�������ϩ�ξ��ˤϡ�����ü������ε�Υx���ѿ��˲ä��Τ����δؿ��Ȥʤ롣 ���ʤä��褦�˻פ��뤬�����������ϩ��Ʊ�ͤ�ʬ�������ϩ�Ǥ�Ϳ����줿�����Ф��Ƥ��β��ϱ�����ư�Ͼ�˰��а�δط������롣Ʊ�����Ϥ�Ϳ���Ƥ뤿�Ӥ˷�̤����������Ѥ��Ȥ������ȤϤʤ��ȹͤ��Ƥ褤�� �������ʬ�������β�Ȥ��ơ�V(x,t)=0�Ȥ����Τ�ͤ��Ƥߤ�ȡ�����ϲ�ΤҤȤĤȤ��Ƥ���������������� x,t���ͤˤ�餺�����ϩ�Τɤ��Ǥ⤤�ĤǤ��Ű�V��0�Ǥ���Ȥ���ȡ�v(x,t)=0���������ʬ���������������Ƥ��̤�̷�⤷�ʤ��ΤǤ����ҤȤĤβ�Ǥ��뤳�Ȥ��狼�롣 �Ĥޤ�ǽ餫���Ű������ڲä�äƤ��ʤ�����ξü��û���������֤ʤ���ϩ�Τɤ���¬�ꤷ�Ƥ��Ű�����ή�Ȥ�0�ʤΤ����������Ǥ��롣���ξ�硢�����������ϩ�ؤ��ż�ͶƳ������̵���Ȥ�������Ǥ��롢�����Ǥʤ��Ȳ�ϩ��ǥ뤬�桹����������ΤȰۤʤäƤ��ޤ��� V(x,t)=0����Ǥ���Ȥ����顢��äȰ���Ū��V(x,t)=Const.�ϲ���������� ������������Ƥߤ�ȡ�R��0,G��0�ξ��ˤ�̷�⤹��ΤDz�ǤϤʤ����Ȥˤʤ롣������R=0�⤷����G=0�ξ��ˤ�RG=0�Ȥʤ��Ȥ�������Ω�Ĥ��Ȥ����餫�� �����R=0,G=0�ξ���Ʊ���ǡ�̵»����ϩ�Ǥϼ���ü��������ü�ޤ��Ű��⤷������ή����Υ���֤ˤ�����餺����(Const)�Ȥ����������뤳�Ȥˤʤ롣 �ޤ�����Ȥ��̤�f(x,t)��g(x,t)�����줾������ʬ����������������Ǥ����硢V(x,t)=f(x,t)+g(x,t)������ʬ�����������������Ȥˤʤ롣������ſ�����������������ʬ�������Ǥ��뤫��Ǥ��롣 ������������Ƥߤ�����餫�Τ褦�˽Ť�碌������Ʊ���Ǥ��롣 �������ϩ�������ü�������ü�����ؿʤ�ʹ��Ȥ��Ű��ȼ���ü��������ü�����ؿʤ�ȿ���Ȥ��Ű������줾��f(x,t)��g(x,t)�ȹͤ��뤳�Ȥ�Ǥ��뤷������ʬ�������Τ褦�˲��ϲ������ȹͤ��뤳�Ȥ����롣 ���ϲ�ϡ�����t��̵����˰ܹԤ����0�˼�«���ʤ���Фʤ�ʤ��Τǡ����餫��t�δؿ���ؿ��Ȥ���ؿ��ؿ�E(t)��x�δؿ�X(x)���Ѥ�ɽ�����ȹͤ����롣 ����Ǥϣ��Ĥδؿ�����E(t)X(x)���ſ��������β������������������� ���ξ�硢��ʬ�λ���Ʊ�ͤ˴ؿ�����E(t)X(x)������ʬ�˴ؤ��Ƥ������������ɬ�פ����롣 �긵�ζ�Ω���ظ�������ʬ�ؤ�¿�ѿ��δؿ��ξϤ���Ƴ�ؿ���������...���餫�ʸ���������ʡ��������� ���ѡ� �����1, ¿�ѿ��δؿ�F(x1,x,2,...,xn)��xk�δؿ��ȹͤ���Ȥ� 0�ض˸°ܹԤ���Τ�n�ǤϤʤ�h�δְ㤤�Ǥ��롣 ��켡��Ƴ�ؿ���������Ƴ�ؿ�������Ӱ���Ū����m����Ƴ�ؿ��ˤĤ��ƤϾ�ά������Ϥ⤦�ΤäƤ����ϰϤǤ��롣 ������Ƴ�ؿ��δ���Ū�����ˤĤ��Ƥ����餤����� ���ѡ�
���������ΤäƤ��뤳�Ȥ������ؿ�U(x,y)����Ƴ�ؿ�Uxy,Uyx�����줾��Ϣ³������С�Uxy=Uyx�Ǥ���Ȥ����ΤȰ��Ǥ��롣 ���ˤ��褤��ؿ����Ѥ�����ʬ���������ФƤ��� ���ѡ� �������ʤΤǾ������յ�����Ƥ��ʤ�������������Ƥ���Ȥ���ȡ��ؿ����Ѥ�����ʬ�ϣ��ѿ��δؿ����Ѥ���ʬ��Ʊ�ͤǤ��뤳�Ȥ��狼�롣(1)�ΦĤ�Kronecker�ΦĤ�i=j�λ�1�Ǥ���ʳ���0�Ȥʤ�ؿ��Ǥ��롣����ʬ�����ѿ��ʳ�������ȸ��ʤ��Τ�����ʬ�����0�ˤʤ뤷�����Ǥʤ�������ʬ����1�ˤʤ�Ȥ�����̣�Ǥ��롣 ���Ƥ�������ȴؿ����Ѥ���켡����ʬ�ϡ����줾��δؿ�����켡��Ƴ�ؿ��Ȥ⤦�����δؿ����Ѥι����Ȥʤ롣�Ĥޤ���Ƴ�ؿ���ޤ��������¤Ȥ������Ȥˤʤ롣 ��������Ѥ������E(t)X(x)�ؿ����ſ������������������ �Ȥ������Ȥˤʤ롣 E(t)=0,X(x)=0�μ����ʲ������� ��E(t),X(x)�˴ؤ�������Ω�Ĥ������줬����Ω���ʤ��Ȥ��Ƥ�⤦�ҤȤĤξ�� ���������E(t)X(x)�ϲ�Ǥ���ȸ����롣 ��μ���ξ�դ��δؿ�E(t)X(x)�dz�ä���������� �Ȥ����褦���ѿ�ʬΥ��������ʬ�������������롣 R=G=0��̵»����ϩ�Υ������˸��ꤹ��Ⱥǽ�ξ��� �ȤʤꡢX(x)������⤷����x�˴ؤ���켡���Ǥ���E(t)����μ¿��ͤ�Ȥ�t�ΰ켡����ؿ��Ȥ���ؿ��ؿ��Ȥ������Ȥˤʤ롣 X(x)��E(t)������ʳ��ξ��ˤϤ⤦�ҤȤĤξ�P���� ��X(x),E(t)������������E(t)X(x)����Ȥʤ롣���ξ�郎��Ω����Τ�ξ�դ�����Ǥʤ���Фʤ�ʤ������������LC��^2�Ȥ���� �Ȥ�������ʬ�������������롣������ �Ȥ������Ȥˤʤ롣���ä�E(t)X(x)�δؿ����Ѥ�ɽ�����̵»����ϩ������������������ �Ȥ������Ȥˤʤ롣���ȤϽ������Ϳ���뤳�Ȥ�̤�그����,K1,K2,K3,K4����ꤹ��Ф褤���Ȥˤʤ롣 ����ϲ�ΰ����η������餫�ˤ����ʤ����ޤ����ξ��β��¸�ߤ�������������������Ȥ߹�碌���̵���˲�¸�ߤ��뤳�Ȥˤʤ롣���ѿ��ؿ��ξ���ʬ�������Ȱ�äơ����̲��ҤȤĤμ���ɽ���Ȥ����Τϣ��ѿ��ʾ�δؿ�������ʬ�������ˤĤ��Ƥϲ̤Ƥ��ʤ���ƻ�Ȥ����������롣 �㤨���줬����줿�Ȥ��Ƥ⡢������������ν�������ü�������Τ��������ݤʤ��Ȥˤʤꤽ���Ǥ���ʾ����ǣ��Ĥ�̤�그������ꤹ��ˤϾ��ʤ��Ȥ⣵�Ĥ�ϢΩ��������ɬ�סˡ������Ƥ�����ˡ���ɤ��Ȥϸ¤�ʤ��� �������̤����Ʋ���Ū���ü��ȥ졼�Ȥ�Ƴ����ǽ����ˡ������Τ��������Ȥ�������⤢�롣 �����κ���´�ȸ���ǣ������ǹⳬ��ή�Ρ�����ʬ�����������ɬ�פ������߷�����Dz���Ū�˲Τ������������դη����ץ�����ߥǿ��ͷ��������������롣 ������ͤ���в���Ū�˲Ƥ�Ʊ����̤�����줿���⤷��ʤ�������������Ѥ��ʤ��Ƥ�褫�ä����⤷��ʤ��ʤ���Ǥ�����Ϻ����ɬ�פǤ��롢�����Хץ����������ˡ� ���֤����Ѥ�ͤ���ȿ��ͷ��������褤���⤷��ʤ������������Ϥ�ɬ�ܤǤ��롣��������Ȥ�äѤ긷̩��ɬ�פˤʤꡢ����Ū�˲�����ɬ�פ��ФƤ��롣 ������������ʬ������������Ū�ʹͻ��ϻ��֤������뤬Ƭ������Ȥ��Ƥ������ɤ�������������Ⱦ�ˤϲʤ���ʬ��������¸�ߤ��Τ���˻�äơ�����Υƥ��˥å���Υ��ƺ���Ū������Ϥ�褦�Ȥ���ư�������س��Ƿ��깭����줿��̸��ߤ����Ū�ʿ��ؤ����Ƥ������Ū�аޤ����롣 ����������̩�˽�Ȣ�ζ���ʤ��ȡ��������������ο��ؤϤ��ʤ����������ξ��Ω�äƤ��뤳�Ȥ�Ϫ�����ƹ�¤Ū�ʳ���ؤ����Ƥ��뤳�Ȥ�;���ʤ����줿�� �ʤ���ä����ä��ä�����������ʬ�������β�͡� �ޤ��������������ʬ�������λ��ͽ�ˤ����������Τ褦���о줹�롣 ���ѡ�
�����ޤǤϣ��ѿ��ʾ�δؿ��줾����ѿ��ˤĤ��ơ�����¾���ѿ�������Ȥ�������ʬ��ǽ�Ǥ������ͤ��Ƥ������������������κ�ɸ����˱�ä���ʬ�Ǥ����ʤ������������������ʬ�������Τ��Ȥʤ���ͤ�����櫓�ǡ�����ж��֤������̤������ʬ��ͤ���ɬ�פ��ФƤ��롣 ���֤�������������ʬ��ǽ�ʤ��Ȥ�����ʬ��ǽ�Ȥ����� ���Фθ����������Ѥ���� ���ѡ�
¿��ۣ����������뤬��������ͤ��ͤ���Topology�����������äƤ������Ȥˤʤ롣 ����ʬ��ǽ�ʴؿ��Ǥ���С�����ʬ�����ѿ��ν���ˤ�餺��Ƴ�ؿ��ϰ��פ���������Ʊ���� �ճ��ˤⶦΩ������������ʬ���������˴ؤ��ƤޤȤޤäƤ���Τǡ���ʬ�������ξϤ�������ʬ�������ˤĤ��Ƥ⾯���ɤ߿ʤ�Ƥߤ褦�� �ǽ��������ʬ�������β��¸�ߤ˴ؤ��ưʲ��Τ褦�˽�Ƥ��롣 ���ѡ�
�ʤ�Τ��Ȥ����äѤ��̣�狼��ޤ��ʡ��������� ��������ʬ�������β��¸��������Ʊ�ͤˡ�������ʬ���������뤿��ν�ʬ���Ȥ������Ȥ��������� �긵��dtv-Atlas Mathematik(ˮ�� ���顼����ػ�ŵ����Ω���ǡˤ�����ʬ������������ȡ��ʲ���ʸ�̤˹Ԥ��夯�� ���ѡ�
��Ϥ���ÿ��ؤǤ�����ʬ�������ϰ���ʤ��ʰ����ʤ��ˤȤ������Τλ��¤���ǧ����롣 �������ʤ��Τǡ�̵»����ϩ�ˤĤ��Ƥ�������äȲ���������ǡ�»�����θ����ʬ�������ϩ�Ǥβ����Ƥߤ褦�� ��E(t)X(x)��ɽ�����Ȳ��ꤹ��ȡ��ǽ�ξ�P ��Maxima�Dz� �Ȥ������Ȥˤʤꡢ��� ��ɽ����뤳�Ȥˤʤ롣 �̤ξ���������E(t),X(x)�Ϥ���ä�ʣ������ξ�դ�E(t)X(x)�ǽ�������������� ���줬��Ω����ξ�դ������ʬΥ����ˤȤʤ����ͤ���ȡ������ͤ�-��^2�Ȳ��ꤹ��� ��������E(t),X(x)�������˵��夹�롣 �����Maxima�DzȤ��줾�죳�ĤΥ�������ʬ�व�� �Ȥ������Ȥˤʤ롣 �ºݤˤϾ�Τ��줾����Ȥ߹�碌�ˤʤ�櫓��E(t)X(x)�ΥХꥨ�������ϣ��̤ꤢ��Ȥ������Ȥˤʤ롣��������ǤϤʤ���Ǥ�դ�ʬΥ����ˤ���¸�ߤ������β��Ǥ�դ����¤�ޤ���Ȥ������Ȥˤʤ롣 �嵭�Ϧ�^2�������ͤ�����Ǥ�����ǿ�ưŪ�ʲ���뤬�ʤ����1887ǯ����ʸ��Heaviside�����˼����Ƥ���ˡ���ξ������硢���ʤ���̤�������ξ��ˤ������ͤ�Ȥ�R,G,L,C�˸��ꤹ����ж���Ū�ʲ�ΤߤȤʤ롣 �����Ǥ϶���Ū�˽������Ϳ�����ü�����뤳�ȤޤǤ�Ƨ�߹��ޤʤ��褦�ˤ��褦������ϱ齬�����뤳�Ȥˡ� ����ʳ��˲���������Ū����ˡ���������ꤽ�����������ͽ�˺ܤäƤ����Τϰ��̲�Ǥ褯Ƚ��ʤ��Τǡ������Ǥϸ��ڤ��ʤ��� telegraph equation�Ǹ�������ȺǤ�ʷ�ʰ��̲�Encyclopedia of Mathmatics�˼�����Ƥ��롣�ǽ��Ƴ�Ф���������ʬ��������ξ�դ�LC�ǽ����ơ� ������ ���֤��� �Ȥ��������ˤʤ롣 R=G=0��̵»����ϩ�ξ����ȡ���μ�����ư�������Ȥʤ롣 »����������ϩ�Ǥϡ���ư��������Ǯ��Ƴ�������ʳȻ��������ˤ�ξ����������ʻ�����Ĥ��Ȥˤʤ롣���Ū�ˤ�Ǯ��Ƴ���������ǽ�Ǥ�������Willam Thomson�γ����ſ������֥�Υ�ǥ�(RCʬ�������ϩ�ˤ��ͤ��Ф��졢�����Heaviside�������������ä���Ǯ��Ƴ����������ư��������ξ������������ĥ�ǥ�˳�ĥ������ ����ʬ���������������ͽ�Ǥ���ư��������Ǯ��Ƴ�������������äƤ��ʤ���Whittaker & Watson��A COURSE OF MODERN ANALYSIS��Ʊ�ͤǤ��뤬���ſ��������ϾҲ𤹤�ˤȤɤޤäƤ��롣 Encyclopedia of Mathmatics�ǾҲ𤵤�Ƥ����ˡ�ϡ�����������������˽��Ǥ����Ǥ��줿����ʻ����1000�ڡ�����ˤʤ�Courant��Hilbert�ˤ��"Methoden der mathematischen Physik:Vol 2"��Partial differential equations����Ф餷�������������椪�������Vol2�����Ƥ��������٤˺���ü�γ�ǰ��������ƥ֥�å��奢�åפ���Ƥ��ꡢ���ǤȤ��̤�Τ餷��������⤤����ǿ��Ǥ�������Ƹ��Ƥߤ뤳�Ȥˤ��褦������äȹ�ۤǤ��뤬��Vol2�����Ǥ⽽ʬ���� �����餯����¿��������ʬ���������Υͥ��ܤˤʤäƤ���Τ������Courant��Hilbert���ܤǤ������Ȼפ��롣 ��ˡ��³����������� ����ʬ�������ϩ�������Ϥdzؤ���̤ꡢ��ϩ����Ű�����ή������ü�������ü�����ذ�ư����ʹ��Ȥȼ���ü��������ü�����ذ�ư����ȿ���Ȥι�����ɽ����롣 ���������ܤ��ơ��ߤ��˿ʤ��������ۤʤ뤬���줾��Ʊ����ϩ�ˤ�ä��ȷ���Ʊ���褦���Ѳ��������Ϥ��ʤΤǡ� �ߤ�����ȿ�������˰�ư���Ƥ���ʹ��Ȥ�ȿ���Ȥ�Ʊ��κ�ɸ�Ϥ������������롣 ���֤ȤȤ�˸��ߤκ�ɸ�����Ȥΰ�ư®�٤����㤷�ƿʹ������˸�������ư�����ɸ�Τȡ��⤦�ҤȤĤϤ���Ȥޤä����������˸�������ư�����ɸ�Ǥ줾��ʲ��Τ褦��������롣 �������äƤ��ο�������ɸ��Ȥä�̤�δؿ�v(x,t)��ɽ�����Ȥ��Ǥ��롣 v(x,t)��x��t�˴ؤ����������������ʬ��ǽ�Ǥ���Ф�����Ƴ�ؿ��⿷������ɸ���Ѵ����뤳�Ȥ��Ǥ���Τ� ���äƸ�������ʬ�������ϦΤȦǤ�Ȥä� �Ƚ�ľ�����Ȥ��Ǥ��롣 ����ϰʲ��ΰ���Ū������������ʬ������ ��ʬ���A=0,C=0��B^2-AC��0���жʷ�����ʬ������(hyperbolic partial differential equation)������餷���� ���������кǽ餫���жʷ��Ƥ��뤸�������Ť��٤����ä����缺�ԡʡ��������� Ŭ�ڤ��Ѵ��ˤ�äưʲ��Τ褦�ˤʤ�餷�������⤦�����ʤäƤ뤸���ʡ��������� ���ä���ɤ�������ʡ��������� �ɤ������֤�ְ㤨�������������Encycropedia�ǤϾܤ���Ƴ�в������ھʤ��Ƥ���ΤǼ�ʬ�Ǥ�äƤߤ뤷���ʤ��� ��Ⱦ���ȼ��˶ɽ�Ū�ʲ������������E(t)�˶��̤���t�˴ؤ���켡����ؿ��Ȥ���ؿ��ؿ������ä��Τ�פ��Ф�ɬ�פ����롣�����Ǥ���С�̤�δؿ�����ˤ��η��˲��ꤷ���������Ƥߤ�Ф褤���Ȥˤʤ롣 �������������� �Ȥ������Ȥˤʤ롣�켡����Ƴ�ؿ��ιब�ü������� ���θ�Ǻ�ɸ�Ѵ�����Ф褫�ä��ΤǤ��롣 ξ�դ�4c^2�dz�ä���������� �Ȥ����ˤ��ñ��ʷ����ˤʤ롣 ������������Ū�ˤߤ��-�ˤ��ͭ�ͤȤ����ͭ�������Ǥ��롣 ������������Sturm-Liouville�������������̤ʾ��餷���������ޤǸ��Ƴؤֻ��֤����Ϥʤ��Τǡ������ޤꥳ��������é�뤳�Ȥˤ��褦��Strum-Liouville������������Ӹ�ͭ�ͤȸ�ͭ�ؿ��������ˤĤ��Ƥϡ���������ּ����ʳؼԤΤ���ο��س����������ԡפ˾ܤ����ΤǤ�����ȤΤ��ȡ� �����ǹ����ü�ʥ������Ǧ�=R/L=��=G/C�⤷����R=G=0�ξ�硢��ͭ�ͦˤ�0�Ȥʤ� �Ȥ������Ȥˤʤ롣 ̤�δؿ�U�ϦΤȦǤˤ�餺����Ǥ��뤳�Ȥˤʤ롣�����R/L=G/C��̵�Ĥ���ϩ��R=G=0��̵»����ϩ�Ǥ��Ȥ��Ĥޤ��˺ǽ�λѤΤޤ���ϩ�������뤳�Ȥ��̣���롣 ̵�Ĥ���ϩ��̵»����ϩ�Ǥϡ��ΤȦǤǾ���������������ʬ���뤳�Ȥˤ�ä�̤�δؿ�U�������� �Ȥ������ˣ��Ĥδؿ����¤�ɽ����뤳�Ȥˤʤ롣���줾�줬�ʹ��Ȥ�ȿ���ȤΦΡ��Ǥκ�ɸ�Ϥ���������������ΤǤ��롣 �����d'Alembert�β�Ȥ����Τ����ΤǤ��롣d'Alembert�ϥե�ο��ؼԤǡ��ե��ˤʼ��δ�����˼Ҹ�ͭ̾�ʸ���ƻ������Ȥ������ޤ줿������лҤǤ��뤿�ὤƻ���˼ΤƤ�콤ƻ��̾�Ǥ���d'Alembert��̾��ä������饹���ͤ����ؤ��¤���졣���θ��ȳؤdzؤ�����ؤǺ�ǽ����ʬ����ʬ�κк�����β���d'Alembert�θ�����Ϥ�Ȥ���ɴ��������ϳؤ���ؤμ�ɮ�ʤɤǸ��Ӥ����ꡢ��������������������Ȥˤ�ʤä��� ����ˤʼ��Ȥ�����ˤ�Ƥε��פʤɤ�ͽ¬�����뤿��˺���ü�β��ϳؤ�ޥ��������Ƥ�������·���Ǥ��ä����顢���ä����ޤ줿���ؤκ�ǽ���¹�������Ѥ��Τ��������⤷��ʤ���Cauchy�����϶��ܤ�ɮ�����Τ�ͥ����ˤʼ����ͤǤ�¿���������뤿��λ���������Ǥ⤢�ä�����ˤ�⤿������Ƥ�������Ȥ����ΤǤϤ���ʤΤǤ��롣ˤʼ�����ͥ��������ˤ���ܥ��Ǥ��ɤ�������Ȥ������Ȥˤʤ롣���ܷ��ξ�����ʼ�������ˤ���ƤΤ褦�˹ͤ��Ƥ����褦���������Τ����꤬���ԤˤĤʤ��ä����ɤ�����������Ĥ��Ϥޤä����ʤ��� ������������ī���ο�������Ƴ�Ԥ����餫��ˤʼ�˾ܤ����ȾҲ𤵤�Ƥ����������ΰ�̣���뤳�ȤϿ��ؤ�ʳ��μ���Ĺ���Ƥ�����ƥ�Ǥ���Ȥ������Ȥ����դ����뤿��Τ�Τ����������ʤ��ȤⲤ���ǤϤ��ΰ�̣�˼���뤳�Ȥ�տޤ�����ΤǤ������� �ʤ���ä����ä��ä���������d'Alembert�β���ä����Ȥ������ä��� �ä��ˤ�ɤ����� ̵�Ĥ���ϩ��̵»����ϩ�Τ褦�����̤ʾ��ˤĤ��Ƥ������������ǽ���äƤ��뻲�ͽ��¿�����ʤˤ�����ʤ��Ȥ�˺��Ƥ��ʤ���������ؤ���Ⱦǯ�Ǥ����դ��¾�Υơ��ޤ�ޤ�ƹֵ����ʤ��Ȥ����ʤ��Τǡ����֤ߤ�����Τ��Τ��ʤ��Ѹ��������ߤ����ʺ����ߤ����ʤ��Ȥˤʤ�Τ��פ����ʤ����� ��ۤɤ�³���˰ܤ��� ���Encycropedia�Ǥϡ���Ȥ���Riemann�ؿ��������ˤȤɤޤäƤ��롣�Ȥ�����Riemann�ؿ��äƤʤ�������ä�Ʊ���ڡ����Υ��é��Ȱʲ����ͤʻ��Ѵؿ� ����«���ʲ��������ʬ������Ω�Ĵؿ�f��¸�ߤ����礽���Riemann�ؿ��ȸƤ֤餷���� �ڡ��������λ��ͻ����ΤȤ������Τ�ʤ��̤Υ������Riemann method�Ȥ����Τ�����Τ�ȯ�����ʤ�Ǥ�������ϡ� ���˥��é��� Riemann method�Ȥ�Riemann-Volterra method�Ȥ�ƤФ��餷����Volterra����ʬ�������������о줹��Riemann method��Ʊ����ˡ����ʬ����������Ω��ȯ���������ؼԤ��� ����ϲ����Ȥ����ȡ��ſ���������ޤ����ѿ����жʷ�����ʬ�������˴ؤ���Goursat���ꤪ���Cauchy��������ˡ�Ǥ��롣Cauchy����Ͼ���ʬ�������ˤ⤢�ä����������Ǥ��롣Goursat����Ȥ����ΤϽ鼪�Ǥ��롣Goursat�Ȥ����ե�Ϳ��ؼԤ������˲��϶����˴ؤ���������Ǥ��������ο��ؼԤʤ��Τ�ʤ��ҤȤϵ�ʤ��餷���ʽ����ؼԤ������ɾ���ä����ˡ����ι����缣�����ϳ�����ɮ���Ϥ����Τ�Goursat�β��϶���������������ʪ�����ǼҤ˻���������ä�������ä��Τ������餷���� Goursat����Υ��é��Ȥ褦�䤯Riemann�ؿ���Riemann method�ʻ����ܤα����Фˤ�Riemann��ʬˡ�Ȥ����Ρˤ����Ƥ������Ƥ����� �ʲ������ѿ����жʷ�����ʬ��������ͤ��� �嵭����������������̤�δؿ�u(x,y)���ʲ�������ΰ覸��ȶ������β�����§�ǡ����ζ�����ޤ��������Ϣ³�Ǥ���Ȥ��� �����Ǧ�,�פ϶��˷����֤���ʬ��ǽ��Ǥ�դδؿ���F�����Ȥ��ζ�����ޤ�������κ�ɸ(x,y)�ˤ�����Ϣ³���ġ�Ǥ�դκ�ɸ�Ϥμ¿��ѿ�u,p,q����Ƴ�ؿ�Fu,Fp�����Fq�������ͤ������ͤ��⾮�������˸¤��¸�ߤ�����ͣ��Ǥ���Ȥ�����Ρ� �����ǰʲ�����Ʊ���жʷ�����ʬ������ �β��ɽ���Τ˰ʲ�����������������Riemann�ؿ���R(x,y;��,��)���Ѥ����롣 ��ɸ(��,��)��ax,bx,c��Ϣ³������ΰ覸���Ǥ�դ����Ȥ�����x=��,y=�Ǥˤ����� ��������R��¸�ߤ����� ��=0,��=0�ξ��Goursat����β�ϰʲ���Riemann�������Ѥ���ɽ����� �Ȥ�����Ρ��Ǥ⤳�����Ʊ���жʷ�����ʬ�������β����͡�������ˤ��Ƥ���Τ�f=0��Ʊ���жʷ�����ʬ�������β�ʤ�����ɡʡ��������� �ɤ��ߤ���Riemann method�Υڡ����θ�Ⱦ�ˤ��βƤ��ä���ʣ������ɤ����Ф��Ƥ���...orz �ʲ����жʷ�����ʬ��������ͤ��� ������Goursat�����Ʊ�ͤ˰ʲ�������ʬ��������������Riemann�ؿ���ͣ��¸�ߤ��� �����a=b=0,c=const�ξ�硢z=(x-��)(y-��)���֤��Ȱ��ѿ��ξ���ʬ������ �Ƚ����뤳�Ȥ��Ǥ��롣����˺�ɸ�Ѵ�����Bessel��ʬ������ ���Ѵ����뤳�Ȥ�տޤ��ơ�r^2=4cz���֤��� �Ǥ��뤫�餷�� �Ȥ���0����Bessel��ʬ�������˵��夹�롣���β�� �Ǥ��뤳�Ȥ��Τ��Ƥ��롣J0��0����Bessel�ؿ��Ǥ��롣���������ǻȤ��Ƥ�������ѿ��Ρ��Ǥ����t�ϡ���ɸ�Ѵ���Ƴ���������ѿ��Ȥ�̵�ط��Ǥ��뤳�Ȥ����ա���Ʊ���ʤ��褦�ˡ� ���β�ˡ�ϡ������ܤ��裱���Ϥ�14.20 Riemann��ʬˡ�α�����˽�Ƥ������Ƥͤˤ������������ܤǤϺǽ�Ū��Bessel��ʬ�������˸���������ΤȾܤ���Ƴ�в����Ͼ�ά����Ƥ���Τ����դ��Ƥ����� �ǽ�Ū�˶��{(x0,y0);(x,y)}������ʬ�������������ʬ���뤳�Ȥˤ�ä�Riemann�ؿ����Ѥ��ưʲ��η����������� ���β�ˡ��Riemann�ˤ�ä���Ƥ��줿�ΤǤ���ˤ��ʤ��Riemann method(�����ܤǤ�Riemann��ʬˡ�ˤȸƤФ�Ƥ��롣 �Ȥˤ����ſ��������β��ʣ�����Ȥ������Ȥ�Ƚ�ä��ΤǤ褷�Ȥ��褦( ����`) ������ſ����������긵�κǶᴩ�Ԥ��줿����ʬ�������λ��ͽ�ˤϽФƤ��ʤ��Τ͡� ��ˡ���������뤿��λ����������������Ѥʥڡ�������䤫�ʤ���Фʤ�ʤ�����͡������ư��̲�����줿�Ȥ��Ƥ��ü����������ΤϹ����������� �������Ƚ�ä������Ǥ���ϤǤ��롣 �ſ��������ΰ��̲�ξܤ���Ƴ�в����Ϥ����ˤϽ���ʤ��Τǡ���������ּ����ʳؼԤΤ���ο��س����������ǡפȤ����ߤ������裱���Ϥζ����������14.20 Riemann��ʬˡ�α�����Ȥ����㣲�Ǿ�����������ФƤ��롣�������Ϳ���ƶ�����������u(��,��)��Ƴ���Ȥ����ޤ���ڤ���Ƥ��롣����¾���ſ��������˴ؤ����̲����Ĥ����⤵��Ƥ��롣�ȤƤ��ɤ������Ǥ����Ǥ��롣������ˤ���Bessel�ؿ��Ƚ�������Ѥ����������Ƥ��롣 ���������а����ɤ����ǽ������β�Ҥμ�Ĺ�������κ���ʪ���¸��DZ����ʴ���ƿ�ư��ä���Ȥ�����ȿ��ǵ�§Ū�����ͤ������Τ��¬���Ƥ����ͻ������ݡ��Ȥǡ��ȼ�����ʬ�������ƤƤ�������̤�Ф�����˫����ơ��ǿ��ο��ؤǤ�Bessel�ؿ���Ȥä�����Ȥ����Τ��Ƥ��ä��Ȥ����ä���ʹ�����������餯Ʊ���褦���жʷ�����ʬ��������Goursat������ä��Τ��⤷��ʤ����ۻҤμ����¸�ߤ����ŻҤ⤢�뿶ư��Ϳ����ȷ�ޤä�ʬ�ۤ˽��ޤ�Ȥ����Τ⤢�����뤫�⤷��ʤ������äȤ������ä�������ȯŸ����¸����ä��Τ��⡣ ������Ⱦ�Υ��ץ���������ʬ�����äƤ��ޤä�������Ⱦ�Υ��ץ������Ǥ���٥��ȥ�ȱ黻��ˡ��Ȥä���ˡ���פळ�Ȥˤ��褦�� ����������Heaviside�Ϥɤ���ä��ſ��������β�����������Ѷ�̣�����뤬�������餯�ܤ���Ƴ�в����ޤǤϼ����Ƥ��ʤ����Ȥ��ưפ��������դ��� �Ĥޤ�Heavisde�����������ſ��������ΰ��̲����������ΤäƤ��������������ͤ��Ѥ��Ƥ����Ȥ������Ȥˤʤ롣������ؤǤ϶����⤷�ʤ������ʽ�Ǥ����˥��롼���Ƥ���Ȥ����Τˡ� �Ǻǽ�ˤɤ���äƵ��Τ����档�ܤ���Ƴ�в����Ͻ�Ƥ��ʤ������ʲ�����ʬ��ȡ��ɤ����1/2�٤��α黻�Ҥ��������ʬ������������̵�¤٤�����η����鸫����Ĥ����Ȥ����פ��ʤ��� ����������⺣����ؼԤ�ǧ��ʤ���ˡ�Ƿ�̤��������Ȥ������Ȥ���Ƥ��롣���Ǥ��ѿ��Ѵ��ǣ��ѿ�������ʬ���������ѿ���Bessel�������˽�ľ����Ʊ����̤�����Τ�ʪ�����ؤξ�����ʤǤ��롣 ����ʾ����ϻߤ�ơ��������˼�ʬ�ǹͤ��Ƥߤ褦�� �٥��ȥ�ȱ黻�Ҥ���Ѥ��뤿��ˤϡ�����ޤdzؤ�Ǥ������Ȥʤ�ȿ������ɬ�פ����롣�����ľή��ϩ����ʬ�������ϩ�������Ϥޤǡ��ع��ǤϤ���ʻ��֤Ϥʤ��ΤǤ��ä����꼰�����줿��Τ�ͤ���ळ�Ȥˤʤ뤬��������ȿ�����Ƽ�ʬ�ǹͤ��������褤�˷�ޤäƤ��롣������������ȿʤ߶��˸Ŀͺ����礭���ǤƤ��ޤäƤۤ�ΰ찮��οͰʳ�������ȤʤäƤ��ޤ��� �ع��⾦����������褵��ƻߤ�Ƥ��ޤäƤϼ��פ������Τǡ��ʤ�Ȥ����褷�ʤ��褦�˹��פ���Ⱥ����Τ褦�ʴѸ��Х��������դ�����ι�Ԥߤ����ʷ��ˤʤäƤ��ޤ��� �ǽ�˽��褦������ʬ�������˴ؤ��Ʒ���Ū�˳ؤ֤����ǿ�ǯ�Ϥ����äƤ��ޤ��������Ƥ�������ʬ�Ϥ�����μ���ȤϤ���Υ�줿��Τ��� �ǽ�˲����ſ��������ΰ��̲����Τ�����Ȥ�������Ϥ�ۤ����褤���⤷��ʤ������줬���������ϩ�β��ϸ��ݤȤɤ��㤦�Τ��⡣ ����Ū�ˤ������ȯü����ͤ��Ƥ����Τ����̤������դ˲������������ظ����äƹͤ���Ȥ������ץ�����������Ϥ������ɤ��⸫�����ʤ��� �㤨�С�̵��Ĺ��̵»����ϩ������ü�˥��ƥå������Ű���ä������β��ͤ��Ƥߤ�ȡ�̵»���ʤΤ�������ϩ��οʹ��Ȥ��ȷ��������ȤΤޤޤȤ������Ȥˤʤ롣���������ü��̵�±����ˤ���Τ�ȿ���Ȥϱʱ�ˤ�äƤ��ʤ��Τ���ϩ��Ͽʹ��ȤΤߤȤʤ롣 ���ñ��˻��֤ȶ�����ϩ������ü�����˰�ư�����Ű�1�Υ��ƥå״ؿ��Ȥ������Ȥˤʤ롣�������֤�����ü����ε�Υ���ɸ���Ȥ���ʿ�̾�˿�ľ���Ű���ץ��åȤ���ȡ� �Ȥ����Ϥ�ڤ�Τ褦��Ω��ɽ�̤��Ȥ�����뤳�ȤΤʤ��ΰ�λ��ѷ���ʿ�̤�Ĥʤ�ʻ�����褦�ʶ���̤Ȥ������Ȥˤʤ롣 v(x,t)�ϣ��ѿ��ΰ���ؿ��ʤΤǸ�̩�ˤ���ʿ�̾�κ�ɸ���飱�����κ�ɸ�ؤμ����ˤʤ롣���Ƥ��β����ϴؿ���ɽ�����Ȥ��Ǥ���Τ��������������ʤ����ݤ����ʤ��Ȥ��ưפˤ狼�롣 �㤨�л���t��t0�˸��ꤷ��x�˴ؤ���v(x,t0)��ץ��åȤ���� �Ȥ�������Ȥˤʤ롣�����Fourier����Ƕ�����褽���Ǥ��롣 Ʊ�ͤ�x��x0�˸��ꤷ��t���Ѳ����������� ����������ȤʤΤ�Fourier�����ɽ�������Ǥ��롣 ���������ʿ�̤�����ɽ���ˤϤɤ�����Ф����Τ������� ��Ϥ����ˤʤꤽ����ͽ�ۤϤĤ�������ʾ�ϸ������Ĥ��ʤ��� �ޤ�x,t�����줫���������Ȥ������δؿ���Ƴ�ؿ��Ϥɤ��ʤ�Τ��������������ʬŪ�ˤ�Ϣ³�Ǥ��뤫�顢����ι�����ʬ����ǽ���⤷��ʤ�������������ʾ�Τ��ȤϤ狼��ʤ��� �ɤ���ʿ�̾����(x,t)����v(x,t)�ؤμ����������ݤǤ��뤫�顢���ä��Τ���(v(x,t),i(x,t))�Ȥ���ʿ�̤ؤμ�����ͤ����ۤ����褤�ΤǤϤʤ����Ȥ����ͤ����⤫�֡� ���֤��ȴ����������ϱ黻�Ҥ��Ѥ��� U�����ʳ��δؿ��Ǥ����硢�黻��F����ĵդǤʤ���Фʤ�ʤ����� �Ȥ����ط�������Ω�Ĥ��Ȥˤʤ롣 �����ˤ⤽��餷�����������뤬������餬�����̣����Τ����鸫�̤��Ƥ��ʤ��� �ͤ�ľ������ �ɤ�����Ⱦ�η�̤��ſ�����������ʬ�黻�Ҥ��Τ�ΤǤ��롣�Ĥޤ��ſ��������ϴ������������������������ä��Τ����ſ��������Υ��쥬��Ȥ�Ƴ����ˡ��������Ĥ��Ƥ��ޤä��������� ��ή���Ű��δؿ��٥��ȥ�ǹͤ���ȡ����̵��Ĺ̵»����ϩ�β�϶ˤ��ñ���ɽ�����Ȥ��Ǥ��롣 ����ʿ�̾��(x,t)�Ϥ��κ�ɸ�ˤ�ä���ή���Ű��Υ٥��ȥ���֤�ʿ�̾�Σ����Τɤ���˼�������뤫��ޤ뤳�Ȥˤʤ롣�ʤ�ۤɤ����������ĵդʤ櫓�Ǥ��롣(x,t)��Ϳ������Ű�����ή�����Ū�˵�ޤ뤬�����εդϽ���ʤ���������ñ�ͤǤ����ͤǤϤʤ�����Ǥ��롣 ��������ȴ����������ǤϤʤ����������������Ǥ����ſ����������Τ�Τ��ɬ�פ��ФƤ��롣�������֤���������������� �Ȥ������Ȥˤʤ롣 ������U����Ⱦ���ȼ���Ƴ�����ɽ�Ū�ʲ�η���������������ǰʲ����ͤ��֤�������� �쳬�ιब�ä��� �Ȥ������Ȥˤʤ롣 ���������=��=0��̵»����ϩ�ˤ⤷���Ϧ�=�¡�̵�Ĥ���ϩ�ˤξ�� �Ȥʤꡢ��ư�������Ȥʤ뤳�Ȥ��狼�롣 ���Τ��Ȥ�̵�Ĥ���ϩ�ξ������Ѥ������楱���֥���õ���дꤷ�Ƥ���Heaviside�����˾��κѤߤǤ��롣 ������ʬ�ε�������˾Ҳ𤷤�Courant&Hilbert�������192�ڡ������о줹�롣��˾Ҳ𤷤������ܤ˽Ƥ���Riemann��ʬˡ�ˤ���ˡ��Goursat�������153�ڡ����˸����������Ȥ��Ǥ����������ˤϽ�ŵ��1894ǯ�Υե�ο��ؼ�Picard�ʥԥ�����)����ʸ�Ǥ���ȵ����˵�����Ƥ��롣Goursat�Ϥ���������Τ��Ƥ���ǿ��β��ϳؤ����̤�ɴ������Ū�ˤޤȤ�夲�������Ǥ��뤬�������κ���ü�ο��ؼԤ��鸫��Ȥɤ���ŵŪ���Ƥ��ä��Ȥ����櫓�Ǥ��롣���줬���ܤǤϻ����ܤ���˼����Ѥ���Ƥ���櫓�ǡ�ʣ���ʿ����Ǥ��롣�����缣��Goursat������˰쵳�Ǥ����٤����ϳ�����ɮ������ΤΡ�Ʊ������¤ˤʤä����������������缣��������ɤ�С��ֲ桹�����ܿͿ��ؼԡˤǿ������ܤ���Ǥ��٤�������Ƥ���ΤǤϡפȶĤ�˰㤤�ʤ���Topology�˴�Ť������ϳؤϴ��˳����ǤϤ����Ĥ����Ǥ���Ƥ��뤬�����ܤǤϸ�ŵŪ�ʤ�Τ�����������ʤ�����Ϥ�ع��Ƕ�����ˤ�Topology���������ФȤʤäƤ��ޤäơ���ŵŪ�ʶ������Τۤ����ƤäȤ��ᤤ���餫�⤷��ʤ�������������ʬ����ɾ�Τ���L.V.Ahlfors��COMPLEX ANALYSIS 3/e���ˤȤä��ɤ�Ǥߤ�����Topology���ФƤ����Ȥ����Ǻ��ޤ���������������H.Legesugue����ʸ���ɤ���Ȥ����äѤʤ���Topology��Ƚ�äƤ��ʤ��ȤĤ��Ƥ����ʤ��ΤǺ��ޤ�������ä��� �ʤ���ä����ä��� ���Ƥ��褤���κ������������ΰ��̲��黻��ˡ�Dz��Ȥˤ��褦�� �Ƚ��Ȥ����ǻפ��Ф����Τ������黻��ˡ�η����Ϻ���������������˽������Ϳ���������̤��ޤޤ�Ƥ��ʤ��Ȥ����ʤ����Ǥ��롣�Ĥޤ�黻��ˡ��¾�β�ˡ�Ȱ�äư��̲��Ƴ���Ƥ���������Ϳ����̤����ʬ�������ꤹ��Ȥ������Ȥ��Ǥ��ʤ��Τǡ��ǽ餫����ʬ�����ޤ�Ǥ���ɬ�פ�����Τ��ä��� �黻��ˡ��Ĥ��鷺�˥������ɥå���������Ʊ����ʬ�������β�ˡ���Ѥ���е�Υx�˴ؤ���ɽ�Ū�ʰ��̲������뤬��������ɼԤβ���Ȥ��ơ������Ǥϱ黻��ˡ��Ű���롣 �Ť��黻��ˡ�ˤ��ʬ�������ϩ�β��ϲ��ϤˤĤ��ƽƤ����ܤ�ȡ���Ϥ�黻��p=��/��x�˴ؤ�����˾���ʬ����������ˡ�Dzơ�q=��/��t��������ư����ˤ���˴ؤ��ƽ������Ŭ�Ѥ���q����ꤹ��Ȥ������ȤƤ��뤬���ɤ���褯Ƚ��ʤ��� �Ԥ��ͤޤä��Τǡ�Heaviside����ʸ��Electrical Papers Vol I��ǽ餫��į��Ƥ����顢�����֤��ʲ��Τ褦�ʵ��Ҥ��ۤʤ���ʸ�ʤȤ�������Phi Mag���Ϣ�ܡˤ˷����֤��ФƤ��롣 ��Ǽ�ʬ�Ǽ��ư�����Ƥʤ��äƤߤ뤳�Ȥˤ��뤬�ʲ��η�̤�������Ȥ��롣�����Fourier���ǽ���Ѥ�����ˡ���Ƚ�Ƥ��롣 �ʤ���黻��ˡ�ǵ��櫓����ʤ��Τ�( ����`) ����äȸ��β٤����ꤿ��ʬ�� Electrical Papers Vol II���ɤ߿ʤ��ȡ�192�ڡ�����"Section XL. Preliminary to Investigations concerning Long Distance Telephony and Connected Matters"��Heaviside��W. Thomson�γ��쥱���֥�˴ؤ���RC��ϩ�����˿�ȯ����Ʒ���Ƥ���Ƴ�Τμ���ͶƳ��ʬ��ϳ�̥����������ä��������Τ����ſ��������Υ����ǥ������߽Ф����аޤ���Ƥ��롣Ʊ����W.Thomson�η�̤�̵��Ƚ�ˤ��Τޤ��Ͼ���ſ���ϩ��ή�Ѥ�����ʸ���Mr. Preece���٤Ȥʤ������������Ƥ��롣����ʳ�����ʸ�ʻ����Ϣ�ܡˤǤ⣱�ڡ�����˲��٤Ȥʤ�Mr. Preece��̾�����о줷��Ƚ�βв֤餷�Ƥ��롣 �ޤ�Electrical Papers Vol II��Ⱦʬ�ޤ�į������������̶ХХ��ιԤ�����κݤ˹ͤ�³������̡��黻��ˡ�Dz����ʵ������Ƥ����� �ޤ������������ϩ�λ���Ʊ���褦�ˡ����κ���������������ʬ���ƽ�����ˤ�äƷ�ޤ륷���ƥ�������̤Ȥ��Ƥ�̤����ʬ���(�٥��ȥ�ݥƥ��ˤ�и������롣�ſ��������ξ�硢���֤ȵ�Υ�˴ؤ��Ƥ��줾������ʬ�ब����Τǡ��ǽ�˵�Υ�˴ؤ���������ʬ���롣 �黻��ˡ�ξ�硢��ʬ����ʬ�黻��p�εձ黻��1/p��褸������ǺѤࡣ�����٥��ȥ�V�ˤĤ��Ʋ� �Ȼפä��鵭����ʬ�̾�¤�ã���Ƥ��ޤä��Τǡ��ե�����������³������Ȥˤ��褦�� |
| webadm | �������: 2013-2-15 8:37 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3088 |
Re: �����������Ȥ��β� ɽ��Υ���åɤ�³����
�ȵ�Υx�˴ؤ��Ƥ����롣 �黻��ˡ���������������ͥ�줿���ϡ���κǽ��������Ū�˸��̤������Ǥ��롣 ξ�դ��Ȥΰ�ư®�٤Ǥ���c������褸��ȡ��ݥƥ�륨�ͥ륮���������Ȥʤ롣�Ĥޤ�����ü�������ü��������ã�������ϩ��Υ��ͥ륮���̤�ɽ�����Ȥˤʤ롣e=mc^2�κ�����դˤ����褦�ʴ����Ǥ��롣 �Ȥ���ȥݥƥ��٥��ȥ�K1�Ͻ�����ͥ륮���̤ǡ�K0����ϩ��Υ��ͥ륮����ư�̤Ǥ��뤳�Ȥ������狼�롣 ����ʤ��Ȥ�ͤ��Ƥ���ȡ��⤦�ҤȤĤθ�����ͭ�뤳�Ȥ˵��Ť��� �ʹ��Ȥ�ȿ���Ȥ�®ƻϩ���Ф겼��μ������ư���뼫ư�֤���ȹͤ���ȡ��Ƽ�ư�֤Ϥʤ�餫�Υ��ͥ륮������äƤ��뤳�Ȥˤʤ롣ȿ���Ȥ��ʤ���С����ͥ륮����®��c����ϩ���Ʃ���Ƥ���������ü������ϩ�˶��뤵��륨�ͥ륮���ϻ��֤ȶ������ä��롣 ���ݤʤΤǺǽ��ȿ�ͤ�ͤ��ʤ��ƺѤ�̵��Ĺ��ϩ�ǹͤ�������ȿ�ͤ�����Ȥ���ȡ����������饨�ͥ륮���ΰ����⤷������������äƤ��뤳�Ȥˤʤ롣̵»����ϩ�Ǥʤ����ˤϹ�����ϩ��ǥ��ͥ륮�������ͤ���Ƽ�����Τǡ���Υ�ȶ��˸��ꤷ�Ƥ����� �ʤΤǤ��ʤ���̷���ͤ���Ȥ�䤳�������Ȥˤʤ�Τ��狼�롣 ���Ƽ��ϻ��֤˴ؤ��Ʋ�ɬ�פ����롣���줬������� �ޤ��ʲ����Ѵ���Ԥ� �ɤ���������ä���ʡ��������� ���ʤꤪ��夲�ξ��֤ʤΤǡ�Heaviside�Τ⤦�ҤȤĤ�����Ǥ���"ELECTROMAGNETIC THEORY"�λ�����Τ����黻��ˡ�ˤĤ��Ʋ��⤷�Ƥ���Vol II���ɤ�Ǥߤ��� ��Ⱦ�Ϥ���Ȥ����뽸�������ϩ�ؤα黻��ˡ�ˤ����ʬ�������β�ˡ�������³����ʬ�������ϩ�Τ����������䶭�����˴ؤ�������ʬ�������β�ˡ�ؤα��Ѥ��Ҥ٤��Ƥ��뤬���ۤȤ�ɷѤ��ܤʤ��Dz��⤵��Ƥ���Τǡ������ɤ�Τ˶�ϫ���롣�Τꤿ���Τ�ʬ�������ϩ�Τ���������������˻Ȥ��Ƥ��뵭��Ȥ��������äȤ�������ΤȤ������������Ƥ����Τ��ä��ꤹ��Τǡ�����̤ä��ɤ�ɬ�פ����롣 ������Heaviside�Ȥ����ɤ�ʬ�������ϩ������ʬ�������˴ؤ��Ƥϵ�Υ�˴ؤ��Ʋƻ��֤˴ؤ��Ƥ���ʬ�黻�Ҥ��Ĥä��ޤޤκ������������ξ��֤β�ˤĤ����͡��ʽ������ͻ����Ƥ��롣�����ΰ�˴ؤ��ƲΤϸ�Ⱦ�ǹԤ��Ƥ����� Heaviside�ϻ����ΰ�˴ؤ��Ʋ��ʳ��ǡ��ɤ����Ƥ������Ǥ�դδؿ�������Ƥ��Ƥ��ޤ��Τǡ��ȼ��ˣ��Ĥ�̵�¤٤������ɽ���Ƥ����������椫���ä��ɤ��Τ��Ƥ��룲���Bessel�ؿ���Ȥä��ۤ����ɤ�Ƚ�Ǥ��ơ�Bessel�ؿ���Ȥä�ɽ���˽�ľ���Ƥ��롣 318�ڡ����ˤۤȤ�ɤ����餬Ƴ�����Τ�Ʊ��������������ΤĤ����Ȥ��ˤ��ܤä����ʤ���ɤ��Ȥ����ޤǤ��äƤ��ʤ���( ����`) 1/2�٤����ʸ����������������Ǥ��ޤäƤ��뤬��p���/��t�ǦҤϡ������ꤺ�äȰ�����218�ڡ����˰ʲ��Τ褦���������Ƥ��롣v��1/LC��ʿ�������Ȥ���ã®��c��Ʊ�ͤǤ��롣�ڡ����κǽ�μ��ȣ����ܤμ�����٤��cosh����ʬ�ǡ�p����)�Ȥ��Ƥ���Τ��ɤ��狼��ʤ����ж����ؿ���ɽ���⺣�Ȥϰ�äƤ��롣cosh��Ʊ������sinh��shin�Ȥ���ɽ�����Ȥ��Ƥ��롣Heaviside�Ϥ�����黻�ҤΤ褦�˰��äƤ���ΤǤޤ�Ƚ��ˤ����� �����ΤȤ����Ǧ�=0�ξ��ˤ�̵�Ĥ���ϩ�ˤʤ�ݤ����⤵��Ƥ��롣R����ϩ��ľ����L��ľ���������K����ϩ��ϳ�̥����������S����ϩ�Υ���ѥ����Ǥ��롣Heaviside������Ǥ�C��Current�ΰ�̣����ή�Ȥ����Ѥ����Ƥ���ΤǺǽ�ϸ��Ǥ����⤷��ʤ��� �����餬Ƴ��������Heaviside�μ�����٤�ȡ��������Ť��Ƥ��������٥��ȥ�ݥƥ��K0,K1�Ϥɤ�������t�δؿ��٥��ȥ�Ȳ�᤹�٤��褦����������Υx������ʬ������0�ˤʤ�Τ�����ξ��ȡ�����t�δؿ��ξ�礬�ͤ����뤫�����x������ʬ������ˤϻ���t������ȸ��ʤ��Τ�0�ˤʤäƤ��ޤ������Τ��Ȥ��θ������ư���³����ˡ��ͤ��Ƥߤ褦�� ����ˤ��Ƥ�Heaviside��Electromagnetic Theory�ˤ�̵�¤٤����������Ǥ⤫���о줹�롣̵�¤٤�������餱�Ȥ��ä��ۤ������������⤷��ʤ��� ����Ǥ�ή�Ф�Heaviside��é�ä��Ƥξ�ƻ���õ�빥���ԤϤ��ʤ����⤷��ʤ�����������Heaviside��������ɤ�Ǥ���ȡ��ޤ����Ԥ�©���������롣t=0�ǤΥ���ǥ�ή�����ή�ε�ư��ͻ����Ƥ��뤢����Ǥϡ����餫�˸�ŵʪ���ؤθ³�����ָ���Ȥ����ޤǶ�Ť��Ƥ��봶�������롣����������Υߥ����ʹͻ����̻Ҥ�������ͤ��ʤ����������Ǥ��ʤ������������������̣�Ǥϡ����ޥ��奢���ż����ؤ��ŵʪ���ؤο��Τ����̻�ʪ���ؤι�ߤؤ�ä����ФäƤ��Τ�Heaviside��¸�ߤ���ߤˤʤ뤫�⤷��ʤ����ޥ���Ū�ˤϤɤ��Ǥ�褤�������Ȼפ��Ȥ����ޤǼ�ٹ�˸��ˤ�褦�Ȥ��Ƥ��롣 ����Electromagnetic Theory���ɤ߿ʤ���396�ڡ�����ʣ�������ʼ����пԤ������Ȥ����ǡ���ñ�ʽ��������ϩ��Heaviside�黻�Ҥ�Ȥä���������������³����Heavisde�ζ�س�ι����֤��Ƥ���Τ�ȯ�������� Heaviside���ȤϤ���ޤǤ��ſ������֥�������Electromagnetic Theory��ɮ���룲��ǯ���˼���ȤϤᡢ�䤬��Maxwell�μ���ͶƳ������W.Thomson�γ����ſ������֥���������Ĥʤ��뤳�Ȥ˵��Ť������椬ͭ��®�٤�����뤳�ȡ�Fourier�β���Ω�������̵�µ���ˤʤ뤳�Ȥ��Τꡢ����ǯ�ܤˤ��Ƥ�ä�ͭ��Ĺ��ϩ�ν�ü��û���������ȳ�������������ϤǤ����ȿʹ֤���ߤ��ߤ�����Ƥ��롣���θ�Σ���ǯ�֤ǡ����Ƥζ������ˤĤ��ơ�ʣ���ʤ٤������ѤǤ��뤬�ʲ���392-393�ڡ����δʷ�ʷ��ˤޤȤ�뤳�Ȥ��Ǥ����������餯�ְ㤤�Ǥ����Ƥ��뤫�⤷��ʤ������⤷�����Ǥ����������餯��������褦�ȽҤ٤Ƥ��롣 ���줬Heaviside���ǽ�Ū�������ſ��������ΰ��̲�Ǥ��롣 ���θ�ˤ�ºݤβ���������Ū�˼�������ˡ��ʹ��Ȥ�ȿ���Ȥ�����ϩ���ʤ��Ű�����ή���ɤ��Ѳ����뤫��դǿ����Ƥ��롣����Ϻ����Ǥ��¬��������ϩ��ο������¤��ͻҤ������λ���˷����ƥ���դȤ��ƥץ��åȤ����Ȥ����Τ϶ä��٤����ȤǤ��롣 ��ǯ�ǺѤ��ä�����ʤ��Τ͡ʡ��������� �ޤ������ŵ���ϩ�����������Ȣ����˳��Ϥ��ƣ�ǯ�ˤʤ뤷�����ʤ�������ǯ�䣲��ǯ�Ȥ����Τϴְ㤤�ǤϤʤ��褦�ʵ������롣�ȳؤ��Ȳ��ƻ�Ȥ����ƻ�Ȥ��¤�ƻ���������뤷�� ���ޤ����ȼ��Τ������Heaviside��������ƻ���ڤä�����������¾�ˤ�ä�Heaviside�����ǵ�ʤ��ä����¤�����Τǡ�����������Ĵ�٤Ƥߤ褦�� ��Υx�Ȼ���t�˴ؤ��Ƥɤ��餫����˲Ƥ�褤�褦�ʵ������뤬��Heaviside�⤽���Ƥɤ�Laplace�Ѵ���Ȥä���ˡ��ܤ��Ƥ���ƥ����Ȥ�ǽ�˵�Υ�˴ؤ��Ʋơ��Ǹ�˻��֤˴ؤ��ƲƤ��롣 �դ��ä�������ɤ�ʷ�̤�������Τ��������� �ޤ��ǽ��������ʬ����������֤ˤĤ��ƲƤߤ�� ���֤���ʬ���Ƶ�Υx�˴ؤ���Ǥ�դδؿ���и������� �����V�ˤĤ��Ʋ� �Ȥ������Ȥˤʤ롣��Υ����˲��ΤȻ����褦�ʴ����ˤʤä�����������ˤ���1/2�٤��α黻�Ҥ��ФƤ��Ƥ��ޤ��Τ����ʤ��� �Ȥ������ȤǸ������������é�äƤ⤳�������踱�����Τϰ����� Heaviside�⣲��ǯ�����ܤ�դ餺�˲��Ϥ�����̤ˤ��ƤϺǸ�ϼ��Ȥʤ����Ǥ��롣�黻��ˡ�DzΤ�����̵���Ȥ����Ĥġ���Ⱦ���ִ��˼����ִ���Ϣ³�Ǥɤ��ˤ���Ԥμ��ˤͤ�������Ȥ����������ݤ�ʤ����ºݤˤ�̵�µ�����Ѥ�̵�µ���Ȥ���ʣ���������̤�ʤ��Ȥ������Ȥ����餫�ˡ� Telegraph equation�Ǹ�������ȡ����⿷������ˡ���ſ���������Ȥ����ơ��ޤ���ʸ�ˤʤäƤ��뤰�餤�ʤΤǸŤ�����������Ǥ��뤳�Ȥ��Ѥ��ʤ������Ͳ��ϼ�ˡ���͡���ߤ��Ƥ��뤬���Ǹ�ϸ�̩��ʲ��ϲ�ˤȤθ���ʬ�Ϥʤ���Фʤ餺����Ϥ����Ū�˸��̤��褯�Ȥ������פ����롣�ʤΤǡ��ſ��������β��ϲ���Τϳع��Ǥ�̵���ʴ����⤷�ʤ��Ǥ�ʤ�������ä�¸�ߤ��ΤäƤ������٤ǡ����ɬ�פˤʤä����ٶ���ľ���Ȥ����Τ��ɤ��Τ��⤷��ʤ��� �����¤��ξ��¤˸�����äơ��ǽ�δ����������Υ٥��ȥ�ɽ������ꡢ�����Ǥ�Ϥ���ʬ��ȤäƤߤ褦�� U�ˤĤ��Ʋ� �Ȥ������Ȥˤʤ롣����Ϥޤ��ѿ�ʬΥ���ˤ������δ������������ʳ����������ˤ��θ�ɤ��ʤ뤫��ͽ�ۤ��Ĥ������ʴ��������롣�ж����ؿ����ФƤ��Ƥ���Τǡ� Heaviside�ϵ�Υ�ˤĤ��Ƥ����Ƥޤ�������ʬ�˴ؤ���黻�Ҥ��Ĥä����֤Ǵ�ñ�ʽ����狼��Ϥᡢ������Ƥξ��ˤĤ��Ʋ����Ƥ��롣���̲��Ȥ����ΤϺǸ�ˤޤȤ�Ȥ��ƹԤä������Ǥ��롣����Ū�ˤϺǽ�˽������Ϳ���Ʋ�ΥХꥨ��������ʤ����Ǥ��ä��ۤ��������פ����� �����Ǥ�Heaviside���������¤�ʤ��뤳�ȤϤ��ʤ��ǡ�����Ū�ʻ������鸫�̤����ɤ���ˡ�������Ƥߤ뤳�Ȥˤ��롣 ;�̤�����Heaviside�α黻��ˡ��ޤȤ�Ƥ�����ؽ�Ȥ����Τ������Ĥ�¸�ߤ��롣�ҤȤĤ����̾Ҳ𤷤�Courant&Hilbert��"Methods of Mathematical Phisics Volume 2"��"TRANSIENT PROBLEMS AND HEAVISIDE CALCULUS"�ˤ���p517����Ϥޤ�"��2 The Heaviside Methods of Operators"�Ǥ��롣���ξϤǤϿ���Ū�ʾ����Ȥ��ϻ���ʸ���Ȥ���Mikusinski��"Operational calculus"����α��Ƥ��롣 ��ʬ�黻��p�Ȥ��εձ黻��1/p���Ĵ��ˤʤ�Τ�������Ǵؿ�g(0)=0�Ȥʤ�������Ǥ���Ȥ��ä����Ƥ��롣����ϰ����ˤʤ�ɤ��Ƥ����̤ꡢHeaviside�α黻�Ҥ�������Ǵؿ��ˤϸ����ʤ�Heaviside�Υ��ƥå״ؿ�����˾褸���Ƥ���ȹͤ����Ǽ�����롣 (2013/03/01) ��Ω�Ρֿ��ظ�����������פα黻��ˡ�Ѵ�ɽ���ʤ��롼�ڤdz��礷�Ƹ��Ƥ����顢�ʲ����Ѵ��Ф��Ǵ������ˤ���Τ�ȯ�� �ǽ��Ƴ������Ȥ��ä��ꤸ��ʤ���( ����`) ��̯�˰㤦���ɡʡ��������� ��ä�Bessel�ؿ��ȤΤĤʤ��꤬�����Ƥ����� (2013/3/21) ��μ��ϱ黻�ҹब�����Ĥ���Ѥ��ޤޤ��Τǡ�ñ��˹ͤ��Ƥ���߹�����ʬ�Ȥ������Ťˤ�Ÿ�������Τ��������ʤ�����Ϥꤤ���ʤ���̲��ΤϿ����ʽ�����Фʤ��ȤǤ��ʤ��Τǡ���ä��ü�ʥ���������˲Ƥߤ�Τ��褵�����Ǥ��롣 �ޤ��ǽ�˺Ǥ��ñ��̵»����ϩ��̵�Ĥ���ϩ�ˤĤ��ƲƤߤ�Τ��Ȥˤ��롣̵»����ϩ��̵�Ĥ���ϩ�ǤϦ�-�¤ι�Ͼü�����Τ� (2013/3/28) �٥��ȥ�ݥƥ��K0,K1����t�˴ؤ���ؿ��Ǥ����ǽ�����ͤ����뤿����㤨������ü�˸�ή�Ű����ä�������ˡ�����������Ͻ���������餫�ˤ��ƥ������Х��������Dz�ɬ�פ����롣 �ǽ��Ⱦ̵��Ĺ�ʼ���ü�ޤǤε�Υ������ü������Ȥ��Ϥ��ʤ�����ʬĹ���ˤ���̵»����ϩ��ͤ���� ������x0��x0��0�ǽ�ʬ�礭���Ȥ��롣 �������������ȥ٥��ȥ�ݥƥ��˴ؤ���ϢΩ�������������� �����٥��ȥ�ݥƥ��K0,K1�ˤĤ��Ʋ� �Ȥ������Ȥˤʤ롣 ����������μ������������ �Ȥ������Ȥˤʤ롣 ������x0��̵����˰ܹԤ���� �Ǥ��뤫�餷�ơ�Ⱦ̵��Ĺ��ϩ�ξ��ˤ����ब�ü��� �Ȥ������Ȥˤʤ롣 �黻���������ǤϾ��ξ�դ�Heaviside�Υ��ƥå״ؿ����褸���Ƥ���Τ�Taylor�������ˤ�� �Ȥ������Ȥˤʤ롣 ����Ϻǽ�˥���դ�ץ��åȤ���ͽ�ۤ�����̤Ȱ��פ��Ƥ��롣 �ʤ���黻��ˡ�Dz뤸��ʤ���( ����`) Heaviside�ϲ��Τ�����ˡ��פ��Ĥ��ʤ��ä��Τ��������� ̵»����ϩ�Ǥ�R=G=0�Ǥ���Τǡ���μ��Ϻǽ�Ū����ϩ���Ű�����ή����ʬ�Ȥ���٥��ȥ�U���������ʤ롣 Ⱦ̵��Ĺ��̵�Ĥ���ϩ�ξ��ˤϡ����˰����̤ä��������������ʳ�����Ƴ��ɬ�פ����� ������Υ�˴ؤ��ƣ�����ʬ���٥��ȥ�ݥƥ���и�������� �����U�˴ؤ��Ʋ� ����˰ʲ��ν������Ϳ���ƥ٥��ȥ�ݥƥ��K0,K1��� �������������������� ������x0��̵����˰ܹԤ�������ब�ü��� �Ȥ������Ȥˤʤ롣����ü����ε�Υ�ˤ�äƸ����ȷ��ο��������ꤷ�Ƥ������Ȥ��Τ����줿�� ���Ƥ��������褬�������ͭ��Ĺ��ϩ�ξ��ˤ���Ƴ�����������������˼���ü�ν�ü��郎�ۤʤ륱�����ˤĤ��Ƥ�Ʊ�ͤǤ��롣�Ĥ��Ǥ���ϩ�μ���ͶƳ���θ���Ƥ��ʤ�Thomson�Υ�ǥ�β��Ƴ�����Ȥ��Ǥ������������ �ǽ��RCʬ�������ϩ(Thomson�γ��쥱���֥��ǥ�ˤˤĤ��ƹͤ��Ƥߤ褦�� RCʬ�������ϩ�Ǥ�L=G=0�Ȥʤ�Τǡ�����ޤ�Ƴ�Ф������Ǥ�ʬ�줬0�ˤʤäƤ��ޤ��ޤ������Ȥˤʤ�Τǡ����ܤ�Ω���֤�ɬ�פ����롣 ������������������������Ω������ ������L=G=0���֤��� �Ȥ������Ȥˤʤꡢ�ſ��������ϰʲ����ͤ�Ǯ��Ƴ�������Ȥʤ� ������Υ�ǣ�����ʬ���ƥ٥��ȥ�ݥƥ��K0,K1��и�������� �����U�ˤĤ��Ʋ� �Ȥ������Ȥˤʤ롣 ������Ⱦ̵����ϩ������ü���Ű�E����Ĥ�������� ��Ϳ���ƥ٥��ȥ�ݥƥ��K0,K1�˴ؤ��Ʋ� �������������������� �����Ⱦ̵��Ĺ��ϩ�Τ���x0��̵����˰ܹԤ���� ���Ƥ������ܳ�Ū�˱黻��q��1/2�٤��褬�ФƤ��Ƥ��ޤä��� ��������� �Ȥ����Ѵ��Ф����Ѥ��뤳�Ȥˤ��롣 �Ȥ������Ȥˤʤ롣 erf�ϸ����ؿ��� ���η�̤��顢��ϩ��ή�����ή������ü����ε�Υ���������㤷�Ƹ��ꤷ�Ƥ������Ȥ�Thomson����Ŧ�����쥱���֥뤬��ˤ����ʤ��ʼ���ü��ã����������ϩ��ή�����˸¤�ʤ���Ť��Ƥ��ޤ�����ͳ�Ȥ����� ��ή�μ���C=0.12uF/mile, R=1k��/mile�Ȥ��ƥץ��åȤȤ��Ƥߤ�� �Ű��μ���Ʊ�����ǥץ��åȤȤ��Ƥߤ�� 100mile�������λ��֤��Ф����Ѳ������ή�Ϥ����˥ԡ��������줿�帺�ꤹ������ʤΤ��Ф��ơ��Ű��ϻؿ��ؿ�Ū�����ä�������Ǥ���Ȥ��������ʰ㤤�������롣 (2013/3/31) ���ޤǻȤäƤ���Maxima�ΥС�����Ť��Ƹ����ؿ����ץ��åȤǤ��ʤ��ä����ǿ���Maxima�ȡ��뤷���Ȥ����տޤ����̤�˥ץ��åȤǤ���褦�ˤʤä����褦�䤯PAUL J. NAHIN��"Oliver Heaviside"��page 33�ΰʲ��Υ���դ���٤뤳�Ȥ��Ǥ���褦�ˤʤä��� ����ü����ε�Υ����бۤɡ���ή�����ꤷ�Ѳ��������ˤʤ롣Thomson�Ϥ��Τ�����ϩ�����ͤ��뤿��β��ɤ����Ϥ����� ��������Ǥʤ�RCʬ�������ϩ��ǥ�ǤϳȻ���ǥ�Τ��΅�椬�Ϥ����֤���Υ��Υ����Υ���ۤ��٤��ʤ�Ȥ����ſ��ˤ��Թ礬���������⼨����̤Ȥʤä��� ������Heaviside���������饤�ѥ������줿�Τ�Ʊ�ͤ˶ä��٤����̤��ä���������Ū�ˤߤ������ü������ϩ������Ƥ����δ֤��ǤĤʤ��äƤ���Τǡ��ɤ�ʤ˱Ǥ�����ü�˲ä���줿����Ͻֻ�����ϩ������Ƥ�������ʬ������Ƹ����Ȥ������Ȥ��̣����ʤ���������Υԡ����������®�٤�����ͭ�¡ˡ�������ŵ����椬ͭ�¤�®�٤Ǥ��������ʤ��Ȥ��������ξQ���鸫��ȥʥǤ��롣�����ޤǤ����Ǥ����ʤ��� Heaviside����ϩ�μ���ͶƳ��ʬ���θ�����ſ����������������Ȥˤ�äƿ��椬�Ĥ�̵�������®�٤Ǽ���ü��������郎���뤳�Ȥ�ǧ���줿�Τ����äλ���ˤʤäƤ���Τ��ȤǤ��ä��� ����Ⱦ̵��Ĺ��ϩ�ˤĤ��Ƥϥͥ����Ԥ����Ȥ�����ͭ��Ĺ��ϩ�˲��Ϥ����뤳�Ȥˤ��褦�� �������˰���Ⱦ̵��Ĺ�ΰ��̤�ʬ�������ϩ�ˤĤ��Ʋ��Ϥ��Ƥ�������¾�ˤ�G����ȴ������ΤȤ�L����ȴ������ϩ���ͤ����뤬�����褦�ʤ�ΤʤΤǡ� �ǽ��Ω���֤ä� ������Υ�ǣ�����ʬ���ƥ٥��ȥ�ݥƥ��K0,K1��и�������� �����U�ˤĤ��Ʋ� �Ȥ������Ȥˤʤ롣 �ʲ��ν������Ϳ���ƥ٥��ȥ�ݥƥ��K0,K1��� �����μ�����������x0��̵����˶˸°ܹԤ���� �����Ȥ����ޤǤ������ɡ��������餬�Ӥθ����ꡣ ���η�̤�����˲��ϺѤߤ�Ⱦ̵��Ĺ��̵»����ϩ��̵�Ĥ���ϩ��RCʬ����ϩ�ξ��(��Ŭ�Ѥ�����������̤������뤳�Ȥ��餳�μ����Ȥ��������äƤ��ʤ����Ȥ��Τ���뤳�Ȥ��Ǥ��롣 �ɤ���������ä���ʡ��������� ��μ��ϰʲ����ͤ˽����뤳�Ȥ��Ǥ��� (2013/4/1) �Ű��β�Ϥޤ������ɡ���ή�β��������̵�Ĥ���ϩ�ξ���=�¤�Ŭ�Ѥ������˲��ϺѤߤ�̵�Ĥ���ϩ�β��Ʊ����̤������뤳�Ȥ��ǧ�� E=1,R=1,G=0,C=1,L=1����ή��ץ��åȤ���� 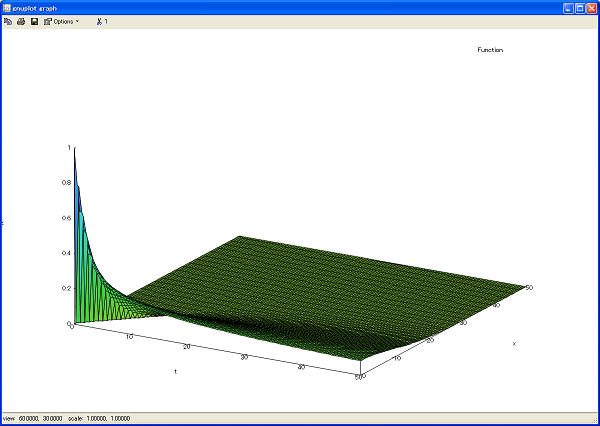 (2013/5/5) ���Ƴ�в����˸��꤬���ä��Τǽ����������٥���դ�ץ��åȤ��Ƥߤ��Ȥ�������Ϥ�Ĥޤ�ʤ���̤ˤʤäƤ��ޤä������֤ηв�ȤȤ����ή�ϸ�����������ü������֤ۤ���ή�⾯�ʤ��Ȥ������������η�̤Ǥ��롣�Ȥ϶��־�ˤ���ּ���ˤ⸽��ʤ��� (2013/4/6) �Ű��β�ϰ����ǤϤ����ʤ������ʤ�μ����Ƨ�ޤʤ��Ȥ����ʤ�����������Ū�˵��Ÿ�����ƥҥ�Ȥ�����ɬ�פ�����Τ��������������Ȥ����ʤ��ʤ�����������Ⱥǽ�Ū�ˤ�Bessel�ؿ����ФƤ���Ϥ��ʤΤǡ�Bessel�ؿ��ˤĤ��Ƥ���������Ƥ���ɬ�פ����롣��ή�β�������������Ω����ä��Ű��β������Ȥ�����ˡ�⤢�뤬������Ϥ�äƲ�ä���ˡ�˻פ���Τǥ��ȥ졼�ȤȤϸ����� ��Υ���դξ�����ϳ��»�������ʤ���Τ���ϩ»�����礭������˿��椬���Ϥ�������ʤ����Ȥ����餫���������꤬Ϫ�������Τ��ſ��������äλ���ˤʤäƤ���Ǥ��롣Heaviside���ſ��������β餽�Τ��Ȥ�ͽ�����Ƥ��β�������ͰƤ��õ���дꤷ�Ƥ������������ϩ�μ��ʥ�������������䤻�С���ϩ������˰տ�Ū���礭�ʥ�������������٥�������������뤳�Ȥǡ�Ʊ����ϩ»���Ǥ�椬���ޤ��Ϥ��Ȥ�����ΤǤ��롣 �ºݾ�Υ���դξ���L������2�ܤˤ��ƥץ��åȤ��Ƥߤ�� ����ȿ��Τ������äơʿ��椬�ޤ��Ϥ��ˡ����椬����뻰�ѷ��ΤϤ�ڤϤä���ȸ����Ƥ��롣 ���������Ū�ˤ�Heaviside���õ������������������뤳�ȤϤʤ��ä�����ĥ�����������õ��������ϰϤ�1%����뤳�Ȥʤ��ä����ᡢ�õ�����������ظ����碌�Ƥ��ޤä�����Ǥ��롣 �������������Τ褦��Ʊ�������֥뤬���쿮�����¤ˤ��ޤ������뤿������Ѥ���Ƥ��뤬�������ȯ�������Τ�Heaviside�Ǥ��롣 (2013/5/8) �����Ȥ����Ű��β��é��Ĥ��ʤ��Ǥ��뤬�������ˤ��������Ĥ��ơ���Ϥ�ǽ�˸��Ĥ���Bessel�ؿ��˴ؤ���黻��ˡ���Ѵ����������ȯ����Τ��褵�������ȵ��Ť�������Ω�ο��ظ����ˤ��ޤ��Ť�Heaviside�α黻��ˡ����Ƥ����Ѵ�ɽ��˭�٤˷Ǻܤ���Ƥ���Ȥ����Τ���å������ä���������ǽ��Ƴ�����Τ�ï���Ͻ�ŵ��ʪ�����ڽ�Ƥ��ʤ��Ȥ������½�������ܤι������⤢�äƤ�����ʾ忼�ɤ�����櫓�ˤ⤤���ʤ��� �ǽ�˸��Ĥ����Ѵ�������ξ�դȤ�Ǥ���ʬ����ȡ��ؿ��ؿ��μ����ˤ���黻�Ҵؿ����ä��롣 �Ű��μ��Ǥ�n=0�˳�������Τ���������� ���Ȥϱ��դ��Ѵ�����Ф��������Ǥ��뤬�����ä��餬���� �Ȥ������Ȥˤʤ롣 �ºݤ��Ű��μ��Ǥϻ����٤����ǤȤ��⤢�äƣ��Ĥδؿ����Ѥ���ʬ���Υx����ʬ����Ȥ������Ȥˤʤ롣���ݤʤΤ�Maxima�Ƿ������������Τ����ब��Υ�δؿ��ˤʤ�Ȥ����Τ����� �嵭�β������˸����ſ��������β�Ǥ��뤫�ɤ�����Τ����Τ��ɼԤβ���Ȥ��褦( ����`) ���ꥸ�ʥ��Heaviside�α黻��ˡ���ſ�����������Ȥ������Ȥ�Ƚ�ä������Ǥ���ϤǤ��롣�����Ϥ��Τ��餤�ˤ��Ƥ��褤��Ǵ��α齬����ˤȤ꤫���뤳�Ȥˤ��褦�� P.S �ɼԤ���ˤ��Ű��β�Υ���դ��ץ��åȤ�����Τȴ��Ԥ���Ƥ������⤤�����⤷��ʤ�������ǰ�ʤ�����ή�β�Ȱ�ä�Bessel�ؿ���ޤ���ʬ�बG=0�ξ��Ǥ�Ĥ뤿�ᡢ����̤˵���������¶��־�ˤϥץ��åȤǤ��ʤ��ΤǤ��롣���Τ��Ȥ���ή�β�Ǥ�G��0�ξ��˵���������G=0�ξ��Ǥ���ʬ�ऽ�Τ�Τ��ü�����Τǡ����ξ��ǥץ��åȤ����Τ��ä�����ʬ��μ¿��ͤϰ��Ĥ����Ű�E�Ȥ��ơ�E���ϰ���˼�«���뤳�Ȥ����餫������Bessel�ؿ����Τ�Τ�ñ��ʲ��ϴؿ��ǤϤʤ���̵�¤٤�����Ȥ����ü�ʴؿ��Ǥ��뤿����ʬ����¿��ʻ��֤��פ��뤷��t��x/c���դ�������������ˤ���������ʬ�ͤ˲ä��Τ���ʬ�ͤ��Τ�Τ�ʣ�ǿ��ˤʤäƤ��ޤ�������������Ϻ�����ޤ�̤�������Ȥ��ƻĤ롣�ʤΤ��ſ��������β���꼰���Ͻ���Ƥ⡢���η���̤���˽���ʤ��Ȥ����Τ������Ǥ��롣Heaviside�Ϥɤ���äƣ��������ˤ��β��ץ��åȤ������Ȥ����Τ�����Ȥ��ƻĤ뤬���ɤ����̵�¤٤��������«�������ˤ�Ʒ����Ƥ����餷���������Ǥ�ʤ��ȼ���Ǥ�¿��ʻ��֤ȷ����٤��п�ɽ��Ȥ��ʾ塢����ۤ�ͭ�������˾��ʤ����餽��Ϥ���Ǥ褫�ä��ΤǤ��롣��������β����ɼԤμ�ͳ����Ȥ��褦( ����`) ���ͤޤǤ����������ʬ�ؿ�����������֤ǥץ��åȤ��Ƥߤ���Τ��ʲ����̤� ����������(��=x)���դ������ܤ��ФƤ���Τϡ������ΰ��sqrt(tau^2-x^2)���������ˤ�������ˤʤäƤ��ޤ�ʣ�Ƕ��֤˼̤äƤ��ޤäƥץ��åȤǤ��ʤ����ᡣt=0���դ��礭���ͤ�Ȥ�Τǡ���ʬ�ऽ�Τ�Τ�̵�뤹��櫓�ˤ⤤���ʤ��� ���٤��ϰϳ���(tau - x) < 0���⤷���� (tau^2 - x^2 ) < 0�ξ��ˤϴؿ��ͤ���Ū��0�Ȥ��Ƥߤ���� �����Ȥ��ƻ����������ն�������ܤ�����롣ʣ�ǿ����������ˤ�äƸ���Ƥ��ޤäƤ��롣���ȤϷ�̤�ʣ�ǿ��ʤ鶯��Ū��0�Ȥ���Maxima�ε�ˡ������в���Ǥ��뤫�⤷��ʤ��� (2013/5/15) �ɤ��ͤ����顢�ץ��åȤ���ʤ��Τϡ���-x��0���ϰϤ�����ʬ�ؿ��ͤ�ʣ�ǿ��ˤʤ�Τȡ��ӡ�0�������ͤˤʤ뤫����ä��ʡ��������� �������Ȥ�����äƤ�����ü���ξ������ɡ������Ǥ��ͤ�����ˤʤ�Ȥ���櫤�...����ѥ��Ȥ���ʤ��Τ͡� (2013/5/17) �褯�ͤ�����켡��Bessel�ؿ��ϴ�ؿ����ä���t-(x/c)=0�ξ�������ʬ�ؿ���0��Ȥ�ȹͤ��Ƥ褵������ʬ��μ�����ʬ�Ҥμ�������̵�¤٤�����ʤΤ�t^2-(x/c)^2��1�ξ���0�˶�Ť��� ����ʬ�ؿ����̤������ܤ��Ǥ��ʤ��褦�ˤϤǤ������ɡ���ʬ����Ⱦ������Ѥ�餺���⤷��������ʬ�����Ǥ��ʤ��Ȥ��ʤΤ��ʡ������Ű�ʬ�ۤη��ȥץ��åȤ��ɼԤβ���Ȥ��褦( ����`) P.S �������Ф餯�����Ƥ��ʤ��ä�������ҤΡ���ز������ŵ���ϩ�ʣ��ˡ����ꡡ������ߤ��顢Laplace�Ѵ���Ȥäƺǽ�Ū�˰ʲ��Τ褦�ˤޤä���Ʊ����̤�������ȽƤ��ä������Ǥˤʤä��ܤβ��Ʊ����̤������Ƥ�Miksinsky�ȵ��Ļ�ˤϿ������ʤ������������ʤ��Τǡ��ޤ����ǤˤʤäƤʤ����Ҥ����ܤ�Ʊ����̤��ȳ�ǧ�Ǥ��ư¿�����������Ǥ�ä���̲��롣  ��ʬŪ�˰�äƤߤ���Τϵ����������ۤʤ�Τȡ�����ε���ο���Ǿ������Ƥ��뤿��ǡ��ºݤϤޤä�����Ʊ�ͤǤ��롣�����٤�Τ���ñ�̥��ƥå״ؿ�u(t)��褸�뤳�ȤDz����ʬ�����ƽ�ɬ�פ�ʤ��Ȥ������ȤǤ��롣������̵�Ĥ���ϩ����̵»����ϩ����Ŭ�Ѥ���Ȥ����δ��Τβ��Ʊ����̤�������Τǰ������äƤ��ʤ����Ȥ�Τ���뤳�Ȥ��Ǥ��롣�������� |
| ����å�ɽ�� | ��������Τ��� | ���Υȥԥå� | ���Υȥԥå� | �ȥå� |
| ��Ƥ���ˤϤޤ���Ͽ�� | |

