| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2024-5-3 22:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
帯電した楕円体導体から生じる等電位面 帯電した楕円体導体から生じる電界の等電位面は焦点を同じくする楕円体面になることを示せ。
というもの。 これも数学的でラスボス級だな(´Д`;) だが挑戦してみるテスト まずもって疑問から、 (1) 楕円体って何? 楕円ってなんだっけ? (2) 楕円体の焦点って何? 楕円の焦点は知っているけど。 まずは(1)だけど、立体の断面のどこを切断しても楕円になるのが楕円体ということになる。球も特殊な楕円体ということになる。 特殊な楕円体には球を含め、回転楕円体というのがあり、中心を軸に楕円を回転させてできる立体がそれ。回転楕円体の断面は楕円だったり、円だったりするのはそのため。 特殊でない楕円体はどこで切断しても楕円で円は現れないことになる。 次ぎに(2)だけど、紙の上に楕円を描く簡単な方法として、一定の長さの紐の両端を焦点となる2点にそれぞれ固定し、鉛筆の先端で紐がピンと張った状態を保って焦点を囲む周囲を一周しながら曲線を描くとそれが楕円となるのは良く知られている。 楕円が描いたら、2つの焦点を結ぶ直線を軸に楕円を回転させるとラグビーボール状の回転楕円体(長楕円体)になる。もしくは2つ焦点を結ぶ直線と直交し2つの焦点の中間を通る線を軸といして回転させても球を押しつぶしたような回転楕円体(扁平楕円体)ができる。 因みに地球は完全な球体ではなく、扁平楕円体に近い形状をしているらしい。そのため場所によって重力に差が出る。 さてここで問題になるのが、楕円の焦点は楕円の定義から2つあることが明らかだけど、回転楕円体や一般の楕円体の場合の焦点はどこにあるのかね? 長楕円体の場合は2つの焦点を結ぶ直線を軸対称にしているので焦点の位置は確定するけど、扁平楕円体は焦点が回転するので円状にあることになる? 回転楕円体ではなく一般的な楕円体の場合はどうなる? 楕円に関しては古くからその円周長を求める方法を模索されていたが、18世紀になって微積分の重要な問題となって各種積分法が考案された歴史がある。そのため検索すると楕円の面積とか楕円体の表面積に関する説明ばかりで、それ以前の楕円体とはなんぞや、その焦点とはなんぞやという説明がおろそかになっている。面積や体積を計算する上で必要なのは、楕円の長軸半径と短軸半径だけで争点の位置はそれで決まるので深入りしなくていいということもある。 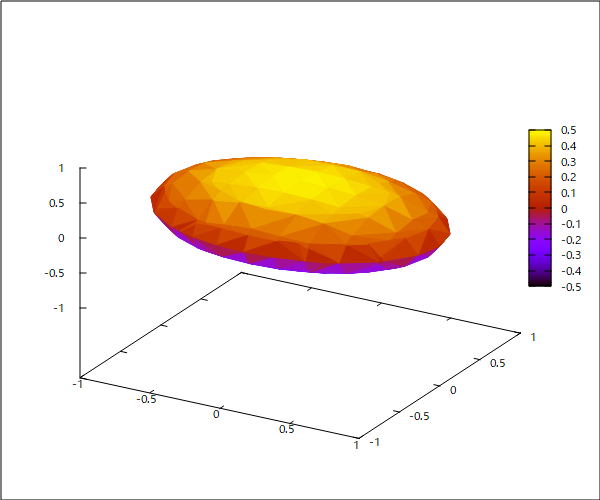 問題文をよくよく読むと、やっぱり焦点は直接関係ないと思われる。平面上の楕円ですら長径と短径で楕円の方程式は定まるので焦点の位置についてはそれと重複する情報となる。 解法のストラテジーとして思いつくのは、 (A) 帯電した楕円体導体が周囲の電荷のない空間に作る電界から等電位面の方程式を導く (B) 上はいきなり三次元なので難しいので、練習として断面が二次元楕円の楕円柱導体に帯電した電荷が周囲の電荷のない平面上に作る電界から等電位面の方程式を導く とりあえず、(B)の手始めとして楕円の方程式を導出してみるテスト。 楕円の定義として終点F1,F2がそれぞれ(-c,0), (c,0)とx座標軸状にあるとして、楕円上の任意の点P(x,y)とF1,F2を結ぶ線分の和が一定値(k)とする。 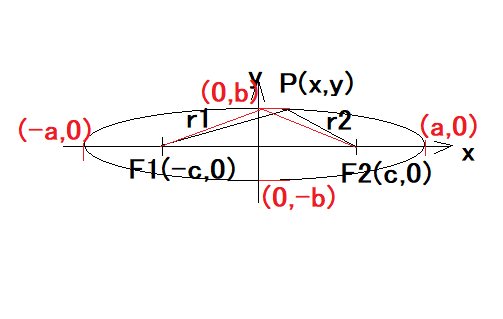 楕円の定義式から根号記号を消すために、式を二乗したり、根号のある単一項を辺の片方にだけに残して更に二乗すると二次の方程式が現れる。長軸と短軸の半径をa,b(a>b>0)とすると、kは長軸の半径の2倍となることから最終的に良くしられた楕円の方程式が導かれる。 楕円線電荷の作る電界を導出するには、楕円の微少線分の法線を知る必要がある。それにはまず楕円の方程式(陰関数表現)から楕円の接線の方程式を陰関数定理を用いて導出すると、 ということになる。 法線は接線と直交するので、以下の関係が成り立つ、 ということになる。 さて問題は法線の方程式は得られたものの、楕円の外の任意の点の電界を導出するには、楕円上の線分に均等に分布した電荷が成す電界を積分する必要がある。 どうすんだこれ(´Д`;) (続く) |
| webadm | 投稿日時: 2024-5-3 16:44 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
電荷のない空間での等電位面 λをパラメータとするφ(x,y,z,λ)=0 なる曲面群が、電荷のない空間にあって、等電位面になるための条件は
がλだけの関数になることであることを示せ。 というもの。 ふう、やっと電気力線問題が終わったぽいね(´∀` ) でも残るはラスボス級の問題ぽい(;´Д`) 問題の意味が解らない(´Д`;) 著者の解をチラ見すると、どうやらLaplace方程式の応用問題ぽい(´∀` ) で、問題の関数φはx,y,z,それにλをパラメータとして持つ陰関数であるので、λがx,y,z に依存するとすれば、x,y,zに関する二階の微分は以下の通り。 y,z に関しても同様に、 従って電荷のない空間ではLaplace方程式を満たすことから、以下の関係が成り立つ。 従って題意の関数Fの定義より、 故にλのみに依存する関数ということになる。 まあ、著者の解法をなぞっただけなんだけど(´Д`;) 別解としては、途中までは一緒だけど、先に題意の関数Fの分子のλに関するLaplace方程式を導出して代入してみるテスト これらを題意のFの式の分子のλに関するLaplace方程式に代入すると、 同様に関数Fはλにのみ依存すること導かれた。 それ以外の別解、例えばFがλ以外にも依存する場合にLaplace方程式が成立しない等の矛盾が発生することを示すなどのアプローチを考えるのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2024-4-27 16:45 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
続々:無限並行直線と電気力線 それぞれ、ρ、ρ、-ρ'(ρ'<2ρ) の線密度で帯電した無限長の平行導線があり、それらに直角な平面との交わりをそれぞれ、 A, B, C とすると ABC が正三角形をなすとき、A から出る電気力線のうち、 C 点に達するものと無限遠点に向かうものとの境界をなすものは AC とどのような角度で出るか?
というもの。 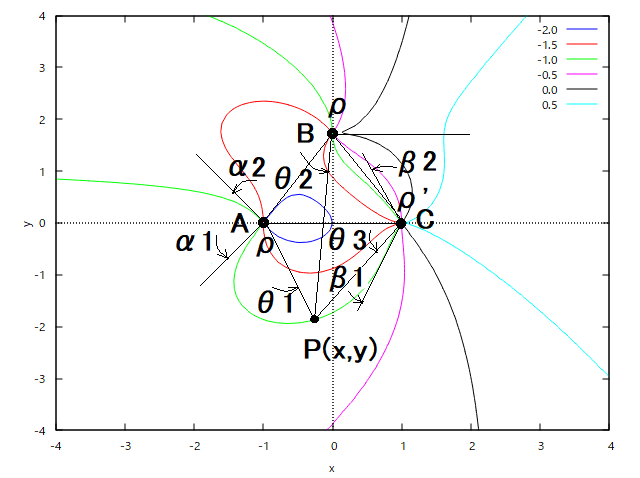 これは以前に直線上の点電荷と電気力線の問題で似たようなものがあったので、それの無限平行直線版である。 とりあえず電気力線をプロットしてみると著者の図とちょっと経路が違うものの、ループ状の電気力線がAから出てCへ向かっている様子が確認できた。 次ぎは電気力線の出口と尻尾のそれぞれについて電気力線の方程式をたてて、それらが同じ電気力線上であれば同値であることを利用してA点から出るときの角度α1,α2を求めることにする。 (2024.04.29) よくよく考えたら、以前の同種の問題では必ず電気力線が出るときと入る時の角度を定義していたが、この問題では出る時の角度を導出することだけを求めているのに対して、入る時の角度については何も情報を与えていないことに気付いた。 A から出る電気力線は無数にあり、また C に入る電気力線も無数にあるため、特定の電気力線を議論するには、A から出る角度だけでなく、 C に入る角度も特定する必要がある。 著者の解をチラ見すると、最初に問題文で欠落している C に入る時の角度を図と共に便宜的に仮定している。 これをやらずして問題を解くことは不可能なのであるから、出題者は予めそれも暗黙の内に題意に含めているとしか考えられない。 まあ、それに気付くか気付かないかで問題が解決できるか出来ないかの二択のどちらかになってしまう。 工学系とか物理系の問題解決には、大抵の場合そういった頓知が不可欠であり、人間の発想の豊かさが求められることは否めない。 物理学とかでは厳密に代数的に解が求められなくても、近似や実験による測定値の統計という手段をつかっておおよそこの値に収束するという結論で終わることも多い。代数的には解けていないが、物理現象を説明したり利用するにはそれで十分な事が多い。 なんの話だったっけ? ああ、A から出て C に入る電気力線を特定するには、A から出る角度だけではなく、C に入る角度も特定する必要があるということだった。 さて、問題を解く上での難しさはそれだけではなかった。 以前の直線上の点電荷の問題では、A から出て無限遠点に向かう電気力線はぎりぎり Cからそれて点電荷が並ぶ直線に沿って無限遠点に向かうため無限遠点に向かう角度が特定できたが、この問題では断面が正三角形状に配置された無限長線電荷であるため、C に向かわずに無限遠点に向かった電気力線の向きが特定できない。 なので当初無限遠点に向かう条件を使うつもりだったが、それは使えないということが判明した。 そのため著者の解にあるように、A から出て正三角形の外側を通って C に入るものと、A から出て 正三角形の内側を通って C に入る電気力線を考え、C に入る時にはどちらも C を通る正三角形の対称線に沿っているという条件を加える必要がある。 実際に上の条件は妥当なのかどうか謎である。 というのも、Maximaを使って正三角形状に並んだ無限並行直線の電気力線をプロットするために苦労したのは、電気力線の定義に反するようなものがプロットされてしまうためである。 この問題では2つの無限並行直線が同じρという線密度であるのに対して、残りひとつは、他の2つの線密度の総和よりも少ない逆極性の線密度ρ’という設定なのに対して、何故か同じ極性の2つの無限並行直線同士を結ぶ電気力線が現れてしまう点である。 また、著者の図と同じように、A と B を垂直線上に配置して、C をそれと直交する対称線上に正三角形を構成する位置に配置した場合、電気力線の形が正三角形の向きを変えただけで似ても似つかないものに変わってしまう謎現象があった。 著者の図では B から出る電気力線については何も描かれていないのでどうやって描いたかは謎だ。 なんの話だったっけ? ああ、電気力線を特定するための条件ね。 で残る疑問は、著者の解は本当にA から出て C に入る電気力線と A から出て 無限遠点に向かう電気力線の境界を本当に導出しているのかという点である。 今日ではどの電磁気学の教科書も電気力線に深入りしないのでこんだけ電気力線の問題を扱っているのはこの本だけなんだけどね。 たぶんに著者が根拠としているのは、A から出て C に入る同値の方程式を持つ電気力線は外回りと内回りの二つあり、それらがC 点では連続である(同値の微分係数が存在する)ということだと考えられる。 同じ電気力線であれば、最初の電気力線の問題で提示された電気力線の微分係数と電界の成分の比が比例関係にあるということを思い出せば、同じ電気力線なら C 点でも同じ接線(微分係数)を持つ要があるからである。 すなわち C 点に入る同じ電気力線の方程式の値を持つ外回りと内回りの電気力線が C 点に入る際に連続でないものは存在しないし、その場合には無限遠点に向かうものと考えられる。 ちょっと飛躍があるかもしれないが、そういうことだと仮定しよう。 著者の解では、C 点に入る電気力線の角度をいきなり導入しているけど、ここでは外回りと内回りをそれぞれβ1、β2としてα1、α2を解いた後、著者のβ1、β2の値を代入して同じ結果になるか検証することにする。 上のグラフではわかり難いので、位置関係は同じまま書き直すと、 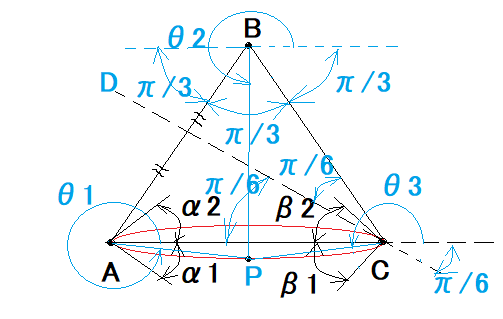 まず外回りの電気力線から、 外回りする電気力線は、A 点近傍のPで以下が成り立つ、 同じ電気力線が C 点に外回りで入る時に以下が成り立つ、 同じ電気力線であれば、方程式の値は同値なので、以下の関係が成り立つ、 従ってα1に関して解けば、 ということになる。 ここで、著者の解で仮定している、外回りで C に入る角度をβ1に代入すると、 ということになる。 一方で、内回りする電気力線は、A 点近傍のPで以下が成り立つ、 同じ電気力線が C 点に内回りで入る時に以下が成り立つ、 同じ電気力線であれば、方程式の値は同値なので、以下の関係が成り立つ、 従ってα2に関して解けば、 ということになる。 ここで、著者の解で仮定している、内回りで C に入る角度をβ2に代入すると、 ということになる。 著者の解ではθ1,θ2,θ3の基準がABを二等分するCDを通る対称線を基準にしているのに対して、ここではACに並行な線を基準にしている点が異なるが、同じ結果が得られた。 試しに、ρ=1, ρ'=1, ρ'<2ρという条件でα1、α2を計算してみると、どちらもπ/2となり、ACに対して垂線方向に電気力線が出て行くことがわかる。 P.S この問題はθ1,θ2,θ3の基準線については共通であれば任意だが、α1、α2それにβ1,β2はそれとは異なり、ACを基準にした角度である点に注意が必要だった。 結局のところ著者の図のような電気力線が存在するのかどうか、電気力線の方程式を使ってMaximaでプロットしても似ても似つかぬ電気力線しかプロットされない原因は不明。その原因を見つけるのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2024-4-27 5:06 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
続:無限並行直線と電気力線 それぞれ、λ、-λ/2, -λ/2 の線密度で帯電した無限長の平行導線があり、それらに直角な平面との交わりを A, B, C とすると、AB=AC であるとき、A から対称線付近にそって外方に出て B 点に入る電気力線が BC となす角は ∠BAC に等しいことを示せ。
というもの。 これを読むと、複数の無限平行直線は前の直線上の点電荷のように一直線上に並んでいるとは限らないのな。 ならどうやって電気力線をプロットすればすればいいかね。前の問題では電気力線の方程式には線電荷の座標ではなく、電気力線上の点Pと各線電荷を結ぶ直線と一定方向との成す角θiしか出てこない。 となると、点Pと線電荷を結ぶ線分と一定方向との成す角が判っても、線電荷の位置は点Pと線電荷を結ぶ線分の延長線上のどこでもいいことになってしまうんだが(´Д`;) どうすんだこれ(;´Д`) 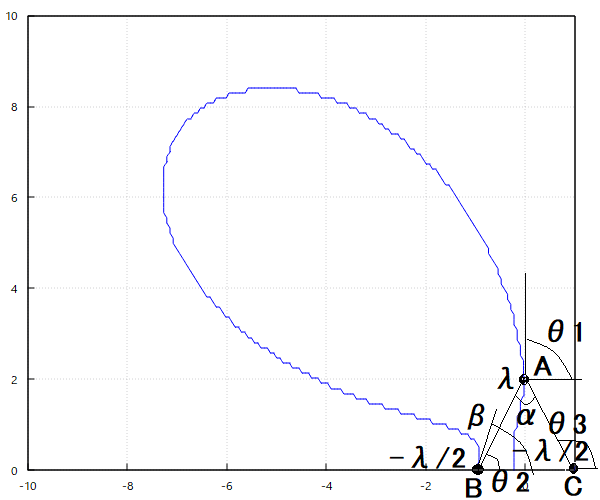 なんとか苦労してプロットしてみたが、著者の図とは似てもにつかないな。 とりあえず、ABCを結ぶ三角形の対称線に沿ってAから出て,外回りでBに入る電気力線のひとつを描いてみた。 後は前問の電気力線の方程式で、A点を出る点と、B点に入る 点が同じ電気力線上であれば方程式の値は同値である条件を利用してB点に入る時の角度を導出すればいいことになる。 A 点を出るときθ1=π/2, θ2=(π-α)/2, θ3=π-(π-α)/2 なので電気力線の方程式から以下の関係が成り立つ。 おろ、ゼロになるのか。 また、B 点に入るとき、θ1=π+(π-α)/2, θ2=β, θ3=π なので電気力線の方程式から以下の関係が成り立つ。 従って、同じ電気力線上の2点は電気力線の方程式は同値となるので、 ということになる。 プロットと違うように見えるけど,BCから時計回りでαの角度戻した方向から B に入るということになる。 θ1=-(α+(π-α)/2)と時計回りに負の値とすると、β=-(2π+α)となり、時計回りに一周+αということでBCに対してαの角度でBに入るので同値である。 最初θ1=α+(π-α)/2とおいて計算すると、β=αとなって喜んだんだが、良く考えたら角度の測り方がθ2,θ3と違っているのに気づいてやり直したら、BCに対して時計回りでαの方向ということになった。その場合も、一度ABCの内側に回り込んで入るということになる。 |
| webadm | 投稿日時: 2024-4-19 20:50 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
無限並行直線と電気力線 ふう、天気が良いね(´∀` )
洗濯日和! それはよいとして、ようやく直線上の点電荷と電気力線に関する問題が尽きたらしいけど、今度は無限並行直線と電気力線の問題軍来たこれ(;´Д`) 最初の問題は、直線上の点電荷の問題の時と同様に、電気力線の陰関数表記の方程式に関する問題。 単位長さあたり、λ1,λ2,...,λn に帯電した n 本の無限並行直線があるとき、電気力線の方程式は、各線とその上の点とを結ぶ直線が一定方向となす角をθ1,θ2,...,θn とするとき、次式で与えられることを示せ。 というもの。 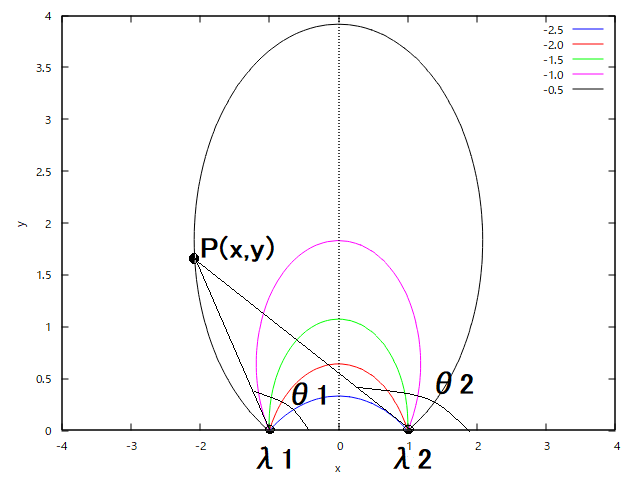 以前の直線上の点電荷の時は、各点電荷と電気力線上の点を結ぶ直線と点電荷が並ぶ直線との成す角で表したが、今度は単位長さ当たりの電荷量と各無限直線と電気力線上の点を結ぶ直線が一定方向と成す角で表す点が異なる。 一定方向は特に限定されていないので、共通の方向であれば、どの方向であっても良いということだろう。 あるいは、直線上の点電荷を一様に帯電した無限帳直線の断面に置き換えて考えても良いかもしれない。 以前の直線上の点電荷のケースではガウスの法則で電荷の総量が有限であるので電束を計算することができたが、今回は無限並行線に帯電した電荷の総量が無限になってしまうので、無限並行線全体を視野に入れるのは都合が悪い。 単位長さあたりの電荷量が与えられているので、有限区間ではガウスの法則が使えないこともない。無限平行線なのでz軸方向に線が延びているとすると、どのz座標のxy平面でみても電気力線は金太郎飴のように同じ姿になることになる。 前の直線上の点電荷の時には、点電荷だったのでガウスの法則と立体角を使って電気力線の方程式を導くことができたが、今回は点電荷ではなく無限超線電荷なので事情が異なる。 無限超線電荷の場合は電界は線電荷と直行する平面に平行な方向成分のみとなり、それ以外の方向成分は相殺されて存在しないことになる。 上記は証明しなくても自明なので、それによって線電荷を取り囲む幅1の円筒表面で電界もしくは電束を積分すればそれぞれλi/ε0,λiということになる。 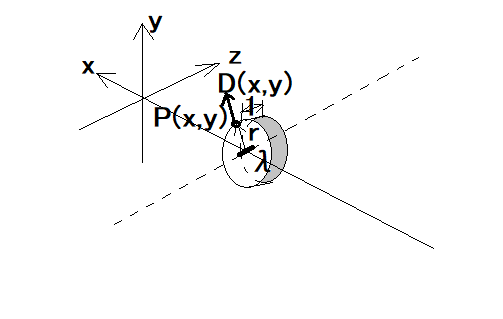 この事実を応用して、同じ電気力線上の任意の点P(x,y)を通る単位長さの円筒の断面を通る電束を線電荷と点Pを結ぶ線分とx軸のなす角θiで表せば、線電荷が直線上に複数並んでいる場合、それらの電束の総和は一定であるはずである。 次に、複数の無限超線電荷がx軸上に平行に並んでいる際に任意の電気力線(曲面)を通る電束もしくは電界を求める必要がある。 曲面や曲線だと都合が悪いので、直線上の点電荷の時に用いたように電気力線の任意の点を通るx軸に垂直な直方体の平面で電束や電界を積分してもそれぞれλ、λ/ε0となることを利用する。 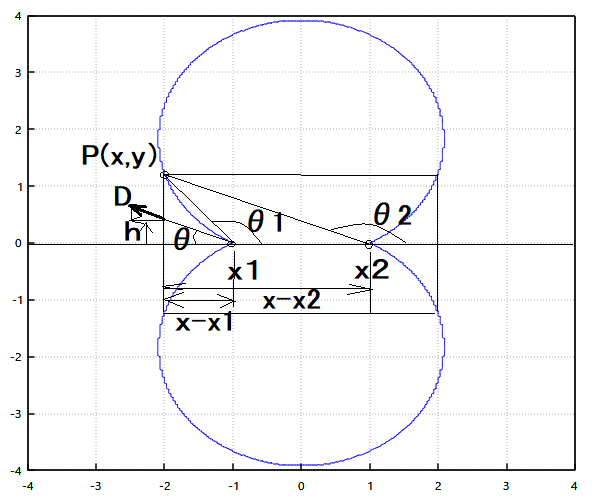 ということになる。 従って複数の並列に並んだ無限超線電荷の成す任意の電気力線上の点では以下の関係が成り立つことになる。 ということになる。 著者の解とは異なるアプローチでもできたじゃないか( ´∀`) Maximaで電束密度を積分した結果がatanになるのを見るまでは正直道間違えているかもと半信半疑だったことは内緒だ( ´∀`) P.S 次の著者の問題を読んだら、この問題からそうだけど、無限線電荷は互いに平行であるという条件だけで、前の直線上の点電荷のように一直線上に並んでるとは書いてない罠(´Д`;) まあ、それでも同じ結果なんだけどね。 角無限線電荷のy座標をy1,y2,...,ynとした場合でも成り立つことを確かめるのは読者の課題としよう( ´∀`) |
| webadm | 投稿日時: 2024-4-17 11:42 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
ずっと続く?:直線上の点電荷と電気力線 一直線上の AB=BC なる3点、A, B, C にそれぞれ 3q, -q, -q の電荷がおかれているとき、
(1) A 点で AB となす角が、 であるような電気力線は B, C に到達しないこと、および (2) の電気力線は無限遠で AC と直角をなすことを示せ。 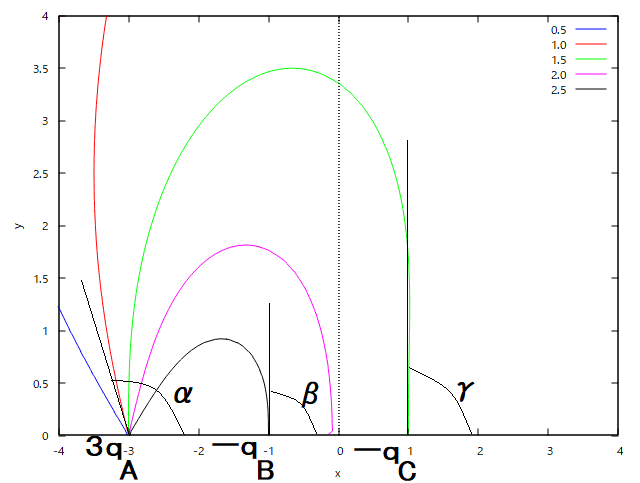 というもの。 これまでの問題の題意は電気力線が出る角度を求めるものだったのが、この問題では出る角度の条件が与えられた場合に、電気力線が点電荷に最終的に入るか否かを判別することが題意となっている。 前問と同様に、 を用いることにしよう。 A 点からαで出た電気力線が B 点にβの角度で入る場合、 ここで(1)の条件、 より、 一方で、与えられた電気力線が B 点に入るためには、βが実数値である必要から、αは以下の条件を満たす必要がある、 題意で与えられたα角では上の条件を満たさないため、与えられた電気力線は B 点に入ることはない。 同様に A 点からα角で出た電気力線が C 点にγ角で入る場合。 ここで先のα角、 で出た電気力線が C 点に入るには、γが実数値になる以下の条件を満たす必要がある 題意で与えられたα角は上の条件を満たさないので、γが虚数になってしまうため、与えられた電気力線は C 点に入らない。 (2)の設問に関して、無限遠点での電気力線の角度をθとした場合、以下の関係が成り立つ、 ここで(2)のαの条件、 すなわち、 これを先のθの式に代入すると、 ということになる。 |
| webadm | 投稿日時: 2024-4-17 10:28 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
更に続く:直線上の点電荷と電気力線 一直線上の AB=BC なる3点、 A, B, C にそれぞれ、q, -4q, q の電荷をおく場合、C を出る電気力線はすべて B に入るときに BC と 60°を越さない角をなすことを示せ。
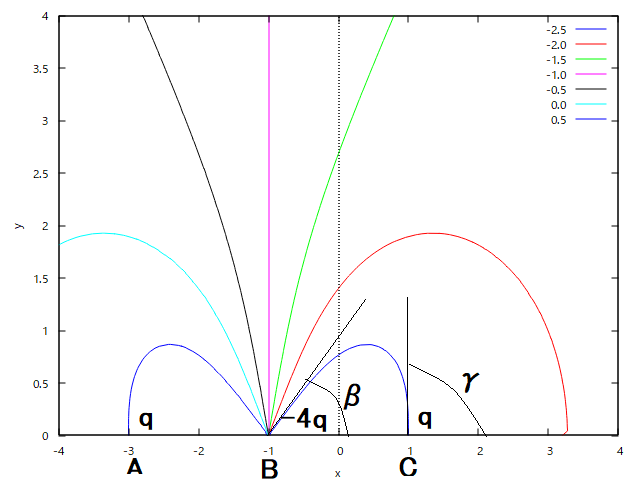 というもの。 前問と同様に、 が電気力線上の B点近傍と C点近傍で同値であることから、 が成り立つことになる。 ここで、 なので、 ということになる。 |
| webadm | 投稿日時: 2024-4-13 22:33 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
もっと続く:直線上の点電荷と電気力線 一直線上の AB=BC なる3点、A, B, C にそれぞれ、-q', q, -q'(q>2q') の電荷があるとき、B から出て A に入る電気力線が B において AB となす角は、
を越さないことを示せ。 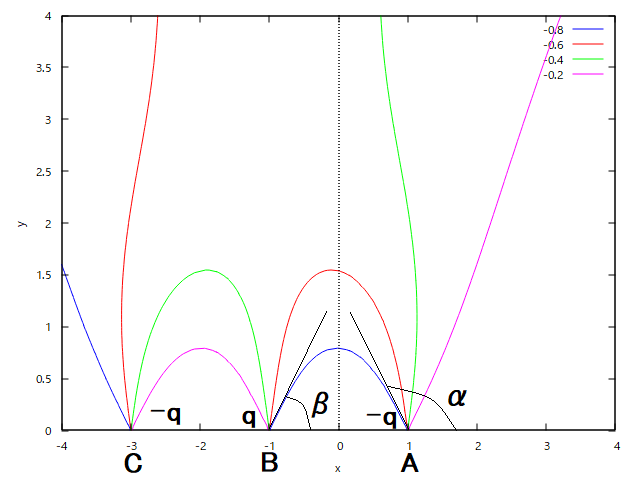 というもの。 題意の式に2 asin が出てきたあたりでヒントがありそう、 sin^2(θi/2) を使用した電気力線の陰関数定義が使えそうだ。 B点とA点に関して、同一電気力線上で以下の関係が成り立つ、 ここで、 であることから、 ということになる。 q>2q'の条件を満たさないと、-q'(C)から出発して-q'(A)に入るような電気力線とBから出た電気力線がそれと交わるように定義に反するようなものがプロットされる。 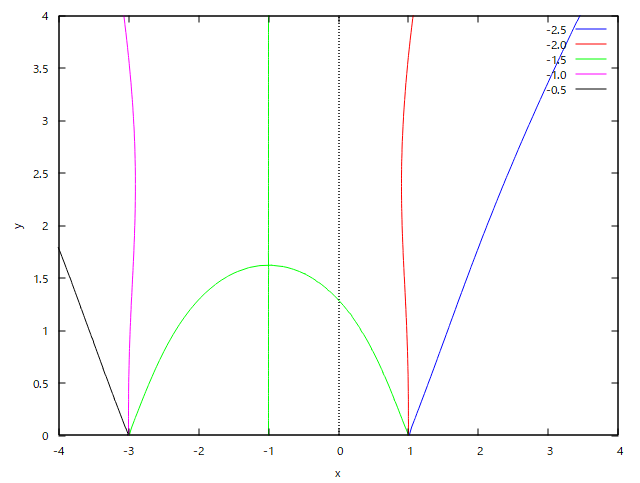 この原因を突き止めるのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2024-4-13 17:17 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
また続く:直線上の点電荷と電気力線 4q と -q の二つの電荷が2点 A, B におかれたとき、電気力線が AB に並行になる点 P の軌跡は
で与えられることを示せ。 というもの。 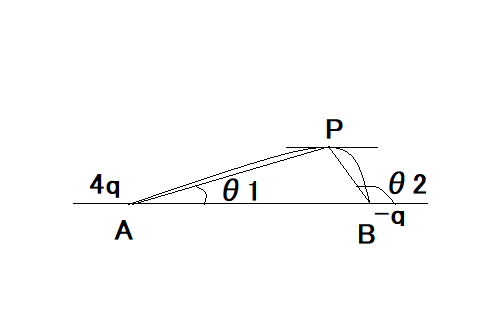 これは前問と設定は同じだけど、題意は電気力線の接線がx軸と平行になる(電界のy成分が0になる)点 P と2つの点電荷との間の距離の関係を導出する点が異なる。 電気力線の微分係数と電界の成分の関係式、 を用いることにしよう。 P(x,y)における電界のy成分は、 従って以下の関係が成り立つ、 これをAPについて解くと、3次方程式になるので虚数解を含めて解は3つあり、そのうち実数解は、 のみである。 |
| webadm | 投稿日時: 2024-4-13 3:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
まだ続く:直線上の点電荷と電気力線 4q と -g の二つの電荷が2点 A, B におかれたとき、B 点で AB に対して直角に入る電気力線は A 点をどのような角度で出るか?
というもの。 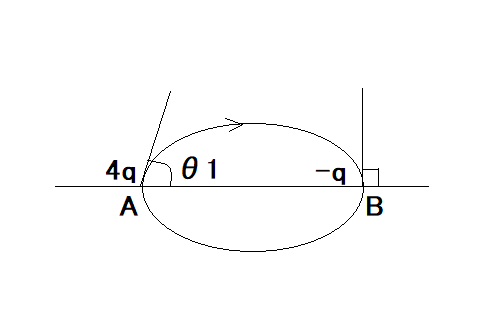 前問は電気力線が出る時の角度を求める問題だったが、今度は電気力線の入る時の角度を与えて電気力線が出る時の角度を求める問題。 これも前問と同じ要領で解いてみよう。 q1=4q, q2=-qといて、A点とB点において同じ電気力線では上の陰関数値が同値になるので、 ということになる。 著者の解答と違っているように見えるけど、数値計算すると同値であることがわかる。もはやラマヌジャンの世界だな(´∀` ) 本当に代数的に同値であるか確かめるのは読者の課題としよう(´∀` ) |
| (1) 2 3 4 » | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

