| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-7-18 22:32 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
Fourier変換と波形解析 いよいよ上巻の最後の章である。
通常では多相交流回路と歪み波に関しては数学的に難しいので電気回路理論の最後に教えるところが多い。本書では上巻と下巻とに分冊とする際に、下巻が厚くなるので本来は下巻の最後に登場すべき多相交流回路と歪み波の理論が上巻の最後に移されたのではないかと察する。 多相交流回路では対称座標法という面倒なテーマがあり、歪み波理論ではFourier変換というテーマが登場する。いずれも数理的で教えるのも面倒だし教わる方も理解に時間がかかる。 そもそも交流回路理論は、複素数を使う時点で数理的には複素関数解析と重なる。インピーダンス軌跡やアドミッタンス軌跡はそれぞれ複素数球面への写像として捉えると直感的に明快である。 歪み波に限らずあらゆる繰り返し波形を伴う信号は三角関数級数で近似できることを最初に発見したのが、名前の由来であるFourierである。 元来Fourierは生まれは貧乏で数学を独学し当時旬でもありライフワークでもあった熱方程式の解法の研究の過程で、一定区間定数を保つような三角関数級数を発見したことから、それを熱方程式の解法に応用した論文を発表した。 その主旨は「大概の関数は三角関数級数で近似できる」というはなはだ厳密さに欠き、素人学者の大胆な予想にすぎず最初は受け入れられなかった。 第一「大概の関数」とはなんだ? 例外があるのか? 第二に「近似できる」ということは完全に一致するわけではないのか? はなはだ数学的にはつっこみどころ満載であるが、確かに言われていることはその通りで大御所が身を乗り出して検証をしたがるほどニュース性を帯びていた。 当時のフランスの学会では過去二十数年に渡ってさしたる話題もなく、これといった論文募集のネタに事欠いていたため、当時の数学界の大御所であるラグランジェやラプラスらは、つっこみどころ満載のFourierのアイデアに目をつけ、次期論文募集テーマとして採用し広く論文募集を行った。 Fourierはめげずに論文を書き直し、応募したところ、ほどなく大賞を受賞することになった。 当時はまだ誰もFourier級数が収束する条件とかいうことを証明できる人は居なかった。これは後にディリクレや後生の数学者によってFourier解析という数学分野にまで大成するのを待たねばならなかった。 いずれにせよ最初に関数を三角関数級数で表すアイデアはFourierのオリジナルの発想であり、その数学界や物理学、工学への貢献は計り知れない。 数学界の大御所さえもFourierが登場するまで思いつかなかった発想をするのだから、Fourier自身は相当の変人であったことは史実からも知ることができる。 なんでもエジプトにナポレオンと一緒に遠征にいった後、フランスに戻ってもエジプトの気候が気に入って、自ら真綿で全身をくるみその上から包帯でぐるぐる巻きにしてまるでミイラのような姿で蒸し暑い部屋で研究に没頭するのが好きだったらしい。 その反面、乱世のフランスの時代に柳のように情勢の変化に適応して市長を務めながらライフワークの研究を続けたしたたかな人物であったようである。 なんの話だったっけ? ああFourier変換と波形解析ね。 今日教えられているFourier解析については後生の学者が敬意を表してFourierの名前をつけた定理も含まれており、どれがオリジナルかは判別できなくなっている。応用するにはどれがオリジナルかは意味がなく大成された理論を理解するのが重要であるためだ。 しかし反面、それが当時いかにオリジナルのアイデアが画期的であったかという点を忘れさせることにつながっている。まるで当たり前の話に見えてしまうのだ。決してそうではない。同じように熱方程式を研究していた大御所の学者が他にもいっぱいいたが、育ちが貧乏で職業学者でもないFourierが独自に見つけた発見であることが忘れられてしまっている。 Fourier級数は三角関数級数であるため、周期性のある関数だけを表すことができる。しかし時間を表す変数tを周期を表すTに変換しTを∞にすると繰り返し性の無い単発現象の関数も表すことができる。 オリジナルFourier級数は実数関数だが、複素関数に拡張すると更にその性質を良く理解し応用することができる。 もちろん実時間関数としてのフーリエ変換も有用で、JPEGやMPEGなどデジタル信号処理で使われている離散コサイン変換や離散フーリエ変換もフーリエ変換の一種である。 唯一の注意点としてはフーリエ級数もフーリエ変換も積分可能な関数にのみ適用可能で有る点である。また不連続点ではギブス現象と呼ばれるオーバーシュートやアンダーシュートが生じる。一部の参考書では級数項を∞にすれば完全に一致するようなニュアンスで説明されているものがあるが、それは限られた条件下であって、不連続点を含む場合は含まれない点に注意。 |
| webadm | 投稿日時: 2009-7-18 23:42 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
ひずみ波のFourier級数展開 これまでの交流回路理論では交流は単一周波数の正弦波であることを前提としてきた。
実際には物理的機械的な要因によって発電機の起電力は理想的な正弦波ではなく、変圧器も磁性体の非線形性(ヒステリンシス効果)から正弦波を入れても出力は歪んでしまう。 従って実務ではひずんだ交流信号を扱う必要が出てくる。 一方でオーディオ信号の増幅回路ではひずみは大敵なのでいかに歪まないようにするか苦心する。オーディオアンプの性能のひとつとしてひずみ率があり、それは入力信号に無ひずみの正弦波信号を入力し出力信号に含まれる高調波ひずみレベルの比率を測定することによって行われるのは承知の通り。 周期T=2π/ωを持つひずみ波は以下のようにFourier級数で表すことができる。 y(t)=Σan*sin(nωt)+b0+Σbn*cos(nωt) (n=1,∞) ここでan,b0,bnはFourier係数とよばれ以下で与えられる。 an=(2/T)∫y(t)*sin(nωt)dt (t=0,∞) b0=(1/T)∫y(t)dt (t=0,∞) bn=(2/T)∫y(t)*cos(nωt)dt (t=0,∞) また An=sqrt(an^2+bn^2) θn=tan^-1(bn/an) を用いると以下の様に正弦はのみの級数として表される。 y(t)=b0+ΣAn*sin(nωt+θn) (n=1,∞) b0をひずみ波の直流分、A1*sin(ωt+θ1)を基本波、An*sin(nωt+θn)を第n高調波と呼ぶ。これらの正弦波の集合を周波数スペクトルと呼ぶ。 という感じで天下り的に示されてもなんのことかさっぱり理解できないと思う。 これらは集大成されたFourier級数の総まとめ的な内容であり、それを導出する過程は説明されていない。 なのでひとつひとつオリジナルのアイデアから考え直してみよう。 WikipediaによればFourierが最初に発見した三角関数級数は以下のようなものだった y(t)=Σ((-k)^k/(2*k+1))*cos((2*k+1)*x) (k=0,∞) これを実際にk=0,3までの項でプロットしてみよう。 wxplot2d([-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$ 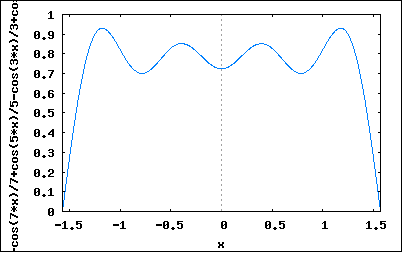 むむ、何やら台形の形をしている。 更に項数を増やしてk=0,7でプロットしてみよう。 wxplot2d([-cos(15*x)/15+cos(13*x)/13-cos(11*x)/11+cos(9*x)/9-cos(7*x)/7+cos(5*x)/5 -cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$  大分台形らしくなってきた。最高値は平坦になるまで収束するのだろうか? 更にk=0,11でプロットしてみよう。 wxplot2d([-cos(23*x)/23+cos(21*x)/21-cos(19*x)/19+cos(17*x)/17-cos(15*x)/15+cos(13*x)/13 -cos(11*x)/11+cos(9*x)/9-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$ 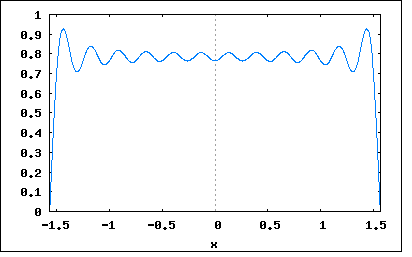 どうやら段々と平坦になってきているのは確か。 これを範囲を広げてプロットしてみると 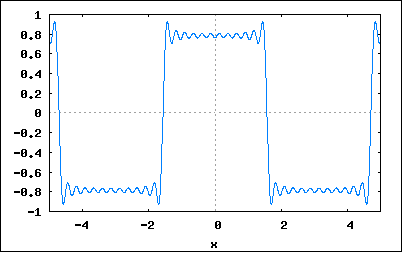 典型的な矩形波の繰り返し波形が見えてくる。 おそらくFourierはわくわくしながら色々な関数を試してみたに違いない、その中でほどよく収束する区間と収束しない区間があるのを認めざるを得ず、それがどうした条件でそうなるのかは独力で明らかにすることはできなかったと思われる。それが後生に研究課題を多く提供した点は誠実な学者としての誠意である。 後にFourier級数を機械的にプロットする装置を作った人が居て、やはり最初に矩形波をプロットさせたところ不連続点でプロッタが激しく振動を繰り返すという怪現象に見舞われた。それは後にギブスが数学的に証明したギブス現象と呼ばれるもので、関数の不連続点では収束せずにアンダーシュートとオーバーシュートが生じるというものである。 先のプロット画像でも急激に値が変化する点ではオーバーシュートとアンダーシュートが顕著であることからも確認できる。 そんな訳ありではあるが、近似というレベルでは十分実用になる範囲のものである。工学的には細かい誤差を追求するよりもいかに手軽に近似解が得られるかが重要である。 そこで話を本論に戻そう。 天下り式にFourier係数の定義が示されているが、a0が無いのは何故だろう? 考えてみればわかるが本来は y(t)=Σan*sin(nωt)+Σbn*cos(nωt) (n=0,∞) と表すのがシンプルだが n=0の場合 y(t)=a0*sin(0)+b0*cos(0) (n=0) ということになる。sin(0)=0、cos(0)=1なので y(t)=b0 ということになりa0の項は消える。 いろいろな本ではsinとcosの順番が入れ替わっていたりするものがあったり、数学系の本では直流分に1/2という係数がついているものがある。 それ以前に著者のFourier係数の式がどうやって導出されたのか気になる。 ここで以前に入手した回路網解析の古書を参考にして検証してみよう。 Fourier係数の式を導出するには前出のFourier級数の式を最長周期で積分する y(t)=Σan*sin(nωt)+Σbn*cos(nωt) (n=0,∞) 最長周期はt=0〜Tとすると ∫y(t)dt=Σan*∫sin(nωt)dt+Σbn*∫cos(nωt)dt (n=0,∞ ωt=0,T) ここでn=0に限定すると ∫y(t)dt=∫b0*dt (t=0,T) =b0*T 従って b0=(1/T)∫y(t)dt (ωt=0,T) ということになる。 次ぎにn=0以外でのanとbnを導く必要がある。 n=奇数に限定すると ∫y(t)dt=an*∫sin(nωt)dt (n=奇数 t=0,T) 両辺にsin(nωt)を乗じると ∫y(t)*sin(nωt)dt =an*∫sin(nωt)^2dt an*∫sin(nωt)^2dt=an*∫(1-cos(nωt)^2)dt =an*∫(1-(1+cos(2nωt))/2)dt =an*∫(1/2-cos(2nωt)/2)dt =an*T/2 従って an=(2/T)*∫y(t)*sin(nωt)dt ということになる。 同様にbnも n=偶数に限定すると ∫y(t)dt=bn*∫cos(nωt)dt (n=偶数 ωt=0,T) 両辺にcos(nωt)を乗じると ∫y(t)*cos(nωt)dt =bn*∫cos(nωt)^2dt =bn*∫cos(nωt)^2dt =bn*∫(1-sin(nωt)^2)dt =bn*∫(1-(1-cos(2nωt))/2)dt =bn*∫(1/2+cos(2nωt)/2)dt =bn*T/2 従って bn=(2/T)*∫y(ωt)*cos(nωt)dt ということになる。 youtubeとかで見ることが出来るMITの数学の講義の中にFourier級数というのがあり、見てみたら、信号が任意の正弦波の合成というところから出発している。 ちょうど著者の説明と逆順にたどることになる。 y(t)=ΣAn*sin(nωt+θn) (n=0,∞) n=0の時 y(t)=A0*sin(θ0) これをb0と置くと b0=A0*sin(θ0) ということになる。 また三角関数の合成定理から sin(nωt+θn)=sin(nωt)*cos(θn)+cos(nωt)*sin(θn) 従って y(t)=b0+ΣAn*(sin(nωt)*cos(θn)+cos(nωt)*sin(θn)) (n=1,∞) =b0+ΣAn*sin(nωt)*cos(θn)+ΣCn*cos(nωt)*sin(θn) ここで an=An*cos(θn) bn=An*sin(θn) と置くと y(t)=Σan*sin(nωt)+b0+Σbn*cos(nωt) ということになり最初の式が導かれることになる。 また sqrt(an^2+bn^2) =sqrt(An^2*cos(θn)^2+An^2*sin(θn)^2) =An tan(θn) =sin(θn)/cos(θn) =(bn/An)/(an/An) =bn/an 従って θn =tan^-1(bn/an) ということになる。 まずはこの程度の理解に止めておこう。 |
| webadm | 投稿日時: 2009-7-19 19:27 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
特殊な形のひずみ波 大概の繰り返し波形はフーリエ級数で近似できるということは理解できたが、実際に特定の繰り返し波形をフーリエ級数に展開しようとするとフーリエ係数を決定するのがやっかいである。
いくつかに特殊なケースがあり、必要なフーリエ係数も限定されることが知られている。 (1)対称波の場合 対称波とは最短繰り返し周期(T)の半周期毎に信号が極性反転して繰り返すもの。 y(t+T/2)=-y(t) が成立する場合にはフーリエ級数は以下の様に限定される。 a2m+1=(4/T)∫y(t)*sin((2m+1)*ωt)dt (m=0,1,2,... t=0,T/2) b2m+1=(4/T)∫y(t)*cos((2m+1)*ωt)dt (m=0,1,2,... t=0,T/2) a2m=b2m=b0=0 すなわち奇数次(1,3,5,...)の高調波のみの三角関数級数は対称波になるという。 (2)奇関数の場合 時間0を境にそれ以前の半周期とそれ以降の半周期とで象限を180度反転したような関数は奇関数と呼ばれる。 y(t)=-y(-t) この場合フーリエ係数は an=(4/T)∫y(t)*sin(nωt)dt (t=0,T/2) b0=bn=0 すなわちsin級数のみのフーリエ級数は奇関数ということになる。 b0=0なので (3)偶関数の場合 最短繰り返し周期(T)の半周期を境にして鏡に映したように前半と後半の周期の波形が対称な関数を偶関数と呼ぶ。 y(t)=y(-t) an=0 b0=(2/T)∫y(t)dt (t=0,T/2) bn=(4/T)∫y(t)*cos(nωt)dt (t=0,T/2) すなわちcos級数のみのフーリエ級数は偶関数であると言える。 偶関数の場合のみb0≠0のケースがあることになる。 しかし良く考えると、周期の基点をどこにするかによっては対称波や奇関数、偶関数になったりする気がする。 実際にプロットしてみようと思うと、計算が結構面倒なことがわかる。三角関数と関数の積を積分しないといけない。この操作は特定の高調波との相関係数を求めることを意味する。 実際にそれぞれの簡単な波形グラフを元にフーリエ級数を計算してみよう。 上の様な矩形波を考えてみよう。見ると明らかに偶関数であると同時に対称波でもある。 y(t)の値は -V (ωt=-π〜-π/2) V (ωt=-π/2〜π/2) -V (ωt=π/2〜π) という値を取る。 従ってフーリエ係数は b0=(2/T)∫y(t)dt (t=0,T/2) =(2/T)*(∫Vdt+ (t=0,T/4) ∫-Vdt) (t=T/4,T/2) =(2/T)*(T/4-T/4) =0 bn=(4/T)∫y(t)*cos(nωt)dt (t=0,T/2) =(4/T)*(∫V*cos(nωt)dt+ (t=0,T/4) ∫-V*cos(nωt)dt) (t=T/4,T/2) =(4*V/T)*([sin(nωt)]- (t=0,T/4) [sin(nωt)]) (t=T/4,T/2) =(4*V/T)*(sin(nωT/4)/nω-(sin(nωT/2)-sin(nωT/4))/nω) =(4*V/nωT)*(2*sin(nωT/4)-sin(nωT/2)) (n≠0) ここで T=2π/ω を代入すると bn=(2*V/nπ)*(2*sin(nπ/2)-sin(nπ)) (n≠0) =(4*V/nπ)*sin(nπ/2) すなわち bn=(4*V/(nπ)) (n=1,5,9,...) bn=(-4*V/(nπ)) (n=3,7,11,...) bn=0 (n=2,4,6,...) ということになる。三角関数の各定積分はMaximaを使って求めた。 従って y(t)=(4*V/π)*(cos(ωt)-(1/3)*cos(3*ωt)+(1/5)*cos(5*ωt)-(1/7)*cos(7*ωt)+...) ということになる。 これをプロットしてみると。 wxplot2d([(4*(-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)))/%pi], [x,-2*%pi,2*%pi])$ 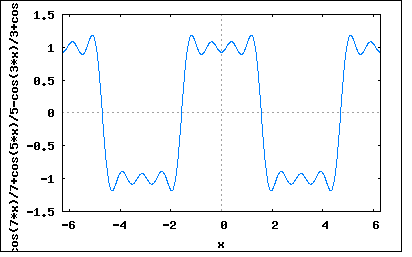 近似な波形が合成されるのが確認できた。三角関数の定積分を求めるのが面倒だ。 今度は同様に奇関数についてやってみよう。 上のような奇数関数な三角波をフーリエ級数に展開してみよう。 奇関数なのでt=0〜T/2の範囲でy(t)は (2*V/π)*ωt (t=0〜T/4) (2*V/π)*(π-ωt) (t=T/4〜T/2) をとる。 従ってフーリエ係数は an=(4/T)∫y(t)*sin(nωt)dt (t=0,T/2) =(4/T)*(∫(2*V/π)*ωt*sin(nωt)dt+ (t=0,T/4) ∫(2*V/π)*(π-ωt)*sin(nωt)dt) (t=T/4,T/2) =(4/T)*(2*V/π)*(∫ωt*sin(nωt)dt (t=0,T/4) +∫(π-ωt)*sin(nωt)dt (t=T/4,T/2) =(4/T)*(2*V/π)*(4*sin(nωT/4)-nωT*cos(nωT/4))/(4*n^2*ω) -(4*sin(nωT/2)-2*nωT*cos(nωT/2)+4*nπ*cos(nωT/2)-4*sin(nωT/4)+nωT*cos(nωT/4)-4*nπ*cos(nωT/4))/(4*n^2*ω))) =(4/T)*(2*V/π)*(-(2*sin(nωT/2)-nωT*cos(nωT/2)+2*nπ*cos(nωT/2)-4*sin(nωT/4)+nωT*cos(nωT/4)-2*nπ*cos(nωT/4))/(2*n^2*ω)) ここで T=2π/ω を代入すると an =(2*ω/π)*(2*V/π)*(4*sin(nπ/2)-2*sin(nπ))/(2*n^2*ω) =(4*V/π^2)*(2*sin(nπ/2)/n^2) (n≠0) ということになる。すなわち an=(8*V/π^2)*(1/n^2) (n=1,5,9,...) an=(8*V/π^2)*(-1/n^2) (n=3,7,11,...) an=0 (n=2,4,6,...) ということになる。 従ってフーリエ級数展開は y(t)=(8*V/π^2)*(sin(ωt)-(1/3^2)*sin(3*ωt)+(1/5^2)*sin(5*ωt)-...) ということになる。 プロットしてみると wxplot2d([(8*(sin(5*x)/25-sin(3*x)/9+sin(x)))/%pi^2], [x,-2*%pi,2*%pi])$  次数は少なくても十分三角波を近似していることがわかる。 相変わらず三角関数の定積分は面倒なのでMaximaで求めた。 今日はこのくらいにしておこう。 |
| webadm | 投稿日時: 2009-7-20 0:32 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
ひずみ波の実効値と電力 ひずみ波の実効値は正弦波交流の時と同様に瞬時値のRMS値として定義される。
ひずみ波の瞬時値電圧を e=E0+ΣEmn*sin(nωt+θn) (n=1,∞) とすると実効値は |E|=sqrt((1/T)*∫e^2dt) =sqrt(E0^2+|E1|^2+|E2|^2+...) で表される。 ただし |En|=Emn/√2 (n=1,2,3,...) なぜそうなるのか検証してみよう。 |E|=sqrt((1/T)*∫e^2dt)=sqrt((1/T)*∫(E0+ΣEmn*sin(nωt+θn))^2)dt =sqrt((1/T)*∫(E0^2+Em1^2*sin(ωt+θ1)^2+Em2^2*sin(2ωt+θ2)^2+... +E0*(Em1*sin(ωt+θ1)+Em2*sin(2ωt+θ2)+...) +Em1*sin(ωt+θ1)*(E0+Em2*sin(2ωt+θ2)+...) +...)dt =sqrt((1/T)*(∫E0^2dt+∫Em1^2*sin(ωt+θ1)^2dt+∫Em2^2*sin(2ωt+θ2)^2+... +∫E0*(Em1*sin(ωt+θ1)+Em2*sin(2ωt+θ2)+...) +∫Em1*sin(ωt+θ1)*(E0+Em2*sin(2ωt+θ2)+...) +...) ここで ∫E0^2dt=E0^2*T ∫Emn^2*sin(nωt+θn)^2dt =∫Emn^2*(1-cos(nωt+θn)^2)dt =∫Emn^2*(1-(1+cos(2*(nωt+θn))/2)dt =∫Emn^2*(1/2-cos(2*(nωt+θn)))dt =Emn^2*T/2 ∫E0*(Em1*sin(ωt+θ1)+Em2*sin(2ωt+θ2)+...)dt =0 ∫Em1*sin(ωt+θ1)*(E0+Em2*sin(2ωt+θ2)+...)dt =∫Em1*sin(ωt+θ1)*E0dt+∫Em1*sin(ωt+θ1)*Em2*sin(2ωt+θ2)dt+... =∫Em1*Em2*(cos(-ωt+θ1-θ2)-cos(3ωt+θ1+θ2))/2dt+... =0 従って |E|=sqrt((1/T)*(E0^2*T+ΣEmn^2*T/2) =sqrt(E0^2+ΣEmn^2/2) ここで |En|=Emn/√2 (n=1,2,3,...) と置くと |E|=sqrt(E0^2+|E1|^2+|E2|^2+...) ということになる。 同様に電力も瞬時値を最短周期で積分したものである。 負荷にかかる電圧と電流の瞬時値が e=E0+ΣEmn*sin(nωt+θn) i=I0+ΣImn*sin(nωt+θn+φn) とすると 消費される電力の瞬時値は p=e*i =(E0+ΣEmn*sin(nωt+θn))*(I0+ΣImn*sin(nωt+θn+φn)) =E0*I0 +E0*ΣImn*sin(nωt+θn+φn) +I0*ΣEmn*sin(nωt+θn) +ΣEmn*Imn*sin(nωt+θn+φn)*sin(nωt+θn) +ΣΣEmn*Imm*sin(nωt+θn)*sin(mωt+θm+φm) (n≠m) となり消費電力は最短周期の平均値なので Pa=(1/T)*∫pdt =(1/T)*∫(E0*I0 +E0*ΣImn*sin(nωt+θn+φn) +I0*ΣEmn*sin(nωt+θn) +ΣEmn*Imn*sin(nωt+θn+φn)*sin(nωt+θn) +ΣΣEmn*Imm*sin(nωt+θn)*sin(mωt+θm+φm))dt (n≠m) =(1/T)*(∫E0*I0dt +E0*∫ΣImn*sin(nωt+θn+φn)dt +I0*∫ΣEmn*sin(nωt+θn)dt +∫ΣEmn*Imn*sin(nωt+θn+φn)*sin(nωt+θn)dt +∫ΣΣEmn*imm*sin(nωt+θn)*sin(mωt+θm+φm)dt ここで ∫E0*I0dt=E0*I0*T E0*∫ΣImn*sin(nωt+θn+φn)dt=0 I0*∫ΣEmn*sin(nωt+θn)dt=0 ∫ΣEmn*Imn*sin(nωt+θn+φn)*sin(nωt+θn)dt =∫Em1*Im1*sin(ωt+θ1+φ1)*sin(ωt+θ1)dt+∫Em2*Im2*sin(2ωt+θ2+φ2)*sin(2ωt+θ2)dt+... =∫Em1*Im2*(cos(φ1)-cos(2ωt+2θ2+φ1))dt+∫Em2*Im2*(cos(φ2)-cos(4ωt+4θ2+φ2))dt+... =ΣEmn*Imn*cos(φn)*T ∫ΣΣEmn*Imm*sin(nωt+θn)*sin(mωt+θm+φm)dt =∫Em1*Im2*sin(ωt+θ1)*sin(2ωt+θ2+φ2)dt +∫Em1*Im3*sin(ωt+θ1)*sin(3ωt+θ3+φ3)dt +... +∫Em2*Im1*sin(2ωt+θ2)*sin(ωt+θ1+φ1)dt +∫Em2*Im3*sin(2ωt+θ2)*sin(3ωt+θ3+φ3)dt +... =∫Em1*Im2*(cos(-ωt+θ1-θ2-φ2)-cos(3ωt+θ1+θ2+φ2))dt +∫Em1*Im3*(cos(-2ωt+θ1-θ3-φ3)-cos(4ωt+θ1+θ3+φ3))dt +... +∫Em2*Im1*(cos(ωt+θ2-θ1-φ1)-cos(3ωt+θ2+θ1+φ1))dt +∫Em2*Im3*(cos(-ωt+θ2-θ3-φ3)-cos(5ωt+θ2+θ3+φ3))dt +... =0 従って Pa =(1/T)*(E0*I0*T+ΣEmn*Imn*cos(φn)*T) =E0*I0+ΣEmn*Imn*cos(φn) (n=1,∞) ここで |En|=Emn/√2 |In|=Imn/√2 と置くと Pa=E0*I0+Σ|En|*|In|*cos(φn) ということになる。 同様にひずみ波の皮相電力は電圧の実効値と電流の実効値の積で表される P0=|E|*|I| =sqrt((E0^2+Σ|En|^2)*(I0^2+Σ|In|^2)) また力率は消費電力と皮相電力の比なので cosφ=Pa/(|E|*|I|) ということになる。 |
| webadm | 投稿日時: 2009-7-22 10:39 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
ひずみ波の波形率、波高率、ひずみ率 ひずみ波の波形率、波高率、ひずみ率はそれぞれ以下の様に定義される。
波形率(form factor)=実効値/平均値 =sqrt((1/T)∫e^2dt)/ (t=0,T) (2/T)∫edt (t=0,T/2) 波高率(peak factor)=最大値/実効値 =EM/sqrt((1/T)∫e^2dt) (t=0,T) ひずみ率(distortion factor)=k=全高調波の実効値/基本波の実効値 =sqrt(|E2|^2+|E3|^2+|E4|^2+...)/|E1| 波形率や波高率は繰り返し波形のプロファイルとしてデジタルオシロとかで自動測定機能であったりする。波形率は分母が半周期の平均値とあるが、実際のところそうだとするとおかしなことになる。交流の時と同様に絶対値の平均値ならわかるが。 ひずみ率はオーディオ用のひずみ率計とかが表示する値である。入力信号(繰り返し波形)をノッチフィルターで基本波とそれ以外の高調波に分離して比率を求めるというものである。古いものはアナログだけど今はデジタルなのかな。 瞬時値をフーリエ級数に展開すると f(x)=Σan*sin(nωt)+b0+Σbn*cos(nωt) 従ってその実効値は sqrt((1/T)∫f(x)^2dt) =sqrt((1/T)∫(Σan*sin(nωt)+b0+Σbn*cos(nωt))*(Σan*sin(nωt)+b0+Σbn*cos(nωt))dt) =sqrt((1/T)∫(Σan^2*sin(nωt)^2 (n=1,∞) +Σbn^2*cos(nωt)^2 (n=1,∞) +b0^2 +Σan*bn*sin(nωt)*cos(nωt) (n=1,∞) +b0*Σan*sin(nωt)+b0*Σbn*cos(nωt) +ΣΣan*bm*sin(nωt)*cos(nωt))dt) (n≠m) =sqrt((1/T)∫(Σan^2*(1-(1+cos(2nωt))/2) +Σbn^2*(1-(1-cos(2nωt))/2) +b0^2 +Σan*bn*(sin(2nωt)+sin(0)) +a1*b2*sin(ωt)*cos(2ωt)+a2*b1*sin(2ωt)*cos(ωt)+...)dt) =sqrt((1/T)∫(Σan^2/2 +Σbn^2/2 +b0^2 +a1*b2*(sin(3ωt)+sin(-ωt)+a2*b1*(sin(3ωt)+sin(ωt))+...)dt) =sqrt((1/T)*(an^2*T/2+bn^2*T/2+b0^2*T)) =sqrt(b0^2+an^2/2+bn^2/2) ということになる。 従ってフーリエ係数がわかれば実効値はそれで表すことが出来る。 ここで高調波の実効値は |An|^2=an^2/2 |Bn|^2=bn^2/2 と置くと sqrt(Σ(|An|^2+|Bn|^2)) (n=2,3,4,...) ということになり 基本波の実効値も同様に sqrt(|A1|^2+|B1|^2) であるのでひずみ率は以下の様に表される ひずみ率=高調波の実効値/基本波の実効値=sqrt(Σ(|An|^2+|Bn|^2))/sqrt(|A1|^2+|B1|^2) ということになる。 P.S 著者は波形率の分母を瞬時値の半周期の平均値で対称波を前提としているが、他の参考書「電気回路」(朝倉書店)を見ると交流の場合と同様に瞬時値の絶対値の平均値である 波形率(form factor)=実効値/平均値 =sqrt((1/T)∫e^2dt)/(1/T)∫|e|dt (t=0,T) これだとすべての繰り返し波形に適用できる。こちらが正しいのではないだろうか? |
| webadm | 投稿日時: 2009-7-22 20:43 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
等価正弦波 ひずみ波は基本波と∞の高調波を含むため精密な計算には無理がある。
しかしひずみが十分少ない場合には高調波の影響を無視できるので、ひずみ波の実効値と基本波の周波数をもつ正弦波として近似することが有効である。 これを等価正弦波とよぶ。 この場合、力率の定義もひずみ波の場合と変わらないことになる。 力率=有効電力/皮相電力=Pa/(|E|*|I|) E,Iはひずみ波の電圧と電流の実効値 P.S 著者の等価正弦波の定義の記述は誤解を招く誤記がある。 「ひずみ波の実効値と基本周波数に等しい実効値および周波数をもつ正弦波に近似...」 二番目に出てくる実効値がなんなのか意味不明である。おそらく執筆時の誤記が訂正されないまま写植されてしまったのだろう。 本来なら 「ひずみ波の実効値と基本周波数に等しい と訂正されるべきだろう。 |
| webadm | 投稿日時: 2009-7-22 21:04 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
三相回路におけるひずみ波 三相交流発電機は空間的に対称な三個のコイルと磁石の相対的な回転運動により起電力を発生するため、起電力は正負対称な波形となり直流分や偶数次の高調波は含まれない。
これは先の「特殊な形のひずみ波」の対称波で学んだ通り対称波は奇数次の高調波しか含まれないという理由からである。 各相の電圧の高調波には以下のような性質がある、k=1,3,5,...として高調波の次数nが (1) n=3*kとなる高調波(第3,9,15,...)は、各相すべて零相分と等しい (2) n=3*k+4となる高調波(第7,13,19,...)は、基本波と同じ相回転の対称三相電圧となる。k=0のときは基本波そのものである。 (3) n=3*k+2となる高調波(第5,11,17,...)は、基本波と相回転が逆、すなわち逆相順の対称三相電圧である。 これを証明してみたいのだが、同じ内容を扱っている参考書が見あたらない。最近の参考書はそもそもひずみ波を扱っていなかったり、フーリエ級数までは扱っているが三相回路については扱っていなかったりする。 面倒なのだろうか、どうも対称座標法がからんでくるあたりからして計算が面倒くさそうだが、やってみることにしよう。 三相の各電圧の瞬時値をea,eb,ecとすると、それぞれは ea=a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+a7*sin(7ωt)+... eb=a^2*a1*sin(ωt)+a^6*a3*sin(3ωt)+a^10*a5*sin(5ωt)+a^14*a7*sin(7ωt)+... ec=a*a1*sin(ωt)+a^3*a3*sin(3ωt)+a^5*a5*sin(5ωt)+a^7*a7*sin(7ωt)+... 対称成分e0,e1,e2は ([e0],[e1],[e2]) =(1/3)*([1,1,1],[1,a,a^2],[1,a^2,a]).([ea],[eb],[ec]) =(1/3)*([1,1,1],[1,a,a^2],[1,a^2,a]).([a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+a7*sin(7ωt)+...],[a^2*a1*sin(ωt)+a^6*a3*sin(3ωt)+a^10*a5*sin(5ωt)+a^14*a7*sin(7ωt)+...],[a*a1*sin(ωt)+a^3*a3*sin(3ωt)+a^5*a5*sin(5ωt)+a^7*a7*sin(7ωt)+...]) =(1/3)*([a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+a7*sin(7ωt)+...+a*(a^2*a1*sin(ωt)+a^6*a3*sin(3ωt)+a^10*a5*sin(5ωt)+a^14*a7*sin(7ωt)+...)+a^2*(a*a1*sin(ωt)+a^3*a3*sin(3ωt)+a^5*a5*sin(5ωt)+a^7*a7*sin(7ωt)+...)],[a1*sin(ωt)+a3*sin(3ωt)+a5*sin(5ωt)+a7*sin(7ωt)+...+a^2*(a^2*a1*sin(ωt)+a^6*a3*sin(3ωt)+a^10*a5*sin(5ωt)+a^14*a7*sin(7ωt)+...)+a*(a*a1*sin(ωt)+a^3*a3*sin(3ωt)+a^5*a5*sin(5ωt)+a^7*a7*sin(7ωt)+...)]) =(1/3)*([(1+a+a^2)*a1*sin(ωt)+(1+a^3+a^6)*a3*sin(3ωt)+(1+a^5+a^10)*a5*sin(5ωt)+(1+a^7+a^14)*a7*sin(7ωt)+...],[(1+2*a^3)*a1*sin(ωt)+(1+a^5+a^7)*a3*sin(3ωt)+(1+a^7+a^11)*a5*sin(5ωt)+(1+a^9+a^15)*a7*sin(7ωt)+...],[(1+a^2+a^4)*a1*sin(ωt)+(1+a^4+a^8)*a3*sin(3ωt)+(1+a^6+a^7)*a5*sin(5ωt)+(1+a^8+a^16)*a7*sin(7ωt)+...]) =(1/3)*([(1+a+a^2)*a1*sin(ωt)+3*a3*sin(3ωt)+(1+a+a^2)*a5*sin(5ωt)+(1+a+a^2)*a7*sin(7ωt)+...],[3*a1*sin(ωt)+(1+a+a^2)*a3*sin(3ωt)+(1+a+a^2)*a5*sin(5ωt)+3*a7*sin(7ωt)+...],[(1+a+a^2)*a1*sin(ωt)+(1+a+a^2)*a3*sin(3ωt)+3*a5*sin(5ωt)+(1+a+a^2)*a7*sin(7ωt)+...]) =(1/3)*([3*a3*sin(3ωt)+...],[3*a1*sin(ωt)+3*a7*sin(7ωt)+...],[3*a5*sin(5ωt)+...]) =([a3*sin(3ωt)+...],[a1*sin(ωt)+a7*sin(7ωt)+...],[a5*sin(5ωt)+...]) e0=a3*sin(3ωt)+... e1=a1*sin(ωt)+a7*sin(7ωt)+... e2=a5*sin(5ωt)+... ということになり n=3*kの高調波は零相分に、n=3*k+4の高調波は正相分に、n=3*k+2の高調波は逆相分になることが証明された。 三相ひずみ電力は単相ひずみ波と同様に各相の電力の和であるので 対称三相ひずみ波の相電圧瞬時値は e=ΣEmn*sin(nωt) (n=1,3,5,7,...) 線電流瞬時値は i=ΣImn*sin(nωt+φn) (n=1,3,5,7,...) であるので電力の瞬時値は p=3*e*i =3*ΣEmn*Imnsin(nωt)*sin(nωt+φn) (n=1,3,5,7,...) =3*(ΣEmn*Imn*sin(nωt)*sin(nωt+φn) (n=1,3,5,7,...) +ΣΣEmn*Imm*sin(nωt)*sin(mωt+φm)) (n≠m) =3*(Em1*Im1*sin(ωt)*sin(ωt+φ1)+Em3*Im3*sin(3ωt)*sin(3ωt+φ3)+Em5*Im5*sin(5ωt)*sin(5ωt+φ5)+Em7*Im7*sin(7ωt)*sin(7ωt+φ7)+... +Em1*Im3*sin(ωt)*sin(3ωt+φ3)+Em1*Im5*sin(ωt)*sin(5ωt+φ5)+Em1*Im7*sin(ωt)*sin(7ωt+φ7)+... +Em3*Im1*sin(3ωt)*sin(ωt+φ1)+Em3*Im5*sin(3ωt)*sin(5ωt+φ5)+Em3*Im7*sin(3ωt)*sin(7ωt+φ7)+... +Em5*Im1*sin(5ωt)*sin(ωt+φ1)+Em5*Im3*sin(5ωt)*sin(3ωt+φ3)+Em5*Im7*sin(5ωt)*sin(7ωt+φ7)+... +Em7*Im1*sin(7ωt)*sin(ωt+φ1)+Em7*Im3*sin(7ωt)*sin(3ωt+φ3)+Em7*Im5*sin(7ωt)*sin(5ωt+φ5)+...) 従って有効電力は Pa=(1/T)∫pdt (t=0,T) =(1/T)∫3*(Em1*Im1*sin(ωt)*sin(ωt+φ1)+Em3*Im3*sin(3ωt)*sin(3ωt+φ3)+Em5*Im5*sin(5ωt)*sin(5ωt+φ5)+Em7*Im7*sin(7ωt)*sin(7ωt+φ7)+... +Em1*Im3*sin(ωt)*sin(3ωt+φ3)+Em1*Im5*sin(ωt)*sin(5ωt+φ5)+Em1*Im7*sin(ωt)*sin(7ωt+φ7)+... +Em3*Im1*sin(3ωt)*sin(ωt+φ1)+Em3*Im5*sin(3ωt)*sin(5ωt+φ5)+Em3*Im7*sin(3ωt)*sin(7ωt+φ7)+... +Em5*Im1*sin(5ωt)*sin(ωt+φ1)+Em5*Im3*sin(5ωt)*sin(3ωt+φ3)+Em5*Im7*sin(5ωt)*sin(7ωt+φ7)+... +Em7*Im1*sin(7ωt)*sin(ωt+φ1)+Em7*Im3*sin(7ωt)*sin(3ωt+φ3)+Em7*Im5*sin(7ωt)*sin(5ωt+φ5)+...)dt =(1/T)*3*(∫Em1*Im1*sin(ωt)*sin(ωt+φ1)+Em3*Im3*sin(3ωt)*sin(3ωt+φ3)+Em5*Im5*sin(5ωt)*sin(5ωt+φ5)+Em7*Im7*sin(7ωt)*sin(7ωt+φ7)+...)dt +∫(Em1*Im3*sin(ωt)*sin(3ωt+φ3)+Em1*Im5*sin(ωt)*sin(5ωt+φ5)+Em1*Im7*sin(ωt)*sin(7ωt+φ7)+... +Em3*Im1*sin(3ωt)*sin(ωt+φ1)+Em3*Im5*sin(3ωt)*sin(5ωt+φ5)+Em3*Im7*sin(3ωt)*sin(7ωt+φ7)+... +Em5*Im1*sin(5ωt)*sin(ωt+φ1)+Em5*Im3*sin(5ωt)*sin(3ωt+φ3)+Em5*Im7*sin(5ωt)*sin(7ωt+φ7)+... +Em7*Im1*sin(7ωt)*sin(ωt+φ1)+Em7*Im3*sin(7ωt)*sin(3ωt+φ3)+Em7*Im5*sin(7ωt)*sin(5ωt+φ5)+...)dt) =(1/T)*3*(∫Em1*Im1*(cos(-φ1)-cos(2ωt+φ1))/2+Em3*Im3*(cos(-φ3)-cos(6ωt+φ3))/2+Em5*Im5*(cos(-φ5)-cos(10ωt+φ5))/2+Em7*Im7*(cos(-φ7)-cos(14ωt+φ7))/2+...)dt +∫(Em1*Im3*(cos(-2ωt-φ3)-sin(4ωt+φ3))+Em1*Im5*(cos(-4ωt-φ5)-cos(6ωt+φ5))+Em1*Im7*(cos(-6ωt-φ7)-cos(8ωt+φ7))+... +Em3*Im1*(cos(2ωt-φ1)-cos(4ωt+φ1))+Em3*Im5*(cos(-2ωt-φ5)*sin(8ωt+φ5))+Em3*Im7*(sin(-4ωt-φ7)-cos(10ωt+φ7))+... +Em5*Im1*(cos(4ωt-φ1)-cos(6ωt+φ1))+Em5*Im3*(cos(2ωt-φ3)-cos(8ωt+φ3))+Em5*Im7*(cos(-2ωt)-cos(12ωt+φ7))+... +Em7*Im1*(cos(6ωt-φ1)-cos(8ωt+φ1))+Em7*Im3*(cos(4ωt-φ3)-cos(10ωt+φ3))+Em7*Im5*(cos(2ωt-φ5)-cos(12ωt+φ5))+...)dt) =3*(Em1*Im1*cos(φ1)/2+Em3*Im3*cos(φ3)/2+Em5*Im5*cos(φ5)/2+Em7*Im7*cos(φ7)/2+...) =3*ΣEmn*Imn*cos(φn)/2 (n=1,3,5,7,...) ここで |En|=Emn/√2 |In|=Imn/√2 と置くと Pa=3*Σ|En|*|In|*cos(φn) ということになる。 一方相間電圧の実効値は相電圧の√3倍なので |Vn|=√3*|En| であるので相電圧と線電流で表すと Pa=√3*Σ|Vn|*|In|*cos(φn) ということになる。 P.S 著者はk=0,1,2,...と定義しているが、それだと偶数次の高調波も含まれてしまうので、本来はk=1,3,5,...という奇数の整数列でなければならない。 |
| webadm | 投稿日時: 2009-7-23 20:52 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
非周期波とFourier積分 ここからはちょっと数学的な内容になる。
フーリエ級数 y(t)=Σan*sin(nωt)+b0+Σbn*cos(nωt) (n=1,∞) においてオイラーの公式より sin(nωt)=(e^j*nωt-e^-j*nωt)/2j cos(nωt)=(e^j*nωt+e^-j*nωt)/2 をそれぞれ代入すると y(t)=Σan*(e^j*nωt-e^-j*nωt)/2j+b0+Σbn*(e^j*nωt+e^-j*nωt)/2 =(1/2)*Σ(bn-j*an)*e^j*nωt+b0+(1/2)*Σ(bn+j*an)*e^-j*nωt (n=1,∞) ここで An=(1/2)*(bn-j*an) (n=1,∞) A0=b0 (n=0) A_n=(1/2)*(bn+j*an) (n=-∞,-1) と置くと y(t)=ΣAn*e^j*nωt+ΣA_n*e^-j*nωt (n=0,∞) ということになる。このままだと一般に教えられているフーリエ級数の複素形式とは異なるのだが フーリエ係数 an=(2/T)∫y(t)*sin(nωt)dt bn=(2/T)∫y(t)*cos(nωt)dt を An=(1/2)*(bn-j*an) A_n=(1/2)*(bn+j*an) に代入すると An=(1/2)*((2/T)∫y(t)*cos(nωt)dt-j*(2/T)∫y(t)*sin(nωt)dt) =(1/T)∫y(t)*(cos(nωt)-j*sin(nωt))dt A_n=(1/2)*((2/T)∫y(t)*cos(nωt)dt+j*(2/T)∫y(t)*sin(nωt)dt) =(1/T)∫y(t)*(cos(nωt)+j*sin(nωt))dt ここで再びオイラーの公式より cos(nωt)+j*sin(nωt)=e^j*nωt cos(nωt)-j*sin(nωt)=e^-j*nωt なので An=(1/T)∫y(t)*e^-j*nωtdt A_n=(1/T)∫y(t)*e^j*nωtdt ということになる。 すなわち An(-n)=A_n(n) という関係にあるので y(t)=ΣAn*e^j*nωt+ΣA_n*e^-j*nωt (n=0,∞) =ΣAn*e^j*nωt (n=-∞,0,∞) と書き直すことができる。 ここまでは前準備で、問題は非周期波に拡張するにはどうするかという話。単純に周期Tを∞に引き延ばせばいいのだが数学的に厳密に証明するのは実はかなり面倒くさい。大抵の先生は自分で見つけたようにさらりと説明して終わるはずだ。どうやって証明するかとか導出するかとかは絶対聞いてはいけない。聞いても「この黒板では書ききれない」とか言われてお終いである。ご多分に漏れず著者も説明を省いて天下り的に以下の式を示すに止まっている。 y(t)=(1/2π)∫F(ω)e^jωtdω (ω=-∞,∞) F(ω)=∫y(t)e^-jωtdt (t=-∞,∞) F(ω)をy(t)のFourier変換もしくはFourier積分と呼ぶ。どうみてもフーリエ係数でTを∞に拡張した式に見えるが、Fourier係数と違うのはωの関数になっていて連続的な値を取るということ。Fourier級数の場合は次数である整数nの関数だったので離散的な数列だった。 F(ω)からy(t)を求めることをFourier逆変換、または逆Fourier積分と呼ぶ。 P.S Fourier変換を扱うほとんどの参考書は、その応用の広さを紹介するのにページ数を割くのが精一杯で、Fourier変換の公式の導出方法については省略しているものが多い。導出の根拠無しにその応用を論ずるのはいささか時代に反しているという感は否めない。 Fourier変換の厳密な導出方法はあるに違いないが、ほとんど根拠の土台となる数学的な下ごしらえの部分が多く、結論的に当たり前みたいな形になってしまうと思われる。それらは必ずしもFourier級数の存在を必要としない。結論があっているかどうか証明できればいいのでFourier級数の式が登場しなくても構わないのである。もともとFourier級数もいきなり級数展開式によってほとんどの関数が近似できるという予測からはじまって、それが成り立つ条件を明らかにすることによって数学的に根拠のあるものとなっているので、同じようなものである。 手元の古い参考書には、それぞれFourier変換の公式の導出方法が考え方だけ紹介されている。もちろん厳密ではないが、という但し書き付きである。共通しているのはFourier級数のΣを∫に書き換える際に様々な数学的なトリックが使われている点である。いくつかは天下り的に書き換えてしまっているものがあり、最後まで狐につままれた感じがしてならない。 ここではすべてを紹介しきれないので、参考までに今まで見た中で最も完結かつ数学に素人でも平易にわかるトリックを使ったものを紹介しよう。 Tの定周期波のFourier級数とそのFourier係数は y(t)=ΣAn*e^j*nωt (n=-∞,0,∞) An=(1/T)∫y(t)*e^-j*nωtdt (t=0,T) で表されることは既に学んだ通り。 ここで最初のトリックとして、関数y(t)が時不変であるとすれば An=(1/T)∫y(t)*e-j*nω0tdt (t=-T/2,T/2) が成り立つ。次ぎのトリックとしてω0=2π/TであるのでT→∞とするとω0→Δωとなるとすると An=(Δω/2π)∫y(t)*e-j*nΔωtdt (t=-∞,∞) これをFourier級数の式に代入すると y(t)=Σ{(Δω/2π)∫y(t)*e^-j*nΔωtdt}*e^j*nωt (n=-∞,0,∞) =(1/2π)ΔωΣ∫y(t)*e^-j*nΔωtdt}*e^jωt (n=-∞,∞) ここで新たに最後のトリックとして nΔω=ω と置くと y(t)=(1/2π)ΣΔω∫y(t)*e^-jωtdt}*e^jωt (n=-∞,∞ ω=-∞,∞) Fourier変換を F(ω)=∫y(t)*e^-jωtdt (t=-∞,∞) とすると、 y(t)=(1/2π)ΣΔωF(ω)*e^jωt (n=-∞,∞ ω=-∞,∞) と書き換えることが出来る。 更にT→∞とすればリーマン和は積分と等しくなるので lim ΔωΣF(ω)*e^jωt=∫F(ω)*e^jωtdω (Δω→0) 従ってFourier逆変換は y(t)=(1/2π)∫F(ω)*e^jωtdω (ω=-∞,∞) となる。 Fourier変換、逆変換の式は導出方法のバリエーションの違いによって、上記以外のものがいくつかある。それらを研究してみると一層理解が深まるかもしれない。 |
| webadm | 投稿日時: 2009-7-29 19:13 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
Fourier変換の諸性質 Fourier変換は物理的には任意の波形の時間軸領域と周波数領域との間の相互変換を意味する。
数学的には連続関数の積分で表されるFourier変換を具現化化している装置にはスペクトルアナライザがある。変換したいスペクトル領域の角周波数をスイープ発振させ、それと入力信号を掛け算して得たI/F信号を検波した値を角周波数ωを横軸にプロットするとFourier変換|F(ω)|が現れることになる。 低周波信号領域では十分な分解能がアナログ方式では得にくいので、ナイキストレートで信号をサンプルした数列に対して適用可能な離散Fourier変換が用いられる。一般に計算機で使われている高速Fourier変換は離散Fourier変換を計算機に最適化したアルゴリズムで実装したものである。 天文学の分野では電波望遠鏡の受信信号を高速Fourier変換することによって遠く離れた恒星や銀河のスペクトル分析を行っている。 引き続きFourier変換の便利な諸性質を学んでいくことにする。 (1)線形性 Fourier変換は線形結合が成り立つ。 y(t)=a1*y1(t)+a2*y2(t)+... とするとy(t)のFourier変換は F(ω)=∫y(t)*e^-jωtdt =∫(a1*y1(t)+a2*y2(t)+...)*e^-jωtdt =a1∫(t)*e^-jωtdt+a2∫y2(t)*e^-jωtdt+... =a1*F1(ω)+a2*F2(ω)+... ということになる。 同様に逆変換も F(ω)=a1*F1(ω)+a2*F2(ω)+... とすると y(t)=(1/2π)∫F(ω)*e^jωtdω =(1/2π)∫(a1*F1(ω)+a2*F2(ω)+...)*e^jωtdω =a1*(1/2π)∫F1(ω)*e^jωtdω+a2*(1/2π)∫F2(ω)*e^jωtdω+... =a1*y1(t)+a2*y2(t)+... ということになる。 (2)対称性 F(ω)とy(t)がそれぞれFourier変換対で有る場合 F(ω)=∫y(t)*e^-jωtdt y(t)=(1/2π)∫F(ω)*e^jωtdω F(ω)をFourier逆変換すると (1/2π)∫F(ω)*e^-jωtdω =(1/2π)*F(t) =y(-ω) 従って F(t)=2π*y(-ω) という関係が成り立つ。 (3)時間軸の伸縮 Fourier変換の入力となる関数を時間軸上に伸縮させたら変換結果はどうなるだろうか? 例えば1kHzの正弦波を時間軸上で10倍に引き延ばすと100Hzの正弦波となる、従ってFourier変換結果はそれに反比例した低い方に線スペクトルが遷移するはずだと定性的には予測できる。 Fourier変換の式 F(ω)=∫y(t)*e^-jωtdt において t'=a*t と置くと ωt=(ω/a)*t' 更に ω'=ω/aと置くと ωt=ω't' これらでa>0の場合y(a*t)のFourier変換は (1/a)∫y(t')*e^-jω't'dt' (t'=-∞,∞) =(1/a)*F(ω/a) a<0の場合には時間と逆向きになるので t'=a*t=-|a|*t と置くと (-1/|a|)∫y(t')*e^-jω't'dt' (t'=∞,-∞) =(1/|a|)∫y(t')*e^-jω't'dt' (t'=-∞,∞) =(1/|a|)*F(ω/a) ということになる。 従ってテープに録音した信号を逆再生してFourier変換しても通常に再生したときと同じ結果が得られるということになる。 (4)時間軸と周波数軸の推移 関数y(t)を定数t0だけ右方向に移動した場合はそのFourier変換結果はどうなるか? y(t-t0)のFourier変換は t'=t-t0 と置くと dt'=dt t=t'+t0 なので ∫y(t')*e^-jω(t'+t0)dt' =∫y(t')*e^-jωt'*e^-jωt0dt =t0∫y(t')*e^-jωt'dt*e^-jωt0 =F(ω)*e^-jωt0 ということになる。これは元のスペクトルとe^-jωt0との相関になるることを意味する。元のスペクトルを得るには、相関係数e^tjωt0を乗じて打ち消してやる必要がある。これは電波望遠鏡などのデジタル分光器で行われてる方法である。 同様にωをω0だけ右方向に推移した場合F(ω-ω0)のFourier逆変換は ω'=ω-ω0 と置くと ω=ω'+ω0 dω=dω' なので (1/2π)∫F(ω')*e^j(ω'+ω0)tdω' =(1/2π)∫F(ω')*e^jω'dω'*e^jω0t =y(t)*e^jω0t ということになる。これはω0分だけ周波数変換することを意味する。 (5)微分と積分 y(t)の微分をFourier変換するとどうなるか? ∫{d(y(t))/dt}*e^-jωtdt =∫{d((1/2π)∫F(ω)*e^jωtdω)/dt}*e^-jωtdt =jω∫{(1/2π)∫F(ω)*e^jωtdω)}*e^-jωtdt =jω∫y(t)*e^-jωtdt =jω*F(ω) ということになる。 F(ω)の微分をFourier逆変換するとどうなるか? (1/2π)∫F'(ω)*e^jωtdω (1/2π)∫{d(F(ω))/dω}*e^jωtdω =(1/2π)∫{d(∫y(t)*e^-jωtdt)/dω}*e^jωtdω =(1/2π)∫{(-jt)∫y(t)*e^-jωtdt}*e^jωtdω =(-jt)*(1/2π)∫F(ω)*e^jωtdω =(-jt)*y(t) ということになる。 次にy(t)の積分をFourier変換したらどうなるか? どうすんだこれ? y(t)の積分関数をg(t)とするとそれをtで微分するとその導関数は g'(g)=y(t) ということになる。 従ってg(t)のFourier変換をG(ω)と置くと先の導関数のFourier変換の式から F(ω)=∫y(t)*e^-jωtdt =∫d(g(t))/dt*e^-jωtdt =jωG(ω) 従って G(ω)=∫Y(t)*e^-jωtdt =F(ω)/jω ということになる。いろいろ検索するとy(t)の積分関数の定義の違いによって、これにちょっとおまけがついた式になっているものもあるが、導出方法が説明されているものは無いので大分悩んだ。 F(ω)の積分をFourier逆変換したらどうなるか? これも同様にF(ω)の積分関数をG(ω)とするとその導関数は G'(ω)=F(ω) であるので、先の導関数のFourier逆変換の式からG(ω)のFourier逆変換をg(t)とすると y(t)=(1/2π)∫G'(ω)*e^jωtdω =(-jt)g(t) 従ってF(ω)の積分のFourier逆変換は g(t)=(1/2π)∫G(ω)*e^jωtdω =y(t)/(-jt) =j*y(t)/t ということになる。 このFourier変換とFourier逆変換の対はFourier変換対とよばれ、いろいろな参考書にいくつか有用なものが一覧表で示されていたりする。有る意味で数学の知恵の輪みたいなもので、任意の基本関数の式をネタにしていくらでも問題が出来そうであるが、簡単に解けるのは限られていて、一覧に出ているものも必ずしもその導出方法を示すだけの紙面を割いていないものが多いので鵜呑みは禁物である。自分で導出出来るようになってこそ理解したと言えるだろう。 まだまだ続きがある (6)Parsevalの定理 ほとんどの参考文献でParsevalの定理と呼ばれているが、ParsevalはFourier級数が登場する以前の人でそれまでの級数に関してのものだったのが後にRayleigh卿がFourier級数に適用した際に敬意を表してParsevalの名前を用いたことからRayleighの定理と呼ぶ文献もある。 y(t)とF(ω)の複素共役をそれぞれy*(t)とF*(ω)とするとy*(t)のFourier変換は y*(t)={(1/2π)∫F(ω)*e^jωtdω}* =(1/2π)∫F*(ω)*e^-jωtdω ということになる。 従って ∫|y(t)|^2dt =∫y(t)y*(t)dt =∫y(t){(1/2π)∫F*(ω)*e^-jωtdω}dt =(1/2π)∫F*(ω){∫y(t)*e^-jωtdt}dω =(1/2π)∫F*(ω)F(ω)dω =(1/2π)∫|F(ω)|^2dω ということになる。途中積分項の交換という数式トリックを使用するのがミソ。 これは信号エネルギー密度がFourier変換結果から得られるということを意味する。 (7)畳み込み積分 独立した関数f(t),g(t)のFourier変換をそれぞれF(ω)とG(ω)とすると、それら積をH(ω)とした場合そのFourier逆変換はどうなるか? これはちょうど片方の周波数スペクトルをもう片方の周波数スペクトルでマスクしたような演算になる。つまり任意の周波数範囲だけ抜き出すとか、除去するようなフィルタリング演算に相当する。 (1/2π)∫H(ω)*e^jωtdω =(1/2π)∫F(ω)G(ω)*e^jωtdω ここでF(ω),G(ω)は F(ω)=∫f(t)*e^-jωtdt (t=-∞,∞) G(ω)=∫g(τ)*e^-jωτdτ (τ=-∞,∞) とすると (1/2π)∫F(ω)G(ω)*e^jωtdω =(1/2π)∫{∫f(t)*e^-jωtdt∫g(τ)*e^-jωτdτ}*e^jωtdω =(1/2π)∫{∫f(t)∫g(τ)*e^-jω(t+τ)dτdt}*e^jωtdω ここで積分の変数変換テクニックを使用して t+τ=x とすると τ=x-t dτ=dx と置き換えることができ (1/2π)∫{∫f(t)∫g(x-t)*e^-jωxdxdt}*e^jωtdω =(1/2π)∫{∫∫f(t)g(x-t)dt*e^-jωxdx}*e^jωtdω ここで(f*g)(x)をf(t)とg(t)の合成積(畳み込み積分)と定義すると (f*g)(x)=∫f(t)g(x-t)dt (t=-∞,∞) (1/2π)∫F(ω)G(ω)*e^jωtdω =(1/2π)∫{∫(f*g)(x)*e^-jωxdx}*e^jωtdω 従って H(ω)=∫(f*g)(x)*e^-jωxdx ということになり (1/2π)∫F(ω)G(ω)*e^jωtdω =(1/2π)∫H(ω)*e^jωtdω =h(t) ということになる。 つまりフィルタリングをするにはマスクしたい周波数スペクトルがFourier変換結果となるような応答関数と入力信号を畳み込み積分すればよいことになる。 今度は逆にf(t),g(t)のFourier変換F(ω),G(ω)の畳み込み積分H(ω)をFourier逆変換するとどうなるか? f(t)=(1/2π)∫F(ω)*e^jωtdω g(t)=(1/2π)∫G(ω)*e^jωtdω H(ω)=∫F(ω')G(ω-ω')dω' (ω'=-∞,∞) H(ω)のFourier逆変換は (1/2π)∫H(ω)*e^jωtdω =(1/2π)∫∫F(ω')G(ω-ω')dω'*e^jωtdω 周波数軸シフトのFourier変換対より (1/2π)∫G(ω-ω')*e^jωtdω=g(t)*e^jω't を代入すると =∫F(ω')*e^jω'tdω'*g(t) =2πf(t)g(t) ということになる。む、f(t)g(t)ではないのか? どうなんだこれ? 検算してみよう2πf(t)g(t)のFourier変換は ∫2πf(t)g(t)*e^-jωtdt =∫2π(1/2π)∫F(ω')*e^jω'tdω'g(t)*e^-jωtdt =∫F(ω')∫g(t)e^-j(ω-ω')tdtdω' =∫F(ω')G(ω-ω')dω' =(F*G)(ω) ちゃんとF(ω)とG(ω)の合成積ということになる。あってるじゃないか(´∀` ) もちろん周波数領域での合成積を以下の様に定義すれば2πという係数をFourier変換対から消すことは可能である (F*G)(ω)=(1/2π)∫F(ω')G(ω-ω')dω' いろいろ調べた結果、インターネット上で見ることのできる参考文献の多くはFourier変換の異なる定義式によって混乱を招いており、天下り式にFourier変換対を掲載しているものは誤っているものすらある。特に気をつけないといけないのは、Fourier変換が角周波数(rad/sec)を変数にするのか周波数(Hz)を変数にするのかの違いによって式に2πを含む係数が現れるかどうかが違ってくる。 畳み込み積分、合成積、もしくはConvolutionは別にFourier変換とは独立した概念であるが、信号処理では重要なツールとなる。 ここまではほんの序の口で、連続系Fourier変換は関数解析としては便利だが、実用にするには-∞から∞までの積分を扱うため問題がある。なのでδ関数なる数学上の超関数というトリックを使って離散Fourier変換というものを編み出して、それを使って有限領域かつ離散数列入力に対してFourier変換するというのが普通である。 学校によっては行きなり離散Fourier変換から入るところもある、連続系のFourier変換は離散Fourier変換の式を導出するためにだけ登場すればよいからである。 電気回路理論ではFourier変換よりもラプラス変換が主に用いられる。Fourier変換でも一部の微分方程式を解くのに使用することができるが、ラプラス変換でも出来るのだからそっちに統一した方が教えやすいというものある。 Fourier変換が登場するのは上巻の最後しかない。下巻ではラプラス変換が登場し、ずっとそれが扱われる。フィルターもアナログフィルターしか扱わないのでデジタルフィルターで用いられる離散Fourier変換は登場しない。それらは別途デジタル信号処理という専門分野で学ぶという仕組みである。 著者はどうして下巻で使われることがないFourier変換をここで登場させたのだろうか? これからはデジタル信号処理によるデジタルフィルターが主になるだろうからその前準備として学んで欲しかったのだろうか? もともとこの部分は全体を通して最後の章になるべきところなので、そうなのかもしれない。 デジタル信号処理では数理的な解析に終止するので、ここに登場するような式が出てきても驚かないようにしておくことは重要である。 Fourier変換は突っ込んで研究するときりが無い程奥が深い。特にデジタル信号処理に進むためには、畳み込み積分とδ関数の概念はしっかり身につけないといけない。 Fourier変換を研究すれば微分積分、超関数、複素数、複素解析とかありとあらゆる高等数学を学ぶことになるので、Fourier変換を極めれば自ずと数学を極めることができると言っても過言ではないような気がする。 |
| webadm | 投稿日時: 2009-8-5 9:58 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
線形回路の応答 Fourier変換のところですでに言及した通り、フィルターの様な線形回路へ入力信号を与えた場合にその出力の周波数スペクトルは入力信号のFourier変換とその線形回路のインパルス応答のFourier変換の積となる。
線形回路にインパルス関数δ(t)を加えた際のインパルス応答出力をh(t)とすると、畳み込み積分の式より、入力信号x(t)を与えた場合の出力信号y(t)の関係は以下の通りとなる。 y(t)=(x*h)(t) ここで (x*h)(t)=∫x(t')h(t-t')dt' また出力の周波数スペクトルY(ω)は Y(ω)=X(ω)H(ω) で表される。 この考え方は下巻で学ぶ各種線形回路の解析に共通に使用される。 これで上巻の理論解説は終了。あとは演習をこなすのみ。 |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

