Gan's blog - フォーラム

(1) 2 3 »

投稿者	スレッド
webadm	投稿日時: 2011-7-18 22:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	フィルタ演習問題電気回路のテキストでは割愛される傾向にある古典フィルタ理論の演習問題はやはり数が少ない。最初は理論的な基礎概念の確認、あとは計算問題、最後は理論の際には登場しなかったブリッジ型のフィルタ回路の問題が出されている。

webadm	投稿日時: 2011-7-18 23:12
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	減衰量αの単位 1[Nep]は何[dB]か、また1[dB]は何[Nep]か、という減衰量αの単位変換に関する問題。そもそもそれぞれの減衰量の定義を憶えていないと答えられない問題。変換式を暗記するのは一夜漬けには有効だが意味が無い。良く登場する[dB]の定義は $\begin{eqnarray}<br />10^{\alpha_B}&=&\left\|\frac{P_1}{P_2}\right\|\\<br />\alpha_B&=&log_{10}\left\|\frac{P_1}{P_2}\right\|\\<br />10^{\frac{\alpha_{dB}}{10}}&=&\left\|\frac{P_1}{P_2}\right\|\\<br />\alpha_{dB}&=&10 log_{10}\left\|\frac{P_1}{P_2}\right\|<br />\end{eqnarray}$ ということだった。もともとベル[B]という単位が入力側と出力側の電力の比を常用対数に変換したものとしてあって。それだとちょっと値がちっこ過ぎるので、ベル[B]を10倍したデシベル[dB]という単位を設けたという感じ。小学校で習ったリットル[L]とデシリットル[dL]みたいなものだよね。一方でネイパー[Nep]は $\begin{eqnarray}<br />e^{\alpha_{Nep}}&=&\sqrt{\left\|\frac{P_1}{P_2}\right\|}\\<br />\alpha_{Nep}&=&\frac{1}{2}ln\left\|\frac{P_1}{P_2}\right\|<br />\end{eqnarray}$ したがってこれらの定義式から $\begin{eqnarray}<br />\alpha_{dB}&=&10 log_{10}\left\|\frac{P_1}{P_2}\right\|=10 log_{10}\left( e^{2\alpha_{Nep}}\right)=20\alpha_{Nep}log_{10}\left(e\right)=\frac{20}{ln\left(10\right)}\alpha_{Nep}\\<br />&=&8.686 \alpha_{Nep}\\<br />\alpha_{Nep}&=&\frac{1}{2}ln\left\|\frac{P_1}{P_2}\right\|=\frac{1}{2}ln\left(10^{\frac{\alpha_{dB}}{10}}\right)=\frac{1}{20}\alpha_{dB}ln\left(10\right)=\frac{ln\left(10\right)}{20}\alpha_{dB}\\<br />&=&0.1151 \alpha_{dB}<br />\end{eqnarray}$ という関係が成り立つ。従って1[Nep]は8.686[dB]で1[dB]は0.1151[Nep]ということになる。なんだ簡単じゃないか( ´∀`)

webadm	投稿日時: 2011-7-18 23:53
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	電力と電圧のdB 次は一般的なdBに関する常識を問う問題。 1[μW]を基準にすると1[W]は何[dB]になるか、また1[μV]を基準にすると1[V]は何[dB]か？というもの。よくある引っかけ問題。dBの定義を良く理解している必要がある。元来はdBは電力比の常用対数値であるので、電圧比を扱う場合にはちょっと注意が必要だ。 $\begin{eqnarray}<br />{dB}&=&10 log_{10}\left\|\frac{P_1}{P_2}\right\|=10 log_{10}\frac{1}{10^{-6}}=10 log_{10}10^{6}\\<br />&=&60[dB]<br />\end{eqnarray}$ ということになる。良く高周波回路で出てくるのに1mWを基準にした[dBmW]という単位が登場する。さて電圧の場合はどうしたものだろうか。 dBのちゃんとした定義を探そうとしたら驚愕の事実が発覚。なんと電気学会編の電気工学ハンドブックやオーム社の電子工学ハンドブックにはdBがまったく載っていなかった。完璧なまでにスルーしているのである。おそらくオリジナルのベル研究所の論文とか図書をあたれば良いのだろうけど、ベル研究所はとっくの昔に消滅して今では存在しない。ベル研究所から出ていた出版物も大企業の多くがその時点で廃棄している。通信システム工学ハンドブックにだけはさすがにちょっと載っていた。といってももう注釈欄にたった一行でしか書いてない申し訳程度のもの。 dBはもともと電力比の常用対数であるが、入力と出力のインピーダンスが同一である場合にのみ電圧比や電流比に関して以下が成り立つ $\begin{eqnarray}<br />\alpha_{dB}&=&10 log_{10}\left\|\frac{P_1}{P_2}\right\|\\<br />&=&10 log_{10}\left\|\frac{V_1 I_1}{V_2 I_2}\right\|=10 log_{10}\left\|\frac{V_1^{2}/\cancel{R}}{V_2^{2}/\cancel{R}}\right\|=10 log_{10}\left\|\frac{\cancel{G}V_1^{2}}{\cancel{G}V_2^{2}}\right\|\\<br />&=&10 log_{10}\left\|\frac{V_1^{2}}{V_2^{2}}\right\|=10 log_{10}\left\|\frac{I_1^{2}}{I_2^{2}}\right\|\\<br />&=&20 log_{10}\left\|\frac{V_1}{V_2}\right\|=20 log_{10}\left\|\frac{I_1}{I_2}\right\|<br />\end{eqnarray}$ これは我流だが、ちゃんとした解説はやはり手元にあるベル研究所がかつて出版していた「Transmission Systems for Communications(Fourth Edition)」の邦訳本「通信システム」の第二章に書かれていた。それによるとデシベルの定義は既に承知の通り $\begin{eqnarray}<br />D&=&10 log\left(p_1/p_2\right)\,\,[dB]<br />\end{eqnarray}$ とあり、logは常用対数でp1,p2は同単位の電力値であることから、デシベルは２つの電力値の振幅比を常用対数を１０倍したものということになる。ここで入力と出力が終端された二端子対回路モデルを考える。ベル研究所の記述にはちょっと誤解を招く表現がある（邦訳が不適切なのかもしれない）ためそれはちょっと割愛する。入力と出力のインピーダンスZk=Rk+jXkによって消費される電力pkは $\begin{eqnarray}<br />p_k&=&\frac{E_k^2}{2 R_k\left(1+X_k^{2}/R_{k}^{2}\right)}=\frac{1}{2}R_k I_k^{2}<br />\end{eqnarray}$ と等しいとある。ところでこの式はどうやって導出したのだろうかという疑問がわく。上の回路でのインピーダンスZkで消費される有効電力は入力と出力がそれぞれインピーダンス整合されているとすれば $\begin{eqnarray}<br />p_k&=&\frac{1}{2}\left(\frac{1}{2}\left(E_k \overline{I_k}+\overline{E_k}I_k\right)\right)\\<br />&=&\frac{1}{4}\left(\frac{E_k\overline{E_k}}{\overline{Z_k}}+\frac{\overline{E_k}E_k}{Z_k}\right)\\<br />&=&\frac{1}{4}\left(\frac{Z_k\left\|E_k\right\|^2+\overline{Z_k}\left\|E_k\right\|^2}{\overline{Z_k}Z_k}\right)\\<br />&=&\frac{1}{4}\left(\frac{2 R_k\left\|E_k\right\|^2}{R_k^{2}+X_k^{2}}\right)=\frac{1}{2}\left(\frac{R_k\left\|E_k\right\|^2}{\left\|Z_k\right\|^2}\right)\\<br />&=&\frac{\left\|E_k\right\|^2}{2 R_k\left(1+X_k^{2}/R_k^{2}\right)}=\frac{1}{2}R_k\left\|I_k\right\|^2<br />\end{eqnarray}$ ということだった。従って上記の式を元のデシベルの式に適用すると $\begin{eqnarray}<br />D&=&10 log\left(p_1/p_2\right)=10 log\left(\frac{\frac{\left\|E_1\right\|^2}{2 R_1\left(1+X_1^{2}/R_1^{2}\right)}}{\frac{\left\|E_2\right\|^2}{2 R_2\left(1+X_2^{2}/R_2^{2}\right)}}\right)\\<br />&=&10 log\left(\frac{\left\|E_1\right\|^2}{\left\|E_2\right\|^2}\right)-10 log\left(\frac{R_1}{R_2}\right)-10 log\left(\frac{1+X_1^{2}/R_1^{2}}{1+X_2^{2}/R_2^{2}}\right)\\<br />&=&D_E-D_R-D_X\\<br />D_E&=&20 log\left(\left\|\frac{E_1}{E_2}\right\|\right)=20 log\left(\left\|\frac{V_1}{V_2}\right\|\right)\\<br />D_R&=&10 log\left(\frac{R_1}{R_2}\right)\\<br />D_X&=&10 log\left(\frac{1+X_1^{2}/R_1^{2}}{1+X_2^{2}/R_2^{2}}\right)<br />\end{eqnarray}$ ということになる。今日多くの書物では書かれていない以下のことが書かれている。引用： E1とE2の差がたとえば20dBであるということはいかなる意味であろうか。判断する条件に次ぎの３つの場合があると考えられる。１，Z1=Z2 この場合、DR=DX=0,D=DE=20dBで、その意味は明らかである。２．Z1≠Z2、ただし(X1/R1)=(X2/R2) これはX1=X2=0のときに起こることが多い。DEはdB表示の電圧計で測れるが、指示値よりDRを減じる修正が必要である。３．(X1/R1)≠(X2/R2) R1=R2であっても明らかにZ1≠Z2である。一般には条件３のときはDRとDXの両方を考慮の対象としなければならず、これらをDEから減じることによりDが求まる。条件２および条件３のとき、電圧または電流比をdB単位で表すと、誤解を生じることがある。レベル情報を得たものが、その値が無修正値DEでなくDであることを確認したいときは、上記分類のどのタイプに属するかよく知る必要がある。まったくもって重要かつ大切な上記の事柄が、現在出版されている電気や電子回路の書籍では割愛されている点に正直驚いた。もはや先人の知恵など骨董無用という判断だろうか。こうした背景説明を一切はぶいて都合の良い事柄だけを抜き出すと、通信システム工学ハンドブックや今日のどの教科書にも載っている以下の不親切な定義になってしまう。 $\begin{eqnarray}<br />dB&=&10 log_{10}\left(P_2/P_1\right)\\<br />dB&=&20 log_{10}\left(V_2/V_1\right)<br />\end{eqnarray}$ これじゃまったく先人の考えが伝わってないことは明白である。まあ、残りの問題に対する答えはZ1=Z2であると前提とすれば $\begin{eqnarray}<br />dB&=&20 log_{10}\left(\frac{1}{10^{-6}}\right)=20 log\left(10^{6}\right)\\<br />&=&120[dB]<br />\end{eqnarray}$ ということになる。これも無線測定関係で1μVを基準としたdBμVという単位が存在する。

webadm	投稿日時: 2011-7-19 4:48
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	電力比、電流比これも似たような計算問題。電力比、電流比が二倍の場合、それぞれ何[dB]となるか、またそれは何[Nep]か？というもの。 dBと減衰定数の定義に従って計算すると $\begin{eqnarray}<br />10 log_{10}\frac{P_1}{P_2}&=&10 log_{10} 2=3.01[dB]\\<br />ln\sqrt{\frac{P_1}{P_2}}&=&ln\sqrt{2}=\frac{1}{2}ln 2=0.347[Nep]\\<br />20 log_{10}\frac{V_1}{V_2}&=&20 log_{10} 2=6.02[dB]\\<br />ln\frac{V_1}{V_2}&=&ln 2=0.693[Nep]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2011-7-20 9:12
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	RL並列回路次はやっとフィルタの問題かと思いきや RL並列回路に電流源Iを接続し周波数を変化させたとき、回路の両端の電圧と最大電圧E0との比で与えられる減衰定数の周波数特性を示せ。いきなりRL並列回路。いみわかんね（´Д｀；）この問題は題意をくみ取る問題である。RL並列回路だけではどうみても二端子回路なので入力と出力の区別がない。強いて上げれば電圧と電流の関係が周波数特性をもつぐらい。と思っていたがこういう見方もあるということで感心しきりである。 RL並列回路のLは周波数が0で短絡状態であり周波数が高くなるほどリアクタンスが大きくなりωが無限大でリアクタンス無限大となる（すなわち回路上存在しないのと一緒）。この問題の罠は最大電圧E0の意味である。最初なんのことかさっぱり判らないかったが、著者の回答例をみてやっと納得した。 RL並列回路のインピーダンスの軌跡を描くと、ω=0で原点から始まり、ω=∞でRに至る。その中間はインピーダンスは複素数になりちょうと半円を描くことになる。だからなんだということになるが、インピーダンスが最も大きくなるのはω=∞の時で、その時にRL並列回路に流れる定電流で最も大きな電圧が生じることになる。これがE0の定義だということだ。つまりω=∞の時のRL並列回路のインピーダンスZはRと等しくなる。これとの比から与えられる減衰定数を導けという意味になる。この種の円線図はRが固定でリアクタンスが変化する固定抵抗線と呼ばれる。後に分布定数回路で登場する高周波のインピーダンス整合回路設計に活躍する水橋－スミスチャート（通称スミスチャート）の一部である。さて問題の回路を図で表すとというフィルタ回路とは似てもにつかないのである。著者はこの回路のままで解いているが、違うやり方をしてみよう。へそ曲がりなので定電流源とRの並列回路を等価電圧源回路に置き換えるとちゃんとしたフィルタ回路になるではないか。おそらくこの問題の考案者はこの回路で出題するのではなく、ひとつひねって等価電流源回路に置き直して問題文を作ったのではなかろうかと想像する。どちらも同じ回路であるが、言い換え問題である。この回路は立派なR-∞型構成フィルタと呼ばれる。これなら減衰定数もすんなり見てとれる。題意ではLの両端の最大電圧E0を基準にとあるので、実際には以下のように0-∞型構成フィルタの周波数特性を調べることになる。すなわち入力信号源E0と開放端出力電圧Eの比率の対数をとればいいわけである。なんだ簡単じゃないか( ´∀`) 上の回路図で問題を出されたらあまりに簡単すぎるから少し捻った等価回路で出題したのだろうね。 $\begin{eqnarray}<br />E_0&=&R I\\<br />E&=&\frac{E_0}{R+L s}L s=\frac{E_0}{\frac{R}{L s}+1}\\<br />\alpha&=&20 log_{10}\left\|\frac{E_0}{E}\right\|=20 log_{10}\frac{\left\|E_0\right\|}{\left\|\frac{E_0}{\frac{R}{L s}+1}\right\|}\\<br />&=&20 log_{10}\frac{\cancel{\left\|E_0\right\|}}{\frac{\cancel{\left\|E_0\right\|}}{\sqrt{\frac{R^2}{L^2\omega^2}+1}}}\\<br />&=&20 log_{10}\sqrt{\frac{R^2}{L^2\omega^2}+1}\\<br />&=&10 log_{10}\left(\left(\frac{{\omega_0}}{\omega}\right)^2+1\right)\\<br />\omega_0&=&\frac{R}{L}<br />\end{eqnarray}$ ということになる。著者の解だと減衰定数ではなくゲイン定数を求めている点が大きく異なる。減衰定数なら正の値が減衰で負はゲイン（増幅）である。このあたりがデシベルの定義が曖昧に教えられてきた歴史の弊害がある。そもそもデシベルの考え方からすると入力と出力のインピーダンスが異なっているのでこれは明らかなな誤用である。出力側に電力が伝わらない時点で理論上は0-∞型構成に分離されるが決して実用的な回路ではないことは確か。題意に従って減衰定数をω/ω0に関してプロットするとということになる。すなわち高域通過フィルタというわけだった。 P.S さらなる別解として等価回路から伝送行列を起こせばその開放電圧減衰率(A)からも同じ結果を得ることができる $\begin{eqnarray}<br />F&=&\begin{bmatrix}1 & R\cr 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0\cr \frac{1}{L s} & 1\end{bmatrix}\\<br />&=&\begin{bmatrix}\frac{R}{s\,L}+1 & R\cr \frac{1}{s\,L} & 1\end{bmatrix}\\<br />\alpha&=&20 log_{10}\left\|\frac{R}{s\,L}+1\right\|=20 log_{10}\sqrt{\left(\frac{R}{\omega L}\right)^2+1}\\<br />&=&10 log_{10}\left(\left(\frac{R}{\omega L}\right)^2+1\right)\\<br />&=&10 log_{10}\left(\left(\frac{\omega_0}{\omega}\right)^2+1\right)\\<br />\omega_0&=&\frac{R}{L}<br />\end{eqnarray}$

webadm	投稿日時: 2011-7-25 5:11
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	定K型低域フィルタの設計次の問題は定K型低域フィルタの設計問題。公称インピーダンスR=600[Ω]、遮断周波数f1=10[kHz]の定K形低域フィルタを作り、その減衰特性、位相特性を図示せよ。というもの。著者はフィルタの章の内容および演習問題の出典を明記していないが、たままた手元にある1970年代の古い「電気回路論演習」松元崇著学献社の記述内容を更にコンサイスにまとめ、誘導m形の記述を同様に加筆したたものであることが伺われる。その証拠に例題として本問題とほぼ同じ題意と解答内容の例題が載っている。いずれにせよ定K形フィルタを本来の半回路である逆L字回路しか扱わないという制約が以降の日本のフィルタ設計者の知識体系に大きな構造的な歪みをもたらしているのは否めない。定K形フィルタ＝逆L字回路という図式が学生の頃に刷り込まれてしまっているのである。学生は図書館で古い原典に触れない限り先人の優れた遺産を知らずに社会へ出てしまうことになる。いずれにせよすべての大学で教えるということは不可能なので、何を優先すべきかということで、定K形フィルタの背後にある考えはさておき形骸的な知識（教養）のみを優先したというのが本当だろう。それが自分では何一つ考えない自称技術者を大量生産する結果をもたらしたのは想像に難くない。なんの話だったっけ。ああ、定K形低域フィルタの設計問題ね。このような理由から、逆L字回路しか教えられていない学生にそれ以上を知識や研究を必要とする問題を出すことは許されないので、当然ながら定K形フィルタ＝逆L字形という制約の中で問題を考えることを余技なくされる。それがアマチュア技術者にとってフィルタ＝定K形もしくは誘導m型＝逆L字形回路という狭い見識しか与えない結果になっていることも否めない。本当は違うのだよと、注釈欄に対称T字形回路や対称π形回路をちょっと載せているのは著者の良心の現れであると勝手に解釈しよう。こちらは著者の日本の伝統的なテキストは一切見ずにValkenburgの著書から学ぶというやり方をとったので定K形や誘導m形フィルタは基本は対称T字形や対称π形がプロトタイプで、外部（定抵抗終端）とインピーダンス整合を良くする目的で誘導m形の半回路を両端に使用するということを学んできた。確かにそこまで学ぶのに大変な期間を要したので、それを今の大学の制限された講義時間で教えるのは不可能であるのも理解している。計算機が無かった時代の数式をベースにした解析的アプローチもコンピューターと高度なソフトが使える時代では教えるのは大変だ。教わるほうも大変な抵抗がある。それが基礎力(minimum)だと言ってもなかなか若い時にはわからない。講師だって安い給料でそれ以上の努力は無駄であるとわかっているから何もできない。それだから講師への報酬は生かさず殺さず雀の涙ほどに低く押さえざるを得ないのが現状である。なんの話だっけ。ああ、問題を解かないとね。著者は定K形フィルタの理論で導出した公式を使って素子定数を割り出すアプローチをとっている。それは伝統的ではあるが、そもそも古典フィルタ理論以降では公式というのは意味をもたなくなるばかりか存在すらしなくなる。そこで、古典フィルタ理論以降も有効は方法でアプローチしてみることにしよう。まずは最終的なフィルタが定K形低域通過フィルタの半回路で構成するとすれば、以下の様な回路になる定K形低域通過フィルタの条件は $\begin{eqnarray}<br />\frac{Z_1}{2}2 Z_2&=&Z_1 Z_2=\frac{L}{C}=R^2\\<br />Z_1&=&L s\\<br />Z_2&=&\frac{1}{C s}<br />\end{eqnarray}$ だったことだけは思い出そう。この制約によって公称インピーダンスRとZ1,Z2の関係が定まる。しかしこれだけでは特定のRを持つLとCの組み合わせは無限に存在するので、もうひとつの遮断周波数によってLとCの条件を絞り込む必要がある。定K形フィルタは影像インピーダンスが通過域では実数を減衰域では純虚数をとる性質を利用している。従ってその変化点を影像インピーダンスから見つけ出す必要がある。影像インピーダンスは非対称回路の場合、回路の伝送行列から以下のように求められる $\begin{eqnarray}<br />F&=&\begin{bmatrix}1 & \frac{Z_1}{2}\cr 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0\cr \frac{1}{2 Z_2} & 1\end{bmatrix}\\<br />&=&\begin{bmatrix}\frac{Z_1}{4\,Z_2}+1 & \frac{Z_1}{2}\cr \frac{1}{2\,Z_2} & 1\end{bmatrix}\\<br />Z_{i1}&=&\sqrt{\frac{A B}{C D}}=\sqrt{\frac{\left(\frac{Z_1}{4\,Z_2}+1\right)\left(\frac{Z_1}{2}\right)}{\left(\frac{1}{2\,Z_2}\right)}}=\sqrt{Z_1\,\left( \frac{Z_1}{4\,Z_2}+1\right) \,Z_2}=\sqrt{\frac{Z_1^2}{4}+Z_1 Z_2}\\<br />&=&R\sqrt{\frac{Z_1}{4 Z_2}+1}\\<br />Z_{i2}&=&\sqrt{\frac{D B}{C A}}=\sqrt{\frac{\frac{Z_1}{2}}{\left(\frac{1}{2\,Z_2}\right)\left(\frac{Z_1}{4\,Z_2}+1\right)}}=\sqrt{\frac{\frac{Z_1}{2}}{\frac{Z_1}{8\,Z_2^2}+\frac{1}{2\,Z_2}}}=\sqrt{\frac{Z_1 Z_2}{\frac{Z_1}{4\,Z_2}+1}}\\<br />&=&\frac{R}{\sqrt{\frac{Z_1}{4\,Z_2}+1}}<br />\end{eqnarray}$ Z1=Ls,Z2=1/(Cs)をそれぞれ代入すると影像インピーダンスは $\begin{eqnarray}<br />Z_{i1}&=&R\sqrt{\frac{L s}{4 \frac{1}{C s}}+1}=R\sqrt{\frac{L C s^2}{4}+1}\\<br />Z_{i2}&=&\frac{R}{\sqrt{\frac{L s}{4\,\frac{1}{C s}}+1}}=\frac{R}{\sqrt{\frac{L C s^2}{4}+1}}<br />\end{eqnarray}$ ということになる。従って定常状態ではs=jωと置くことによって $\begin{eqnarray}<br />Z_{i1}&=&R\sqrt{1-\frac{L C \omega^2}{4}}=R\sqrt{\frac{L C}{4}\left(\frac{4}{L C}-\omega^2\right)}\\<br />Z_{i2}&=&\frac{R}{\sqrt{1-\frac{L C \omega^2}{4}}}=\frac{R}{\sqrt{\frac{L C}{4}\left(\frac{4}{L C}-\omega^2\right)}}<br />\end{eqnarray}$ 従って影像インピーダンスが実数と純虚数の境界点となるωが遮断周波数ω0であるので $\begin{eqnarray}<br />\frac{4}{L C}-{\omega}^2&=&0\\<br />\omega&=&\pm\frac{2}{\sqrt{L C}}=\omega_0<br />\end{eqnarary}$ ということになる。題意では角周波数(rad)ではなくkHzであるので遮断周波数f0は $\begin{eqnarray}<br />f_0&=&\frac{\omega_0}{2\pi}=\frac{1}{\pi\sqrt{L C}}<br />\end{eqnarray}$ ということになる。従って、題意の仕様から $\begin{eqnarray}<br />\frac{L}{C}&=&R^2=600^2\\<br />10000&=&\frac{1}{\pi\sqrt{L C}}<br />\end{eqnarray}$ これをLとCに関する連立方程式として解くと $\begin{eqnarray}<br />L&=&\frac{3}{50\,\pi }=0.0191=19.1[mH]\\<br />C&=&\frac{1}{6000000\,\pi }=5.31\cdot 10^{-8}=0.0531[\mu F]<br />\end{eqnarray}$ ということになる。さて難しいのはここからだ、周波数特性をプロットしなければならない。回路の伝送行列から伝達定数θは $\begin{eqnarray}<br />e^{\theta}&=&\sqrt{A D}+\sqrt{B C}=\sqrt{\frac{Z_1}{4\,Z_2}+1}+\sqrt{\frac{Z_1}{2}\left(\frac{1}{2\,Z_2}\right)}=\sqrt{\frac{L s}{4\frac{1}{C s}}+1}+\sqrt{\frac{L s}{4\frac{1}{C s}}}\\<br />&=&\sqrt{\frac{L C s^2}{4}+1}+\sqrt{\frac{L C s^2}{4}}\\<br />&=&\sqrt{1-\frac{\omega^2}{\omega_0^2}}+j\frac{\omega}{\omega_0}\\<br />e^{-\theta}&=&\frac{1}{\sqrt{1-\frac{\omega^2}{\omega_0^2}}+j\frac{\omega}{\omega_0}}=\sqrt{1-\frac{\omega^2}{\omega_0^2}}-j\frac{\omega}{\omega_0}\\<br />cosh\theta&=&\frac{e^{\theta}+e^{-\theta}}{2}=\sqrt{1-\frac{\omega^2}{\omega_0^2}}\,\,\left(\omega\le\omega_0\right)\\<br />&=&j\sqrt{\frac{\omega^2}{\omega_0^2}-1}\,\,\left(\omega\ge\omega_0\right)\\<br />\sinh\theta&=&\frac{e^{\theta}-e^{-\theta}}{2}=j\frac{\omega}{\omega_0}\\<br />\theta&=&ln\left(\sqrt{A D}+\sqrt{B C}\right)=ln\left(\sqrt{1-\frac{\omega^2}{\omega_0^2}}+j\frac{\omega}{\omega_0}\right)\\<br />&=&\frac{ln\left(1\right)}{2}+j\,tan^{-1}\frac{\frac{\omega}{\omega_0}}{\sqrt{1-\frac{\omega^2}{\omega_0^2}}}\,\,\left(\omega\le\omega_0\right)\\<br />&=&ln\left(\sqrt{\frac{\omega^2}{\omega_0^2}-1}+\frac{\omega}{\omega_0}\right)+j\,tan^{-1}\infty\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ 従って周波数特性は２つの解の集合からなり $\begin{eqnarray}<br />\alpha&=&0,\,\,\beta=tan^{-1}\frac{\frac{\omega}{\omega_0}}{\sqrt{1-\frac{\omega^2}{\omega_0^2}}}\,\,\left(\omega\le\omega_0\right)\\<br />\alpha&=&ln\left(\sqrt{\frac{\omega^2}{\omega_0^2}-1}+\frac{\omega}{\omega_0}\right),\,\,\beta=tan^{-1}\infty=\frac{\pi}{2}\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ ということになる。これをプロットするとということになる。定K形フィルタの条件と二端子対回路で学んだ影像パラメータ、それに複素双曲線関数及び逆関数、複素対数関数のことを忘れてなければスクラッチから解析はできることを確認できた。本当は正規化回路(L=1,C=1,R=1を定数として持つプロトタイプ）の周波数特性から周波数変換やインピーダンススケーリングを行うことで要求される公称インピーダンスと遮断周波数を持つフィルタが設計できることを示したかったがそれは読者の課題としよう( ´∀`) (2011/9/4) ２つの区間が解析接続されるように遮断周波数で区間がオーバーラップするように訂正。

webadm	投稿日時: 2011-7-28 4:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	続：定K形低域フィルタの設計次も定K形低域フィルタの問題今度は前問とは逆で、あらかじめ素子定数が与えられている回路の遮断周波数と公称インピーダンスを求める計算問題。上の回路でL=30[mH],C=2[uF]とした場合の遮断周波数f1と公称インピーダンスRを求めよというもの。遮断周波数f1は $\begin{eqnarray}<br />f_1&=&\frac{\omega_0}{2\pi}=\frac{\frac{2}{\sqrt{L C}}}{2\pi}\\<br />&=&\frac{1}{\pi\sqrt{L C}}=\frac{1}{\pi\sqrt{30\cdot 10^{-3}\cdot 2\cdot 10^{-6}}}\\<br />&=&1299[Hz]<br />\end{eqnarray}$ ということになる。公称インピーダンスRは $\begin{eqnarray}<br />Z_1 Z_2&=&\frac{L s}{2}\left(\frac{2}{C s}\right)=\frac{L}{C}=R^2\\<br />R&=&\sqrt{\frac{L}{C}}=\sqrt{\frac{30\cdot 10^{-3}}{2\cdot 10^{-6}}}\\<br />&=&122.5[\Omega]<br />\end{eqnarray}$ ということになる。 P.S この問題を近所のファミレスで計算しようとしたらべき根の計算がどうしても避けられないため難儀した。Gaussとかは計算が得意で筆算で効率よく正確に行う方法を見いだすのが好きだったらしい。確かにべき根とかは簡単には求められない。仕方がないので独自にべき根を机上で求める方法をいろいろ画策してみたがうまくいかない。せめて対数表があればと、今では利用する人もいない対数表のありがたみを実感。√L/Cなどはlog(√L/C)=log(L)/2-log(C)/2となるので対数表があれば足し算と逆引きで答えが得られる。ふと思い出して手元の携帯電話に電卓機能があるのではと思って見てみたらあったはあったが、四則演算しかできない。そういえば昔四則演算しかできない電卓で高度な関数演算を行うテクニックを紹介した本があったのを思い出した。四則演算電卓をそろばん代わりにするやつね。それはそれでGaussの知恵の現代版なのかもしれない。おそらく級数展開近似式とかを使うのかな。そういう意味では公式をいろいろ暗記していないとだめだ。そうだiアプリに電卓があるかもしれないとGoogleで検索してみたが、出てくるのはiPhoneアプリばっかり、iアプリは昔はあったけどサイトが閉鎖されて今は入手困難らしい。iアプリはもう終わってるのね。電卓を買おうか、それとも工夫してGaussを見習うべきか悩むところ。普通は前者なんだろうけどね。計算尺でもいいな。そうだ計算尺ソフトとかもいいかもしれない。アイデアが貧困でだめすぎ（´Д｀；）

webadm	投稿日時: 2011-7-28 8:42
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	続々:定K形低域フィルタの設計次も定K形低域フィルタに関する問題最初の問題に更に仕様が加わっている。公称インピーダンスR=600[Ω]、遮断周波数f1=2[kHz]で、f=4[kHz]における減衰量が40[dB]以上の定K形低域フィルタを構成せよ。というもの。減衰域の特性の周波数における減衰量が指定されている点が加わっている。定K形フィルタの場合、減衰域は同一の定K形フィルタを多段縦続接続することによって減衰量を増すことができる。というか定K形フィルタではそれが限界だ。単体の定K形フィルタ（半回路）の指定周波数での減衰量がわかれば、それを何倍すれば要求の減衰量を満たすかがわかる。最初の設計問題の解から定K形フィルタ（半回路）の減衰域の減衰量αは $\begin{eqnarray}<br />\alpha_{Np}&=&ln\left(\sqrt{\frac{\omega^2}{\omega_0^2}-1}+\frac{\omega}{\omega_0}\right)=ln\left(\sqrt{\frac{\left(\cancel{2\pi} f\right)^2}{\left(\cancel{2\pi} f_1\right)^2}-1}+\frac{\cancel{2\pi} f}{\cancel{2\pi}f_1}\right)\\<br />&=&ln\left(\sqrt{\frac{f^2}{f_1^2}-1}+\frac{f}{f_1}\right)\\<br />\alpha_{dB}&=&20 \frac{\alpha_{Np}}{ln\left(10\right)}=20\frac{ln\left(\sqrt{\frac{4^2}{2^2}-1}+\frac{4}{2}\right)}{ln\left(10\right)}=8.686\cdot ln\left(\sqrt{3}+2\right)\\<br />&=&11.44[dB]<br />\end{eqnarray}$ ということになる。従って少なくとも要求仕様の40[dB]以上を満たすには、四段重ねる必要がある。対称T字形で二段、それに両端に半回路を接続するか、対称π形回路で二段、それに両端に半回路を接続する二通りの構成方法がある。その前にプロトタイプ定K形低域フィルタ(半回路）の素子定数を決めてしまおう。以前の問題でやったのと同様に $\begin{eqnarray}<br />Z_1 Z_2&=&\frac{L \cancel{s}}{\cancel{2}}\frac{\cancel{2}}{C \cancel{s}}=\frac{L}{C}=R^2=600^2\\<br />f_1&=&\frac{\omega_0}{2\pi}=\frac{\frac{\cancel{2}}{\sqrt{L C}}}{\cancel{2}\pi}=\frac{1}{\pi\sqrt{L C}}=2000<br />\end{eqnarray}$ これをLとCについて解くと $\begin{eqnarray}<br />L&=&\frac{3}{10\,\pi }=0.0955=95.5[mH]\\<br />C&=&\frac{1}{1200000\,\pi }=2.65\cdot 10^{-7}=0.265[\mu F]<br />\end{eqnarray}$ ということになる。従って回路構成としては二通りありということになる。著者の解では片方しか示されていない。

webadm	投稿日時: 2011-7-28 20:30
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	定K形高域フィルタの設計次も定K形フィルタの問題。今度は高域フィルタね。公称インピーダンスR=600[Ω],遮断周波数fh=60[kHz]の定K形高域フィルタを作り、その減衰特性、位相特性を示せ。というもの。定K形の低域フィルタと高域フィルタというのは数学的には同形。遮断周波数を中心にして周波数特性の座標軸の0と∞を逆にする変数変換で単射かつ全射な関係。減衰量を複素周波数sの関数とするなら、変数sを1/sにすると0が∞になるし∞が0になるので低域フィルタが高域フィルタになる。低域フィルタのZ1=Ls,Z2=1/Csが高域フィルタではZ1=1/Cs,Z2=Lsとなることで、Z1/2=1/2Cs,2Z2=2Lsへと変わる。遮断周波数は影像インピーダンスの式のZ1,Z2を高域フィルタのそれで置き換えると $\begin{eqnarray}<br />Z_{i1}&=&R\sqrt{\frac{Z_1}{4 Z_2}+1}=R\sqrt{\frac{\frac{1}{C s}}{4 L s}+1}=R\sqrt{\frac{1}{4 L C s^2}+1}\\<br />&=&R\sqrt{\frac{1}{4 L C}\left(4 L C-\frac{1}{\omega^2}\right)}\\<br />Z_{i2}&=&\frac{R}{\sqrt{\frac{Z_1}{4 Z_2}+1}}=\frac{R}{\sqrt{\frac{\frac{1}{C s}}{4 L s}+1}}=R\frac{R}{\sqrt{\frac{1}{4 L C s^2}+1}}\\<br />&=&\frac{R}{\sqrt{\frac{1}{4 L C}\left(4 L C-\frac{1}{\omega^2}\right)}}<br />\end{eqnarray}$ ということになる。従って影像インピーダンスが実数と純虚数の境界をとる遮断周波数fhは $\begin{eqnarray}<br />4 L C-\frac{1}{\omega^2}&=&0\\<br />\omega&=&\frac{1}{2\sqrt{L C}}=\omega_0\\<br />f_h&=&\frac{\omega_0}{2\pi}=\frac{\frac{1}{2\sqrt{L C}}}{2\pi}\\<br />&=&\frac{1}{4\pi\sqrt{L C}}<br />\end{eqnarray}$ ということになる。従って素子定数は $\begin{eqnarray}<br />\frac{Z_1}{\cancel{2}}\cancel{2} Z_2&=&Z_1 Z_2=\frac{1}{C \cancel{s}}L \cancel{s}=\frac{L}{C}=R^2=600^2\\<br />f_h&=&\frac{1}{4\pi\sqrt{L C}}=60000<br />\end{eqnarray}$ これをL,Cに関して解くと $\begin{eqnarray}<br />L&=&\frac{1}{400\,\pi }=7.96\cdot 10^{-4}=0.796[mH]\\<br />C&=&\frac{1}{144000000\,\pi }=2.21\cdot 10^{-9}=0.00221[\mu F]<br />\end{eqnarray}$ ということになる。周波数特性は減衰量が丁度低域フィルタでのω/ω0がω0/ωと逆数に置き換えた形になることから $\begin{eqnarray}<br />\theta&=&ln\left(\sqrt{A D}+\sqrt{B C}\right)=ln\left(\sqrt{1-\frac{\omega_0^2}{\omega^2}}+j\frac{\omega_0}{\omega}\right)\\<br />&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right)+j\,tan^{-1}\infty\,\,\left(\omega\le\omega_0\right)\\<br />&=&\frac{ln\left(1\right)}{2}+j\,tan^{-1}\frac{\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ 従って減衰定数及び位相定数は２つの解の集合から成り $\begin{eqnarray}<br />\alpha&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega}-1}+\frac{\omega_0}{\omega}\right),\,\,\beta=\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)\\<br />\alpha&=&0,\,\,\beta=tan^{-1}\frac{\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}=tan^{-1}\frac{1}{\sqrt{\frac{\omega^2}{\omega_0^2}-1}}\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ ということになる。む、著者の解とで位相定数の極性が異なっている。他の国内の古い参考書でも著者の解と同じく位相は負の値をとっている。Valkenburgの著書ではT字形回路だが位相は正の値をとっている点で真っ向から対立する。どっちなんだ。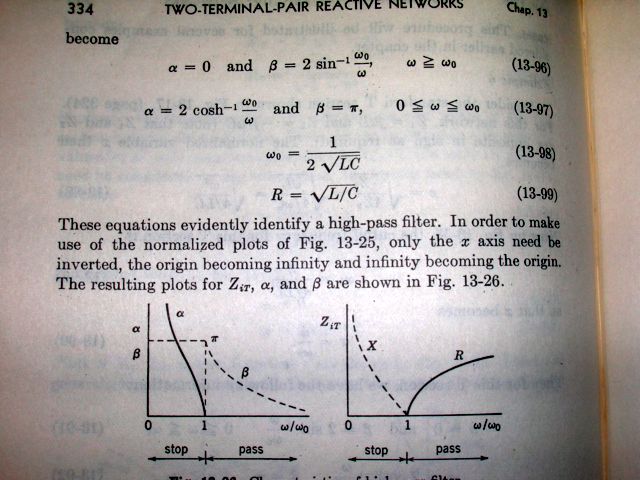国内の古い参考書はまったくといって同じやり方で定K形高域フィルタの位相定数の極性を判定している（「第一級無線技術士用　電気回路（下巻）」室住　熊三著）どうやらこちらの影像伝達定数の導出に問題があるようだ。 $\begin{eqnarray}<br />e^{\theta}&=&\sqrt{A D}+\sqrt{B C}=\sqrt{\frac{Z_1}{4\,Z_2}+1}+\sqrt{\frac{Z_1}{2}\left(\frac{1}{2\,Z_2}\right)}\\<br />&=&\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}\\<br />e^{-\theta}&=&\frac{1}{\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}}=\frac{\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}}{\left(\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}\right)\left(\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}\right)}\\<br />&=&\sqrt{\frac{Z_1^2}{4 R^2}+1}-\sqrt{\frac{Z_1^2}{4 R^2}}\\<br />cosh\theta&=&\frac{e^{\theta}+e^{-\theta}}{2}=\sqrt{\frac{Z_1^2}{4 R^2}+1}=\sqrt{1-\frac{1}{4 \omega^2 C^2 R^2}}\\<br />&=&\sqrt{1-\frac{1}{4 C\cancel{^2} \frac{L}{\cancel{C}}}}=\sqrt{1-\frac{1}{4 \omega^2 L C}}\\<br />&=&\sqrt{1-\frac{\omega_0^2}{\omega^2}}\\<br />sinh\theta&=&\frac{e^{\theta}-e^{-\theta}}{2}=\sqrt{\frac{Z_1^2}{4 R^2}}=\frac{Z_1}{2 R}=\frac{\frac{1}{j\omega C}}{2 \sqrt{\frac{L}{C}}}\\<br />&=&-j\fra{1}{2\omega \sqrt{L C}}\\<br />&=&-j\frac{\omega_0}{\omega}<br />\end{eqnarray}$ βが負の値としている教科書では上のように導出している。sinhθが負の純虚数を取ることが重要だ。こんな導出の手順の違いだけで結果が大きく違ってしまう。Valkenburgも弘法も筆の誤りで半世紀前に同じミスを犯している。人のことは言えないが。これで減衰定数と位相定数を導き直すと $\begin{eqnarray}<br />sinh\left(\alpha+j\beta\right)&=&sinh\alpha\,cos\beta+j\,cosh\alpha\,sin\beta=-j\frac{\omega_0}{\omega}\\<br />conh\alpha\,sin\beta&=&-\frac{\omega_0}{\omega}<br />\end{eqnarray}$ 従って減衰域ではcoshα>0であるのでsinβ<0でなければならない従ってβは負の値を取ることになる $\begin{eqnarray}<br />\theta&=&\alpha+j\beta\\<br />tanh\,\theta&=&\frac{sinh\,\theta}{cosh\,\theta}=\frac{sinh\left(\alpha+j\beta\right)}{cosh\left(\alpha+j\beta\right)}\\<br />&=&\frac{sinh\,\alpha\,cos\,\beta+j\,cosh\,\alpha\,sin\,\beta}{cosh\,\alpha\,cos\,\beta+j\,sinh\,\alpha\,sin\,\beta}\\<br />&=&\frac{\left(sinh\,\alpha\,cos\,\beta+j\,cosh\,\alpha\,sin\,\beta\right)\left(cosh\,\alpha\,cos\,\beta-j\,sinh\,\alpha\,sin\,\beta\right)}{\left(cosh\,\alpha\,cos\,\beta+j\,sinh\,\alpha\,sin\,\beta\right)\left(cosh\,\alpha\,cos\,\beta-j\,sinh\,\alpha\,sin\,\beta\right)}\\<br />&=&\frac{cosh\alpha \,sinh\alpha+j\,cos\beta \,sin\beta}{{sinh\alpha }^{2}\,{sin\beta }^{2}+{cosh\alpha }^{2}\,{cos\beta }^{2}}\\<br />&=&\frac{sinh\,2\alpha+j\,sin\,2\beta }{cos\,2\beta +cosh\,2\alpha }<br />\end{eqnarray}$ 減衰域では影像インピーダンスは純虚数となるためtanhθは実数となる。従ってtanhθの分子の式は実数でなければならないので虚数項は０でなければならない $\begin{eqnarray}<br />sin\,2\beta&=&0\\<br />2\beta&=&\pm\,n\pi\,\left(n=1,2,\cdots\right)\\<br />\beta&=&\pm\,\frac{n\pi}{2}\,\left(n=1,2,\cdots\right)<br />\end{eqnarray}$ 従ってβ=±π/2ということになるが、先の条件でβは負でなければならないためβ=-π/2ということになる。従って減衰域での減衰定数はcoshαから $\begin{eqnarray}<br />cosh\alpha\,sinh\beta&=&cosh\alpha\left(-1\right)=-\frac{\omega_0}{\omega}\\<br />\alpha&=&cosh^{-1}\left(-\frac{\omega_0}{\omega}\right)=cosh^{-1}\frac{\omega_0}{\omega}\\<br />\beta&=&-\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)\\<br />\end{eqnarray}$ ということになり、一方通過域では減衰定数α=0となるので位相定数は $\begin{eqnarray}<br />sinh\left(\alpha+j\beta\right)&=&sinh\alpha\,cos\beta+j\,cosh\alpha\,sin\beta=-j\frac{\omega_0}{\omega}\\<br />conh\alpha\,sin\beta&=&-\frac{\omega_0}{\omega}\\<br />sin\beta&=&-\frac{\omega_0}{\omega}\\<br />\beta&=&sin^{-1}\left(-\frac{\omega_0}{\omega}\right)=-sin^{-1}\frac{\omega_0}{\omega}\\<br />\alpha&=&0\,\,\left(\omega\ge\omega_0\right)<br />\end{eqnarray}$ というのが正解だった。古典フィルタ理論あなどるべからず。今回は日本の古い参考書を評価したい。グラフもプロットし直すとということだった。あえて最初の間違った解法は後学のために残しておこう。 P.S ちょっと納得が行かないので最初のアプローチでやり直してみたところ $\begin{eqnarray}<br />e^{\theta}&=&\sqrt{A D}+\sqrt{B C}=\sqrt{\frac{Z_1^2}{4 R^2}+1}+\sqrt{\frac{Z_1^2}{4 R^2}}=\frac{Z_1}{2 R}\sqrt{1+\frac{4 R^2}{Z_1^2}}+\frac{Z_1}{2 R}\\<br />&=&-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}-j\frac{\omega_0}{\omega}\\<br />&=&cosh\theta+sinh\theta\\<br />cosh\theta&=&-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}\\<br />sinh\theta&=&-j\frac{\omega_0}{\omega}\\<br />\theta&=&\alpha+j\beta=ln\left(-j\frac{\omega_0}{\omega}\sqrt{1-\frac{\omega^2}{\omega_0^2}}-j\frac{\omega_0}{\omega}\right)\\<br />&=&\frac{ln\left(1\right)}{2}+j\,tan^{-1}\frac{-\frac{\omega_0}{\omega}}{\sqrt{1-\frac{\omega_0^2}{\omega^2}}}\,\,\left(\omega\ge\omega_0\right)\\<br />&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right)+j\,tan^{-1}-\infty\,\,\left(\omega\le\omega_0\right)\\<br />\alpha&=&0,\,\,\beta=-tan^{-1}\frac{1}{\sqrt{\frac{\omega^2}{\omega_0^2}-1}}\,\,\left(\omega\ge\omega_0\right)\\<br />\alpha&=&ln\left(\sqrt{\frac{\omega_0^2}{\omega^2}-1}+\frac{\omega_0}{\omega}\right),\,\,\beta=tan^{-1}-\infty=-tan^{-1}\infty=-\frac{\pi}{2}\,\,\left(\omega\le\omega_0\right)<br />\end{eqnarray}$ ちゃんとできたじゃないか( ´∀`) べき根の中が正になるか負になるかで対数変換した結果が二通りに分岐してしまうのが混乱を招いている。最初にZ1^2/(4R^2)をべき根から出して後で記号変換するのがトリックだった。先に記号変換すると正しい結果が得られないという罠だった。これを正解としよう。 (2011/9/4) 解析接続するためにω0で２つの区間がオーバーラップするように訂正。

webadm	投稿日時: 2011-7-29 8:25
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	続：定K形高域フィルタの設計次も定K形高域フィルタの計算問題前問のような定K形高域フィルタでL=4[mH],C=0.3[uF]とした場合の遮断周波数fhと公称インピーダンスRを求めよ。というもの。これは落としたらだめだろうという易しい問題。定K形高域フィルタの公式を憶えているなら $\begin{eqnarray}<br />fn&=&\frac{\omega_0}{2\pi}=\frac{\frac{1}{2\sqrt{L C}}}{2\pi}=\frac{1}{4\pi\sqrt{L C}}\\<br />&=&\frac{1}{4\pi\sqrt{4\cdot 10^{-3} 0.3\cdot 10^{-6}}}=2297[Hz]\\<br />R&=&\sqrt{\frac{L}{C}}=\sqrt{\frac{4\cdot 10^{-3}}{0.3\cdot 10^{-6}}}=115.5[\Omega]<br />\end{eqnarray}$ ということになる。

(1) 2 3 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を