| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-7-18 23:42 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
ひずみ波のFourier級数展開 これまでの交流回路理論では交流は単一周波数の正弦波であることを前提としてきた。
実際には物理的機械的な要因によって発電機の起電力は理想的な正弦波ではなく、変圧器も磁性体の非線形性(ヒステリンシス効果)から正弦波を入れても出力は歪んでしまう。 従って実務ではひずんだ交流信号を扱う必要が出てくる。 一方でオーディオ信号の増幅回路ではひずみは大敵なのでいかに歪まないようにするか苦心する。オーディオアンプの性能のひとつとしてひずみ率があり、それは入力信号に無ひずみの正弦波信号を入力し出力信号に含まれる高調波ひずみレベルの比率を測定することによって行われるのは承知の通り。 周期T=2π/ωを持つひずみ波は以下のようにFourier級数で表すことができる。 y(t)=Σan*sin(nωt)+b0+Σbn*cos(nωt) (n=1,∞) ここでan,b0,bnはFourier係数とよばれ以下で与えられる。 an=(2/T)∫y(t)*sin(nωt)dt (t=0,∞) b0=(1/T)∫y(t)dt (t=0,∞) bn=(2/T)∫y(t)*cos(nωt)dt (t=0,∞) また An=sqrt(an^2+bn^2) θn=tan^-1(bn/an) を用いると以下の様に正弦はのみの級数として表される。 y(t)=b0+ΣAn*sin(nωt+θn) (n=1,∞) b0をひずみ波の直流分、A1*sin(ωt+θ1)を基本波、An*sin(nωt+θn)を第n高調波と呼ぶ。これらの正弦波の集合を周波数スペクトルと呼ぶ。 という感じで天下り的に示されてもなんのことかさっぱり理解できないと思う。 これらは集大成されたFourier級数の総まとめ的な内容であり、それを導出する過程は説明されていない。 なのでひとつひとつオリジナルのアイデアから考え直してみよう。 WikipediaによればFourierが最初に発見した三角関数級数は以下のようなものだった y(t)=Σ((-k)^k/(2*k+1))*cos((2*k+1)*x) (k=0,∞) これを実際にk=0,3までの項でプロットしてみよう。 wxplot2d([-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$ 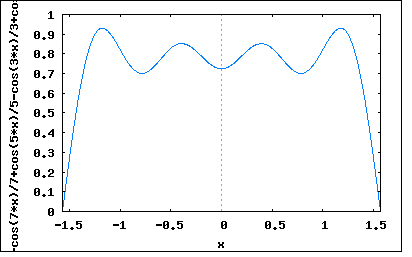 むむ、何やら台形の形をしている。 更に項数を増やしてk=0,7でプロットしてみよう。 wxplot2d([-cos(15*x)/15+cos(13*x)/13-cos(11*x)/11+cos(9*x)/9-cos(7*x)/7+cos(5*x)/5 -cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$  大分台形らしくなってきた。最高値は平坦になるまで収束するのだろうか? 更にk=0,11でプロットしてみよう。 wxplot2d([-cos(23*x)/23+cos(21*x)/21-cos(19*x)/19+cos(17*x)/17-cos(15*x)/15+cos(13*x)/13 -cos(11*x)/11+cos(9*x)/9-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)], [x,-%pi/2,%pi/2])$ 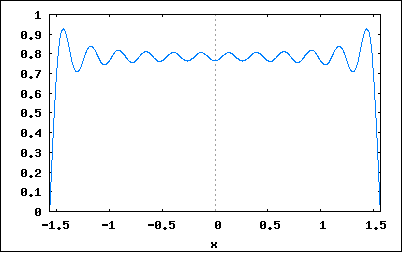 どうやら段々と平坦になってきているのは確か。 これを範囲を広げてプロットしてみると 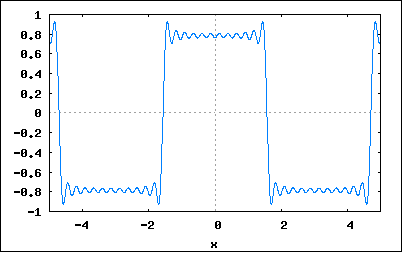 典型的な矩形波の繰り返し波形が見えてくる。 おそらくFourierはわくわくしながら色々な関数を試してみたに違いない、その中でほどよく収束する区間と収束しない区間があるのを認めざるを得ず、それがどうした条件でそうなるのかは独力で明らかにすることはできなかったと思われる。それが後生に研究課題を多く提供した点は誠実な学者としての誠意である。 後にFourier級数を機械的にプロットする装置を作った人が居て、やはり最初に矩形波をプロットさせたところ不連続点でプロッタが激しく振動を繰り返すという怪現象に見舞われた。それは後にギブスが数学的に証明したギブス現象と呼ばれるもので、関数の不連続点では収束せずにアンダーシュートとオーバーシュートが生じるというものである。 先のプロット画像でも急激に値が変化する点ではオーバーシュートとアンダーシュートが顕著であることからも確認できる。 そんな訳ありではあるが、近似というレベルでは十分実用になる範囲のものである。工学的には細かい誤差を追求するよりもいかに手軽に近似解が得られるかが重要である。 そこで話を本論に戻そう。 天下り式にFourier係数の定義が示されているが、a0が無いのは何故だろう? 考えてみればわかるが本来は y(t)=Σan*sin(nωt)+Σbn*cos(nωt) (n=0,∞) と表すのがシンプルだが n=0の場合 y(t)=a0*sin(0)+b0*cos(0) (n=0) ということになる。sin(0)=0、cos(0)=1なので y(t)=b0 ということになりa0の項は消える。 いろいろな本ではsinとcosの順番が入れ替わっていたりするものがあったり、数学系の本では直流分に1/2という係数がついているものがある。 それ以前に著者のFourier係数の式がどうやって導出されたのか気になる。 ここで以前に入手した回路網解析の古書を参考にして検証してみよう。 Fourier係数の式を導出するには前出のFourier級数の式を最長周期で積分する y(t)=Σan*sin(nωt)+Σbn*cos(nωt) (n=0,∞) 最長周期はt=0〜Tとすると ∫y(t)dt=Σan*∫sin(nωt)dt+Σbn*∫cos(nωt)dt (n=0,∞ ωt=0,T) ここでn=0に限定すると ∫y(t)dt=∫b0*dt (t=0,T) =b0*T 従って b0=(1/T)∫y(t)dt (ωt=0,T) ということになる。 次ぎにn=0以外でのanとbnを導く必要がある。 n=奇数に限定すると ∫y(t)dt=an*∫sin(nωt)dt (n=奇数 t=0,T) 両辺にsin(nωt)を乗じると ∫y(t)*sin(nωt)dt =an*∫sin(nωt)^2dt an*∫sin(nωt)^2dt=an*∫(1-cos(nωt)^2)dt =an*∫(1-(1+cos(2nωt))/2)dt =an*∫(1/2-cos(2nωt)/2)dt =an*T/2 従って an=(2/T)*∫y(t)*sin(nωt)dt ということになる。 同様にbnも n=偶数に限定すると ∫y(t)dt=bn*∫cos(nωt)dt (n=偶数 ωt=0,T) 両辺にcos(nωt)を乗じると ∫y(t)*cos(nωt)dt =bn*∫cos(nωt)^2dt =bn*∫cos(nωt)^2dt =bn*∫(1-sin(nωt)^2)dt =bn*∫(1-(1-cos(2nωt))/2)dt =bn*∫(1/2+cos(2nωt)/2)dt =bn*T/2 従って bn=(2/T)*∫y(ωt)*cos(nωt)dt ということになる。 youtubeとかで見ることが出来るMITの数学の講義の中にFourier級数というのがあり、見てみたら、信号が任意の正弦波の合成というところから出発している。 ちょうど著者の説明と逆順にたどることになる。 y(t)=ΣAn*sin(nωt+θn) (n=0,∞) n=0の時 y(t)=A0*sin(θ0) これをb0と置くと b0=A0*sin(θ0) ということになる。 また三角関数の合成定理から sin(nωt+θn)=sin(nωt)*cos(θn)+cos(nωt)*sin(θn) 従って y(t)=b0+ΣAn*(sin(nωt)*cos(θn)+cos(nωt)*sin(θn)) (n=1,∞) =b0+ΣAn*sin(nωt)*cos(θn)+ΣCn*cos(nωt)*sin(θn) ここで an=An*cos(θn) bn=An*sin(θn) と置くと y(t)=Σan*sin(nωt)+b0+Σbn*cos(nωt) ということになり最初の式が導かれることになる。 また sqrt(an^2+bn^2) =sqrt(An^2*cos(θn)^2+An^2*sin(θn)^2) =An tan(θn) =sin(θn)/cos(θn) =(bn/An)/(an/An) =bn/an 従って θn =tan^-1(bn/an) ということになる。 まずはこの程度の理解に止めておこう。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2009-7-18 22:32 |
| » |
webadm | 2009-7-18 23:42 |
| |
webadm | 2009-7-19 19:27 |
| |
webadm | 2009-7-20 0:32 |
| |
webadm | 2009-7-22 10:39 |
| |
webadm | 2009-7-22 20:43 |
| |
webadm | 2009-7-22 21:04 |
| |
webadm | 2009-7-23 20:52 |
| |
webadm | 2009-7-29 19:13 |
| |
webadm | 2009-8-5 9:58 |
| 投稿するにはまず登録を | |

