| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-7-19 19:27 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3093 |
特殊な形のひずみ波 大概の繰り返し波形はフーリエ級数で近似できるということは理解できたが、実際に特定の繰り返し波形をフーリエ級数に展開しようとするとフーリエ係数を決定するのがやっかいである。
いくつかに特殊なケースがあり、必要なフーリエ係数も限定されることが知られている。 (1)対称波の場合 対称波とは最短繰り返し周期(T)の半周期毎に信号が極性反転して繰り返すもの。 y(t+T/2)=-y(t) が成立する場合にはフーリエ級数は以下の様に限定される。 a2m+1=(4/T)∫y(t)*sin((2m+1)*ωt)dt (m=0,1,2,... t=0,T/2) b2m+1=(4/T)∫y(t)*cos((2m+1)*ωt)dt (m=0,1,2,... t=0,T/2) a2m=b2m=b0=0 すなわち奇数次(1,3,5,...)の高調波のみの三角関数級数は対称波になるという。 (2)奇関数の場合 時間0を境にそれ以前の半周期とそれ以降の半周期とで象限を180度反転したような関数は奇関数と呼ばれる。 y(t)=-y(-t) この場合フーリエ係数は an=(4/T)∫y(t)*sin(nωt)dt (t=0,T/2) b0=bn=0 すなわちsin級数のみのフーリエ級数は奇関数ということになる。 b0=0なので (3)偶関数の場合 最短繰り返し周期(T)の半周期を境にして鏡に映したように前半と後半の周期の波形が対称な関数を偶関数と呼ぶ。 y(t)=y(-t) an=0 b0=(2/T)∫y(t)dt (t=0,T/2) bn=(4/T)∫y(t)*cos(nωt)dt (t=0,T/2) すなわちcos級数のみのフーリエ級数は偶関数であると言える。 偶関数の場合のみb0≠0のケースがあることになる。 しかし良く考えると、周期の基点をどこにするかによっては対称波や奇関数、偶関数になったりする気がする。 実際にプロットしてみようと思うと、計算が結構面倒なことがわかる。三角関数と関数の積を積分しないといけない。この操作は特定の高調波との相関係数を求めることを意味する。 実際にそれぞれの簡単な波形グラフを元にフーリエ級数を計算してみよう。 上の様な矩形波を考えてみよう。見ると明らかに偶関数であると同時に対称波でもある。 y(t)の値は -V (ωt=-π〜-π/2) V (ωt=-π/2〜π/2) -V (ωt=π/2〜π) という値を取る。 従ってフーリエ係数は b0=(2/T)∫y(t)dt (t=0,T/2) =(2/T)*(∫Vdt+ (t=0,T/4) ∫-Vdt) (t=T/4,T/2) =(2/T)*(T/4-T/4) =0 bn=(4/T)∫y(t)*cos(nωt)dt (t=0,T/2) =(4/T)*(∫V*cos(nωt)dt+ (t=0,T/4) ∫-V*cos(nωt)dt) (t=T/4,T/2) =(4*V/T)*([sin(nωt)]- (t=0,T/4) [sin(nωt)]) (t=T/4,T/2) =(4*V/T)*(sin(nωT/4)/nω-(sin(nωT/2)-sin(nωT/4))/nω) =(4*V/nωT)*(2*sin(nωT/4)-sin(nωT/2)) (n≠0) ここで T=2π/ω を代入すると bn=(2*V/nπ)*(2*sin(nπ/2)-sin(nπ)) (n≠0) =(4*V/nπ)*sin(nπ/2) すなわち bn=(4*V/(nπ)) (n=1,5,9,...) bn=(-4*V/(nπ)) (n=3,7,11,...) bn=0 (n=2,4,6,...) ということになる。三角関数の各定積分はMaximaを使って求めた。 従って y(t)=(4*V/π)*(cos(ωt)-(1/3)*cos(3*ωt)+(1/5)*cos(5*ωt)-(1/7)*cos(7*ωt)+...) ということになる。 これをプロットしてみると。 wxplot2d([(4*(-cos(7*x)/7+cos(5*x)/5-cos(3*x)/3+cos(x)))/%pi], [x,-2*%pi,2*%pi])$ 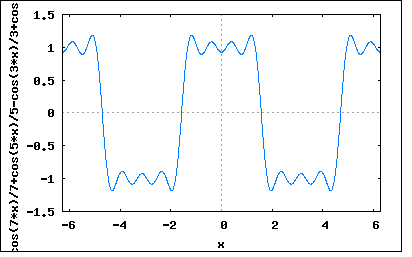 近似な波形が合成されるのが確認できた。三角関数の定積分を求めるのが面倒だ。 今度は同様に奇関数についてやってみよう。 上のような奇数関数な三角波をフーリエ級数に展開してみよう。 奇関数なのでt=0〜T/2の範囲でy(t)は (2*V/π)*ωt (t=0〜T/4) (2*V/π)*(π-ωt) (t=T/4〜T/2) をとる。 従ってフーリエ係数は an=(4/T)∫y(t)*sin(nωt)dt (t=0,T/2) =(4/T)*(∫(2*V/π)*ωt*sin(nωt)dt+ (t=0,T/4) ∫(2*V/π)*(π-ωt)*sin(nωt)dt) (t=T/4,T/2) =(4/T)*(2*V/π)*(∫ωt*sin(nωt)dt (t=0,T/4) +∫(π-ωt)*sin(nωt)dt (t=T/4,T/2) =(4/T)*(2*V/π)*(4*sin(nωT/4)-nωT*cos(nωT/4))/(4*n^2*ω) -(4*sin(nωT/2)-2*nωT*cos(nωT/2)+4*nπ*cos(nωT/2)-4*sin(nωT/4)+nωT*cos(nωT/4)-4*nπ*cos(nωT/4))/(4*n^2*ω))) =(4/T)*(2*V/π)*(-(2*sin(nωT/2)-nωT*cos(nωT/2)+2*nπ*cos(nωT/2)-4*sin(nωT/4)+nωT*cos(nωT/4)-2*nπ*cos(nωT/4))/(2*n^2*ω)) ここで T=2π/ω を代入すると an =(2*ω/π)*(2*V/π)*(4*sin(nπ/2)-2*sin(nπ))/(2*n^2*ω) =(4*V/π^2)*(2*sin(nπ/2)/n^2) (n≠0) ということになる。すなわち an=(8*V/π^2)*(1/n^2) (n=1,5,9,...) an=(8*V/π^2)*(-1/n^2) (n=3,7,11,...) an=0 (n=2,4,6,...) ということになる。 従ってフーリエ級数展開は y(t)=(8*V/π^2)*(sin(ωt)-(1/3^2)*sin(3*ωt)+(1/5^2)*sin(5*ωt)-...) ということになる。 プロットしてみると wxplot2d([(8*(sin(5*x)/25-sin(3*x)/9+sin(x)))/%pi^2], [x,-2*%pi,2*%pi])$  次数は少なくても十分三角波を近似していることがわかる。 相変わらず三角関数の定積分は面倒なのでMaximaで求めた。 今日はこのくらいにしておこう。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2009-7-18 22:32 |
| |
webadm | 2009-7-18 23:42 |
| » |
webadm | 2009-7-19 19:27 |
| |
webadm | 2009-7-20 0:32 |
| |
webadm | 2009-7-22 10:39 |
| |
webadm | 2009-7-22 20:43 |
| |
webadm | 2009-7-22 21:04 |
| |
webadm | 2009-7-23 20:52 |
| |
webadm | 2009-7-29 19:13 |
| |
webadm | 2009-8-5 9:58 |
| 投稿するにはまず登録を | |

