| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-9-6 19:57 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3087 |
【41】直流分を含まない偶数波 次ぎの問題は直流分を含まない偶数波に関する興味深い問題。
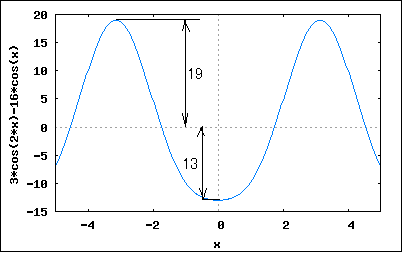 「直流分を含まない図のような波形の正弦波からのずれが主として第二高調波によるものであるとき、第二高調波と基本波の大きさの比を求めよ。」 波形を見ると偶数波であることは一目瞭然。偶数波はcos波の高調波から成る。対称波は奇数次の高調波のみから構成されるので、偶数波はかならず非対称波となる。 題意では第二高調波のみを含むということを暗にヒントとして与えているのである。 問題のひずみ波を基本波と第二高調波から成るとすると e=Em1*cos(ωt)+Em2*cos(2ωt) で表されることになる。 題意では正の最大値と負の最大値の絶対値がそれぞれ19と13ということになっている。 上のひずみ波の極大極小点を求めるために微分してみると e'=-ω*(Em1*sin(ωt)+2*Em2*sin(2ωt)) ということになる。極大点と極小点ではe'=0であることから Em1*sin(ωt)+2*Em2*sin(2ωt)=0 となるωtを求めて極大点と極小点について方程式を立てればよいことになる。 しかしどうすんだこれ。 偶関数のひずみ波の導関数はsin波のみからなる奇関数であることはわかる。 上の式の根には Em1*sin(ωt)=0かつ2*Em2*sin(2ωt)=0となる ωt=±nπ (n=0,∞) が含まれる。それ以外にも Em1*sin(ωt)=-2*Em2*sin(2ωt) となるtも含まれる。これは展開すると Em1*sin(ωt)=-2*Em2*(2*sin(ωt)*cos(ωt)) 従って Em1=-4*Em2*cos(ωt) ∴Em1+4*Em2*cos(ωt)=0 となるωtも極大極小値を取り得る。 すなわち cos(ωt)=-Em1/4*Em2 より ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) 最初の根を元のひずみ波の式に代入すると e=Em1*cos(±nπ)+Em2*cos(2*(±nπ)) =Em1*(-1)^n+Em2*cos(±2nπ) =Em1*(-1)^n+Em2 ということになる。この場合極大値と極小値はそれぞれ eMax=Em1+Em2 eMin=-Em1+Em2 ということになり、題意より eMax=Em1+Em2=19 eMin=-Em1+Em2=-13 と与えられているので、これをEm1とEm2に関する連立方程式として解くと (%i179) e1:Em1+Em2=19; (%o179) Em2+Em1=19 (%i185) e2:-Em1+Em2=-13; (%o185) Em2-Em1=-13 (%i186) solve([e1,e2],[Em1,Em2]); (%o186) [[Em1=16,Em2=3]] Em1=16 Em2=3 ということになる。確認のためにプロットしてみると wxplot2d([3*cos(2*x)+16*cos(x)], [x,-5,5])$ 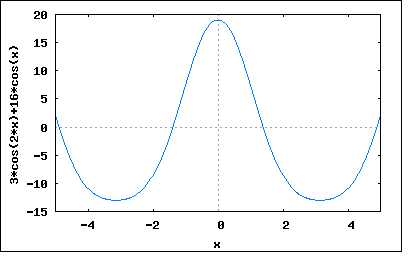 位相はずれているが確かに最大値と最小値の値はあっている。 一方もうひとつの根 ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) を代入すると e=Em1*cos(±acos(-Em1/4*Em2)±2nπ)+Em2*cos(2*(acos(-Em1/4*Em2)±2nπ)) =Em1*(-Em1/4*Em2)+Em2*cos(2*acos(-Em1/4*Em2)±2nπ) =(-Em1^2/4*Em2)+Em2*cos(2*acos(-Em1/4*Em2)) =(-Em1^2/4*Em2)+Em2*(2*cos(acos(-Em1/4*Em2))^2-1) =(-Em1^2/4*Em2)+Em2*(2*(-Em1/4*Em2)^2-1) =(-Em1^2/4*Em2)+Em1^2/8*Em2-Em2 =-Em1^2/8*Em2-Em2 ということになる。従って極大値と極小値は eMax=eMin=-Em1^2/8*Em2-Em2 どんな場合かはEm1=Em2=1と置いてプロットしてみると。 wxplot2d([cos(2*x)+cos(x)], [x,-5,5])$ 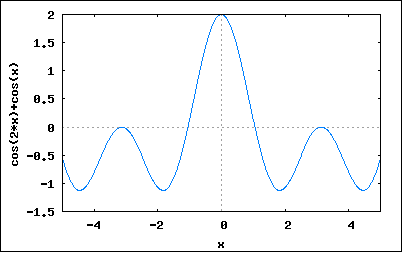 ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) =±acos(-1/4)±2nπ ωt=±1.8±2nπ のところに同じ大きさの極小点が存在することが確認できる。 そこで二つの根を組み合わせについても、もうひとつ解の存在が考えられる。 すなわち最初の根の極大値 eMax=Em1+Em2 ともうひとつの根の極小値 eMin=-Em1^2/8*Em2-Em2 で題意のeMax=19, eMin=-13を満足するEm1,Em2が存在するはずである。 解いてみると (%i229) e1:Em1+Em2=19; (%o229) Em2+Em1=19 (%i230) e2:-Em1^2/(8*Em2)-Em2=-13; (%o230) -Em2-Em1^2/(8*Em2)=-13 (%i231) solve([e1,e2],[Em1,Em2]); (%o231) [[Em1=-(16*sqrt(7)-100)/9,Em2=(16*sqrt(7)+71)/9],[Em1=(16*sqrt(7)+100)/9,Em2=-(16*sqrt(7)-71)/9]] Em1=(-16√7+100)/9, Em2=(16√7+71)/9 Em1=(16√7+100)/9, Em2=(-16√7+71)/9 という2つの組の解が得られる。実際にプロットしてみると wxplot2d([((16*sqrt(7)+71)*cos(2*x))/9+((100-16*sqrt(7))*cos(x))/9], [x,-5,5])$  中間のこぶがあるがが題意の最大値と最小値の条件は満足している。 もうひとつは別の極大値極小値の根から得たものとEm1,Em2の値は異なるが波形は同じである。 wxplot2d([((-16*sqrt(7)+71)*cos(2*x))/9+((100+16*sqrt(7))*cos(x))/9], [x,-5,5])$ 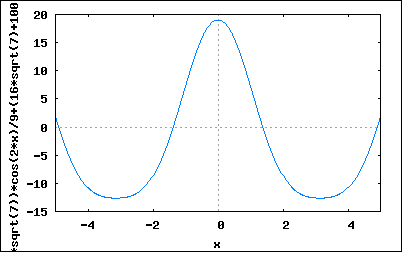 これらについて基本波と高調波の大きさの比を求めてみると最初の極大値極小値の根については Em2/Em1=3/16 =0.1875 であるのに対してもうひとつの極大値極小値の解については Em2/Em1=(-16√7+71)/(16√7+100) =0.201 Em2/Em1=(16√7+71)/(-16√7+100) =1.965 の3種類あるということになる。これが驚愕の事実である。 著者は、このもうひとつの極小極大値の根についての検討を怠って残りの2つの解の存在を見落としている。 P.S 実は組み合わせがもうひとつあって eMax=-Em1+Em2=19 eMin=-Em1^2/8*Em2-Em2=-13 これに関してEm1,Em2を解くと (%i263) e1:-Em1+Em2=19; (%o263) Em2-Em1=19 (%i264) e2:-Em1^2/(8*Em2)-Em2=-13; (%o264) -Em2-Em1^2/(8*Em2)=-13 (%i265) solve([e1,e2],[Em1,Em2]); (%o265) [[Em1=-(16*sqrt(7)+100)/9,Em2=-(16*sqrt(7)-71)/9],[Em1=(16*sqrt(7)-100)/9,Em2=(16*sqrt(7)+71)/9]] Em1=-(16√7+100)/9, Em2=-(16√7-71)/9 Em1=(16√7-100)/9, Em2=(16√7+71)/9 も解であることがわかる。確認のためにプロットしてみると。 wxplot2d([((-16*sqrt(7)-100)*cos(x))/9-((16*sqrt(7)-71)*cos(2*x))/9], [x,-5,5])$ 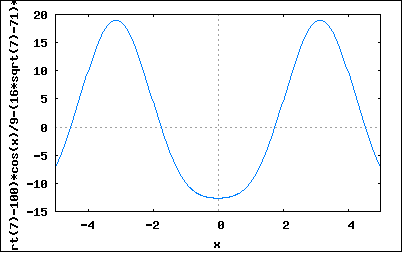 wxplot2d([((16*sqrt(7)-100)*cos(x))/9+((16*sqrt(7)+71)*cos(2*x))/9], [x,-5,5])$ 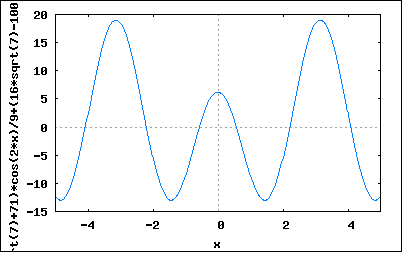 いずれも題意の最大値と最小値の条件を満足している、大発見である。 基本波と高調波の大きさの比を計算してみると Em2/Em1=(16√7-71)/(16√7+100) =-0.201 Em2/Em1=(16√7+71)/(16√7-100) =-1.965 と先の解と符号が反転しているため位相がずれて見える。 なぜ基本波と高調波の大きさが変わっただけで位相がずれて見えるのだろうか?それは読者の課題としよう(´∀` ) P.S 3 実は気になって波形を比べてみたところ、良く似ているが違っていることが発覚。 wxplot2d([3*cos(2*x)+16*cos(x),((-16*sqrt(7)+71)*cos(2*x))/9+((100+16*sqrt(7))*cos(x))/9], [x,-5,5])$ 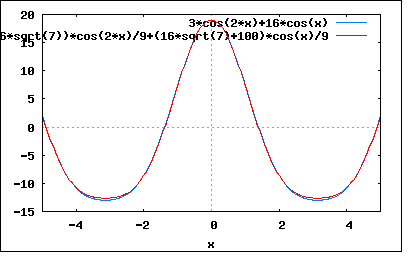 最小値が-13に若干足らない。確かにωt=πの時の値は-13にならないのである。なぜこのような解が出てきてしまったのかは謎。どこかにflawがあるのだろうか。たしかにこちらの解だと極大極小点の場所が違うので解としても怪しいのだが。しかし良く似ているのだから、少し値が違えばぴったり合う可能性もなきにしもあらず。 どうやら ωt=±acos(-Em1/4*Em2)±2nπ (n=0,∞) が成り立つのは |Em1/4*Em2| ≦ 1 の場合に限定されるような気がする。最初そう思ってこの条件をつけていたが、あまりにももう一つの解が波形がぴったり似ているので条件の記述を外してしまった。 実は問題に示されているのと同じグラフを描くために e=16*cos(ωt+π)+3*cos(2ωt) =-16*cos(ωt)+3*cos(2ωt) というのを知っていたので、これも実は解である。どちらかというと問題に示されている波形はこちらなのでこっちが正解かもしれない。 この場合 Em2/Em1=-3/16 =-0.1875 ということになる。 いずれにせよスペクトルが違えば同じ波形であるはずが無いというのは確認できた。 この妙なflawの解明は読者の研究課題としよう(´∀` ) |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

