Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 一端子対回路：演習問題

投稿者	スレッド
webadm	投稿日時: 2010-4-18 0:34
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3087	【15】続々：リアクタンス回路次ぎはリアクタンス回路の計算問題。以下の回路のリアクタンスとアドミッタンスを求めよというもの。回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large C_1 s+\frac{1}{\frac{1}{C_2 s}+L_1 s}+\frac{1}{L_2 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 L_2 s^2+1}{L_2 s}+\frac{C_2 s}{C_2 L_1 s^2+1}}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{\left(C_1 L_2 s^2+1\right)\left(C_2 L_1 s^2+1\right)+C_2 L_2 s^2}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{C_1 C_2 L_1 L_2 s^4+\left(C_1 L_2 +C_2 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{1}{C_1}\right)\frac{s\left(s^2+\frac{1}{C_2 L_1}\right)}{\left(s^4+\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}s^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{1}{C_1}\right)\frac{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)})\\<br />&=&\left(\frac{1}{C_1}\right)\frac{\omega\left(\frac{1}{C_2 L_1}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&\frac{\omega\left(25-\omega^2\right)}{\left(\omega^4-26.58\omega^2+8.33\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&C_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}\\&=&jC_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{\omega\left(\omega^2-\frac{1}{C_2 L_1}\right)}\\<br />&=&j\frac{\left(\omega^4-26.58\omega^2+8.33\right)}{\omega\left(\omega^2-25\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると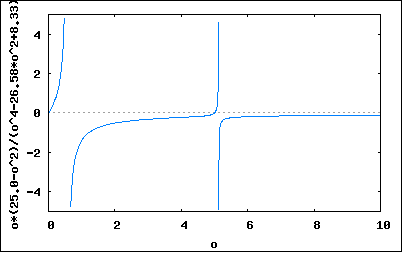アドミッタンスはちょうど零点と極が逆になった形になる。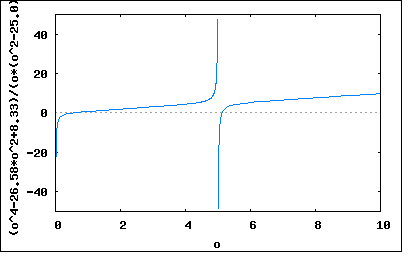回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large\frac{1}{\frac{1}{C_1 s}+L_1 s}+\frac{1}{\frac{1}{C_2 s}+L_2 s}+\frac{1}{L_3 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 s}{1+C_1 L_1 s^2}+\frac{C_2 s}{1+C_2 L_2 s^2}+\frac{1}{L_3 s}}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 L_3 s^2\left(1+C_2 L_2 s^2\right)+C_2 L_3 s^2\left(1+C_1 L_1 s^2\right)+\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)s^4+\left(C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{s\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{\left(s^4+\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}s^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)})\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{\omega\left(\frac{1}{C_1 L_1}-\omega^2\right)\left(\frac{1}{C_2 L_2}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\omega^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&0.11538\frac{\omega\left(66.667-\omega^2\right)\left(166.67-\omega^2\right)}{\left(\omega^4-153.85\omega^2+4273.5\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&\left(\frac{L_2 L_3+L_1 L_3+L_1 L_2}{L_1 L_2 L_3}\right)\frac{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}\\<br />&=&j8.6667\frac{\left(\omega^4-153.85\omega^2+4273.5\right)}{\omega\left(\omega^2-66.667\right)\left(166.67-\omega^2\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると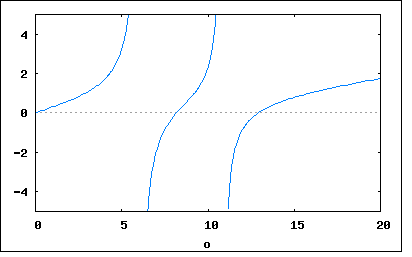アドミッタンスはちょうど零点と極が逆になった形になる。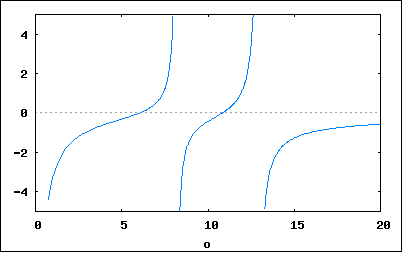

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
一端子対回路：演習問題	webadm	2009-12-28 23:05
【1】複素周波数の意味	webadm	2010-1-1 20:59
【2】インピーダンス関数	webadm	2010-1-8 11:16
【3】インピーダンス関数に対する一端子対回路	webadm	2010-1-8 11:24
【4】一端子対回路のインピーダンス関数	webadm	2010-1-8 21:05
【5】インピーダンス関数の零点及び極と留数	webadm	2010-1-9 20:37
【6】正実関数、インピーダンス関数、アドミッタンス関数	webadm	2010-1-10 20:46
【７】正実関数	webadm	2010-3-30 9:20
【8】続：正実関数	webadm	2010-4-11 1:24
【9】続々：正実関数	webadm	2010-4-13 10:40
【10】インピーダンス関数とその回路	webadm	2010-4-15 9:49
【11】リアクタンス回路	webadm	2010-4-15 17:02
【12】続：リアクタンス回路	webadm	2010-4-15 19:39
【13】リアクタンス関数	webadm	2010-4-17 22:57
【14】相互インダクタンスを含むリアクタンス回路	webadm	2010-4-17 23:35
» 【15】続々：リアクタンス回路	webadm	2010-4-18 0:34
【16】リアクタンス回路の合成	webadm	2010-4-19 2:30
【17】続：リアクタンス回路の合成	webadm	2010-4-19 10:09
【18】続々：リアクタンス回路の合成	webadm	2010-4-20 4:22
【19】またまた：リアクタンス回路	webadm	2010-4-20 9:55
【20】インピーダンス関数	webadm	2010-4-21 23:11
【21】続：インピーダンス関数	webadm	2010-4-22 12:29
【22】続々：インピーダンス関数	webadm	2010-4-24 4:03
【23】またまた：インピーダンス関数	webadm	2010-4-24 11:55
【24】アドミッタンス関数	webadm	2010-4-24 20:47
【25】続：アドミッタンス関数	webadm	2010-4-27 10:19
【26】密結合変成器の分離	webadm	2010-4-28 9:20
【27】逆回路	webadm	2010-4-29 19:35
【28】続：逆回路	webadm	2010-4-30 9:49
【29】続々：逆回路	webadm	2010-4-30 10:15
【30】まだまだ：逆回路	webadm	2010-4-30 10:59
【31】もうひとつの：逆回路	webadm	2010-4-30 12:03
【32】定抵抗回路	webadm	2010-5-1 9:55
【33】続：定抵抗回路	webadm	2010-5-2 16:00

投稿するにはまず登録を