| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-5-4 9:24 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3089 |
概説 著者は手短に天下り的に古典的フィルターの分類を説明しているが、それ以前に漠然とした疑問が邪魔をしてそのまま読み進めるわけにはいかない。
その疑問とは誰が最初に最初のフィルターを考案したのかという点。それには必然性があったのだろうかという点。 交流回路理論を学んだ際にRC直列、RL直列回路の素子の分圧周波数特性を見ると低域通過特性や広域通過特性を示すことが確かめられた。 おさらいのために以下の2つの回路について周波数ゲイン特性を導いてみよう。 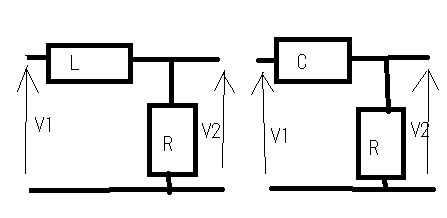 左の回路について以下の関係が成り立つ H=R/L=1とおいて周波数ゲイン特性を対数グラフにプロットすると 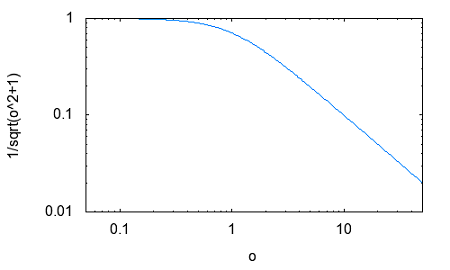 より低域ほど通過し高域になるほど減衰させる低域通過フィルタのように見える。なんとか対数グラフにしてそれらしく見えるけど、どこからどこまでが通過帯域なのか減衰帯域なのか判別がつかない。カーブが極めて緩やかである。 右側の回路についても同様に H=C*R=1と置いて周波数ゲイン特性をプロットすると 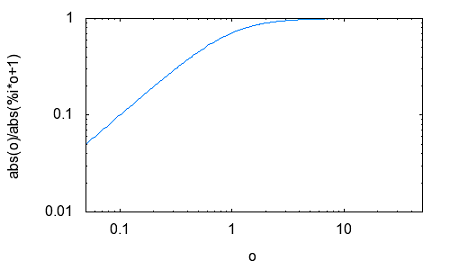 ということで高域通過フィルタのように見えるが、やはり通過域と減衰域の境界が不鮮明であることは否めない。 この2つの従属接続するとかLとCの定数をうまく選定することで特定の帯域を通過させる帯域通過フィルタや特定の帯域を減衰させる帯域除去フィルタとかができないだろうか? おそらく原始フィルタ理論はこのようなところから出発したのかもしれない。 上の2つの回路には以下の不満がある (1)もっと周波数減衰特性が急峻で通過帯域では平坦にできないか? (2)自由に通過域と減衰域の境界周波数を設定できないか? (3)多の回路を従属接続しても特性に影響を与えないようにできないか? (1)は似たような緩やかな特性のフィルタを複数従属接続して減衰特性を強調すると同時に通過領域を平坦にできないか? (2)はLとCを併用することで共振点や逆共振点(零点と極)をうまく使えないか? (3)は(1)と(2)にも共通し二端子対回路で学んだ映像パラメータ(線形代数の線形変換の固有値と固有ベクトル)が使えないか? そういう感じでフィルタ理論の発展を追体験していくことにしよう。 自宅に戻って古典フィルタ理論について触れている参考書を探してみたところ、以下の3つがあった。 「大学教程 電気回路(1)(第3版)」大野克朗、西哲生 共著 オーム社 「Network Analysis」by M.E.VAN VALKENBURG PRENTICE-HALL, INC. 「Einfuhüfrung in die theoretische Elektrotechnik」 Von K.Küpfmüller Seehste Auflage 最初のは現在でも増刷されているはず。都内の大型書店で購入したもの。残りはオークションで手にいれた貴重な古本。最後のはドイツの理論電気学の教科書。電気回路理論と電磁気学が織り合わさるように学んでいくドイツ流。 アインシュタインは学生時代にこの科目だけはダントツで成績優秀だったらしい、それだけに電磁気学に精通もしていたし何がそこに欠落しているか見通していたのかもしれない。 1冊目はすでに古典的な価値しかないが先人の知恵を紹介するという形で二端子対回路理論の反復パラメータや伝達パラメータを解説し、その上で古典フィルタを説明している。 日本での用語が戦前はドイツから戦後は欧米から取り入れたものが混在しているのでその点も理由を説明してくれている。ドイツの本を手にいれていてよかった。 2番目の本は戦後に書かれたもので、古典フィルタ理論の章は一端子対回路(ONE-TERMINAL-PAIR REACTIVE NETWORKS)の次の章で「TWO-TERMINAL-PAIR REACTIVE NETWORKS(FILTERS)」という名前になっていることから、元々は二端子対回路がフィルタ理論そのものであったと考えられる。 Valkenburgは歴史的なエピソードを添えることが多いので単純な疑問に答えてくれる。 3番目の本を読むと、フィルタは日本で出版されている本と違って、二端子対回路と分布定数回路の後に登場する。このことから、歴史的にこれらの理論が研究されたのが電話が発明され普及し始めた黎明期であることが想像に難くない。 電話網を分布定数回路である回線と交換機内の各種伝送回路をそれぞれ二端子対回路とするとその縦続接続とみなす方法この頃に発案されたようだ。 確かに当初の電話網はすべてアナログ方式であり、増幅や歪み補正や多重化の際に優れた所望の特性をもつフィルタが必要になることは明らかである。 電子回路ハンドブックなどを見ると詳しい解説は無いが実用的なアナログフィルタの設計公式が載っている。しかしそれを使うにはやはり理論を多少なりともかじっていないと無理だろうと思われる。 今日的にフィルタ理論というと、古典的な受動素子だけのフィルタではなく、その中心はオペアンプを使ったアクティブフィルタであったり、デジタルフィルタに移ってきている。もちろん高周波やマイクロ波の世界では未だに受動素子だけのフィルタが必要とされる。 さて最初の目標である (1)もっと周波数減衰特性が急峻で通過帯域では平坦にできないか? というのは当時難問であったと想像される。おそらく思考錯誤で受動素子を組み合わせた回路をひとつひとつ解析するのでは解決しそうもない。もっともそういった試行錯誤からなんらかのヒントが得られる可能性はあるが。 おそらく急峻な特性を要求されるのは複数の電話音声を多重化して伝送する際にクロストークを押さえるための低域通過フィルターが最初だったと想像される。 音声を伝送するために必要な周波数帯域は狭くてもよいので、当時開発されたSSB変調方式で複数の周波数チャネルに詰め詰めでたくさんの異なる音声を乗せて遠距離ケーブルで伝送し、復調する際に各チャネル毎に1つの音声帯域だけ通過させ隣接するチャネルの信号は取り除く。 すぐ隣の帯域には別の音声チャネルがあるので、フィルタが急峻でないとそちらの信号が混じってクロストークが発生する。 現代では電話網は末端を除いてはすべてデジタル化されているのでそれらは使われなくなったが、それ以前までははそれが主流だった。 今時SSB変調を使っているのはアマチュア無線と船舶無線ぐらいだろう。デジタル変調が情報伝送の主流になってしまった今ではしかたがないことだ。 さて受動素子だけからなる二端子対回路を複数縦続接続してフィルタを構成するとなると、増幅回路ではないのでゲインよりもロスを評価するほうがよい。これは以前に学んだ二端子対回路の伝達係数や伝搬係数と同じである。 電話の時代にも最終的には人間の耳が終端になるので、人間の感覚は信号振幅の対数に比例する(Weber-Fechnerの法則)のと見合って都合がよい。 これらは伝送量と呼ばれドイツ語のŨbertragungmaßの日本語訳らしい。Ũbertragungが伝送、maß(mass)が量というわけだ。元々は分布定数回路の伝搬定数である。 先のLR回路の定常状態での電圧伝送量は ということになる。γのことを伝送量と呼ぶ。伝達関数を対数変換したものである。 αは減衰量(Dümpfungsmaß,attenation)でωが大きくなるにつれ大きくなることがわかる。βは位相量(Phasenmaß, phase shift)である。前者の単位はネーパー(Np,neper)で後者はラジアン(rad,radian)である。 同じ頃に米国Bell研究所では常用対数で減衰量を表すベル(B)とその10分の1のデシベル(dB)いう単位を提案している。 デシベルは常用対数なので対数変換する前との関係がわかりやすい利点がある。先の電圧比の伝送量とデシベルとの関係は という関係がある。自然対数と常用対数は必ず試験にでるので忘れないようにしよう。といってもすぐ忘れる(;´Д`) 著者はこの次にいきなり定Kフィルタを登場させている。先に挙げた参考書では二端子対回路の映像パラメータが登場する。すでに学んでしまったのだが本当はフィルタ理論の初歩で学ぶべきことだったのだ。 ここまで来ると先の2つの回路の周波数ゲイン特性の意味がようやく見えて来る。よく見ると2つの直線の合成になっていることに気づく。H=1として減衰量を対数グラフでプロットすると上の式からも明らかである。 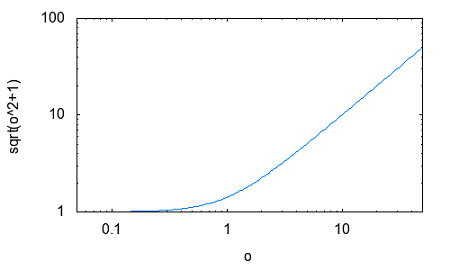 従って傾きを急峻にするには同じような回路を複数縦続接続すれば減衰量は足し算で効いてくるので傾きも上向くはずであるということも予想がつく。 傾きが変化する点はどうやら1/H^2によって決まるらしいことがわかる。Hを下げればグラフは右にシフトしそうである。H=0.1としてプロットし直すと 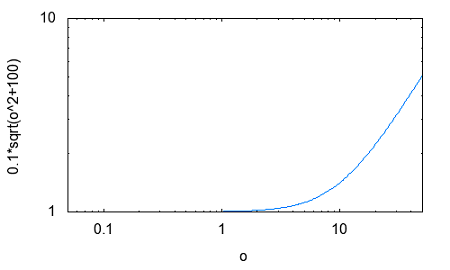 おお、確かに右にシフトした。しかし傾きも影響を受けているぽい。これはフィルタ理論で言うところの周波数変換である。 この回路のRの代わりにCを使うLC直列回路なら高域でさらに減衰量を増やすことができるとすぐに思いつく。しかし難点もあるLC直列回路には共振点が伴う。零点が存在することになる。しかし現実の回路では必ず回路に損失(抵抗)を伴うのでひとつ研究してみる価値はある。 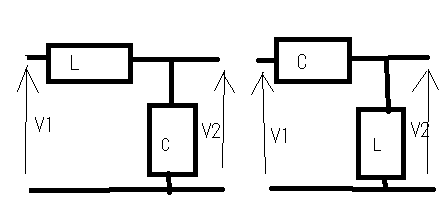 左の回路の伝送量を導くと H=1として減衰量を対数グラフにプロットすると 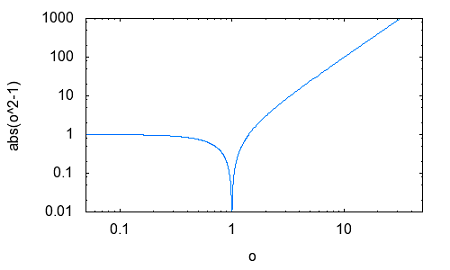 これも低域通過フィルタの特性を有している。零点の部分は減衰ではなくゲインが大きくなることを意味している。 今日対数グラフのプロットは計算機で簡単にできるけど、計算機も電卓もなかった昔の人は式と対数表を使って一つ一つプロットしていったと思われる。 グラフを描かずとも式を見ればだいたいの傾向が見通せるようでなければならない。対数に変換することでそれも容易くなるのは先人の知恵である。 他にもいろいろそうした知恵が残されているが計算が楽になった現代では有り難みが薄いと軽んじてしまう傾向がある。 もうひとつ古典フィルタ理論に触れている電気回路の本が自宅にあるのを発見した。 「電気回路」木戸正夫、山田嘉夫 共著 朝倉書店 割と薄い本だが電気回路の要点をすべてカバーしている。フィルタは4端子回路の章で「分布定数回路の4端子回路網としての取り扱い」という節の後に登場するドイツ流である。 分布定数回路は4端子回路として扱う場合だけを説明し、フィルタ理論につなげている。多くの電気回路の本は分布定数回路はずっと後にどっさりと教えるという重い扱いをしているので対照的だ。 電気回路の初歩という意味では4端子回路として見るだけでも十分難易度が高いのではないかと思える。 ここで動作減衰量(Betriebsdämpfung)というのが先のドイツの本や「電気回路(1)」で登場する。二端子対回路がLCだけから成る場合、回路の中では電力は消費されず、出力端に接続された負荷の抵抗成分によって消費され、入力端からはその電力だけが供給される形になる。 定K形フィルタや誘導M形フィルタでは映像パラメータが用いられていたが、その後登場した最初からLCラダー回路として合成されることを前提としたButterworth(Wagner)特性やTchebycheff(Chebyshev)特性のフィルタ評価には動作減衰量が用いられるようになったためである。 従ってそれらの近代的な(すでに古典であるが)フィルタを扱わない本では動作減衰量も登場しないということになる。 著者は概説で上記のことを触れるだけで、映像インピーダンスで終端することを前提とした古典フィルタの定K形と誘導M形を解説するにとどまっているため、動作減衰量そのものは必要なく割愛されている。 「電気回路(1)」では逆に定K形や誘導M形を割愛し、より近代的なButterworthとTchebycheffだけに絞っている。そのため動作減衰量の解説が登場する。残念ながらこれが紙面の都合上か結論だけで実にわかりにくい。後のフィルタ特性評価式とのつながりがわからない。 検索してももはや古典的すぎて用語の定義以外はそれが使用された文書や論文しか見当たらない。なおさら理解してやろうという思いが募るのは天の邪鬼な性格のなせる技かもしれない。 結局原理的な解説を載せているのは先に紹介したドイツの理論電気学の教科書である。たぶん今も同じ題名の本の改訂版が増刷されていると思われるが内容が昔とは変わっているかもしれない。 以下の回路で考えてみよう。 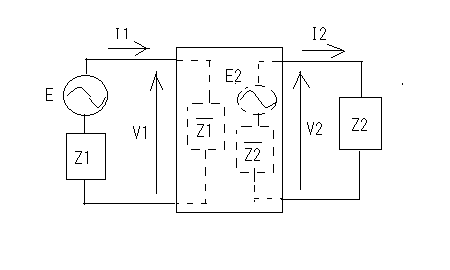 供給される電力が最大となるのは、負荷インピーダンスが電源の出力インピーダンスと複素共役となる場合であるのは供給電力最大の法則から自明である。実を言うとすっかり忘れていたのは内緒だ。その条件で以下の関係が成り立つ。 どうすんだこれ(;´Д`) ドイツ語(Betriebsdämpfung)で検索したら本家だけあって書籍やら講義資料とかたくさんある。でも書いてある人や目的によって導き方が違うのがなんともわかりずらい。 どうやらドイツ語のNachrichtentechnikというのと関係するみたいだけど、日本語訳だと通信工学だけど、ちょっと日本で教えられている通信工学とドイツのそれが同じとは限らない。 一応ドイツ語の教科書もしっかりしたのがあるようだ。ドイツの本を見るとどれも内容が半端じゃない。どの工学の本も一冊あればそれを学ぶのに必要なことは全部書いてあるという感じ。でもわかんねー(;´Д`) ちょっとわかったことだけ書くと、入力端から供給可能な最大電力は供給電力最大の法則から ということになる。一方で出力端の負荷に供給される電力は 従って動作減衰量は ということになる。とりあえず出力側は等価電圧源とかは考えなくてもよいらしい。 更に二端子対回路が対称回路の場合には入力と出力のインピーダンスは等しくなるのでZ_1=Z_2と置くと ということになる。位相遷移も含む複素数の動作伝送量を定義すると ということになる。 本家ドイツの本には自然対数での定義が説明されていて混乱を招く。 という感じ。さてこれで動作量の話は終わりにしよう。 ここまでを最初から携帯のiモードで読み返していたら最初の方でだいぶ式の操作を間違っていたことが発覚(;´Д`) 複素数の絶対値の取り方をすっかり間違えているし。グラフも全部プロットし直した。それとパラグラフが長すぎる。こっそり修正。 人のことは言えないが検索すると減衰量に関して明らかに違和感のある誤用が目立つ。「減衰量は-60dbあります」とかである。減衰量は0以上の正の値をとるはずだが(減衰するのだから入力よりも出力は小さくなるはず)、小さいという意識がマイナス値を違和感なく誤用してしまう。電子部品の商社でさえも当社測定値として伝送回路部品の減衰量に負の値を示している。おそらく測定にゲインフェーズアナライザを使用したのだろう、ゲインで測定すれば減衰は負の値になる。ゲインと減衰量を誤用しているだけであるとすぐ気がつくが、ぱっと見違和感がある。アマチュアのオーディオアンプ制作者の記事とかにも同じ誤用が見られる。 LC回路で作るフィルタに話しを戻そう。共振点である零点は素子の定数を設定することで任意の周波数にできるのでフィルターの基本回路としては有用であることは明らかである。RLやRC回路のように素子定数を変えると傾きの鋭さも影響を受けてしまうということも無い。 右の回路の様にLとCを逆にすると高域を通過させるようになることが想像できる。ちょっとやってみよう。 H=L*C=1と置いて減衰量をプロットすると 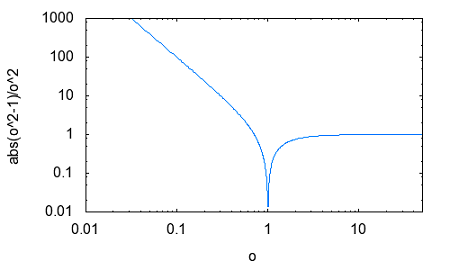 といい感じである。 右の回路と左の回路を縦続接続して互いの零点を異なる周波数に移動させれば特定の周波数領域を通過させたり、阻止したりするフィルターが組めそうである。 これによってLC回路で以下の4種類のフィルターが実現できることになる。 (1)低域フィルタ(low pass filter: LPF) (2)高域フィルタ(hight pass filter: HPF) (3)帯域フィルタ(band pass filter: BPF) (4)帯域除去フィルタ(band elimination filter: BEF) (1)と(2)はすでに示した通り。 (3)の帯域フィルタを実現するには、通過帯域の上限周波数にLPFの零点を、下限周波数にHPFの零点を設定して縦続接続すればいけそうな気がする。 LPFとHPFを縦続接続した以下の回路の減衰量を導く 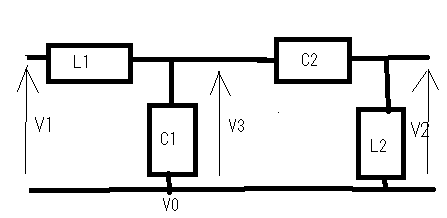 どーすんだこれ(;´Д`) とりあえず厳密な解析は後回しで、先に導いた左の回路と右の回路のそれぞれの伝送量の式から全体の伝送量をざっくり合成してみよう。 H1=C1*L1=0.1,H2=C2*L2=1と置いて対数グラフにプロットしてみると 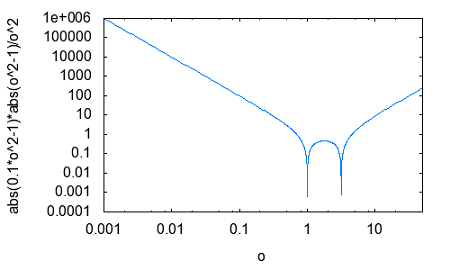 いい感じで零点が帯域通過領域の上下限と密接な関係があることがわかる。 (2011/5/13 H1とH2の関係が逆だったので通過領域に大きなロスが生じてしまっていたのを訂正) ただしこれは厳密には上の回路の特性ではない。単に意図した場所に零点を持つ伝達関数の周波数特性をプロットしただけである。 キルヒホッフの電流則から以下の関係が成り立つ (2011/05/17 立式が間違っていたので訂正(;´Д`)伝送行列をから求めたのと違っているので手計算の間違いが発覚、伝送行列から求めた方が簡単かも) 分母を払って整理すると 第二の式からV3を求めて第一の式に代入してV2について解くと 従って伝送量は ということになる。ここでさっきと同様にH1=C1*L1=0.1,H2=C2*L2=1、ただしC1=L1=1/√10,C2=L2=1と置いてプロットしてみると(2011/5/13 H1とH2の大小関係が逆だったのを訂正) 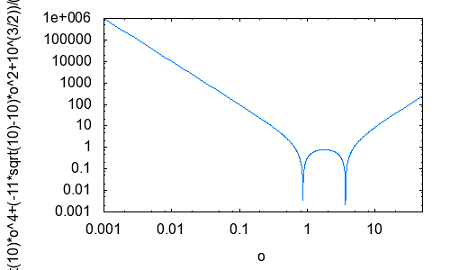 おお、ちょっと零点の位置がシフトしているけどちゃんと帯域通過フィルタになっている。 当初手計算でやって導いた式が間違っていて思わぬ方向へ進んでしまったが、後で伝送行列を求めてその開放電圧伝達比(A)の式をみたら違っていたので誤りに気づいた次第。 さてそれでは2つのグラフに微妙な差異が出るのはなぜだろう? 伝送行列を計算してみて明らかなのは異なる二端子対回路を縦続接続した場合には合成された回路の開放電圧伝達比は元の部分回路の開放電圧伝達比の積とは異なるのが原因である。 これが古典的フィルタ回路設計の悩ましいところである。ラダー回路は段数を重ねるととたんに多項式の次数が高くなり零点や極を求めるのが困難になる。従って計算機の無い時代には手計算で解析可能な単純な回路で構成されたフィルタを縦続接続するcomposite filterが最初に登場したのは頷ける。 それでは縦続接続した際にそれぞれの部分回路の零点や極が変わらないようにするにはどうすればいいのだろう。 一つの答えは開放電圧伝達比ではなく映像インピーダンスと映像伝達定数を用いるというアイデアである。そうすれば映像インピーダンスがマッチングしている限り、縦続接続された回路の映像伝達定数は部分回路の映像伝達定数の単純な足し算になる。映像インピーダンスは伝送行列の固有値(映像伝達定数)に対する固有ベクトルの成分であるため比較的求め易い。 映像インピーダンスや伝達定数を新たな視点で見直すために以下の図を考える。Z11,Z22はそれぞれ映像インピーダンスである。Z11を接続した状態で出力端子端子対の駆動点インピーダンスはZ22、逆にZ22を出力端に接続した状態で入力端を開放した際の入力端の駆動点インピーダンスがZ11となる。 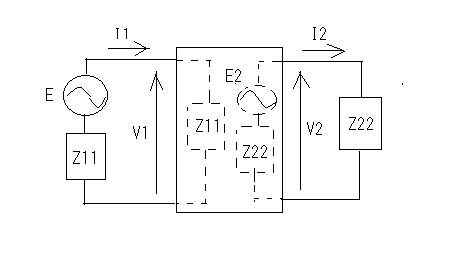 視点を変えれば、出力端の映像インピーダンスZ22はZ22を負荷として接続した場合に負荷への供給電力が最大となる出力インピーダンスということになる。さてこの場合、等価電圧源E2は入力側の電圧源Eとどんな関係にあるのだろうか? 伝達定数の定義から ということでI1,I2やV1,V2と同じ関係になるということだった。これは演習問題としては引っかけ問題でよいかもしれない。 上の式を別の観点から見ると、Z11=Z22となる対称回路ではE/E2=I1/I2=V1/V2=e^θという単純で分かりやすい関係になる。 VALKENBURGのNETWORK ANALYSISでは定K形フィルタを登場させるまでに映像インピーダンスやLCリアクタンス回路の性質など今日ではめったに見かけない退屈とも思える議論をしている。おそらく古典フィルタ理論が誕生した時代の試行錯誤的な歴史的な過程を忠実にたどっているのかもしれない。 ひとつ興味深い記述をここに紹介しよう。これまでやったようにラダー形回路は素子数がちょっと増えただけですぐに高次の多項式となり計算で零点や極を割り出すのが困難になってくる。計算機がなかった昔には実際に以下の様な実験回路を組んで、テストオシレータとオシロスコープを使って見いだしたというのである。 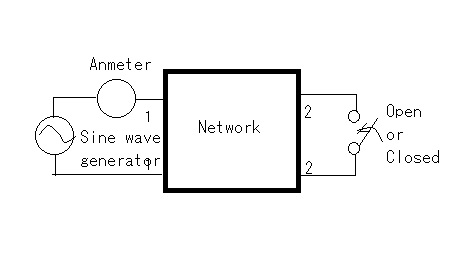 二端子対回路ですでに学んだ通り、対称回路では入力側から見た開放駆動点インピーダンスと短絡駆動点インピーダンスがわかれば映像伝達関数もわかるというのである。これは未知のフィルタ回路の伝達定数を評価するの手っ取り早い方法である。実験テーマとしても面白いかもしれない。 図のAnmeterは交流電流計だが、抵抗値の小さい電圧降下用抵抗とオシロスコープの組み合わせでもよい。Sine wave generatorは低周波オシレータを一定の出力レベルを保つように周波数をスイープしていけばよい。これはネットワークアナライザの原型である。 対称回路ではないが先の帯域通過フィルタ回路でこの実験を行った場合を計算でシミュレーションしてみよう。後日時間があったら別途実験をしてみたい。 入力から見たそれぞれの駆動点インピーダンスを求めると 従って2つの駆動点電流Isc,Iocを導くと C1=L1=1/sqrt(10),C2=L2=1としてそれぞれをプロットして並べると 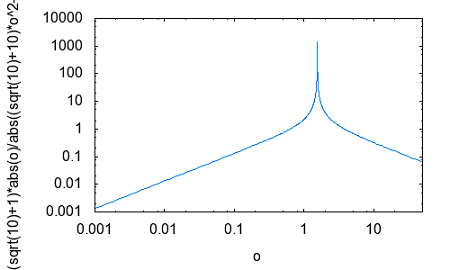 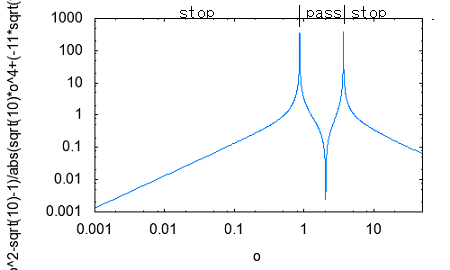 |Isc|,|Ioc|はそれぞれの駆動点インピーダンスの零点で最大値をとり極で最小値をとる。実際の回路ではLCのみからなるリアクタンス回路でも抵抗分があるため電流はゼロや∞にはならない有限の値の範囲をとる。Iscが最大値をとり、Iocが最小値をとるもしくはその逆の場合は通過領域である。Iscが最大値か最小値をとる時にIocがそうでない場合、もしくはその逆の場合そこが遮断周波数(cutoff frequency)である。Iscが最大値でIocが最小値またはその逆の場合には阻止領域である。ということらしい。 上のグラフだと真ん中は微妙にIscの最大値とIocの最小値が隣接しているので微妙なところだけど実際には相殺しあって通過領域ということになる。この回路は帯域通過フィルタなので通過領域の両サイドに阻止領域があるのが見てとれる。一方のカーブの傾きが他方と同じ領域は阻止領域で逆なのは通過領域とも見てとれる。確かに以前にプロットした電圧伝達比のカーブと比べてみると、これだけで遮断周波数とかがわかるんだと昔の人の知恵に驚かされる。こういうのは意外と大事かもしれない。 昔の人はこうやって知恵を絞りながらフィルタの研究をしていたのかと感嘆させられる。 この簡単なネットワークアナライザは能動素子を含む回路には使えない。受動素子のみから成る回路の場合だけ2つの駆動点インピーダンスから伝達定数が予想できる。 さて残った(4)帯域除去フィルタはどうやったら実現できるだろうか? 単純に考えてもLPFとHPFの縦続接続では実現できない。前段の遮断周波数より低域もしくは高域どちらか一方が先に遮断されてしまうので、後段で遮断された領域を通過させてもLPF/HPF/BPFにはなってもBEFにはならない。 縦続がだめなら並列にするしかない。そうすればLPFとHPFの双方の通過帯域の倫理和が全体の通過帯域になり、双方の遮断領域の論理積が全体の遮断領域になるという寸法だ。 さてそれを回路にするとどうなるのか考えてみよう、二通り思いつくが本当に期待通りにBEFとして機能するかは計算してみないとわからない。回路シミュレーターが手元にあればもっと簡単に確かめることができるのだが。そうだ先ほどの簡易ネットワークアナライザー技法を使って簡単に予想をつけるという手もある。 著者は具体的にBEFの回路を後に示しているのでここでは割愛しよう。 ところで自宅にもう一冊フィルタ理論を扱った本が買ってあったのを発見。ブックカバーがかけてあったのと専門的な内容に絞った本だったので今まで開く機会が少なかったのだった。 「線形回路理論」高木茂孝著 昭晃堂 まえがきを読んだらフィルタ理論の入門書ということだった。読み直して見ると確かによくまとまっている。なるほどフィルタ理論に絞り込むとかくもすっきりと道筋が整理できるのか。 電気回路一般を扱う本では出てこないもうひとつのフィルタのタイプがこの本には挙げられている。以前に二端子対回路の最後に出てきた、全域通過型である。その後の解説も回路設計の観点から説いているので技術者にはしっくりする。そのため一般の電気回路の本とはだいぶ異なる様相になっている。これはこれで技術の再構成とも言えるかもしれない。 今までとっつき易い開放電圧伝達比に着目してきたが、上記の本ではこれをR-∞型構成としてLC回路フィルタの構成として最初に説明している。出力端を開放すると入力から見た駆動点インピーダンスを連分数展開(Cauer展開)すれば回路が構成できる。分かりやすい。その他、0-R型構成とR-R型構成を例にあげ、最後のものが特性的に優れて実用的であることが示されている。上記の本はそこで終わっているの入門書とまえがきにある所以だ。 それと伝達関数、伝送量等の用語に関する日本語的な紛らわしさもいくつかの参考書で指摘されている。利得(ゲイン)に着目するのと損失(ロス)に着目するのとでは定義が互いに逆数となる。英米では挿入損失(insertion loss)という用語があったらしいが、現代では使われなくなったらしい。あらかじめ伝送量が入力と出力の比率の対数であることを知っていればそう大きな間違いはないが、それを知らないとまったくの誤解を生むことになる。 更に一歩深入りすれば、利得が得られる理由や損失が生じる理屈を知りたいということになる。結果的に入力された電力の一部だけが出力側に出ていき残りは入力に反射して戻ると考えると納得がいく。そうした観点からSパラメータなるものが有用になるが、電気回路理論ではそこまでは必要とされないので割愛されている。高周波回路やマイクロ波回路では必須なのでそこで学べばいいということだろう。 とりあえずフィルタ回路ではインピーダンスの整合が性能に重要な影響を与えることだけは頭にとめておくことことにしよう。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-5-3 7:21 |
| » |
webadm | 2011-5-4 9:24 |
| |
webadm | 2011-5-24 5:11 |
| |
webadm | 2011-6-1 5:49 |
| |
webadm | 2011-6-10 5:50 |
| |
webadm | 2011-7-18 1:22 |
| 投稿するにはまず登録を | |

