ログイン
ユーザ名:

パスワード:


パスワード紛失

新規登録
Main Menu
Tweet
Facebook
Line
:-?
フラット表示 前のトピック | 次のトピック
投稿者 スレッド
webadm
投稿日時: 2011-6-1 5:49
Webmaster
登録日: 2004-11-7
居住地:
投稿: 3089
誘導M形フィルタ
定K型フィルタに引き続き誘導M形フィルタを学ぶことにしよう。

誘導M形フィルタで検索すると、"誘導M形","誘導m形","誘導m型"といろいろ出てくる。英語では"m-derived filter"や"M"-drived filterとか見受けられる。web辞書とかでは"derived m-type filter"とまるで和製英語みたいなものも見受けられる。

どれが本当なんだ（；´Д｀）

欧米ではm-derivedもしくはm-type filterしか用いられていない。

おそらくderived m-type filterは誘導m型フィルタを英訳した和製英語だろう。m-derived filterで検索すると、m-derivedが英文の先頭に現れる場合だけM-derivedと大文字になっていることから、本当は小文字のmで、英文表記のお約束から文の先頭（主語）になるときだけ大文字のMとなると思われる。なのでそうでないケースでは小文字のmが正しいのだ。そうすると誘導M形という日本語訳も正確ではなく、本来は"誘導m形"とすべきだろう。誰だよ最初に訳したのは、出てこい。

それはどうでもよくて、問題なのは"derived"が"誘導"と訳されている理由だ。誘導Mというとまるで相互誘導インダクタンスのMを彷彿とさせる。これは明らかに誤訳だろう。元々はfに対するf'で記述されるderived function(導関数）とかのように元の形から一定の操作で導出されたものという意味だと思われる。m導出フィルタと直訳したほうがいいかもしれない。まあ導という字があるから許して置こう。

Valkenburgはその著書Network Analysisで定K形フィルタに続いてZobelがいかにして誘導M形フィルタを導き出したかその思考過程を述べている。おそらく信じるにたるものと思われるので、ここに紹介しよう。ほとんどの電気回路理論の本では結論だけを紹介しているのみでそれに至る過程は教えてくれない。

英語版のWikipediaにもそれらしき解説はあるが分かりやすいとは言えない。そもそも書いた本人が理解しているのかもあやしい。

定K形フィルタの欠点はZ1Z2が定数となるように制約を受ける点である。Zobelは定K形フィルタと同様に複数の対称T字回路や対称π形回路を縦続接続してラダー形フィルターを構成する複合フィルタ(composite filter)設計技法を前提に、各部分回路が同一の映像インピーダンスを持ち整合がとれ、かつ遮断周波数付近の減衰域で定K形フィルタよりも大きな減衰定数をとる回路ができないか思案した。

すなわち以下の図様に同じ映像インピーダンスを持ちながら目的の仕様（遮断周波数付近の減衰定数が定Kフィルタよりも大きい）Z1',Z2'というZ1,Z2から導出されたシリーズインピーダンスとシャントインピーダンスが存在すると仮定する。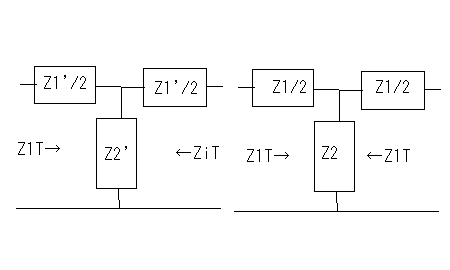



Zobelは次にZ1'がZ1から次なる関係で導かれると仮定した。

\begin{eqnarray}<br />Z_{1}^{\'}&=&m Z_1<br />\end{eqnarray}

ここでmは定数である。ちょっとこの仮定は唐突な感じが否めない。本来は減衰特性を遮断周波数付近で急峻にする目的とどうつながるのかはこの時点では予想もつかない。

二つの対称T字回路は同一の映像インピーダンスを持つことから

\begin{eqnarray}<br />Z_{iT}&=&\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}=\sqrt{\frac{{Z_{1}^{\'}}^2}{4}+Z_{1}^{\'}Z_{2}^{\'}}\\<br />{Z_{iT}}^2&=&\frac{{Z_1}^2}{4}+Z_1 Z_2=\frac{{Z_{1}^{\'}}^2}{4}+Z_{1}^{\'}Z_{2}^{\'}<br />\end{eqnarray}

という関係が成り立つ。これにZ1'の関係式を代入してZ2'について解くと

\begin{eqnarray}<br />Z_{2}^{\'}&=&\frac{1}{Z_{1}^{\'}}\left(\frac{{Z_1}^2}{4}+Z_1 Z_2-\frac{{Z_{1}^{\'}}^2}{4}\right)\\<br />&=&\frac{{Z_1}^2}{4Z_{1}^{\'}}+\frac{Z_1 Z_2}{Z_{1}^{\'}}-\frac{{Z_{1}^{\'}}}{4}\\<br />&=&\frac{{Z_1}\cancel{^2}}{4 m \cancel{Z_{1}}}+\frac{\cancel{Z_1} Z_2}{m \cancel{Z_{1}}}-\frac{m{Z_{1}}}{4}\\<br />&=&\left(\frac{1-m^2}{4 m}\right)Z_1+\frac{1}{m}Z_2<br />\end{eqnarray}

ということになる。

この式を回路に反映すると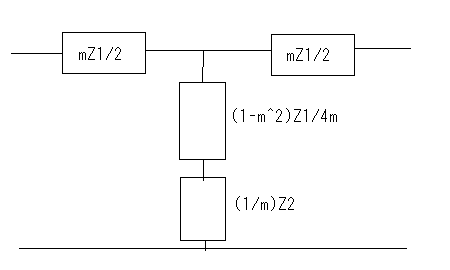



ということになる。

大抵の電気回路理論の本では、この対称T字回路の半回路(half section)である非対称逆L字回路を誘導m形フィルタとして説明している。

対称π形回路についても同様のアプローチで

\begin{eqnarray}<br />Z_{2}^{\'}&=&\frac{Z_2}{m}<br />\end{eqnarray}

とし。定K形フィルタの対称π形回路のZ1,Z2から導出したZ1',Z2'で構成される新しい対称π形フィルタとでは映像インピーダンスが等しいとすると

\begin{eqnarray}<br />Z_{i\pi}&=&\frac{Z_1 Z_2}{\sqrt{\frac{{Z_1}^2}{4}+Z_1 Z_2}}=\frac{Z_{1}^{\'}Z_{2}^{\'}}{\sqrt{\frac{{Z_{1}}^2}{4}+Z_{1}^{\'}Z_{2}^{\'}}}\\<br />{Z_{i\pi}}^2&=&\frac{{Z_1}^2{Z_2}^2}{\frac{{Z_1}^2}{4}+Z_1 Z_2}=\frac{{Z_{1}^{\'}}\cancel{^2}{Z_{2}^{\'}}^2}{\frac{{Z_{1}^{\'}}\cancel{^2}}{4}+\cancel{Z_{1}^{\'}}Z_{2}^{\'}}\\<br />&=&\frac{{Z_{1}^{\'}}{Z_{2}^{\'}}^2}{\frac{{Z_{1}^{\'}}}{4}+Z_{2}^{\'}}<br />\end{eqnarray}

という関係が成り立つ。Z2'の関係式を代入してZ1'について解くと

\begin{eqnarray}<br />Z_{1}^{\'}&=&\frac{{Z_1}^2{Z_2}^2{Z_{2}^{\'}}}{{Z_{2}^{\'}}^2\left(\frac{{Z_1}^2}{4}+Z_1 Z_2\right)-\frac{{Z_1}^2{Z_2}^2}{4}}\\<br />&=&\frac{1}{{Z_{2}^{\'}}\cancel{^2}\left(\frac{\cancel{{Z_1}^2}}{4\cancel{{Z_1}^2}{Z_2}^2\cancel{Z_{2}^{\'}}}+\frac{\cancel{Z_1 Z_2}}{{Z_1}\cancel{^2}{Z_2}\cancel{^2}\cancel{Z_{2}^{\'}}}\right)-\frac{\cancel{{Z_1}^2{Z_2}^2}}{4\cancel{{Z_1}^2{Z_2}^2}{Z_{2}^{\'}}}}\\<br />&=&\frac{1}{\frac{\cancel{Z_{2}}}{m}\left(\frac{1}{4{Z_2}\cancel{^2}}+\frac{1}{{Z_1}\cancel{Z_2}}\right)-\frac{1}{4 \frac{Z_{2}}{m}}}=\frac{1}{\frac{1}{4 m{Z_2}}+\frac{1}{m{Z_1}}-\frac{m}{4 Z_{2}}}\\<br />&=&\frac{1}{\frac{1}{m Z_1}+\frac{1-m^2}{4 m Z_{2}}}\\<br />&=&\frac{1}{\frac{1}{m Z_1}+\frac{1}{\frac{4 m}{1-m^2}Z_2}}<br />\end{eqnarray}

ということになる。これを回路に反映すると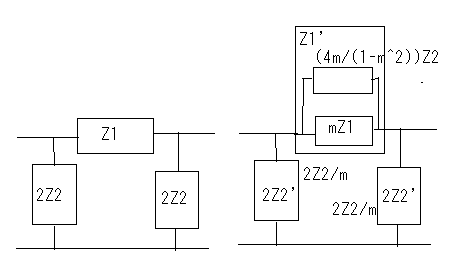



ということになる。

m=1とするとTおよびπどちらの形でも元の定K形フィルタと同じ回路になることから、定K形フィルタが誘導m形フィルタの一種にも思える。元々定K形フィルタから派生した誘導m形フィルタ回路なのに、それ自身のバリエーションの一つに元の定K形フィルタ回路も包含されるというのは数学的にも面白い。

これで誘導m形の回路構成を得ることができたので、次は目標としていた遮断周波数付近の減衰を定K形よりも急峻にできるのかどうか確かめるために減衰特性を調べることになる。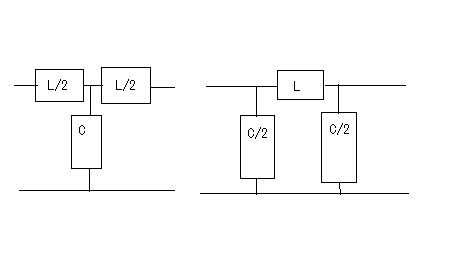



最初に上の定K形フィルタから導出した以下の誘導m形フィルタ回路を調べることにしよう。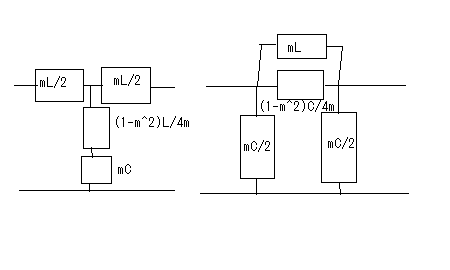



上の誘導m形フィルタの回路を見ながら、特定の周波数で無限大の減衰が得られるだろうか自問自答してみよう。右のT字回路ではLC直列回路の共振点で回路は短絡され負荷をバイパスすることになるので無限大の減衰が得られる。この共振点は無限大の減衰を与えるのでω∞とすると、

\begin{eqnarray}<br />\omega_{\infty}&=&\frac{1}{\sqrt{\left(\frac{1-m^2}{4m}L\right)\left(m C\right)}}\\<br />&=&\frac{\omega_0}{\sqrt{1-m^2}}\\<br />\omega_0&=&\frac{2}{\sqrt{L C}}<br />\end{eqnarray}

ということになる。ω0は元の定K形フィルタ回路の遮断周波数であることは今まで学んだ通り。

同様にして右のπ形回路に関してもシリーズのLC並列回路の反共振点でインピーダンスが無限大になり出力に電流が一切流れなくなるため無限大の減衰を与えることになる。

今度は元になっている定K形回路のZ1とZ2をパラメータとして変化させて減衰特性を解析してみよう。

定K形フィルタと同様に今度は導出されたインピーダンスZ1',Z2'によってパラメータx'を以下のように定めると

\begin{eqnarray}<br />{x^{\'}}^2&=&\frac{-Z_{1}^{\'}}{4 Z_{2}^{\'}}=\frac{-m Z_1}{4\left[\frac{1-m^2}{4m}Z_1+\frac{Z_2}{m}\right]}\\<br />&=&\frac{-m^2}{1-m^2+4\frac{Z_2}{Z_1}}\\<br />&=&\frac{m^2}{-\left(1-m^2\right)+\frac{1}{x^2}}\\<br />x^2&=&\frac{-Z_1}{4 Z_2}<br />\end{eqnarray}

ということになる。ここでxは元の定K形フィルタのパラメータである。従って、

\begin{eqnarray}<br />x^2&=&\frac{1}{1-m^2}<br />\end{eqnarray}

が成り立つ場合にx'が無限大の値を取り、減衰量(cosh^-1 x')が無限大となる。無限大の減衰量を与えるxをx∞と置くと、

\begin{eqnarray}<br />x_{\infty}^2&=&\frac{1}{1-m^2}<br />\end{eqnarray}

これを用いて先のx'の式を書き換えると

\begin{eqnarray}<br />{x^{\'}}^2&=&\frac{m^2}{-\frac{1}{x_{\infty}^2}+\frac{1}{x^2}}<br />\end{eqnarray}

ということになる。ここで上記の式は、xが定K形フィルタに関連した正規化周波数、x'が誘導m形フィルタに関する正規化周波数とするxに関する関数で、x∞がx'を無限大にするxの値、mが誘導m形フィルタ回路の定数である。この関数をxがx∞未満の時、それからx'^2が負の時、xがx∞より大きくx'^2が正の時に関して評価する。これら３つの条件に通過域、減衰域、それに減衰量の式を関係づけるために、定K形フィルタの時のように表で要約する。

\begin{eqnarray}<br />\begin{array}Sign\, of & Limits\, of & Type\, of & Attenation & Phase\, shift\\<br />{x^{\'}^2} & x^2 & band & & \theta \\<br />positive & 0\le x^2 \le 1 & pass & \alpha=0 & \beta=2\,sin^{-1}\,x^{\'}\\<br />positive & 1\le x^2\le {x_{\infty}}^2 & stop & \alpha=2\,cosh^{-1}\,x^{\'} & \pm\pi\\<br />negative & {x_{\infty}}^2\le x^2\le\infty & stop & \alpha=2\,sinh^{-1}\,\sqrt{\frac{Z_{1}^{\'}}{4 Z_{2}^{\'}}}=2\,sinh^{-1}\,j\,x^{\'} & 0\end{array}<br />\end{eqnarray}

またしてもValkenburgの著書に誤植を発見。x^2の範囲でx∞とあるのはx∞^2でなければならないはず。（2011/6/5 それとx'^2が正のケースでのαの式が不適切だったので、定K形フィルタの時の解析結果に立ち戻って正しい形に書き直した。)

以下のx∞とxをパラメータとして変化させた場合の減衰量と位相量のグラフをプロットすると

\begin{eqnarray}<br />x^{\'}&=&\frac{m}{\sqrt{-\frac{1}{{x_{\infty}}^2}+\frac{1}{x^2}}}\,\,\,x_{\infty}=\frac{1}{\sqrt{1-m^2}}<br />\end{eqnarray}

m=0.6としてプロットすると、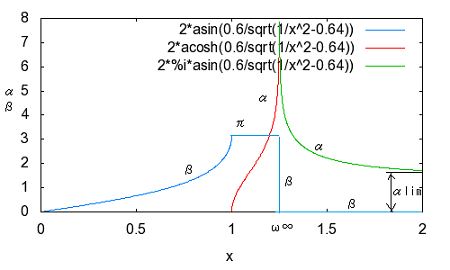



ということになる。比較するためにm=1として元の定K形フィルタ回路のそれと同様にプロットすると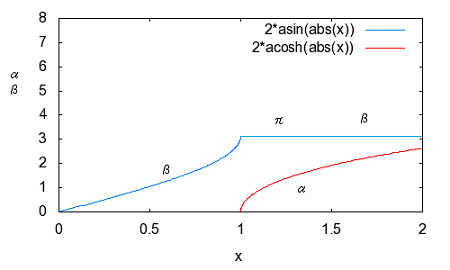



確かに比べると誘導m形フィルタでは減衰量（α）の立ち上がりが遮断周波数（通過域と減衰域の境界）に近いω∞近傍で急峻になっていることがわかる。

それ以外の点では、誘導m形の場合、xが大きくなればなるほどαminという最小値に近づくのに対して、定K形ではαは大きくなる一方である。

誘導m形フィルタと定K形フィルタはそれぞれ長所と短所があるが、同じ映像インピーダンスを持つのでそれらを組み合わせた複合フィルタを作ると互いの欠点を長所で補い合うことが可能である。

誘導m形フィルタではx=x∞で位相定数がπと0との間を変化する不連続点が現れる。またx∞以上では位相定数は0となり位相推移がまったく生じないことを意味する。

またx∞を1に限りなく近づけるほど(mを0に近づければ近づけるほど）、遮断周波数近傍の減衰が急峻となることが予想される。m=0とするとはたしてどうなってしまうのだろうか？

それとαminなる値はxがx∞以上の場合の位相定数の式から

\begin{eqnarray}<br />\alpha_{min}&=&\lim_{x\to\infty}2\,sinh^{-1}\,j\,x^{\'}=\lim_{x\to\infty}2\,sinh^{-1}j\,\frac{m}{\sqrt{-\frac{1}{{x_{\infty}}^2}+\frac{1}{x^2}}}\\<br />&=&2\,sinh^{-1}j\,\frac{m}{\sqrt{-\frac{1}{{x_{\infty}}^2}}}\\<br />&=&2\,sinh^{-1}j\,\frac{m}{\sqrt{\frac{-1}{\frac{1}{1-m^2}}}}\\<br />&=&2\,sinh^{-1}\frac{m}{\sqrt{1-m^2}}<br />\end{eqnarray}

ということになる。

あるいは複素双曲線関数の公式から

\begin{eqnarray}<br />cosh^{2}\,\frac{\alpha_{min}}{2}&=&1+sinh^{2}\,\frac{\alpha_{min}}{2}=1+\frac{m^2}{1-m^2}=\frac{1}{1-m^2}\\<br />tanh\,\frac{\alpha_{min}}{2}&=&\frac{sinh\,\frac{\alpha_{min}}{2}}{cosh\,\frac{\alpha_{min}}{2}}=\frac{\frac{m}{\cancel{\sqrt{1-m^2}}}}{\frac{1}{\cancel{\sqrt{1-m^2}}}}=m\\<br />\alpha_{min}&=&2\,tanh^{-1}\,m<br />\end{eqnarray}

ということになる。

最後の式からmが0に近づくにつれαminもまた0に近づくことになる。大小２つのmに関してαをプロットして比較してみると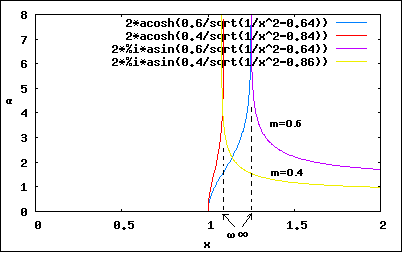



mが小さくなるαminも小さくなっていき、m=0では0となることもわかる。つまりあまりmを0に近づけても遮断周波数近傍の減衰域は急峻になるものの、それ以外の減衰域ではほとんど減衰しないという都合の悪いものになってしまう。

従って対称T字形フィルタや対称π形フィルタで構成される誘導m形フィルタの場合で取り得るmの値の範囲は

\begin{eqnarray}<br />0\,\lt\,m\,\lt\,1<br />\end{eqnarray}

ということになる。

（この制限はラダー回路フィルタのみにあてはまる。1よりも大きなmは線形位相特性を持つ格子形回路に使用される。）

Zobelの誘導m形フィルタに関する特許明細文書を読むと、確かに導出に関してはValkenburgが記述しているのとあっている。ただその後の性能評価に関するValkenburgの議論はZobelの特許が映像インピーダンスを直接評価している点と大きく異なるため独自の解釈法に基づくものと思われる。特許の文章では数式を除いては一貫して大文字のMが用いられていることも驚きだ。

Zobel, O J, Electrical wave filters, U.S. Patent 1,850,146, pp. 2–3, filed 25 Nov 1930, issued 22 Mar 1932.

申請は1930年だが公開年が1932年のスタンプがついている。Zobelは誘導m形だけでなく誘導mm'形という定K形から誘導m形を導出したのと同じ過程を誘導m形に対して適用することで得られるフィルタも一緒に申請している。誘導mm'形はあまり紹介されることはないが、誘導m形よりも更に通過域のインピーダンスがフラットだという特徴がある。そのためその半回路（逆L字形回路）を定抵抗終端とのインピーダンス整合に用いることができる。同じ過程を更に繰り返すことも可能だが、素子数が増えるだけでほとんど変わらないためこの特徴のある２つだけ申請したと思われる。後に誘導m形回路の半回路についても有用な特性があるので最後に紹介しよう。

誘導m形半回路(もしくはL)の映像インピーダンス

これまで登場した対称T字形フィルタや対称π形フィルタはいずれもその元となる定K形フィルタと同じ映像インピーダンスを持ったものだった。それらを２つの半回路に分割した場合、意外な映像インピーダンス特性を持つことが発見された。これはあくまでおまけの効果で、元々の誘導m形フィルタに求められていたものではなかったと思われる。

対称T字形フィルタや対称π字形フィルタを二分割するとそれぞれ異なる非対称L字形回路となる。これは定K形フィルタでは同一のL字形回路が現れるのとは対照的である。このため半回路の映像インピーダンスは定K形フィルタの場合とは異なってくる。定K形フィルタの場合は対称T字回路の映像インピーダンスと対称π形回路の映像インピーダンスを持っていたが、誘導m形フィルタの場合は、２つの映像インピーダンスの片方は定Kフィルタと同じZiTかZiπになるが、もう片方はそれとはまったくユニークなものになる。回路図で表すと、



ということになる。

ここでZiTmは

\begin{eqnarray}<br />F&=&\left[\begin{array}1 & 0\\ \frac{1}{\frac{1-m^2}{2 m}Z_1+\frac{2}{m}Z_2} & 1\end{array}\right]\left[\begin{array}1 & \frac{m}{2}Z_1\\ 0 & 1\end{array}\right]=\left[\begin{array}1 & \frac{m}{2}Z_1\\ \frac{2\,m}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\end{array}\right]\\<br />F_i&=&\left[\begin{array}\frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{m}{2}Z_1\\ \frac{2\,m}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & 1\end{array}\right]\\<br />F_{Tm}&=&F F_i=\left[\begin{array}1 & \frac{m}{2}Z_1\\ \frac{2\,m}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\end{array}\right]\left[\begin{array}\frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{m}{2}Z_1\\ \frac{2\,m}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & 1\end{array}\right]\\<br />&=&\begin{bmatrix}\frac{4\,Z_2+\left(1+{m}^{2}\right)\,Z_1}{4\,Z_2+\left(1-{m}^{2}\right)\,Z_1} & m\,Z_1\cr \frac{4\,m\,\left( 4\,Z_2+Z_1\right) }{{\left( 4\,Z_2+\left(1-{m}^{2}\right)\,Z_1\right) }^{2}} & \frac{4\,Z_2+\left(1+{m}^{2}\right)\,Z_1}{4\,Z_2+\left(1-{m}^{2}\right)\,Z_1}\end{bmatrix}\\<br />Z_{iTm}&=&\sqrt{\frac{B}{C}}=\sqrt{\frac{\cancel{m}\,Z_1{\left( 4\,Z_2+\left(1-{m}^{2}\right)\,Z_1\right) }^{2}}{4\,\cancel{m}\,\left( 4\,Z_2+Z_1\right)}}=\sqrt{\frac{\cancel{4^2}\,Z_1 {Z_2}\cancel{^2}{\left( 1+\left(1-{m}^{2}\right)\,\frac{Z_1}{4 Z_2}\right) }^{2}}{\cancel{4^2}\,\cancel{Z_2}\left(1+\frac{Z_1}{4 Z_2}\right)}}\\<br />&=&\left( 1+\left(1-{m}^{2}\right)\,\frac{Z_1}{4 Z_2}\right)\sqrt{\frac{Z_1 {Z_2}}{1+\frac{Z_1}{4 Z_2}}}\\<br />&=&R\frac{\left(1-\left(1-m^2\right)x^2\right)}{\sqrt{1-x^2}}\\<br />R^2&=&Z_1 Z_2\\<br />x^2&=&\frac{-Z_1}{4 Z_2}<br />\end{eqnarray}

ということになる。

同様にZiπmは

\begin{eqnarray}<br />F&=&\begin{bmatrix}1 & \frac{1}{\frac{1-{m}^{2}}{2\,m\,Z_2}+\frac{m}{2\,Z_1}}\cr 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0\cr \frac{m}{2\,Z_2} & 1\end{bmatrix}=\begin{bmatrix}\frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{2\,m\,Z_1\,Z_2}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\cr \frac{m}{2\,Z_2} & 1\end{bmatrix}\\<br />F_i&=&\begin{bmatrix}1 & \frac{2\,m\,Z_1\,Z_2}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\cr \frac{m}{2\,Z_2} & \frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\end{bmatrix}\\<br />F_{i\pi m}&=&F F_i=\begin{bmatrix}\frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1} & \frac{2\,m\,Z_1\,Z_2}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\cr \frac{m}{2\,Z_2} & 1\end{bmatrix}\begin{bmatrix}1 & \frac{2\,m\,Z_1\,Z_2}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\cr \frac{m}{2\,Z_2} & \frac{4\,Z_2+Z_1}{4\,Z_2+\left( 1-{m}^{2}\right) \,Z_1}\end{bmatrix}\\<br />&=&\begin{bmatrix}\frac{4\,Z_2+\left(1+{m}^{2}\right)\,Z_1}{4\,Z_2+\left(1-{m}^{2}\right)\,Z_1} & \frac{4\,m\,Z_1\,Z_2\,\left( 4\,Z_2+Z_1\right) }{{\left( 4\,Z_2+\left(1-{m}^{2}\right)\,Z_1\right) }^{2}}\cr \frac{m}{Z_2} & \frac{4\,Z_2+\left(1+{m}^{2}\right)\,Z_1}{4\,Z_2+\left(1-{m}^{2}\right)\,Z_1}\end{bmatrix}\\<br />Z_{i\pi m}&=&\sqrt{\frac{B}{C}}=\sqrt{\frac{4\,\cancel{m}\,Z_1\,{Z_2}^2\,\left( 4\,Z_2+Z_1\right) }{{\cancel{m}\left( 4\,Z_2+\left(1-{m}^{2}\right)\,Z_1\right) }^{2}}}=\frac{2\,\sqrt{Z_1}\,{Z_2}\,\sqrt{4\,Z_2+Z_1}}{\left( 4\,Z_2+\left(1-{m}^{2}\right)\,Z_1\right)}\\<br />&=&\frac{\sqrt{Z_1\, Z_2}\sqrt{1+\frac{{Z_1}}{4\,Z_2}}}{\left( 1+\left(1-{m}^{2}\right)\,\frac{Z_1}{4\,Z_2}\right)}\\<br />&=&R\frac{\sqrt{1-x^2}}{\left(1-\left(1-m^2\right)x^2\right)}\\<br />R^2&=&Z_1 Z_2\\<br />x^2&=&\frac{-Z_1}{4 Z_2}<br />\end{eqnarray}

ということになる。

それぞれの映像インピーダンスをいくつかmを変えてxに関してプロットしてみると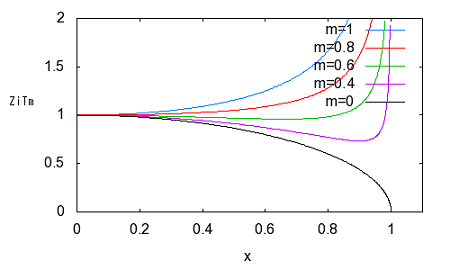



同じ表側の映像インピーダンスZiTを持つ定K形フィルタ(m=1の場合）と比べると、m=0.6の誘導M形フィルタの半回路である逆L字形フィルタの裏側の映像インピーダンスは通過域でフラットなインピーダンス特性を示している。これはこの回路を定K形フィルタや誘導M形フィルタを組み合わせた複合フィルターの両端に使用すると定抵抗Rで終端した場合でも通過域でインピーダンス不整合が最小で済むという長所を持つ。

同様に対称π形フィルタの半回路についてもプロットしてみると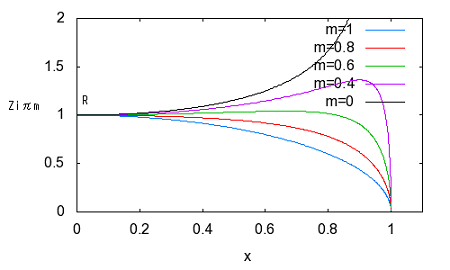



やはり同様にm=0.6の時が通過域での映像インピーダンスがフラットな特性となっている。

このことから定K形フィルタの利点（xが∞に極を持つ）と欠点（遮断周波数近辺の減衰の立ち上がりが緩やか）と誘導M形フィルタの利点（遮断周波数付近の減衰の立ち上がりが急峻）と欠点（xが∞に近づくにつれ減衰定数がαminに近づく）は２つのフィルタを組み合わせることで補完し合うが、通過域での映像インピーダンスがフラットではないため、どちらかの半回路を両端に接続することによって通過域での映像インピーダンスをフラットにすることができる。定K形フィルタおよび誘導M形フィルタの対称T字形回路と対称π形回路、およびそれらの半回路を組み合わせたラダー回路として古典フィルタが設計されたことが納得がいく。

電気回路理論でのフィルタ理論はここまでだが、Valkenburgの議論はこの後、複合フィルタ回路(composite filter)の設計法の議論に入って行く。

P.S

日本では何故にいつ頃から誘導M形フィルタと呼ばれるようになったのか謎が解けていないが、誘導M形フィルタで検索するといくつかの学校では"誘導M形変換"として教えているところもあるらしい。これは興味深い。というのも、元々定K形フィルタ回路にmをまぶして変換したものが誘導M形フィルタ回路であるわけなので、なんらかの変換操作ととらえることが自然である。

ところで誘導というと電気回路理論ではInductionとかで既に広く使われているのでderivedの訳としては適切ではないと思うのだが、数学の世界では誘導とあるのはinducedの対訳として存在する。derivedというのは既に挙げた通りderived functionという古い用語の他に新しくはDerived Algebraic Geometryというものがある。どんなものか知りたいがとても敷居が高そうなのでまたの機会にする。

単純に考えても定K形フィルタから誘導M形フィルタへの変換は線形変換では表せない。ならばどう表現するのか。またその逆の変換はあるのか、とか興味は尽きない。映像伝達関数を多変数関数として解析するあたりは、これからもいろいろな機会で役立つと思うのだが、すでに教えられる機会が無くなってしまったのは残念だ。整理された結論の式だけを追ってもおそらく表層的な理解にとどまるか、数年で忘れてしまうだろう。しかし数学的な解析手法は一生忘れることはない。今回定K形フィルタから誘導M形フィルタを導出するプロセスを知ることによって、それが後に別の様々なシーンで役立ちそうな予感がし、おそらく一生忘れることはないと思われる。最終的な映像インピーダンスの式を忘れても、自分でまた導出する方法は忘れないからである。

P.S

Zobelをはじめどの本にもmは正の実数であることを前提とした議論にとどまっている。ふと、mを複素数の範囲に拡張したらどうなるのだろうか。そう考えた時、一瞬だけ先人を超えたような気分になれる。単純にmが準虚数をとると、リアクタンスは正か負の抵抗に変わるが。しかし映像パラメータは変わらない。半世紀前はこうした議論は無意味だったかもしれない。しかし負性抵抗が理想ジャイレーターや理想オペアンプで実現できることがわかっている現代では新たな意味を持つのではないだろうか。mが複素数だとZ1'やZ2'はインピーダンスになるがZ1,Z2が誘導性か容量性かによって正負性抵抗を伴うインピーダンスとなる。これはちょっと素子数が増えるので使い勝手は悪いかもしれない。しかし解析すれば、予想もしない特徴が見いだせるかもしれない。そうした解析の楽しみは読者の課題として残して置くことにしよう（´∀｀　）
フラット表示 前のトピック | 次のトピック

題名 投稿者 日時
   フィルタ webadm 2011-5-3 7:21
     概説 webadm 2011-5-4 9:24
     定K形フィルタ webadm 2011-5-24 5:11
   » 誘導M形フィルタ webadm 2011-6-1 5:49
     複合フィルタ(composite filter) webadm 2011-6-10 5:50
     抵抗減衰器 webadm 2011-7-18 1:22

投稿するにはまず登録を
 
ページ変換(Google Translation)
EQPlayers
Allakhazam
EQresource VoA Home
Googleish(EN)
Googlean(KO)
Googlchinese(ZH-CN)
Googltwinese(ZH-TW)
Googlussian(RU)
Googlench(FR)
Googlerman(DE)
Googlabic(AR)
Googlindi(HI)
Googluguese(PT)
Googlutch(NL)
Googltarian(IT)
Googlpanish(ES)
Googlinnish(FJ)
Googlwedish(SY)
Googlatian(HR)
Googlzech(CS)
Googlgarian(BG)
Googlpolish(PL)
Googlmanian(RO)
Googlwegian(NO)
Googleek(EL)
Googldanish(DA)
サイト内検索

高度な検索