| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2013-2-15 8:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
Re: 基礎方程式とその解 表題のスレッドの続きで
と距離xに関してだけ解ける。 演算子法や作用素方程式の優れた点は、解の最終形が巨視的に見通せる点である。 両辺に波の移動速度であるcの二乗を乗じると、ポテンシャルエネルギー方程式となる。つまり送電端から受電端方向に伝達される線路上のエネルギー量を表すことになる。e=mc^2の左右を逆にしたような感じである。 とするとポテンシャルベクトルK1は初期エネルギー量で、K0は線路上のエネルギー移動量であることがすぐわかる。 そんなことを考えていると、もうひとつの見方が有ることに気づく。 進行波と反射波を、高速道路の登り下りの車線を移動する自動車の列と考えると、各自動車はなんらかのエネルギーを持っていることになる。反射波がなければ、エネルギーが速度cで線路上を浸透していく、送信端から線路に供給されるエネルギーは時間と共に増加する。 面倒なので最初は反射を考えなくて済む無限長線路で考えたが、反射があるとすると、逆方向からエネルギーの一部もしくは全部が戻ってくることになる。無損失線路でない場合には更に線路上でエネルギーは放射されて失われるので、距離と共に減衰していく。 なのでかなり一般形を考えるとややこしいことになるのがわかる。 さて次は時間に関して解く必要がある。これが難題だ。 まず以下の変換を行う どうすんだこっから(´Д`;) かなりお手上げの状態なので、Heavisideのもうひとつの著書である"ELECTROMAGNETIC THEORY"の三部作のうち演算子法について解説しているVol IIを読んでみた。 前半はありとあらゆる集中定数回路への演算子法による微分方程式の解法、それに続いて分布定数回路のあらゆる初期条件や境界条件に関する偏微分方程式の解法への応用が述べられているが、ほとんど継ぎ目なしで解説されているので、大変読むのに苦労する。知りたいのは分布定数回路のあたりだが、そこに使われている記号とかが、ずっとそれ以前のところで定義されているものだったりするので、結局遡って読む必要がある。 しかしHeavisideといえども分布定数回路の偏微分方程式に関しては距離に関して解いて時間に関しては微分演算子が残ったままの作用素方程式の状態の解について様々な初期条件を考察している。時間領域に関して解くのは後半で行われていた。 Heavisideは時間領域に関して解く段階で、どうしても解の中に任意の関数が現れてきてしまうので、独自に2つの無限べき級数で表していたが、途中からもっと良く知られている2種のBessel関数を使ったほうが良い判断して、Bessel関数を使った表現に書き直している。 318ページにほとんどこちらが導いたのと同じ形をした式があるのを見つけたときには目を疑った。なんだ良いところまでいってるんじゃないか( ´∀`) 1/2べき乗の文字が小さくて滲んでしまっているが、p=∂/∂tでσは、それよりずっと以前の218ページに以下のように定義されている。vは1/LCの平方根で波の伝達速度cと同値である。ページの最初の式と2番目の式を見比べるとcoshの部分で(p→ρ)としているのが良くわからない。双曲線関数の表記も今とは違っている。coshは同じだがsinhはshinという表記が使われている。Heavisideはそれらを演算子のように扱っているのでまた判りにくい。 説明のところでρ=0の場合には無歪み線路になる旨が解説されている。Rは線路の直列抵抗。Lは直列インダクタンス、Kは線路の漏洩コンダクタンス、Sは線路のキャパシタンスである。Heavisideの著書ではCはCurrentの意味で電流として用いられているので最初は戸惑うかもしれない。 こちらが導いた式とHeavisideの式を見比べると、薄々気づいていたが、ベクトルポテンシャルK0,K1はどうやら時間tの関数ベクトルと解釈すべきようだ。元々距離xで偏微分したら0になるのは定数の場合と、時間tの関数の場合が考えられるからだ。xで偏微分する場合には時間tは定数と見なすので0になってしまう。そのことを考慮に入れて引き続き解法を考えてみよう。 それにしてもHeavisideのElectromagnetic Theoryには無限べき級数がこれでもかと登場する。無限べき級数だらけといったほうが正しいかもしれない。 現代では流石にHeavisideの辿った脇の小道を好んで探る好き者はいないかもしれない。しかし、Heavisideの著書を読んでいると、まだ著者の息が感じられる。t=0でのコンデンサへ流れる電流の挙動を考察しているあたりでは、明らかに古典物理学の限界を垣間見るところまで近づいている感じがする。そこから先のミクロな考察は量子の世界を考えないと説明ができないからだ。そうした意味では、アマチュアが電磁気学や古典物理学の裾のから量子物理学の高みへゆっくり登ってくのにHeavisideの存在は励みになるかもしれない。マクロ的にはどうでもよいだろうと思うところまで執拗に見極めようとしている。 更にElectromagnetic Theoryを読み進めると396ページで複雑で難解な式が出尽くしたところで、簡単な集中定数回路をHeaviside演算子を使った作用素方程式に続いてHeavisdeの驚愕の告白が綴られているのを発見した。 Heaviside自身はこれまでの電信ケーブルの問題をElectromagnetic Theoryを執筆する22年前に取り組み始め、やがてMaxwellの自己誘導理論とW.Thomsonの海底電信ケーブルの理論がつながることに気づき、信号が有限速度で伝わること、Fourierの解が独立した解の無限級数になることを知り、10年目にしてやっと有限長線路の終端を短絡した場合と開放した場合を解析できたと人間の歩みの鈍さを告白している。その後の10年間で、全ての境界条件について、複雑なべき数の積であるが以下の392-393ページの簡潔な形にまとめることができた。おそらく間違いをしでかしているかもしれないが、もしそうであれば訂正を潔く受け入れようと述べている。 これがHeavisideが最終的に得た電信方程式の一般解である。 この後にも実際の解析例を具体的に示すために、進行波と反射波が伝送路上を進み電圧と電流がどう変化するかをグラフで図示している。これは今日でも観測が難しい伝送路上の信号伝搬の様子を19世紀の時代に計算してグラフとしてプロットしたというのは驚くべきことである。 数年で済む話しじゃないのね(´Д`;) まあこの電気回路理論おもちゃ箱も既に開始して5年になるし、あながち10年や20年というのは間違いではないような気がする。独学だと回り道とか寄り道とか迷い道も沢山あるし。 たまたま独自のやり方でHeavisideが歩んだ小道を横切った感じだが、他にもっとHeavisideが歩んで居なかった小径があるので、そちらを先に調べてみよう。 距離xと時間tに関してどちらから先に解いてもよいような気がするが、HeavisideもそしてどのLaplace変換を使った解法を載せているテキストも最初に距離に関して解いて、最後に時間に関して解いている。 逆をやったら途中どんな結果が得られるのだろうか? まず最初に二階の偏微分方程式を時間について解いてみると 時間で積分して距離xに関する任意の関数を出現させる これをVについて解くと ということになる。距離で先に解いたのと似たような感じになったが、いずれにせよ1/2べきの演算子が出てきてしまうのは避けられない。 ということで向きを逆方向に辿ってもここから先険しいのは一緒だ。 Heavisideも20年も脇目もふらずに解析した結果にしては最後は自身なさげである。演算子法で解くのは難しくは無いといいつつ、後半は置換に次ぐ置換の連続でどうにか一行の式にねじ込んだという感じが否めない。実際には無限級数の積の無限級数という複雑さは避けて通れないということも明らかに。 Telegraph equationで検索すると、今も新しい方法で電信方程式を解くというテーマが論文になっているぐらいなので古く新しい問題であることは変わりない。数値解析手法も様々試みられているが、最後は厳密解(解析解)との誤差分析をしなければならず、やはり解析的に見通しよく解くという需要がある。なので、電信方程式の過渡解を扱うのは学校では無理な感じもしないでもない。ちょっと存在を知っておく程度で、後で必要になったら勉強し直すというのが良いのかもしれない。 さて迷いの小径を更に元へ戻って、最初の基礎方程式のベクトル表記に戻り、そこでやはり積分を使ってみよう。 Uについて解くと ということになる。これはまだ変数分離型にする前の基礎方程式の段階だが、既にその後どうなるかは予想がつきそうな感じがする。双曲線関数が出てきているので。 Heavisideは距離についてだけ解いてまだ時間微分に関する演算子が残った状態で簡単な初期条件から始め、後に全ての条件について解を求めている。一般化というのは最後にまとめとして行っただけである。実用的には最初に初期条件を与えて解のバリエーションを絞り込んでいったほうが計算が易しい。 ここではHeavisideが歩んだ小径をなぞることはしないで、現代的な視点から見通しの良い方法を見いだしてみることにする。 余談だが、Heavisideの演算子法をまとめてある数学書というのがいくつか存在する。ひとつは先般紹介したCourant&Hilbertの"Methods of Mathematical Phisics Volume 2"の"TRANSIENT PROBLEMS AND HEAVISIDE CALCULUS"にあるp517から始まる"§2 The Heaviside Methods of Operators"である。この章では数学的な証明とかは参考文献としてMikusinskiの"Operational calculus"を挙げるに留めている。 微分演算子pとその逆演算子1/pが可換になるのは被作用素関数g(0)=0となる場合だけであるとしっかり書かれている。これは以前になんども触れている通り、Heavisideの演算子の被作用素関数には見えないHeavisideのステップ関数が常に乗じられていると考えれば納得する。 (2013/03/01) 共立の「数学公式改訂増補」の演算子法変換表を何気なくルーペで拡大して見ていたら、以下の変換対が最期の方にあるのを発見 最初に導いた解とそっくりじゃないか( ´∀`) 微妙に違うけど(´Д`;) やっとBessel関数とのつながりが見えてきた。 (2013/3/21) 上の式は演算子項がいくつもの積が含まれるので、単純に考えても畳み込み積分とかが幾重にも展開されるのが想像に難くない。やはりいきなり一般解を解くのは色々な準備を経ないとできないので、もっと特殊なケースを先に解いてみるのがよさそうである。 まず最初に最も簡単な無損失線路や無歪み線路について解いてみるのことにする。無損失線路や無歪み線路ではα-βの項は消失するので (2013/3/28) ベクトルポテンシャルK0,K1共にtに関する関数である可能性が考えられるため(例えば送電端に交流電圧が加えられる場合)、ここから先は初期条件を明らかにしてケースバイケースで解く必要がある。 最初に半無限長(受電端までの距離が送電端からの波が届かない程十分長い)かつ無損失線路を考えると ただしx0はx0>0で十分大きいとする。 これを代入するとベクトルポテンシャルに関する連立方程式が得られる これをベクトルポテンシャルK0,K1について解くと ということになる。 これを途中解の式に代入すると ということになる。 ここでx0を無限大に移行すると であるからして、半無限長線路の場合には第一項が消失し ということになる。 演算子方程式では常に両辺にHeavisideのステップ関数が乗じられているのでTaylorの定理により ということになる。 これは最初にグラフをプロットして予想した結果と一致している。 なんだ演算子法で解けるじゃないか( ´∀`) Heavisideは何故この方法を思いつかなかったのだろうか。 無損失線路ではR=G=0であるので、上の式は最終的な線路の電圧と電流を成分とするベクトルUに等しくなる。 半無限長の無歪み線路の場合には、更に一歩遡って特性方程式の段階から導く必要がある これを距離に関して2回積分しベクトルポテンシャルを出現させると これをUに関して解くと これに以下の初期条件を与えてベクトルポテンシャルK0,K1を解くと これを途中解に代入すると ここでx0を無限大に移行すると第一項が消失し ということになる。送電端からの距離によって元の波形の振幅が減衰していくことが確かめられた。 さてここから先が問題だ。有限長線路の場合にも解を導けるだろうか。それに受電端の終端条件が異なるケースについても同様である。ついでに線路の自己誘導を考慮していないThomsonのモデルの解を導くことができるだろうか? 最初にRC分布定数回路(Thomsonの海底ケーブルモデル)について考えてみよう。 RC分布定数回路ではL=G=0となるので、これまで導出した式では分母が0になってしまいまずいことになるので、基本に立ち返る必要がある。 基礎方程式の特性方程式に立ち戻ると ここでL=G=0と置くと ということになり、電信方程式は以下の様に熱伝導方程式となる これを距離で2回積分してベクトルポテンシャルK0,K1を出現させると これをUについて解くと ということになる。 ここで半無限線路の送信端に電圧Eを印可する初期条件 を与えてベクトルポテンシャルK0,K1に関して解くと これを途中解に代入すると これを半無限長線路のためx0を無限大に移行すると さてここで本格的に演算子qの1/2べき乗が出てきてしまった。 公式集より という変換対を利用することにする。 ということになる。 erfは誤差関数。 この結果から、線路を流れる電流が送電端からの距離の二乗に比例して減衰していくことをThomsonが指摘し海底ケーブルが役にたたない(受電端に達する前に線路電流が0に限りなく近づいてしまう)理由とした。 電流の式をC=0.12uF/mile, R=1kΩ/mileとしてプロットとしてみると 電圧の式を同じ条件でプロットとしてみると 100mileの地点の時間に対する変化を見ると電流はすぐにピークが現れた後減衰する一方なのに対して、電圧は指数関数的に増加する一方であるという顕著な違いが見られる。 (2013/3/31) 今まで使っていたMaximaのバージョンが古くて誤差関数がプロットできなかった。最新のMaximaをインストールしたところ意図した通りにプロットできるようになった。ようやくPAUL J. NAHINの"Oliver Heaviside"のpage 33の以下のグラフを見比べることができるようになった。 送信端からの距離が遠ければ遠いほど、電流が減衰し変化が緩慢になる。Thomsonはこのため線路の抵抗値を下げるための改良に努力した。 それだけでなくRC分布定数線路モデルでは拡散モデルのため信号が届く時間が距離が離れれば離れるほど遅くなるという電信には都合が悪い性質も示す結果となった。 当時はHeavisideがそこからインスパイアされたのと同様に驚くべき成果だったが、今日的にみると送電端から線路上の全ての点の間は抵抗でつながっているので、どんなに遠くでも送電端に加えられた信号は瞬時に線路上の全ての点に抵抗分圧されて現れるということを意味する(ただし信号のピークが伝わる速度だけは有限)。これは電気信号が有限の速度でしか伝わらないという今日の常識から見るとナンセンスである。あくまでも近似でしかない。 Heavisideが線路の自己誘導成分を考慮した電信方程式を提示したことによって信号が歪み無く一定の速度で受電端に伝わる条件があることが認められたのは電話の時代になってからのことであった。 さて半無限長線路についてはネタが尽きたところで有限長線路に解析に入ることにしよう。 その前に一度半無限長の一般の分布定数線路について解析しておこう。他にもGだけ抜いたものとかLだけ抜いた線路が考えられるが似たようなものなので。 最初に立ち返って これを距離で2度積分してベクトルポテンシャルK0,K1を出現させると これをUについて解くと ということになる。 以下の初期条件を与えてベクトルポテンシャルK0,K1を解くと これらを元の式に代入してx0を無限大に極限移行すると いいところまできたけど、ここからが腕の見せ所。 この結果から既に解析済みの半無限長の無損失線路、無歪み線路、RC分布線路の条件(を適用する正しい結果が得られることからこの式自身が一般性を失っていないことが確かめることができる。 どうすんだこっから(´Д`;) 上の式は以下の様に書き換えることができる (2013/4/1) 電圧の解はまだだけど、電流の解は得た。無歪み線路の条件α=βを適用すると先に解析済みの無歪み線路の解と同じ結果が得られることを確認。 E=1,R=1,G=0,C=1,L=1で電流をプロットすると 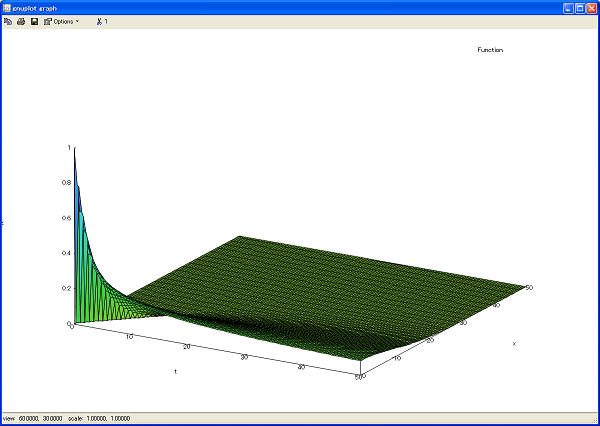 (2013/5/5) 解の導出過程に誤りがあったので修正し、再度グラフをプロットしてみたところ、やはりつまらない結果になってしまった。時間の経過とともに電流は減少し、送電端から遠い位置ほど電流も少ないという当たり前の結果である。波は空間上にも時間軸上にも現れない。 (2013/4/6) 電圧の解は一筋縄ではいかない。かなりの手数を踏まないといけなさそう。基本的に級数展開してヒントを得る必要があるのだが、級数理論を使いこなせないと難しい。それと最終的にはBessel関数が出てくるはずなので、Bessel関数についても広く深く理解しておく必要がある。電流の解からら基礎方程式に立ち戻って電圧の解を得るという方法もあるが、これはもって回った方法に思えるのでストレートとは言い難い。 上のグラフの条件だと漏洩損失こそないものの線路損失が大きいために信号が遠くに届きそうもないことが明らか。この問題が露見したのは電信から電話の時代になってからである。Heavisideは電信方程式の解からそのことを予見してその改善策を考案し特許を出願していた。それは線路の自己インダクタンスを増やせば(線路の途中に意図的に大きなインダクタンス、装荷コイルを挿入することで)同じ線路損失でも信号がより遠くまで届くというものである。 実際上のグラフの条件でLだけを2倍にしてプロットしてみると ぐんと裾のが広がって(信号が遠くまで届く)、信号が伝わる三角形のはんぺんがはっきりと見えてくる。 しかし歴史的にはHeavisideは特許から一銭も収入を得ることはなかった。主張が強すぎて特許の請求範囲を1%も譲ることをしなかったため、特許を回避する方向へ向かわせてしまったからである。 今日当たり前のように同軸ケーブルが作られ信号を忠実により遠くまで伝えるために利用されているが、それを発見したのもHeavisideである。 (2013/5/8) 依然として電圧の解に辿りつけないでいるが、ここにきて諦めもついて、やはり最初に見つけたBessel関数に関する演算子法の変換公式から出発するのがよさそうだと気づいた。共立の数学公式にたまたま古いHeavisideの演算子法が書かれていて変換表も豊富に掲載されているというのがラッキーだった。それらを最初に導いたのが誰かは出典書物が一切書かれていないという昭和初期の日本の国内事情もあってかそれ以上深追いするわけにもいかない。 最初に見つけた変換公式を両辺ともηで微分すると、指数関数の手前にある演算子関数が消える。 電圧の式ではn=0に該当するので代入すると あとは右辺を変換すればいいだけであるが、こっからが難しい。 ということになる。 実際の電圧の式では時間遅れ要素とかもあって2つの関数の積の積分を距離xで微分するということになる。面倒なのでMaximaで計算したが、何故か第一項が距離の関数になるというのは面白い。 上記の解が本当に元の電信方程式の解であるかどうかを確かめるのは読者の課題としよう( ´∀`) オリジナルのHeavisideの演算子法で電信方程式が解けるということが判っただけでも収穫である。理論はこのくらいにしていよいよ最期の演習問題にとりかかることにしよう。 P.S 読者の中には電圧の解のグラフがプロットされるものと期待されていた方もいたかもしれないが、残念ながら電流の解と違ってBessel関数を含む積分項がG=0の条件でも残るため、計算結果に虚数が現れ実空間上にはプロットできないのである。このことは電流の解でもG≠0の場合に起きたが、G=0の条件では積分項そのものが消失するので、その条件でプロットしたのだった。積分項の実数値は印可する電圧Eとして±Eの範囲内に収束することは明らかだが、Bessel関数そのものが単純な解析関数ではなく、無限べき級数という特殊な関数であるため積分計算は多大な時間を要するし、t≒x/c近辺で生じる計算誤差による虚数が積分値に加わるので積分値そのものが複素数になってしまう。これらの問題は今日もまだ未解決問題として残る。なので電信方程式の解の定式化は出来ても、その計算は未だに出来ないというのが現状である。Heavisideはどうやって19世紀にこの解をプロットしたかというのが疑問として残るが、どうやら無限べき級数が収束する項数を見極めて計算していたらしい。そうでもないと手計算では多大な時間と計算制度も対数表を使う以上、それほど有効桁数も望めないからそれはそれでよかったのである。この問題の解決も読者の自由課題としよう( ´∀`) 参考までに問題の被積分関数だけを時空間でプロットしてみたものが以下の通り 時空境界線(τ=x)近辺に裂け目が出ているのは、その領域でsqrt(tau^2-x^2)が計算誤差により純虚数になってしまい複素空間に写ってしまってプロットできないため。t=0近辺で大きな値をとるので、積分項そのものを無視するわけにもいかない。 今度は範囲外の(tau - x) < 0 もしくは (tau^2 - x^2 ) < 0の場合には関数値を強制的に0としてみたもの 依然として時空境界線付近に裂け目が現れる。複素数が計算誤差によって現れてしまっている。あとは結果が複素数なら強制的に0とするMaximaの記法があれば回避できるかもしれない。 (2013/5/15) 良く考えたら、プロットされないのは、τ-x<0の範囲で被積分関数値が複素数になるのと、τ=0で不定値になるからだった(´Д`;) そこは波が伝わっている先端部の条件だけど、そこでは値が不定になるという罠が...コンパクトじゃないのね。 (2013/5/17) よく考えたら一次のBessel関数は奇関数だった。t-(x/c)=0の場合は被積分関数は0をとると考えてよさそう(分母の式よりも分子の式の方が無限べき級数なのでt^2-(x/c)^2<1の場合早く0に近づく) 被積分関数の面に裂け目ができないようにはできたけど、積分すると状況は変わらず。もしかして積分が計算できないとかなのかな。この電圧分布の計算とプロットは読者の課題としよう( ´∀`) P.S ここしばらく開いていなかったオーム社の「大学課程 電気回路(2)」尾崎 弘著をみたら、Laplace変換を使って最終的に以下のようにまったく同じ結果が得られると書いてあった。絶版になった本の解と同じ結果が得られてもMiksinskyと吉田氏には申し訳ないが少し心許ないので、まだ絶版になってない権威が書いた本と同じ結果だと確認できて安心した。これでゆっくり眠れる。  部分的に違ってみえるのは記号の定義が異なるのと、式中の記号の数を最小化しているためで、実際はまったくの同値である。時間遅れのある単位ステップ関数u(t)を乗じることで解をケース分けして書く必要もないということである。これを見ると無歪み線路条件や無損失線路条件を適用するとそれらの既知の解と同じ結果が得られるので一般性を失っていないことを確かめることができる。完璧だ。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2012-12-18 5:18 |
| |
webadm | 2012-12-18 5:22 |
| » |
webadm | 2013-2-15 8:37 |
| 投稿するにはまず登録を | |

